Моделирование систем радиосвязи и сетей радиовещания (для студентов специальности «РРТ»)
Курс Моделирование систем радиосвязи и сетей радиовещания изучается студентами специальностей РРТ заочного обучения.
Появление большого числа квазиэлектронных и электронных систем коммуникации, характеризующихся различными структурами и алгоритмами функционирования, обусловили актуальность метода статистического или имитационного моделирования.
Целью преподавания дисциплины является изучение методов статистического моделирования систем и сетей телекоммуникаций на ЭВМ.
При моделировании на ЭВМ имитируется работа систем радиосвязи, накапливается и обрабатывается информация об имитируемом процессе. Имитационное, или статистическое моделирование на ЭВМ процессов обслуживания – универсальный и часто единственно возможный способ определения характеристик качества обслуживания.
Задачей изучения дисциплины является подготовка высококвалифицированных специалистов в области радиотехники, владеющих методами имитационного моделирования.
Для успешного усвоения этого курса необходимы знания в объеме курсов «Информатика».
Работа студентов над курсом складывается из самостоятельной работы над указанными учебниками и учебными пособиями, освоения обзорного лекционного материала, выполнения курсового проекта.
Объем курса составляет 20 часов, из них 10 час. – обзорные лекции, 4 час. –практические занятия, 6 час. – лабораторные работы на ЭВМ.
Рабочая программа курса «Моделирование систем радиосвязи и сетей радиовещания».
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
1 Введение
Цели и задачи дисциплины. Основные понятия теории моделирования систем. Использование моделирования при исследовании и проектировании сетей и систем телекоммуникаций. Основные результаты теории телетрафика. Этапы математического моделирования. Основные подходы к построению математических моделей.
2 Основы имитационного моделирования
Общая характеристика метода имитационного моделирования. Псевдослучайные последовательности. Моделирование случайных чисел, распределенных по заданному закону. Формирование моментов поступления вызовов, длительности обслуживания, случайные процессы при моделировании систем массового обслуживания (СМО) и сетей.
3 Моделирование СМО на универсальных языках программирования
Концептуальная модель СМО с отказами и ожиданием. Основные качественные показатели системы. Элементарная имитационная модель системы коммутации как модель СМО. Структурная схема модели. Модификации модели. Статистическая обработка результатов, полученных с помощью элементарной модели.
5 Планирование эксперимента и оценки точности результатов моделирование ( 2 час)
Цели планирования экспериментов с моделями систем. Стратегическое планирование имитационного эксперимента. Полный факторный эксперимент. Дробный факторный эксперимент. Частичный факторный эксперимент. Варианты построения. Тактическое планирование экспериментов с моделями систем. Оценка точности результатов моделирования. Оценка качества имитационной модели.
6 Моделирование сетей связи (6 час)
Методы коммутации в сетях связи. Теоретические модели сетей. Задание структурных параметров сетей. Основные качественные показатели функционирования сетей. Имитационная модель сети с коммутацией и обходами. Структурная схема алгоритма. Моделирование процесса маршрутизации в сетях связи.
Перечень тем практических занятий (4 час).
1 Формирование последовательности случайных чисел с заданным законом распределения. Разработка программ на универсальном языке (Паскаль, Бейсик) – 2 час.
2 Моделирование потоков вызовов, времени обслуживания вызовов – 2 час
Перечень тем лабораторных работ (2 час).
1. Разработка программ для формирования случайных чисел, распределенных по заданному закону.
2. Разработка программы элементарной СМО. Работа с программой.
Список литературы.
1. Советов Б.Я., Яковлев С.А. Моделирование систем. - М.: Высшая школа,1998г.
2. Советов Б.Я., Яковлев С.А. Моделирование систем. Практикум. - М.: Высшая школа ,1999 г.
3. Шварц М. Сети связи: Протоколы, моделирование и анализ. - М.: Наука, 1992 г.
4. Ионин Г.Л., Седол Я.Я. Статистическое моделирование систем телетрафика. – М.: 1982 г.
5. Полляк Ю.Г., Филимонов В.А. Статистическое машинное моделирование средств связи. – М.: 1988 г.
6. Шакин В.Н., Воробейчиков Л.А., Шибанов С.Е., Семенова Т.Н. Моделирование систем и сетей связи .- М.: МС ,1988г.
7. Корнышев Ю.Н., Пшеничников А.П., Харкевич А.Д. Теория телетрафика .- М.: Радио и связь, 1996.
8. Шрайбер Т.Дж. Моделирование на GPSS.- М.: Машиностроение, 1980.
9. Кудрявцев Е.М. GPSS World. Основы имитационного моделирования различных систем. – М.: ДМК Пресс, 2004.
10. Томашевский В., Жданова Е. Имитационное моделирование в среде GPSS.
- М.: Б
Методические указания к выполнению курсового проекта
Номер варианта студент определяет по первой букве своей фамилии:
А-1, Б-2, В-3, Г-4, Д-5, Ж-5, З-6, Е-7, И-8, К- 9, Л-10, М-11, Н – 12, О –13, П –14, Р – 15, С- 16, Т-17, У,Ф,Ц,Ч – 18,
Решения задач должны быть представлены алгоритмами (блок-схемами), программами на алгоритмическом языке, результатами работ программ. В случае отсутствия у студента возможности работы на ЭВМ, ему предоставляется время для работы в компьютерном классе института.
Варианты заданий
1. Разработать программу на алгоритмическом языке, реализующую алгоритм элементарной модели системы электросвязи, представленный на рис.1. Исходные данные взять из таблицы 1.
Таблица 1
Номер варианта | L1 | L2 | D1 (c) | D2 (c) | M (c) | Номер варианта | L1 | L2 | D1 (c) | D2 (c) | M (c) |
| 0 | 0,1 | 0,22 | 1,4 | 2,0 | 14,3 | 10 | 0,3 | 0,23 | 1,1 | 3,0 | 13,7 |
| 1 | 0,2 | 0,13 | 1,5 | 2,1 | 14,2 | 11 | 0,5 | 0,24 | 1,2 | 2,9 | 13,8 |
| 2 | 0,3 | 0,14 | 1,6 | 2,2 | 14,1 | 12 | 0,4 | 0,25 | 1,3 | 2,8 | 13,9 |
| 3 | 0,4 | 0,10 | 1,7 | 2,3 | 13,0 | 13 | 0,1 | 0,18 | 1,4 | 2,7 | 14,0 |
| 4 | 0,5 | 0,11 | 1,8 | 2,4 | 13,1 | 14 | 0,2 | 0,13 | 1,5 | 2,6 | 14,1 |
| 5 | 0,6 | 0,12 | 1,9 | 2,5 | 13,2 | 15 | 0,6 | 0,12 | 1,6 | 2,5 | 14,2 |
| 6 | 0,7 | 0,15 | 1,1 | 2,6 | 13,3 | 16 | 0,7 | 0,11 | 1,7 | 2,4 | 14,3 |
| 7 | 0,8 | 0,16 | 1,2 | 2,7 | 13,4 | 17 | 0,9 | 0,17 | 1,8 | 2,3 | 14,4 |
| 8 | 0,9 | 0,17 | 1,3 | 2,8 | 13,5 | 18 | 0,21 | 0,20 | 1,9 | 2,2 | 14,5 |
| 9 | 0,11 | 0,18 | 2,0 | 2,9 | 13,6 | 19 | 0,8 | 0,19 | 2,0 | 2,1 | 14,6 |
В результате работы модели получить оценки математического ожидания и среднеквадратического отклонения для следующих величин:
а) длительности пребывания обслуженного вызова в системе;
б) длительность пребывания вызова в очереди;
в) длины очереди;
г) длительности простоя линии.
При этом учесть, что
а) для 0 ![]() 5 номеров вариантов ;
5 номеров вариантов ;
б) для 6 ![]() 10 номеров вариантов ;
10 номеров вариантов ;
в) для 11 ![]() 15 номеров вариантов ;
15 номеров вариантов ;
г) для 16 ![]() 19 номеров вариантов .
19 номеров вариантов .
2. Провести испытания с программой, реализующей элементарную модель системы электросвязи.
Собрать статистические данные, вывести их в виде двух массивов X (I) и Y (I). Построить графически зависимость y=f(x). X и Y определить по таблице 3.
Таблица 3
| Номер варианта | X | Y | Номер варианта | X | Y |
| 0 | L1 |
| 10 | L2 | Рож |
| 1 | L2 |
| 11 | D2 | Рож |
| 2 | D2 |
| 12 | D1 | Рож |
| 3 | D1 |
| 13 | D1 | Ротк |
| 4 | D2 | Робс | 14 | D1 | Робс |
| 5 | М | Ротк | 15 | D2 |
|
| 6 | L1 | Рож | 16 | L1 | Робс |
| 7 | L2 | Ротк | 17 | L2 | Ротк |
| 8 | D2 | Рпреб | 18 | D1 | Рож |
| 9 | L1 | Ротк | 19 | D2 | Рпреб |
Здесь в графе Y представлены математические ожидания следующих величин:
![]() преб – длительность пребывания вызова в системе ;
преб – длительность пребывания вызова в системе ;
![]() опс – длительность ожидания в очереди;
опс – длительность ожидания в очереди;
![]() - длина очереди;
- длина очереди; ![]() прост – длительность простоя линии; Робс – вероятность обслуживания поступившего вызова, Ротк – вероятность отказа; Рож – вероятность обслуживания без ожидания; Р преб – вероятность пребывания обслуженного вызова в системе в течении времени, не превышающего заданного.
прост – длительность простоя линии; Робс – вероятность обслуживания поступившего вызова, Ротк – вероятность отказа; Рож – вероятность обслуживания без ожидания; Р преб – вероятность пребывания обслуженного вызова в системе в течении времени, не превышающего заданного.
Моделирование элементарной системы массового обслуживания
Для того чтобы получить последовательность случайных чисел с заданным законом распределения необходимо:
1 Получить равномерно- распределенные случайные числа R в интервале (0,1).
2 С помощью формул преобразования получить случайные числа с заданным законом распределения:
V = f (R).
В состав стандартных функций многих алгоритмических языков входят функции генерирования случайных чисел. Например, на языке Бейсик есть стандартная функция RND (х), генерирующая случайные числа, равномерно – распределенные в интервале (0,1).
Для каждого закона распределения есть своя формула преобразования.
Физическое описание процессов в элементарной модели сводится к следующему: в случайные моменты времени в систему поступают вызовы. Вызовы выстраиваются в очередь и обслуживаются в порядке поступления.
Предположим, что система имеет одну абсолютно надежную линию связи. Построим статистическую модель данной системы. В ней случайными величинами являются моменты поступления вызовов и время обслуживания вызовов.
Моменты времени поступления вызовов обозначим: t1, t2, . . ., tn. Эти моменты времени равны:
t1 = Z1
t2 = Z1 + Z2
t3 = Z1+Z2+Z3
.
.
.
ti = Z1+Z2+Z3+. . . + Zi
.
.
.
Zi = ti-1 – случайная величина, которая распределена по показательному закону.
Время обслуживания вызова тоже является случайной, которая подчиняется показательному закону распределения.
Введем следующие обозначения:
L1 = ![]() - интенсивность потока поступления вызовов.
- интенсивность потока поступления вызовов.
L2 = ![]() - интенсивность времени обслуживания.
- интенсивность времени обслуживания.
![]() - интервал моделирования.
- интервал моделирования.
F ( I ) – момент освобождения линии после обслуживания i-го вызова.
Т ( I ) – момент поступления i-го вызова.
Р ( I ) – длительность простоя линии перед обслуживанием i-го вызова.
W( I ) – время ожидания i-го вызова
S ( I ) - длительность обслуживания i-го вызова.
Z (I ) - длительность пребывания i-го вызова в системе.
D 1 – предельная длительность ожидания.
D2 - заданная длительность пребывания вызова в системе, обслуживание которого завершено.
С1 – счетчик поступающих вызовов.
С2 – счетчик числа вызовов в очереди.
С3 – счетчик числа вызовов, обслужат без ожидания.
С4 – счетчик числа вызовов, пребывавших в системе не более, чем заданное время.
С5 – общее число обслуженных вызовов.

Алгоритм моделирования элементарной системы представлен в виде схемы на рис.1.
Описание функционирования алгоритма.
Блок 1 : Вводим значения L1, L2, M, D1, D2 T (0)=0, F (0)=0
C1=C2=C3=C4=C5=0
Блок 2 : Формирование случайного числа V (I)
I=1, V (I) = - (1/L1) * LOG (1-R (I)), где
R (I) є ( 0,1)
R (I) – случайное число, сформированное генератором случайных чисел.
Блок 3 : T (I) = T (I-1) + V(I)
Блок 4 : Осуществляется проверка, не вышел ли момент T (I) за интервал моделирования. Вместо T (I) можно задаться количеством вызовов I.
Если условие выполняется, то переходим к блоку 21, а в противном случае к блоку 5.
Блок 5 : Подсчет числа поступивших вызовов: С1=С1+1.
Блок 6 : Подсчет текущего числа вызовов в очереди: С2=С2+1.
Блок 7 : Определяется длительность пребывания вызова в очереди:
W (I) = F (I-1)-T(1)
Блок 8 : Осуществляется проверка, ждет ли i-ый вызов в очереди или
обслуживание начинается немедленно.
Если W (I)<0, то вызов не ждал в очереди, а ждала линия.
При W (I) =0 вызов поступил точно в момент освобождения линии.
При выполнении условия управление передается блоку 9, иначе - блоку 12.
Блок 9 : Фиксируется отсутствие ожидания
W (I) =0
Блок 10 : Осуществляется подсчет числа вызовов, обслуженных без очереди:
С3=С3+1
Блок 11 : Подсчитывается длительность простое линии перед обслуживанием i-го вызова: P (I) = T (I) – F (I-1)
Блок 12 : Проверка, не превышает ли длительность ожидания вызова установленного нами предела D1.
Если условие не выполняется, то переходим к блоку 13, в противном случае – к блоку 14.
Блок 13 : По установленной дисциплине обслуживания вызов должен покинуть систему. Для этого вызова формируется предельная длительность ожидания, время обслуживания приравнивается к нулю; поскольку вызов покидает систему, то число вызовов в очереди уменьшаем на единицу.
Управление передается 21 блоку.
Блок 14 : В этом блоке формируется длительность обслуживания i-го вызова.
S (I) = - (1/L2) * LOG1(1-R(I))
R (I) є (0,1).
S(I) – случайная величина, распределенная по показательному закону.
Блок 15 : Подсчитывается момент освобождения линии после обслуживания i-го вызова:
F (I) = T (I) + W(I) + S (I)
Блок 16 : Подсчет числа вызовов в очереди:
С 2=С2-1, т.к. вызов обслужился.
Блок 17 : Подсчитывается длительность пребывания i-го вызова в системе:
Z (I) = W (I) + S (I)
Блок 18 : Проверка, не превышает ли время пребывания вызова заданной длительности D2.
Если условие выполняется, то переходим к блоку 19, если нет – к блоку 20.
Блок 19 : Подсчет числа вызовов, пребывавших в системе не более заданного времени:
С4=С4+1
Блок 20 : Определение общего числа обслуженных вызовов:
С5=С5+1.
Блок 21 : Подсчет сумм элементов массивов, необходимых для последующей статистической обработки. Этот блок не обязателен.
Управление передается блоку 2 с I=I+1.
Блок 22 : Статистическая обработка результатов.
Блок 23 : Печать результатов.
Статистическая обработка результатов моделирования
Выполняя работу программы несколько раз, т.е. экспериментируя с моделью можно собрать необходимую статистику.
В результате статистической обработки получаем оценки математических ожиданий, дисперсии и среднеквадратических отклонений следующих величин:
а) длительности пребывания обслуженного вызова в системе:
![]() преб=
преб= ![]() ; sпреб =
; sпреб = 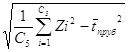 ;
;
б) длительности пребывания вызова в очереди:
![]() ож=
ож= ![]() ; sож =
; sож =  ;
;
в) длины очереди:
![]() =
= ![]() ; sL =
; sL =  ;
;
г) длительности простоя линии :
![]() ; s =
; s =  .
.
Оцениваются и другие величины:
1) Вероятность обслуживания поступившего вызова: Робсл. = С5/С1;
2) Вероятность отказа: Ротк. = 1 – С5/С1;
3) Вероятность обслуживания вызова без ожидания: Рбез ож. = С3/С1 ;
4) Вероятность пребывания обслуженного вызова в системе в течение времени, не превышающего заданного: Рпреб = С4/С1.