Интерполирование сплайнами

ИНТЕРПОЛИРОВАНИЕ СПЛАЙНАМИ.

Интерполирование многочленом Лагранжа или Ньютона на отрезке с использованием большого числа узлов интерполяции часто приводит к плохому приближению, что объясняется сильным накоплением погрешностей в процессе вычислений. Кроме того из-за расходимости процесса интерполяции увеличение числа узлов не обязано приводить к повышению точности. Для того, чтобы избежать больших погрешностей, весь отрезок разбивают на частичные отрезки и на каждом из частичных отрезков приближенно заменяют функцию многочленом невысокой степени ( так называемая кусочно-полиномиальная интерполяция).

Одним из способов интерполяции на всем отрезке является интерполирование с помощью сплайн-функций. Сплайн-функцией или сплайном называют кусочно-полиномиальную функцию, определенную на отрезке и имеющую на этом отрезке некоторое число непрерывных производных.

Слово ,,сплайн’’ (английское spline) означает гибкую линейку, используемую для проведения гладких кривых через заданные точки плоскости.

Преимущество сплайнов перед обычной интерполяцией является, во-первых, их сходимость, и, во-вторых, устойчивость процесса вычислений.

Рассмотрим частный, но распространенный в вычислительной практике случай, когда сплайн определяется с помощью многочленов третьей степени ( кубический сплайн).

Пусть на задана непрерывная функция. Введем узлы ( сетку):

и обозначим

Интерполяционным кубическим сплайном, соответствующим данной функции и данным узлам, называеться функция , удовлетворяющая следующим усовиям:

а) на кождом сегменте функция является многочленом третьей степени;

б) функция , а так же ее первая и вторая производные непрерывны на ;

в)

Последнее условие называется условием интерполирования.

Докажем существование и единственность сплайна, определяемого перечисленными условиями (плюс некоторые граничные условия, которые будут введены в процессе доказательства). Приводимое ниже доказательство содержит также способ построения сплайна.

На каждом из отрезков будем искать функцию в виде многочлена третьей степени

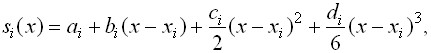(1)

где - коэффициенты, подлежащие определению. Выясним смысл введенных коэффициентов. Имеем

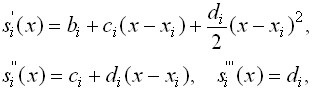
поэтому

Из условий интерполирования получаем, что

Доопределим , кроме того , .

Далее , требование непрерывности функции приводит к условиям

Отсюда,учитывая выражения для функций получаем при уравнения

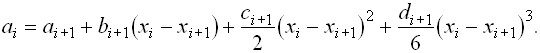Обозначая перепишем эти уравнения в виде

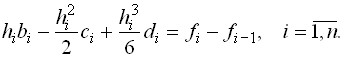(2)

Условия непрерывности первой производной

приводят к уравнениям

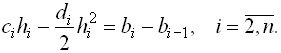(3)

Из условий непрерывности второй производной получаем уравнения

. (4)

Объединяя (2) -(4) , получим систему уравнений относительно неизвестных

Два недостающих условия получают, задавая те или иные граничные условия для Предположим, например, что функция удовлетворяет условиям Тогда естественно требовать, чтобы Отсюда получаем

т.е.

Заметим, что условие совпадает с уравнением (4) при . Таким образом, приходим к замкнутой системе уравнений для определения коэффициентов кубического сплайна:

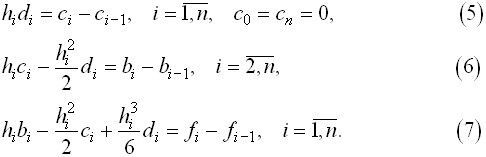Убедимся в том, что эта система имеет единственное решение. Исключим из (5)- (7) переменные и получим систему, содержащую только Для этого рассмотрим два соседних уравнения (7) :

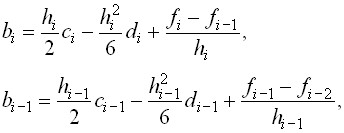
и вычтем второе уравнение из первого. Тогда получим

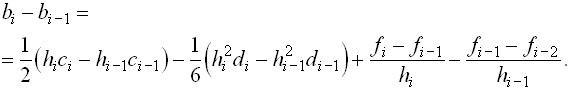
Подставляя найденное выражение для в правую часть уравнения (6), получим

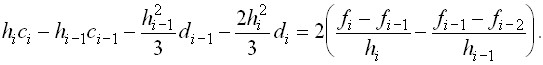(8)

Далее, из уравнения (5) получаем

И подставляя эти выражения в (8) , приходим к уравнению

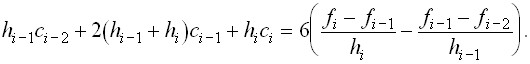
Окончательно для определения коэффициентов получаем систему уравнений

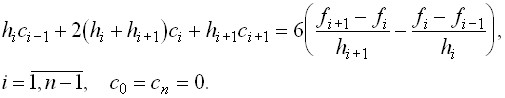(9)

В силу диагонального преобладания система (9) имеет единственное решение. Так как матрица системы трехдиагональная, решение можно найти методом прогонки. По найденным коэффициентам коэффициенты і определяются с помощь явных формул

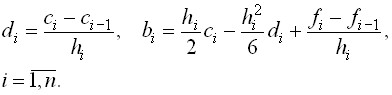(10)

Таким образом, доказано, что существует единственный кубический сплайн, определяемый условиями а)-в) и граничными условиями Заметим , что можно рассматривать и другие граничные условия.