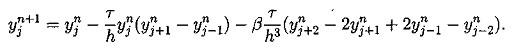Уравнение Кортевега - де Фриса, солитон, уединенная волна
Содержание
1. Введение | 3 |
1.1. Волны в природе | 3 |
1.2. Открытие уединенной волны | 4 |
1.3. Линейные и нелинейные волны | 5 |
2. Уравнение Кортевега - де Фриса | 8 |
2.1. Солитоны Кортевега - де Фриса | 10 |
2.2. Групповой солитон | 13 |
3. Постановка задачи | 15 |
3.1. Описание модели | 15 |
3.2. Постановка дифференциальной задачи. | 15 |
4. Свойства уравнения Кортевега - де Фриза | 16 |
4.1. Краткий обзор результатов по уравнению КдФ | 16 |
4.2. Законы сохранения для уравнения КдФ | 17 |
5. Разностные схемы для решения уравнения КдФ | 19 |
5.1. Обозначения и постановка разностной задачи. | 19 |
5.2. Явные разностные схемы (обзор) | 21 |
5.3 Неявные разностные схемы (обзор). | 23 |
6.Численное решение | 25 |
7. Заключение | 26 |
8. Литература | 27 |
1. Введение
Из школьного курса физики (1) хорошо известно, что если в какой-либо точке упругой среды (твердой, жидкой или газообразной) возбудить колебания, то они будут передаваться в другие места. Эта передача возбуждений обусловлена тем, что близкие участки среды связаны друг с другом. При этом колебания, возбужденные в одном месте, распространяются в пространстве с определенной скоростью. Волной принято называть процесс передачи возбуждений среды (в частности, колебательного процесса) от одной точки к другой.
Природа механизма распространения волны может быть различной. В простейшем случае связи между участками в среде могут быть обусловлены силами упругости, которые возникают из-за деформаций в среде. При этом в твердой упругой среде могут распространяться как продольные волны, при которых смещения частиц среды осуществляются в направлении распространения волны, так и поперечные волны, у которых смещения частиц перпендикулярны распространению волны. В жидкости или газе в отличие от твердых тел нет сил сопротивления сдвигу, поэтому могут распространяться только продольные волны. Хорошо известный пример продольных волн в природе — звуковые волны, которые возникают из-за упругости воздуха.
Среди волн иной природы особое место занимают электромагнитные волны, передача возбуждений у которых происходит из-за колебаний электрического и магнитного полей. Среда, в которой распространяются электромагнитные волны, как правило, оказывает существенное влияние на процесс распространения волн, однако электромагнитные волны в отличие от упругих могут распространяться даже в пустоте. Связь между различными участками в пространстве при распространении таких волн обусловлена тем, что изменение электрического поля вызывает появление магнитного поля и наоборот.
С явлениями распространения электромагнитных волн мы часто сталкиваемся в нашей повседневной жизни. К этим явлениям относятся радиоволны, применение которых в технических приложениях общеизвестно. В этой связи можно упомянуть работу радио и телевидения, которая основана на приеме радиоволн. К электромагнитным явлениям, только в другом частотном диапазоне, относится также свет, с помощью которого мы видим окружающие нас предметы.
Очень важным и интересным типом волн являются волны на поверхности воды. Это один из распространенных видов волн, который каждый наблюдал еще в детстве и который обычно демонстрируется в рамках школьного курса физики. Однако, по выражению Ричарда Фейнмана (2), "более неудачного примера для демонстрации волн придумать трудно, ибо эти волны нисколько не похожи ни на звук, ни на свет; здесь собрались все трудности, которые могут быть в волнах".
Если рассмотреть достаточно глубокий бассейн, наполненный водой, и на его поверхности создать некоторое возмущение, то по поверхности воды начнут распространяться волны. Возникновение их объясняется тем, что частицы жидкости, которые находятся вблизи впадины, при создании возмущения будут стремиться заполнить впадину, находясь под действием силы тяжести. Развитие этого явления со временем и приведет к распространению волны на воде. Частицы жидкости в такой волне двигаются не вверх-вниз, а приблизительно по окружностям, поэтому волны на воде не являются ни продольными, ни поперечными. Они как бы смесь тех и других. С глубиной радиусы окружностей, по которым двигаются частицы жидкости, уменьшаются до тех пор, пока они не станут равными нулю.
Если анализировать скорость распространения волны на воде, то оказывается, что она зависит от ее длины. Скорость длинных волн пропорциональна корню квадратному из ускорения свободного падения, умноженному на длину волны. Причиной возникновения таких волн является сила тяжести.
Для коротких волн восстанавливающая сила обусловлена силой поверхностного натяжения, и потому скорость таких волн пропорциональна корню квадратному из частного, в числителе которого стоит коэффициент поверхностного натяжения, а в знаменателе — произведение длины волны на плотность воды. Для волн средней длины волны скорость их распространения зависит от перечисленных выше параметров задачи (2). Из сказанного ясно, что волны на воде и в самом деле довольно сложное явление.
1.2. Открытие уединенной волныВолны на воде издавна привлекали к себе внимание исследователей. Это связано с тем, что они представляют собой широко известное явление в природе и, кроме того, сопровождают перемещение судов по воде.
Любопытную волну на воде наблюдал шотландский ученый Джон Скотт Рассел в 1834 году. Он занимался исследованием перемещения по каналу баржи, которую тянула пара лошадей. Неожиданно баржа остановилась, но масса воды, которую баржа привела в движение, не остановилась, а собралась у носа судна, а затем оторвалась от него. Далее эта масса воды покатилась по каналу с большой скоростью в виде уединенного возвышения, не меняя своей формы и не снижая скорости.
На протяжении всей жизни Рассел неоднократно возвращался к наблюдению за этой волной, поскольку верил, что открытая им уединенная волна играет важную роль во многих явлениях в природе. Он установил некоторые свойства этой волны. Во-первых, заметил, что она движется с постоянной скоростью и без изменения формы (3). Во-вторых, нашел зависимость скорости С этой волны от глубины канала h и высоты волны а:
![]()
где g — ускорение свободного падения, причем a < h. В-третьих, Рассел обнаружил, что возможен распад одной большой волны на несколько волн. В-четвертых, он отметил, что в экспериментах наблюдаются только волны возвышения. Однажды он также обратил внимание, что открытые им уединенные волны проходят друг через друга без каких-либо изменений, как и малые волны, образованные на поверхности воды. Однако на последнее очень важное свойство он не обратил существенного внимания.
Работа Рассела, опубликованная в 1844 году как "Доклад о волнах", вызвала осторожную реакцию в среде ученых. На континенте ее не заметили совсем, а в самой Англии на нее обратили внимание Г.Р. Эйри и Дж.Г. Стоке. Эйри подверг критике результаты экспериментов, которые наблюдал Рассел. Он отмечал, что из теории длинных волн на мелкой воде выводы Рассела не получаются, и утверждал, что длинные волны не могут сохранять неизменную форму. И в конечном итоге подверг сомнению правильность наблюдений Рассела. Один из основателей современной гидродинамики, Джордж Габриэль Стоке, также не согласился с результатами наблюдений, полученными Расселом, и критически отнесся к факту существования уединенной волны.
После столь негативного отношения к открытию уединенной волны долгое время о ней просто не вспоминали. Определенную ясность в наблюдения Рассела внесли Дж. Буссинеск (1872 год) и Дж.У. Рэлей (1876 год), которые независимо друг от друга нашли аналитическую формулу для возвышения свободной поверхности на воде в виде квадрата гиперболического секанса и вычислили скорость распространения уединенной волны на воде.
Позже опыты Рассела были повторены другими исследователями и получили подтверждение.
1.3. Линейные и нелинейные волныВ качестве математических моделей при описании распространения волн в различных средах часто используют уравнения в частных производных. Это такие уравнения, которые содержат в качестве неизвестных производные от характеристик рассматриваемого явления. Причем поскольку характеристика (например, плотность воздуха при распространении звука) зависит от расстояния до источника и от времени, то и в уравнении используются не одна, а две (а иногда и больше) производные. Простое волновое уравнение имеет вид
utt=c2uxx (1.1)
Характеристика волны и в этом уравнении зависит от пространственной координаты х и времени t, а индексы у переменной и обозначают вторую производную от и по времени (utt) и вторую производную от и по переменной x(uxx). Уравнение (1) описывает плоскую одномерную волну, аналогом которой может служить волна в струне. В этом уравнении в качестве и можно принять плотность воздуха, если речь идет, например, о звуковой волне в воздухе. Если рассматривают электромагнитные волны, то под и следует понимать напряженность электрического или магнитного поля.
Решение волнового уравнения (1), которое впервые было получено Ж. Д'Аламбером в 1748 году, имеет вид
u(x,t)=f(x-ct)+g(x+ct) (1.2)
Здесь функции f и g находят из начальных условий для и. Уравнение (1.1) содержит вторую производную от и по t, поэтому для него следует задавать два начальных условия: значение и при t = 0 и производную и, при t = 0.
Волновое уравнение (1.1) имеет очень важное свойство, суть которого заключена в следующем. Оказалось, что если взять два любых решения этого уравнения, то их сумма снова будет решением этого же уравнения. Это свойство отражает принцип суперпозиции решений уравнения (1.1) и соответствует линейности явления, которое оно описывает. Для нелинейных моделей это свойство не выполняется, что приводит к существенным отличиям протекания процессов в соответствующих моделях. В частности, из выражения для скорости уединенной волны, которую наблюдал Рассел, следует, что ее значение зависит от амплитуды, а для волны, описываемой уравнением (1.1), такой зависимости нет.
Непосредственной подстановкой в уравнение (1.1) можно убедиться, что зависимость
u(x,t)=a cos(kx-ωt) (1.3)
в которой а, k и ω — постоянные, при ω =±k является решением уравнения (1). В этом решении а — амплитуда, k — волновое число, а ω — частота. Приведенное решение представляет собой монохроматическую волну, переносимую в среде с фазовой скоростью
cp=![]() (1.4)
(1.4)
На практике монохроматическую волну создать трудно, и обычно имеют дело с цугом (пакетом) волн, в котором каждая волна распространяется со своей скоростью, а скорость распространения пакета характеризуется групповой скоростью
Cg=![]() , (1.5)
, (1.5)
определяемой через производную от частоты ω по волновому числу k.
Определить, с какой (линейной или нелинейной) моделью имеет дело исследователь, не всегда легко, но когда математическая модель сформулирована, то решение этого вопроса упрощается и выполнение принципа суперпозиции решений можно проверить.
Возвращаясь к волнам на воде, заметим, что их можно анализировать используя хорошо известные уравнения гидродинамики, о которых известно, что они нелинейны. Поэтому и волны на воде в общем случае являются нелинейными. Только в предельном случае малых амплитуд эти волны могут считаться линейными.
Отметим, что и распространение звука не во всех случаях описывается линейным уравнением. Еще Рассел при обосновании своих наблюдений по уединенной волне отметил, что звук от выстрела пушки распространяется в воздухе быстрее, чем команда произвести этот выстрел. Это объясняется тем, что распространение мощного звука описывается уже не волновым уравнением, а уравнениями газовой динамики.
- Уравнение Кортевега - де Фриса
Окончательная ясность в проблеме, которая возникла после опытов Рассела по уединенной волне, наступила после работы датских ученых Д .Д. Кортевега и Г. де Фриса, которые попытались разобраться в существе наблюдений Рассела. Обобщив метод Рэлея, эти ученые в 1895 году вывели уравнение для описания длинных волн на воде. Кортевег и де Фрис, используя уравнения гидродинамики, рассмотрели отклонение и(х,t) от положения равновесия поверхности воды при отсутствии вихрей и при постоянстве плотности воды. Сделанные ими начальные приближения были естественны. Они также предположили, что при распространении волны выполняются два условия для безразмерных параметров
ε=![]() <<1, δ=
<<1, δ=![]() (2.1)
(2.1)
Здесь а — амплитуда волны, h — глубина бассейна, в котором рассматриваются волны, l — длина волны (рис. 1).
Суть приближений состояла в том, что амплитуда рассматриваемых волн была много меньше, чем
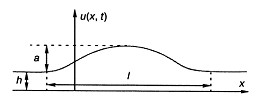
Рис. 1. Уединенная волна, распространяющаяся по каналу, и ее параметры
глубина бассейна, но в то же время длина волны была много больше, чем глубина бассейна. Таким образом, Кортевег и де Фрис рассматривали длинные волны.
Уравнение, которое было ими получено, имеет вид
ut + 6uux + uxxx = 0. (2.2)
Здесь u(x,t) - отклонение от положения равновесия поверхности воды (форма волны) - зависит от координаты x и времени t. Индексы у характеристики u означают соответствующие производные по t и по x. Это уравнение, как и (1), является уравнением в частных производных. Изучаемая характеристика у него (в данном случае u) зависит от пространственной координаты x и времени t.
Решить уравнение такого типа - значит найти зависимость u от x и t, после подстановки которой в уравнение мы придем к тождеству.
Уравнение (2.2) имеет волновое решение, известное с конца прошлого века. Оно выражается через специальную эллиптическую функцию, изученную Карлом Якоби, которая носит теперь его имя.
При некоторых условиях эллиптическая функция Якоби переходит в гиперболический секанс и решение имеет вид
u(x,t)=2k2ch-2{k(x-4k2t)+φ0}, (2.3)
где φ0— произвольная постоянная.
Решение (8) уравнения (7) является предельным случаем бесконечно большого периода волны. Именно этот предельный случай является уединенной волной, соответствующей наблюдению Рассела в 1834 году.
Решение (8) уравнения Кортевега— де Фриса является бегущей волной. Это означает, что оно зависит от координаты x и времени t через переменную ξ=x-c0t. Эта переменная характеризует положение точки координат, движущейся со скоростью волны с0, то есть она обозначает положение наблюдателя, который постоянно находится на гребне волны. Таким образом, уравнение Кортевега— де Фриса в отличие от решения Д'Аламбера (1.2) волнового решения (1.1) имеет волну, распространяющуюся лишь в одном направлении. Однако оно учитывает проявление более сложных эффектов вследствие дополнительных слагаемых uux и uxxx.
В действительности это уравнение является также приближенным, поскольку при его выводе использованы малые параметры (2.1) ε иδ. Если пренебречь влиянием этих параметров, устремляя их к нулю, мы получим одну из частей решения Д'Аламбера.
Конечно, при выводе уравнения для длинных волн на воде влияние параметров е и 6 может быть учтено более точно, но тогда получится уравнение, содержащее гораздо больше слагаемых, чем уравнение (2.2), и с производными более высокого порядка. Из сказанного следует, что решение уравнения Кортевега-де Фриса для описания волн справедливо только на определенном расстоянии от места образования волны и на определенном промежутке времени. На очень больших расстояниях нелинейные волны уже не будут описываться уравнением Кортевега-де Фриса, и для описания процесса потребуется более точная модель. Уравнение Кортевега-де Фриса в этом смысле следует рассматривать как некоторое приближение (математическую модель), соответствующее с определенной степенью точности реальному процессу распространения волн на воде.
Используя специальный подход, можно убедиться, что принцип суперпозиции решений для уравнения Кортевега-де Фриса не выполняется, и поэтому это уравнение является нелинейным и описывает нелинейные волны.
2.1. Солитоны Кортевега - де ФрисаВ настоящее время кажется странным, что открытие Рассела и его последующее подтверждение в работе Кортевега и де Фриса не получили заметного резонанса в науке. Эти работы оказались забытыми почти на 70 лет. Один из авторов уравнения, Д.Д. Кортевег, прожил долгую жизнь и был известным ученым. Но когда в 1945 году научная общественность отмечала его 100-летний юбилей, то в списке лучших публикаций работа, выполненная им с де Фрисом, даже не значилась. Составители списка сочли эту работу Кортевега не заслуживающей внимания. Только спустя еще четверть века именно эта работа стала считаться главным научным достижением Кортевега.
Однако если поразмыслить, то такое невнимание к уединенной волне Рассела становится понятным. Дело в том, что в силу своей специфичности это открытие долгое время считалось довольно частным фактом. В самом деле, в то время физический мир казался линейным и принцип суперпозиции считался одним из фундаментальных принципов большинства физических теорий. Поэтому никто из исследователей не придал открытию экзотической волны на воде серьезного значения.
Возвращение к открытию уединенной волны на воде произошло в какой-то степени случайно и вначале, казалось, не имело к нему никакого отношения. Виновником этого события стал величайший физик нашего столетия Энрико Ферми. В 1952 году Ферми попросил двух молодых физиков С. Улама и Д. Паста решить одну из нелинейных задач на ЭВМ. Они должны были рассчитать колебания 64 грузиков, связанных друг с другом пружинками, которые при отклонении от положения равновесия на Δl приобретали возвращающуюся силу, равную kΔl+a(Δl)2. Здесь k и a - постоянные коэффициенты. При этом нелинейная добавка предполагалась малой по сравнению с основной силой kΔl. Создавая начальное колебание, исследователи хотели посмотреть, как эта начальная мода будет распределяться по всем другим модам. После проведения расчетов этой задачи на ЭВМ ожидаемого результата они не получили, но обнаружили, что перекачивание энергии в две или три моды на начальном этапе расчета действительно происходит, но затем наблюдается возврат к начальному состоянию. Об этом парадоксе, связанном с возвратом начального колебания, стало известно нескольким математикам и физикам. В частности, об этой задаче узнали американские физики М. Крускал и Н. Забуски, которые решили продолжить вычислительные эксперименты с моделью, предложенной Ферми.
После расчетов и поиска аналогий эти ученые установили, что уравнение, которое использовали Ферми, Паста и Улам, при уменьшении расстояния между грузиками и при неограниченном росте их числа переходит в уравнение Кортевега—де Фриса. То есть по существу задача, предложенная Ферми, сводилась к численному решению уравнения Кортевега—де Фриса, предложенного в 1895 году для описания уединенной волны Рассела. Примерно в те же годы было показано, что для описания ионно-звуковых волн в плазме используется также уравнение Кортевега—де Фриса. Тогда стало ясно, что это уравнение встречается во многих областях физики и, следовательно, уединенная волна, которая описывается этим уравнением, является широко распространенным явлением.
Продолжая вычислительные эксперименты по моделированию распространения таких волн, Крускал и Забуски рассмотрели их столкновение. Остановимся подробнее на обсуждении этого замечательного факта. Пусть имеются две уединенные волны, описываемые уравнением Кортевега—де Фриса, которые различаются амплитудами и движутся друг за другом в одном направлении (рис. 2). Из формулы для уединенных волн (8) следует, что скорость движения таких волн тем выше, чем больше их амплитуда, а ширина пика уменьшается с ростом амплитуды. Таким образом, высокие уединенные волны движутся быстрее. Волна с большей амплитудой догонит движущуюся впереди волну с меньшей амплитудой. Далее в течение некоторого времени две волны будут двигаться вместе как единое целое, взаимодействуя между собой, а затем они разъединятся. Замечательным свойством этих-волн является то, что после своего взаимодействия форма и
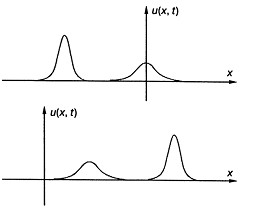
Рис. 2. Два солитона, описываемые уравнением Кортевега-де Фриса,
до взаимодействия (вверху) и после (внизу)
скорость этих волн восстанавливаются. Обе волны после столкновения лишь смещаются на некоторое расстояние по сравнению с тем, как если бы они двигались без взаимодействия.
Процесс, у которого после взаимодействия волн сохраняются форма и скорость, напоминает упругое столкновение двух частиц. Поэтому Крускал и Забуски такие уединенные волны назвали солитонами (от англ. solitary- уединенный). Это специальное название уединенных волн, созвучное электрону, протону и многим другим элементарным частицам, в настоящее время общепринято.
Уединенные волны, которые были открыты Расселом, и в самом деле ведут себя как частицы. Большая волна не проходит через малую при их взаимодействии. Когда уединенные волны соприкасаются, то большая волна замедляется и уменьшается, а волна, которая была малой, наоборот, ускоряется и подрастает. И когда малая волна дорастает до размеров большой, а большая уменьшается до размеров малой, солитоны разделяются и больший уходит вперед. Таким образом, солитоны ведут себя как упругие теннисные мячи.
Дадим определение солитона (4). Солитоном называется нелинейная уединенная волна, которая сохраняет свою форму и скорость при собственном движении и столкновении с себе подобными уединенными волнами, то есть представляет собой устойчивое образование. Единственным результатом взаимодействия солитонов может быть некоторый сдвиг фаз.
Открытия, связанные с уравнением Кортевега - де Фриса, не закончились открытием солитона. Следующим важным шагом, имеющим отношение к этому замечательному уравнению, было создание нового метода решения нелинейных уравнений в частных производных. Хорошо известно, что найти решения нелинейных уравнений очень сложно. До 60-х годов нашего столетия считалось, что такие уравнения могут иметь только некоторые частные решения, удовлетворяющие специально заданным начальным условиям. Однако уравнение Кортевега—де Фриса и в этом случае оказалось в исключительном положении.
В 1967 году американские физики К.С. Гарднер, Дж.М. Грин, М. Крускал и Р. Миура показали, что решение уравнения Кортевега—де Фриса может быть в принципе получено для всех начальных условий, которые определенным образом обращаются в нуль при стремлении координаты к бесконечности. Они использовали преобразование уравнения Кортевега - де Фриса к системе двух уравнений, называемой теперь парой Лакса (по имени американского математика Питера Лакса, внесшего большой вклад в развитие теории солитонов), и открыли новый метод решения ряда очень важных нелинейных уравнений в частных производных. Этот метод получил название метода обратной задачи рассеяния, поскольку в нем существенно используется решение задачи квантовой механики о восстановлении потенциала по данным рассеяния.
2.2. Групповой солитонВыше мы говорили, что на практике волны, как правило, распространяются группами. Подобные группы волн на воде люди наблюдали с незапамятных времен. На вопрос о том, почему для волн на воде так типичны "стаи" волн, удалось ответить Т. Бенжамену и Дж. Фейеру только в 1967 году. Теоретическими расчетами они показали, что простая периодическая волна на глубокой воде неустойчива (теперь это явление называется неустойчивостью Бенжамена—Фейера), и поэтому волны на воде из-за неустойчивости разбиваются на группы. Уравнение, с помощью которого описывается распространение групп волн на воде, было получено В.Е. Захаровым в 1968 году. К тому времени это уравнение уже было известно в физике и носило название нелинейного уравнения Шрёдингера. В 1971 году В.Е. Захаров и А.Б. Шабат показали, что это нелинейное уравнение имеет решения также в виде солитонов, более того, нелинейное уравнение Шрёдингера, так же как и уравнение Кортевега—де Фриса, может быть проинтегрировано методом обратной задачи рассеяния. Солитоны нелинейного уравнения Шрёдингера отличаются от обсуждаемых выше солитонов Кортевега—де Фриса тем, что они соответствуют форме огибающей группы волн. Внешне они напоминают модулированные радиоволны. Эти солитоны называются групповыми солитонами, а иногда солитонами огибающей. Это название отражает сохраняемость при взаимодействии огибающей волнового пакета (аналог штриховой линии, представленной на рис. 3), хотя сами волны под огибающей двигаются со скоростью, отличной от групповой. При этом форма огибающей описывается
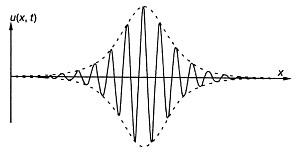
Рис. 3. Пример группового солитона (штриховая линия)
зависимостью
a(x,t)=a0 ch-1(![]() )
)
где аа - амплитуда, а l— половина размера солитона. Обычно под огибающей солитона находится от 14 до 20 волн, причем средняя волна самая большая. С этим связан хорошо известный факт, что самая высокая волна в группе на воде находится между седьмой и десятой (девятый вал). Если в группе волн образовалось большее количество волн, то произойдет ее распад на несколько групп.
Нелинейное уравнение Шрёдингера, как и уравнение Кортевега— де Фриса, также имеет широкую распространенность при описании волн в различных областях физики. Это уравнение было предложено в 1926 году выдающимся австрийским физиком Э. Шрёдингером для анализа фундаментальных свойств квантовых систем (4) и первоначально использовано при описании взаимодействия внутриатомных частиц. Обобщенное или нелинейное уравнение Шрёдингера описывает совокупность явлений в физике волновых процессов. Например, оно используется для описания эффекта самофокусировки при воздействии мощного лазерного луча на нелинейную диэлектрическую среду и для описания распространения нелинейных волн в плазме.
3. Постановка задачи
3.1. Описание модели. В настоящее время наблюдается значительно возрастающий интерес к исследованию нелинейных волновых процессов в различных областях физики (например, в оптике, физике плазмы, радиофизике, гидродинамике и т.д.). Для изучения волн малой, но конечной амплитуды в дисперсионных средах в качестве модельного уравнения часто используют уравнение Кортевега-де Фриза (КдФ):
ut + иих + βиххх = 0 (3.1)
Уравнение КдФ было использовано для описания магнитозвуковых волн, распространяющихся строго поперек магнитного поля или под углами, близкими к ![]() .
.
Основные предположения, которые делаются при выводе уравнения: 1) малая, но конечная амплитуда, 2) длина волны велика по сравнению с длиной дисперсии.
Компенсируя действие нелинейности, дисперсия дает возможность формироваться в дисперсионной среде стационарным волнам конечной амплитуды - уединенным и периодическим. Уединенные волны для уравнения КдФ после работы (8) стали называться солитонами (9). Периодические волны носят название кноидальных волн. Соответствующие формулы для их описания даны в (4).
3.2. Постановка дифференциальной задачи. В работе исследуется численное решение задачи Коши для уравнения Кортевега-де Фриза с периодическими условиями по пространству в прямоугольнике QT={(t,x):0 ut + иих + βиххх = 0 (3.2) u(x,t)|x=0=u(x,t)|x=l (3.3) с начальным условием u(x,t)|t=0=u0(x) (3.4) 4. Свойства уравнения Кортевега - де Фриза 4.1. Краткий обзор результатов по уравнению КдФ. Задача Коши для уравнения КдФ при различных предположениях относительно u0(х) рассматривалась во многих работах (10-17). Задача о существовании и единственности решения с условиями периодичности в качестве краевых условий была решена в работе (10) с помощью метода конечных разностей. Позже, при менее сильных предположениях, существование и единственность были доказана в статье (11) в пространстве L∞(0,T,Hs(R1)), где s>3/2, а в случае периодической задачи - в пространстве L∞(0,T,H∞(C))где С - окружность длины, равной периоду, на русском языке эти результаты представлены в книге (12). Случай, когда не предполагается какая-либо гладкость начальной функции u0∈L2(R1), рассмотрен в работе (13). Там вводится понятие обобщенного решения задачи (3.2),(3.4), устанавливается существование обобщенного решения и(t,х) ∈ L∞(0,T,L2(R1)) в случае произвольной начальной функции u0 ∈L2(R1); при этом и(t,х) ∈ L2(0,Т;H-1(-r,r)) для любого r>0, и если для некоторого α > 0 (xαu02(x)) ∈ L1(0,+∞) , то Используя обращение линейной части уравнения при помощи фундаментального решения G(t,x) соответствующего линейного оператора Задача Коши для уравнения КдФ исследовалась также методом обратной задачи рассеяния, предложенном в работе (14). При помощи этого метода были получены результаты о существовании и гладкости решений при достаточно быстро убывающих начальных функциях, причем в (15) установлен, в частности, результат о разрешимости задачи (3.2),(3.4) в пространстве C∞(О, Т; S(R1)). Наиболее полный обзор современных результатов по уравнению КдФ можно найти в (16). 4.2. Законы сохранения для уравнения КдФ. Как известно, для уравнения КдФ существует бесконечное число законов сохранения. В работе (17) приводится строгое доказательство этого факта. В работах (11), (12) различные законы сохранения применялись для доказательства нелокальных теорем существования решения задачи (3.2),(3.4) из соответствующих пространств. Продемонстрируем вывод первых трех законов сохранения для задачи Коши на R1 и периодической задачи. Для получения первого закона сохранения достаточно проинтегрировать уравнения (3.2) по пространственной переменной. Получим: отсюда и следует первый закон сохранения: Здесь в качестве a и b выступают +∞ и -∞ для задачи Коши и границы основного периода для периодической задачи. Поэтому второе и третье слагаемые обращаются в 0. Для вывода второго закона сохранения следует умножить уравнение (3.2) на 2 u(t,x) и проинтегрировать по пространственной переменной. Тогда, используя формулу интегрирования по частям получим: но в силу "краевых" условий все слагаемые кроме первого опять сокращаются Таким образом второй интегральный закон сохранения имеет вид: Для вывода третьего закона сохранения нужно умножить наше уравнение (3.2) на (и2 + 2β ихх), таким образом получим: После применения несколько раз интегрирования по частям третий и четвертый интегралы сокращаются. Второе и третье слагаемые исчезают из-за граничных условий. Таким образом из первого интеграла получаем: что эквивалентно А это и есть третий закон сохранения для уравнения (3.2). Под физическим смыслом первых двух интегральных законов сохранения в некоторых моделях можно понимать законы сохранения импульса и энергии, для третьего и последующих законов сохранения физический смысл охарактеризовать уже труднее, но с точки зрения математики эти законы дают дополнительную информацию о решении, которая используется потом для доказательств теорем существования и единственности решения, исследования его свойств и вывода априорных оценок. 5. Разностные схемы для решения уравнения КдФ 3.1. Обозначения и постановка разностной задачи. В области Введем линейное пространство Ωh сеточных функций, определенных на сетке Снабдим линейное пространство П/г нормой: Поскольку в пространство Ωh входят периодические функции, то это скалярное произведение эквивалентно скалярному произведению: Будем строить разностные схемы для уравнения (3.2) на сетке с периодическими краевыми условиями. Нам потребуются обозначения разностных аппроксимаций. Введем их. Используем стандартные обозначения для решения уравнения на очередном (n-м) временном слое, то есть Введем обозначения для разностных аппроксимаций производных. Для первой производной по времени: Аналогично для первой производной по пространству: Теперь введем обозначения для вторых производных: Третью пространственную производную будем аппроксимировать следующим образом: Также нам потребуется аппроксимация у2, которую мы обозначим буквой Q и введем следующим образом: Для записи уравнения на полу целых слоях будем использовать уравновешенную аппроксимацию, т.е. за исключением аппроксимации у2 на полу целом слое. Приведем одну из возможных аппроксимаций у2 на полу целом слое: Замечание 2. Стоит отметить, что для Определение 1. Следуя (19) разностную схему для уравнения КдФ будем называть консервативной, если для нее имеет место сеточный аналог первого интегрального закона сохранения, справедливого для дифференциальной задачи. Определение 2. Следуя (19) разностную схему для уравнения КдФ будем называть L2-консервативной, если для нее имеет место сеточный аналог второго интегрального закона сохранения, справедливого для дифференциальной задачи. 5.2. Явные разностные схемы (обзор). При построении разностных схем будем ориентироваться на простейшую разностную схему из работы (19) для линеаризованного уравнения КдФ, которое сохраняет свойства самого уравнения КдФ в смысле двух первых законов сохранения. Исследуем теперь схему (5.4) на свойства консервативности. Выполнение первого закона сохранения очевидно. Достаточно просто умножить это уравнение скалярно на 1. Тогда второе и третье слагаемые схемы (5.4) дадут 0, а от первого останется: Это сеточный аналог первого закона сохранения. Для вывода второго закона сохранения умножим скалярно уравнение (5.3) на 2τ у. Приходим к энергетическому тождеству Наличие отрицательного дисбаланса говорит не только о невыполнении соответствующего закона сохранения, но и ставит под сомнение вопрос вообще об устойчивости схемы в наиболее слабой норме L2( Другим примером явной двухслойной схемы является двух шаговая схема Лакса-Вендрофа (20). Это схема типа предиктор-корректор: В данный момент наиболее популярными схемами для уравнения КдФ считаются трехслойные схемы ввиду их простоты, точности и удобства реализации. Эту же схему можно представить в виде явной формулы Самой простой трехслойной схемой является следующая схема: Эта схема была использована при получении первых численных решений КдФ (8). Эта схема аппроксимирует дифференциальную задачу с порядком О (τ2 + h2). Согласно (21), схема является устойчивой при выполнении условия (при малых Ь): Приведем еще несколько схем. Трехслойная явная схема с порядком аппроксимации O(τ2 + h4)(20): Третья производная по пространству аппроксимируется на семиточечном шаблоне, а первая строится по пяти точкам. Согласно (21), эта схема устойчива при выполнении условия (при малых h): Легко видеть, что для этой схемы с более высоким порядком аппроксимации условие устойчивости является более жестким. В работе (19) предлагается следующая явная разностная схема с порядком аппроксимации О(τ2 + h2) : Так как разностное уравнение (5.8) можно записать в дивергентном виде то, скалярно умножив уравнение (5.9) на 1, получим следовательно, выполняется соотношение: которое можно считать сеточным аналогом первого закона сохранения. Таким образом, схема (5.8) является консервативной. В (19) доказано, что схема (5.8) является L2-консервативной и ее решение удовлетворяет сеточному аналогу интегрального закона сохранения 5.3. Неявные разностные схемы (обзор). В этом параграфе мы рассмотрим неявные разностные схемы для уравнения Кортевега-де Фриза. Вариант двухслойной схемы - неявная абсолютно устойчивая схема с порядком аппроксимации О (τ2, h4) (21): Решение разностной схемы (3.29) вычисляется с помощью семи диагональной циклической прогонки (22). Вопрос о консервативности этой схемы не исследовался. В работе (15) предлагается неявная трехслойная схема с весами: Разностная схемы (5.10) с периодическими по пространству решениями, консервативна, L2-консервативна при σ =1/2 и σ =1/4 для ее решения имеют место сеточные аналоги интегральных законов сохранения. 6. Численное решение Решалась начально-краевая задача на отрезке (0, 2π). В качестве начальных условий бралась функция u0(x)=sin (x). Явным образом было получено решение. Программа для расчетов была написана на языке Turbo Pascal 7.0. Текст основных частей программы прилагается. Расчеты велись на вычислительной машине с процессором AMD-K6-2 300 МГц с технологией 3DNOW!, размер оперативной памяти 32 Мб. 7. Заключение Настоящая работа посвящена исследованию уравнения Кортевега – де Фриза. Проведен обширный литературный обзор по теме исследования. Изучены различные разностные схемы для уравнения КдФ. Выполнен практический счет с использованием явной пяти точечной разносной схемы Как показал анализ литературных источников, явные схемы для решения уравнений типа КдФ наиболее применимы. В данной работе также решение было получено с использованием явной схемой. 8. Литература 1. Ландсберг Г.С. Элементарный учебник физики. М.: Наука, 1964. Т. 3. 2. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. М.: Мир, 1965. Вып.4. 3. Филиппов А. Г Многоликий солитон. М.: Наука, 1986. (Б-чка "Квант"; Вып. 48). 4. Рубанков В.Н. Солитоны, новое в жизни, науке, технике. М.: Знание, 1983. (Физика; Вып. 12). 5. Korteweg D.J., de Vries G. On the change form of long waves advancing in a rectangular channel and on new type of long stationary waves.//Phyl.May. 1895. e5. P. 422-443. 6. Сагдеев Р.З. Коллективные процессы и ударные волны в разреженной плазме.-В кн.: Вопросы теории плазмы, Вып.4. М.: Атомиз-дат, 1964, с.20-80. 7. Березин Ю.А., Карпман В.И. К теории нестационарных волн конечной амплитуды в разреженной плазме. // ЖЭТФ, 1964, т.46, вып.5, с. 1880-1890. 8. Zabusky N.J., Kruskal M.D. Interactions of "solitons"in a collisionless plasma and the reccurence of initial states // Phys.Rev.Lett. 1965. V.15. еб. Р.240-243. 9. Буллаф Р., Кодри Ф. Солитоны. М.: Мир; 1983 10. Sjoberg A. On the Korteweg-de Vries equation, existence and uniqueness, Uppsala University, Department of Computers, 1967 11. Temam R. Sur un probleme non lineare // J.Math.Pures Anal. 1969, V.48, 2, P. 159-172. 12. Лионе Ж.-Л. Некоторые методы решения нелинейных краевых задач. М.: Мир, 1972. 13. Кружков С.Н. Фаминский А.В. Обобщенные решения для уравнения Кортевега-де Фриза.// Матем. сборник, 1983, т. 120(162), еЗ, с.396-445 14.. Gardner C.S., Green J.M., Kruskal M.D., Miura R.M. Method for solving the Korteweg-de Vries equation // Phys.Rev.Lett. 1967. V. 19. P. 1095-1097. 15. Шабат А.Б. Об уравнении Кортевега-де Фриза // ДАН СССР, 1973, т.211, еб, с.1310-1313. 16. Фаминский А.В. Граничные задачи для уравнения Кортевега-де Фриза и его обобщений: Дисс.... докт. физ.-матем. наук,М:РУДН,2001 17. Miura R.M., Gardner C.S., Kruscal M.D. Korteweg-de Vries equation and generlization. II. Existence of conservation laws and constants of motion. // J.Math.Phys. 1968. V.9. P. 1204-1209. 18. Амосов А.А., Злотник А.А. Разностная схема для уравнений движений газа. 19. Самарский А.А., Мажукин В.И., Матус П.П., Михайлик И.А. Z/2-консервативные схемы для уравнения Кортевега-де Фриса.// ДАН, 1997, т.357, е4, с.458-461 20. Березин Ю.А. Моделирование нелинейных волновых процессов. Новосибирск: Наука. 1982. 21. Березин Ю.А., О численных решениях уравнения Кортевега-де Вриза.// Численные методы механики сплошной среды. Новосибирск, 1973, т.4, е2, с.20-31 22. Самарский А.А., Николаев Методы решения сеточных уравнений. М: Наука, 1978 23. Самарский А.А., Гулин А.В. Численные методы. М: Наука, 1989 24. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М: Наука, 1987 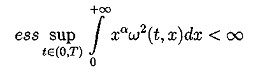 (4.1)
(4.1)![]() , вводится класс корректности задачи (3.2),(1.4) и устанавливаются теоремы единственности и непрерывной зависимости решений этой задачи от начальных данных. Также исследуются вопросы регулярности обобщенных решений. Одним из основных результатов является достаточное условие существования непрерывной по Гельдеру при t > 0 производной
, вводится класс корректности задачи (3.2),(1.4) и устанавливаются теоремы единственности и непрерывной зависимости решений этой задачи от начальных данных. Также исследуются вопросы регулярности обобщенных решений. Одним из основных результатов является достаточное условие существования непрерывной по Гельдеру при t > 0 производной ![]() в терминах существования моментов для начальной функции, для любых k и l.
в терминах существования моментов для начальной функции, для любых k и l.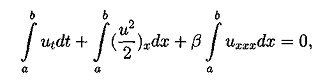
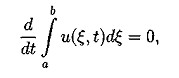
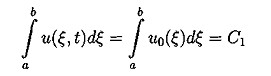 (4.2)
(4.2)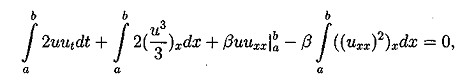
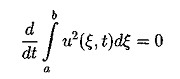
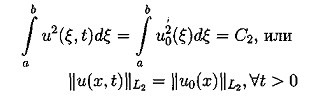 (4.3)
(4.3)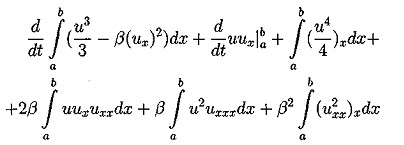
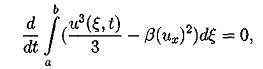
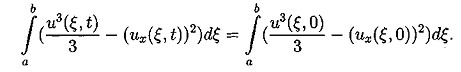 (4.4)
(4.4)![]() ={(x,t):0≤x≤l,0≤t≤T} обычным образом введем равномерные сетки, где
={(x,t):0≤x≤l,0≤t≤T} обычным образом введем равномерные сетки, где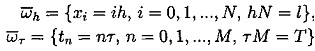
![]() со значениями в узлах сетки yi=yh(xi). Предполагается, что выполнены условия периодичности y0=yN. Кроме того, формально полагаем yi+N=yi для i ≥ 1.
со значениями в узлах сетки yi=yh(xi). Предполагается, что выполнены условия периодичности y0=yN. Кроме того, формально полагаем yi+N=yi для i ≥ 1.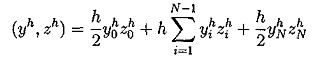
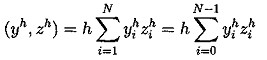 (5.1)
(5.1)![]()
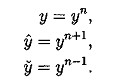
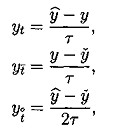
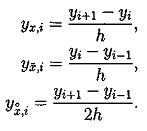
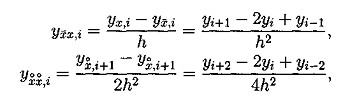
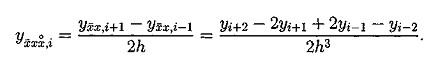
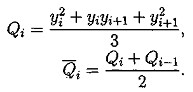 (5.2)
(5.2)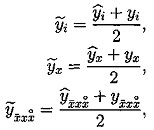
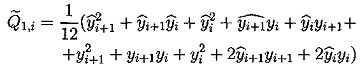
![]() 1 выполняется равенство:
1 выполняется равенство: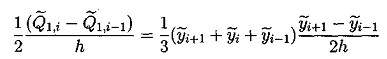
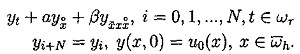 (5.3)
(5.3)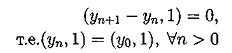 (5.4)
(5.4)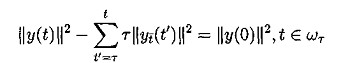 (5.5)
(5.5)![]() ).)- В работе (15) показано, что схемы семейства (3.18) являются абсолютно неустойчивыми в норме L2(
).)- В работе (15) показано, что схемы семейства (3.18) являются абсолютно неустойчивыми в норме L2(![]() ).
).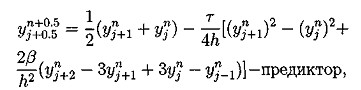
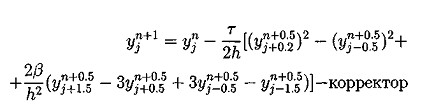
![]() (5.6)
(5.6)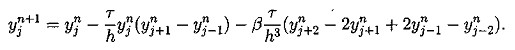 (5.7)
(5.7)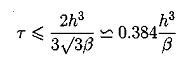
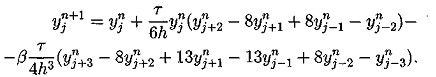
![]()
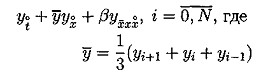 (5.8)
(5.8)![]() (5.9)
(5.9)![]()
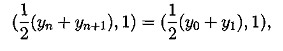
![]()
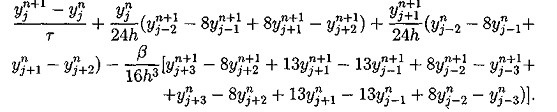
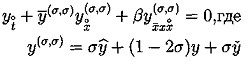 (5.10)
(5.10)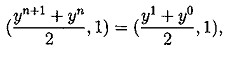
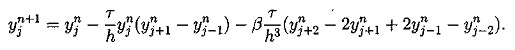 (5.7)
(5.7)