Сжатие речевого сигнала на основе линейного предсказания

Введение

Одной из задач такого обширного раздела как «Цифровая обработка речевых сигналов», входящего в состав науки, занимающейся цифровой обработкой сигналов или просто обработкой сигналов является сжатие или кодирование речевого сигнала (РС). Сжатие РС может быть как без потерь (архивация), так и с потерями. Причем в последнем случае это кодирование можно подразделить на три вида:

кодирование непосредственно реализации РС (Wave Form Codec);
измерение, кодирование и передача на приемную сторону параметров РС, по которым уже на приемной стороне производится синтез этого (искусственного) РС. Такие системы называют вокодерными (Source Codec);
гибридные способы кодирования, т.е. сочетание первого и второго способов кодирования. В задачу данной работы входит рассмотрение первого способа кодирования.

Под кодированием подразумевается преобразование РС в некоторый «другой» сигнал, который можно представить с меньшим числом разрядов, что в итоге повысит скорость передачи данных. Одним из видов такого кодирования является дифференциальная импульсно-кодовая модуляция (ДИКМ), о которой и пойдет речь в дальнейшем.

Дифференциальная импульсно-кодовая модуляция

В обычной импульсно-кодовой модуляции каждый отсчет кодируется независимо от других. Однако у многих источников сигнала при стробировании с частотой Найквиста или быстрее проявляется значительная корреляция между последовательными отсчетами (1) (в частности, источник РС является квазистационарным источником и может относиться к рассматриваемым видам источников). Другими словами, изменение амплитуды между последовательными отсчетами в среднем относительно малы. Следовательно, схема кодирования, которая учитывает избыточность отсчетов, будет требовать более низкой битовой скорости.

Суть ДИКМ заключается в следующем. Предсказывается текущее значение отсчета на основе предыдущих M отсчетов. Для конкретности предположим, что означает текущий отсчет источника, и пусть обозначает предсказанное значение (оценку) для , определяемое как

Таким образом, является взвешенной линейной комбинацией M отсчетов, а являются коэффициентами предсказания. Величины выбираются так, чтобы минимизировать некоторую функцию ошибки между и . Проиллюстрируем вышесказанное на отрезке РС:

Прежде чем идти дальше, рассмотрим виды предсказания. «Линейное» предсказание означает, что является линейной функцией предыдущих отсчетов; при «нелинейном» предсказании – это нелинейная функция. Порядок предсказания определяется количеством используемых предыдущих отсчетов. То есть, предсказание нулевого и первого порядка является линейным, а второго и более высокого порядка - нелинейным. При линейном предсказании восстановить сигнал значительно проще, чем при нелинейном предсказании. Будем рассматривать только линейное предсказание.

Виды линейных предсказаний

Предсказание нулевого порядка.

В этом случае для предсказания текущего отсчета используется только предыдущий отсчет РС, т.е.

Предсказание первого порядка (линейная экстраполяция).

В этом случае для предсказания текущего отсчета используется не только предыдущий отсчет, но и разница между предпоследним и последним отсчетами, которая суммируется к общему результату:

Коэффициенты линейного предсказания (получение и расчет)

Формирование сигнала ошибки при использовании линейного предсказания эквивалентно прохождению исходного сигнала через линейный цифровой фильтр. Этот фильтр называется фильтром сигнала ошибки (ФСО) или обратным фильтром.

Обозначим передаточную функцию такого фильтра как А(z):

где E(z) и X(z) – прямое z - преобразование от сигнала ошибки и входного сигнала соответственно.

На приемной стороне при прохождении сигнала ошибки через формирующий фильтр (ФФ) мы в идеале получим исходный сигнал. Обозначим передаточную функцию формирующего фильтра как K(z).

Т.е. передаточная функция K(z) связана с A(z) следующим соотношением:

Рассмотрим последовательно соединенные кодер и декодер:

При условии, что A(z)K(z) = 1, будет обеспечено абсолютно точное восстановление сигнала, т.е. . Но это в идеале, на самом деле такого быть не может по причинам, о которых скажем ниже.

Для примера, найдем передаточные функции ФСО и ФФ для разных типов линейного предсказания.

а) предсказание нулевого порядка;

; ;

Получили, что такой фильтр неустойчив (граница устойчивости), так как полюс находится на единичной окружности.

б) предсказание первого порядка;

;;

Получили, что и такой фильтр тоже неустойчив (граница устойчивости).

в) общая форма предсказания;

Было получено, что => .

; ;

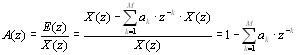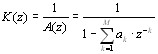На основании рассмотренных примеров можно сделать следующие выводы.

Фильтр сигнала ошибки всегда является КИХ фильтром, а формирующий фильтр – БИХ фильтром. Коэффициенты передаточной функции ФФ, которые, как уже было сказано выше, являются коэффициентами линейного предсказания (LPC: Linear Prediction Coefficients), должны быть такими, чтобы:

формирующий фильтр был устойчивым;
ошибка 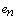была минимальна.

Для получения передаточной функции ФФ, наиболее точно воспроизводящего частотную характеристику голосового тракта для данного звука, следует определять коэффициенты передаточной функции исходя из условия наименьшей ошибки линейного предсказания речевого сигнала (по условию минимума среднего квадрата ошибки).

Запишем выражение для оценки дисперсии сигнала ошибки, которую надо свести к минимуму:

; ;

Получили, что - функция нескольких переменных. Продифференцируем ее и приравняем частные производные для нахождения экстремума:

; ,

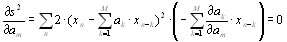где - символ Кронекера. Следовательно: ;

; => ;

Получили нормальные уравнения или уравнения Юла-Волкера. Введем обозначение: , где - есть ни что иное, как корреляционная функция. Перепишем полученное выражение с учетом принятого обозначения:

(*)

Для вычисления функции необходимо определить пределы суммирования по n: , где N – количество отсчетов в сегменте РС, а M - количество отсчетов, необходимых для расчета коэффициентов предсказания (M + 1)-го отсчета. Значит, первое предсказанное значение запишется так: , где n = M + 1.

Получили:

;

Обозначим n – k = j => n = k + j, n – m = k + j – m <=> n – m = i + j, где i = k – m. Следовательно:

Таким образом, получается выражение, имеющее структуру кратковременной ненормированной АКФ, но зависящей не только от относительного сдвига последовательности i, но и от положения этих последовательностей внутри сегмента РС, которые определяются индексом k, входящим в пределы суммирования. Такой метод определения функции называется ковариационным.

Выражение (*) представляет собой систему линейных алгебраических уравнений (СЛАУ) относительно , у которых все коэффициенты различны.

При использовании ковариационного метода получаются несмещенные оценки коэффициентов линейного предсказания, то есть E{ak}= ak.ист, где ak.ист – истинные значения коэффициентов линейного предсказания.

Другой способ определения коэффициентов системы (*) состоит в том, что вместо функции используется некоторая другая функция , которая определяется как

где - ненормированная кратковременная АКФ. Поскольку определение функции сводится к расчету АКФ, то такой метод называется автокорреляционным. При использовании этого метода мы получаем смещенные оценки коэффициентов линейного предсказания (однако, при M << N смещение пренебрежимо мало).

Перепишем СЛАУ (*) с учетом введенной функции :

При использовании автокорреляционного метода вся информация о сигнале, необходимая для определения коэффициентов линейного предсказания, содержится в кратковременной ненормированной АКФ B(i).

Распишем полученную систему линейных алгебраических уравнений (СЛАУ) в явном виде:

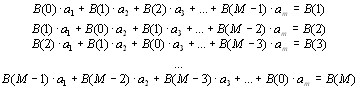
Перепишем ее в матричной форме:

;

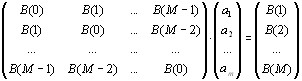Свойства матрицы коэффициентов системы:

матрица симметрична;
матрица Теплица (матрица, в пределах каждой диагонали которой все элементы равны);

Для решения СЛАУ с такой матрицей используется алгоритм Левинсона – Дурбина, который требует меньших вычислительных затрат, чем стандартные алгоритмы. Он выглядит следующим образом.

Начальные значения для алгоритма:

Алгоритм:

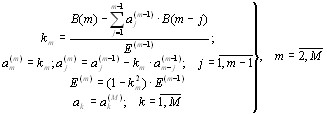
Решетчатый фильтр сигнала ошибки предсказания

В предыдущем разделе приводилась процедура вычисления коэффициентов предсказания Левинсона-Дурбина. В этой процедуре, как промежуточные величины, используются некоторые коэффициенты km, которые называются коэффициентами отражения. Их физический смысл заключается в следующем. Голосовой тракт человека представляет собой трубу, состоящую из секций, соединенных последовательно, но имеющих разный диаметр. При прохождении звуковой волны через такую систему, возникают отражения на стыках секций, т.к. каждый стык является неоднородностью. Коэффициент отражения характеризует величину проходимости стыка двух секций (сред). Коэффициент отражения равен:

Поясним его смысл на следующем рисунке («жирным» показана m – секция голосового тракта):

Если rm = -1, то произойдет обрыв в цепи передачи сигнала (обрыв прямой ветви). Такого быть не должно, поэтому необходимо следить за этим.

Модель акустических труб может быть представлена в виде фильтра, имеющего решетчатую (или лестничную) структуру. Основными параметрами такого фильтра являются коэффициенты отражения.

Система акустических труб – резонансная система, поэтому если фильтр без потерь, то на его АЧХ будут наблюдаться разрывы (всплески в бесконечность). Реально на месте этих всплесков будут резонансные пики, и резонансные частоты таких пиков называются формантными. Обычно в реальных голосовых трактах человека формантных частот (или формант) не более трех. Более подробно о коэффициентах отражения и решетчатых фильтрах можно прочитать в (2, глава 3).

Так как коэффициенты отражения и коэффициенты предсказания вычисляются в рамках одной и той же процедуры алгоритма Левинсона-Дурбина, то они могут быть выражены друг через друга. Приведем здесь эти алгритмы.

Прямая рекурсия (коэффициенты отражения а коэффициенты предсказания):

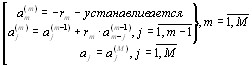
Обратная рекурсия (коэффициенты предсказания а коэффициенты отражения):

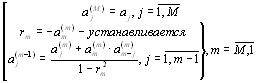
Как уже было сказано, фильтры сигнала ошибки представляют собой КИХ фильтры или нерекурсивные фильтры, что означает отсутствие ветвей обратной связи. Системы с КИХ также могут обладать строго линейной ФЧХ. Линейность ФЧХ является очень важным обстоятельством применительно к РС в тех случаях, когда требуется сохранить взаимное расположение элементов сигнала. Это существенно облегчает задачу их проектирования и позволяет уделять лишь внимание аппроксимации их АЧХ. За это достоинство приходится расплачиваться необходимостью аппроксимации протяженной импульсной реакции в случае фильтров с крутыми АЧХ (2).

Изобразим граф фильтра, имеющего решетчатую структуру, на примере фильтра 3–го порядка:

В отличие от формирующего фильтра этот фильтр имеет один вход и два выхода:

1) ei – последовательность отсчетов сигнала ошибки прямого линейного предсказания;

2) bi – последовательность отсчетов сигнала ошибки обратного линейного предсказания.

Важность bi определяется тем, что по нему совместно с сигналом ошибки ei могут быть оценены коэффициенты отражения.

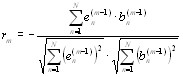где N – количество отсчетов в сегменте.

Полученная формула для расчета коэффициентов отражения имеет также другой физический смысл. Это не что иное, как коэффициент корреляции между последовательностью отсчетов сигнала ошибки прямого и обратного линейных предсказаний.

Приведем также рекуррентные разностные уравнения решетчатого фильтра сигнала ошибки:

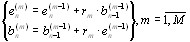
выход фильтра;

Начальные условия для этой рекуррентной процедуры:

Реализация ДИКМ

Имея метод определения коэффициентов предсказания, рассмотрим блок-схему практической системы ДИКМ, показанную ниже.

В этой схеме предсказатель стоит в цепи обратной связи, охватывающей квантователь. Вход предсказателя обозначен . Он представляет собой сигнальный отсчет , искаженный в результате квантования сигнала ошибки. Выход предсказателя равен:

; (**)

Разность является входом квантователя, а обозначает его выход. Величина квантованной ошибки предсказания кодируется последовательностью двоичных символов и передается через канал в пункт приема. Квантованная ошибка также суммируется с предсказанной величиной , чтобы получить .

В месте приема используется такой же предсказатель, как на передаче, а его выход суммируется с , чтобы получить (см. рис. ниже).

Сигнал является входным воздействием для предсказателя и в то же время образует входную последовательность, по которой с помощь ЦАП восстанавливается сигнал x(t). Использование обратной связи вокруг квантователя обеспечивает то, что ошибка в - просто ошибка квантования и что здесь нет накопления предыдущих ошибок квантования при декодировании. Имеем

Следовательно, . Это означает, что квантованный отсчет отличается от входа ошибкой квантования независимо от использования предсказателя. Значит, ошибки квантования не накапливаются.

В рассмотренной выше системе ДИКМ оценка или предсказанная величина отсчета сигнала получается посредством линейной комбинации предыдущих значений , k = 1, 2, …, M, как показано в формуле (**). Улучшение качества оценки можно получить включением в оценку линейно отфильтрованных последних значений квантованной ошибки.

Конкретно, оценку можно выразить так:

где {} – коэффициенты фильтра для квантованной последовательности ошибок . Блок-схемы кодера на передаче и декодера на приеме приведены ниже.

Здесь два ряда коэффициентов {} и {} выбираются так, чтобы минимизировать некоторую функцию ошибки , например среднеквадратическую ошибку.

Адаптивная дифференциальная импульсно-кодовая модуляция

Многие реальные источники (например, источники РС), как уже было сказано выше, являются квазистационарными по своей природе. Одно из свойств квазистационарности характеристик случайного выхода источника заключается в том, что его дисперсия и автокорреляционная функция медленно меняются со временем. Кодеры ИКМ и ДИКМ, однако, проектируются в предположении, что выход источника стационарен. Эффективность и рабочие характеристики таких кодеров могут быть улучшены, если они будут адаптироваться к медленно меняющейся во времени статистике источника. Как в ИКМ, так и в ДИКМ ошибка квантования , возникающая в равномерном квантователе, работающем с квазистационарным входным сигналом, будет иметь меняющуюся во времени дисперсию (мощность шума квантования).

Одно улучшение, которое уменьшает динамический диапазон шума квантования, - это использование адаптивного квантователя. Другое – сделать адаптивным предсказатель в ДИКМ. При этом коэффициенты предсказателя могут время от времени меняться, чтобы отразить меняющуюся статистику источника сигнала. И полученная СЛАУ, для решения которой используется алгоритм Левинсона – Дурбина, остается справедливой и с краткосрочной оценкой автокорреляционной функции B(i) (при принятых обозначениях B(i) – уже кратковременная АКФ), поставленной вместо оценки функции корреляции по ансамблю. Определенные таким образом коэффициенты предсказателя могут быть вместе с ошибкой квантования переданы приемнику, который использует такой же предсказатель. К сожалению, передача коэффициентов предсказателя приводит к увеличению необходимой битовой скорости, частично компенсируя снижение скорости, достигнутое посредством квантователя с немногими битами (немногими уровнями квантования) для уменьшения динамического диапазона ошибки , получаемой при адаптивном предсказании.

В качестве альтернативы предсказатель приемника может вычислить свои собственные коэффициенты предсказания через и , где

;

Если пренебречь шумом квантования, эквивалентно . Следовательно, можно использовать для оценки АКФ B(i) в приемнике, и результирующие оценки могут быть использованы в СЛАУ вместо B(i) при нахождении коэффициентов предсказателя. При достаточно большом числе уровней квантования разность между и очень мала. Следовательно, оценка B(i), полученная через , может быть использована для определения коэффициентов предсказателя. Выполненный таким образом адаптивный предсказатель приводит к низкой скорости кодирования данных источника.

Вместо использования блоковой обработки для нахождения коэффициентов предсказателя {}, как описано выше, мы можем адаптировать коэффициенты предсказателя поотсчетно, используя алгоритм градиентного типа, который мы и рассмотрим.

Основное преимущество такого метода адаптации – это отказ от решения СЛАУ, что значительно уменьшает вычислительные затраты.

Запишем оценку среднего квадрата ошибки предсказания:

Изобразим два графика, объясняющих функциональную зависимость в одномерном случае () и в двумерном случае ():

Очевидно, что в общем случае, т.е. при фигура, полученная при двух коэффициентах предсказания, превратится в многомерный параболоид. Цель градиентного метода состоит в том, чтобы найти такой вектор аорt, при котором функция s2 будет иметь наименьшее значение, т.е. после определенных итераций необходимо достичь вершины этого параболоида. Алгоритм такого градиентного метода выглядит так:

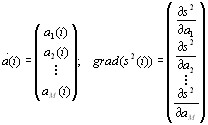
где i – номер шага, μ – шаг алгоритма.

При малом шаге алгоритма мы практически полностью устраняем возможность расхождения алгоритма, но при этом проигрываем в скорости сходимости или в скорости нахождения коэффициентов предсказателя. И наоборот.

Следует сказать, что такой алгоритм сходится при очень большом количестве итераций, в общем случае, при количестве итераций стремящемся к бесконечности. Поэтому необходимо также перед началом вычислений задаться допустимой погрешностью, которая нас может устроить.

Найдем частную производную:

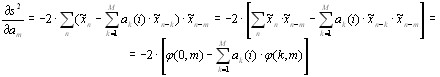
Тогда алгоритм адаптации коэффициентов линейного предсказания примет следующий вид:

Иллюстрации

Ниже приводятся иллюстрации одного из опытов, проделанного в лабораторной работе.

Обрабатываемый сегмент речевого сигнала:

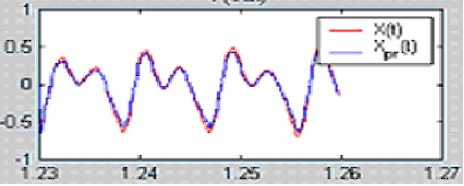
Ошибка предсказания:

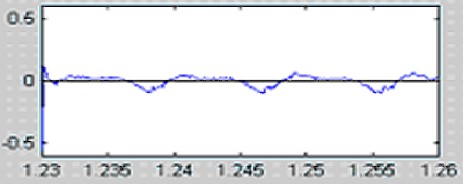
Коэффициенты отражения и Импульсная характеристика формирующего фильтра:

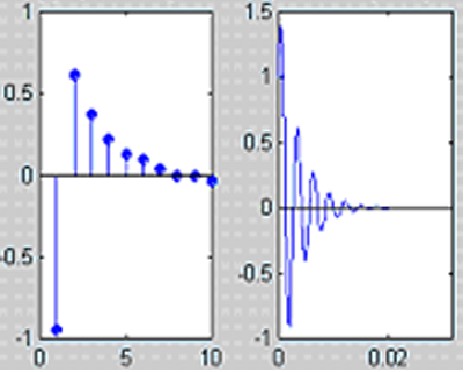
Передаточные функции ФФ и ФСО и Диаграмма полюсов:

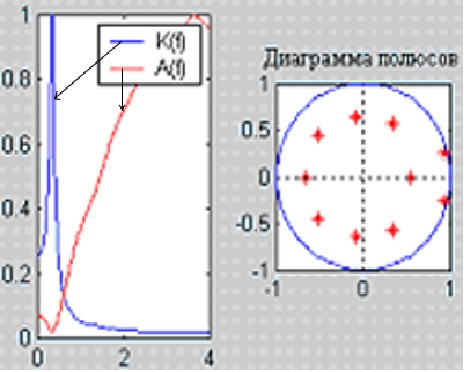
Полученный (синтезированный) сегмент РС:

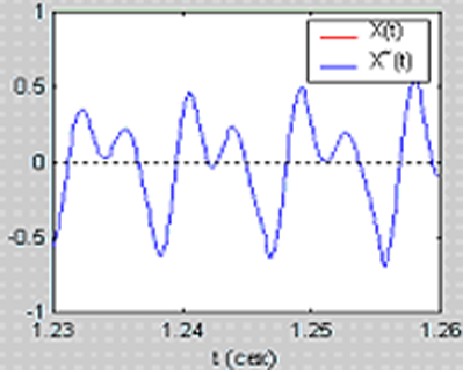
Ошибка предсказания:

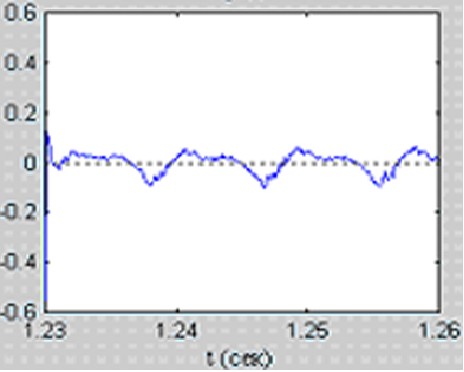
В проделанной работе проводились исследования влияния разрядности коэффициентов предсказания / отражения и сигнала ошибки на синтезированный сигнал в системе с АДИКМ, полученный по этим величинам на приемной стороне декодером. Как уже ясно из названия коэффициентов, исследовались и сравнивались два типа фильтров: стандартный и решетчатый.

В результате можно сделать следующие выводы.

Решетчатый фильтр всегда устойчив и коэффициенты отражения всегда меньше 1, потому что коэффициенты отражения являются также и коэффициентами корреляции. Устойчивость решетчатого фильтра инвариантна к разрядности коэффициентов отражения. Разрядность коэффициентов отражения сказывается лишь на форме передаточной функции и, как следствие, на диаграмме полюсов и импульсной характеристике, а на форму синтезированного РС влияет очень незначительно, при условии постоянной, довольно высокой (12) разрядности сигнала ошибки.

В случае фиксированной, довольно низкой, разрядности коэффициентов отражения (4) и уменьшающейся разрядности сигнала ошибки до значения (6), ухудшение синтезированного РС незначительно. При числе разрядов меньше (6) уже начинают наблюдаться значительные искажения. Если сравнить эти опыты с опытами, проделанными над стандартным фильтром, то для того же сегмента и при значении разрядности (8), наблюдалась неустойчивость синтезированного фильтра и, как следствие, полное искажение РС.

В случае, если два фильтра были устойчивы и разрядность их коэффициентов, а также разрядность сигнала ошибки была одинаковой, то синтезированный сигнал оказывался идентичным.

Следует также отметить не только влияние разрядности коэффициентов предсказания / отражения на синтезированный сигнал, но и, прежде всего, саму реализацию исходного аналогового РС, как основы, по которой рассчитываются сами коэффициенты. Поэтому необходимо иметь запас по разрядности коэффициентов предсказания, чтобы стандартный фильтр для некоторых реализаций не оказался неустойчив (решетчатый фильтр устойчив в любом случае). Экспериментально был подобран вариант выбора разрядности коэффициентов предсказания (12), а сигнала ошибки (8) (разрядность коэффициентов отражения не играет почти никакой роли). Это достаточно хорошо различимая речь.

Заключение

В данной работе достаточно подробно изложен метод цифрового сжатия речевого сигнала на основе линейного предсказания. Показано, что существуют несколько подходов к решению этой задачи. Приведены иллюстрации из проделанной лабораторной работы со всеми необходимыми комментариями и выводами.

Список литературы

Прокис Дж., «Цифровая связь», - М: Радио и связь, 2000.
Рабинер Л.Р., Шафер Р.В., «Цифровая обработка РС», - М: Радио и связь, 1981.
Конспект лекций по курсу «Цифровая обработка РС», 2004.