Основные представления о внутреннем строении вещества

Основные представления о внутреннем строении вещества

Реальность атомов и молекул.

Согласно кинетической теории газов лишь очень небольшая (при обычных условиях примерно одна десятитысячная) доля всего объёма газа занята самими молекулами, которые находятся в состоянии непрерывного беспорядочного движения. Каждая молекула ежесекундно несколько миллиардов раз сталкивается с другими, поэтому средняя длина её свободного пробега измеряется лишь десятками миллиметров.

Кинетические представления М.В. Ломоносова наиболее полно развиты в его работе “Опыт теории упругости воздуха” (1748 г.). “Атомы воздуха,— писал Ломоносов, — в нечувствительные промежутки времени сталкиваются с другими, сходными, в беспорядочной взаимности, и когда одни находятся в соприкосновении, другие отрываются друг от друга и снова сталкиваются с другими, более близкими, снова отскакивают, так что стремятся рассеяться во все стороны, постепенно отталкиваемые друг от друга такими очень частыми взаимными ударами”

Средняя скорость молекул основных газов воздуха — азота и кислорода — составляет при обычных условиях около 460 м/с, среднее число столкновений каждой молекулы за секунду — около 7 миллиардов, а средняя длина свободного пробега — около 70 нм. Так как средняя длина свободного пробега обратно пропорциональна давлению газа, под вакуумом, например, в миллионную долю миллиметра ртутного столба она составляет уже около 50 м. Практически это означает, что молекулы при таком вакууме несравненно чаще будут сталкиваться со стенками заключающего газ сосуда, чем друг с другом.

Ударяясь о ту или иную преграду, молекулы производят на неё давление, которое является суммарным результатом толчков молекул. Оказываемое давление будет тем значительнее, чем больше толчков за единицу времени и чем сильнее каждый из них. Одним из важнейших выводов кинетической теории было то, что при данной температуре средняя кинетическая энергия поступательного движения молекул не зависит от их природы; иначе говоря, с извинением массы молекул скорости их изменяются так, что средняя кинетическая энергия остаётся постоянной. Поэтому давление должно зависеть только от числа молекул (в единице объёма).

В воздухе у земной поверхности площадь размером в 1 см3 испытывает 1023 ударов молекул за секунду. Но по мере удаления от земной поверхности давление воздуха уменьшается. Поэтому чем выше находится слой газа, тем меньше в нём концентрация молекул. Кинетическая теория даёт возможность рассчитывать изменение концентрации с высотой для частиц любой массы.

Очевидно, что если бы удалось доказать правильность расчётов кинетической теории при опытах с учётом поведения каждой отдельной частицы, то тем самым были бы подтверждены молекулярно-атомистические представления. Но главная сложность связана с ничтожными размерами молекул.

Перрен устранил это затруднение, воспользовавшись более крупными частицами. В результате долгой кропотливой работы ему удалось наделать из некоторых смолистых веществ шариков приблизительно одинакового радиуса — порядка десятых долей микрона. Такие частицы хорошо видны под микроскопом. Зная их радиус и плотность применённого для изготовления вещества, легко вычислить массу каждого шарика. Будучи разболтаны с водой (или другой жидкостью) в маленькой стеклянной камере, они первоначально занимают весь объём равномерно, но затем, после отстаивания, устанавливается определённое распределение частиц по высоте. Производя при помощи микроскопа подсчёт числа частиц в единице объёма на разных высотах можно проверить совпадают ли результаты с требованием кинетической теории.

Наиболее трудной частью исследования Перрена было приготовление шариков определённых размеров. “Мне пришлось,— пишет он,— обработать 1 кг гуммигута, чтобы получить через несколько месяцев фракцию, содержащую несколько дециграммов зёрен, диаметр которых был весьма близок к той величине, какую хотелось получить”. Сами опыты проводились при очень различных условиях: температура изменялась от –9 до +58 °С, вязкость среды — в отношении 1:330, масса шариков — в отношении 1:70 000 и т.д.

Подсчёт частиц на различных высотах производился в очень узком поле зрения, причём выводилось среднее из многих отдельных отсчётов. Например, при одном из опытов с гуммигутовыми шариками радиусом 0,21 мк отсчёты производились на высоте 5, 35, 65 и 95 мк от дна камеры. По теории, отношение числа частиц на этих высотах ожидалось в данном случае равным 100:48:23:11. При проведении опытов было пересчитано 13 000 шариков, причём результаты относительного распределения по высотам выразились цифрами 100:47:23:12.

Совпадение результатов Перрена с требованиями кинетической теории как при распределении частиц по высоте, так и при проверке других вытекающих из этой теории следствий получилось блестяще. После этого стало уже невозможно возражать против реальности молекул, и приблизительно к 1910 г. молекулярно-атомистические представления вновь стали общепринятыми.

Еще значительно раньше, во второй половине ХIХ века, были сделаны попытки подойти к вопросу об абсолютной массе и размерах атомов и молекул. Взвесить отдельную молекулу явно невозможно, однако теория открыла другой путь: надо было как-то определить число молекул в моле — так называемое число Авогадро (N). Непосредственно сосчитать молекулы так же невозможно, как и взвесить их, но число Авогадро входит во многие уравнения различных отделов физики, и его можно, исходя из этих уравнений, вычислить. Очевидно, что если результаты таких вычислений, произведённых несколькими независимыми путями, совпадут, то это может послужить доказательством правильности найденной величины.

Результаты первых определений числа Авогадро

Метод N.1023 Метод N.1023

Голубой цвет неба 6,04 Радиоактивные явления 6,04

Теория излучения 6,05 Структура спектральных линий 6,08

Распределение частиц по высоте 6,05 Строение кристаллов 6,04

Электрические заряды частиц 6,02 Поверхностное натяжение растворов 6,00

Результаты первых определений числа Авогадро сопоставлены выше. Все они, несмотря на различие использованных методов, очень близки друг к другу. В настоящее время значение числа Авогадро принимается равным 6,02.1023. Некоторое представление о громадности этой величины можно получить, исходя из следующих данных: если бы всё население Земли (около 4 миллиардов человек) стало бы считать молекулы, содержащиеся в одном моле, то при непрерывном отсчёте каждым человеком по одной молекуле в секунду для выполнения работы потребовалось бы около 5 миллионов лет.

Уточнённое значение числа Авогадро равно (6,0225±0,0003).1023. На его основе формулируется расширенное понятие моль; как число единиц любого вида (молекул, атомов, электронов и др.), равное числу Авогадро.

Зная число Авогадро, легко найти абсолютную массу частицы любого вещества. Действительно, абсолютная масса (в граммах) единицы атомных и молекулярных весов равна 1/N, т. е. 1,66.10–24 г. Масса эта во столько же раз меньше массы маленькой дробинки, во сколько раз масса человека меньше массы всего земного шара.

Пользуясь числом Авогадро, можно оценить также размеры атомов. Например, атомный вес натрия равен 23,0 и плотность его — 0,97 г/см3. Объём, занимаемый молем натрия (т. н. атомный объём), равен, следовательно, 23: 0,97 = = 23,7 см3. Так как моль содержит 6,02.1023 атомов, на долю каждого приходится 23,7/6,02.1023 = 3,9.10–23 см3, что соответствует кубику с длиной ребра 340 пм.

В действительности правильнее рассматривать атомы не как кубики, а как шары, причём определение радиуса атома Na более точными методами даёт 186 пм. Радиусы других атомов также выражаются величинами порядка сотен пикометров.

До конца прошлого столетия физика и химия имели мало точек соприкосновения. Лишь в ХХ веке была стёрта резкая граница между обеими науками. Пограничные области назывались физической химией и химической физикой.

Хотя начало первой из них было положено ещё М.В. Ломоносовым (1752 г.), широко развилась она лишь в конце ХIX века и имела своим содержанием применение к обычным химическим проблемам теоретических и экспериментальных методов физики. Областью второй, целиком развившейся в ХХ веке, являлось изучение внутреннего строения атомов и молекул и изменений их в процессе химических реакций.

“Физическая химия — наука, которая должна на основании положений и опытов физических объяснить причину того, что происходит через химические операции в сложных телах”. Такое определение даёт М. В. Ломоносов в своём “Курсе истинной физической химии” (1752 г.). Как и во многих других случаях, он опередил современную ему науку более чем на столетие. Следующий по времени курс физической химии читался Н. Н. Бекетовым (1865 г.). Важность данной дисциплины была широко осознана лишь к концу XIХ в.

Вопрос о внутреннем строении атомов и молекул интересовал уже М. В. Ломоносова. “Bо тьме должны обращаться физики, а особливо химики, не зная внутреннего нечувствительных частиц строения”, — писал он, ставя перед наукой будущего те задачи, которые разрешаются в настоящее время химической физикой.

Различие между физической химией и химической физикой до известной степени условно (и вторую часто включают в первую). Вместе с тем, каждая из них может быть довольно чётко отграничена от другой: предметом физической химии (классической) является суммарное рассмотрение химических процессов, протекающих с одновременным участием множества частиц, тогда как предметом химической физики — рассмотрение отдельных частиц и взаимодействий между ними, т. е. элементарных процессов.

Атомы “не неделимы по своей природе, а неделимы только доступными нам средствами и сохраняются лишь в тех химических процессах, которые известны теперь, но могут быть разделены в новых процессах, которые будут открыты впоследствии”. Это гениальное предвидение А. М. Бутлерова (1886 г.) не было понято и принято его современниками. В сознании учёных, твёрдо стоявших на точке зрения атомистической теории, укрепилось представление об атомах, как о последних, ни при каких условиях неделимых частицах вещества. Из-за этого на несколько лет задержалось правильное истолкование важного открытия, сделанного Беккерелем в 1896 г.

Известно было, что существуют вещества, которые после предварительного освещения светятся затем некоторое время сами. Явление это называется фосфоресценцией. Изучать его можно, в частности, по действию испытуемых материалов на фотографическую пластинку. Исследуя таким образом различные вещества, Беккерель заметил, что образцы, содержащие в своём составе уран, действуют на фотографическую пластинку и без предварительного освещения.

Заинтересовавшись этими опытами и продолжая их, М. Сколдовская-Кюри обратила внимание на то, что действие на фотографическую пластинку природных руд урана сильнее, чем чистой его окиси, несмотря на большее процентное содержание урана в последней. Это навело её на мысль, что урановые минералы содержат в своём составе какой-то неизвестный элемент, более активный, чем сам уран. В результате тщательной и кропотливой работы Кюри в 1898 г. удалось выделить из урановой руды два новых элемента — полоний и радий. Оказалось, что оба они действуют на фотографическую пластинку несравненно сильнее урана.

Само явление, изучавшееся в дальнейшем преимущественно на соединениях радия, было названо радиоактивностью. Опыт показывал, что активность препарата определяется исключительно содержанием в нём радия и совершенно не зависит от того, в виде какого соединения он находится. Активность препарата практически не зависит также и от внешних условий: нагревание или охлаждение, действие света, электричества и т. д. не оказывают на неё сколь-нибудь заметного влияния. Все эти факторы заставляли сделать предположение, в корне противоречащее установившимся взглядам, — предположение, что радиоактивные явления обязаны своим происхождением самопроизвольному распаду атомов радия и других радиоактивных элементов. Тем самым был поставлен вопрос о внутреннем строении атома.

Исследование радиоактивного излучения показало, что оно является сложным. Если радиоактивный препарат, заключённый в непроницаемую для его лучей свинцовую капсулу с отверстием наверху, поместить в электрическое поле, то излучение распадается на три составные части, так называемые α, β и γ–лучи. Первые отклоняются к отрицательному полюсу; они представляют собой поток частиц сравнительно большой массы, заряженных положительно. Вторые сильнее отклоняются к положительному полюсу; они слагаются из частиц очень малой массы, заряженных отрицательно. Наконец, γ-лучи представляют собой волны, подобные световым лучам, но более короткие. Аналогичное расщепляющее действие на радиоактивное излучение оказывает магнитное поле. Все три вида лучей действуют на фотографическую пластинку, вызывают свечение некоторых веществ и т.д.

Ещё до открытия радиоактивности было известно, что при прокаливании металлов, а также при освещении их ультрафиолетовыми лучами поверхность металла испускает отрицательное электричество. Вопрос о природе этого электричества был выяснен опытами с катодными лучами, которые получаются при электрическом разряде в разряжённом пространстве. Для их изучения использовалась установка: стеклянный сосуд, из которого выкачан воздух, впаяны анод и катод. При разрядке между ними от катода распространяются катодные лучи, которые частично проходят сквозь узкое отверстие в аноде, затем между двумя металлическими пластинками и наконец попадают в пространство, где могут быть обнаружена при помощи фотографирования или иными путями. Если между пластинками создать электрическое поле, то лучи отклоняются в сторону пластинки, заряженной положительно,— это показывает, что сами лучи заряжены отрицательно. Изменяя условия опыта (силу поля и др.), можно изучить различие между этими лучами.

В результате подобных опытов выяснилось, что катодные лучи являются потоком отрицательно заряженных частиц с очень малой массой. Этот вывод был подтверждён дальнейшими исследованиями, причём оказалось, что частички, испускаемые металлами при их нагревании или освещении, равно как частички катодных лучей и β-лучи, представляют собой одно и то же. Частички эти были названы электронами.

До работ с катодными лучами считалось, что количество электричества может изменяться непрерывно. После этих работ стали склоняться к противоположному мнению. Уже в конце ХIХ века удалось получить приблизительно правильную оценку величины наименьшего возможного количества электричества. Этот мельчайший заряд — “атом электричества” — соответствует по величине заряду электрона. Представление об атомистической природе электричества, согласно которому каждый электрический заряд составляет целое кратное от заряда электрона (е–) с тем или иным знаком, является в настоящее время общепринятым.

Первое определение заряда электрона было произведено в 1911 г., причём метод исследования основывался на наблюдении за поведением мельчайших капелек распылённого масла в электрическом поле. Если в пространство между двумя электродами ввести небольшое число таких капелек, то за каждой из них можно следить через снабжённый шкалой микроскоп.

Под действием силы тяжести капельки опускаются вниз тем быстрее, чем они тяжелее. Следовательно, по скорости падения можно вычислить вес любой отдельной капельки.

Если теперь направить в пространство между электродами пучок электронов, часть их задержится на капельках и тем самым сообщит последним отрицательный электрический заряд. При отсутствии поля это существенно не изменит поведения капелек, и они будут продолжать медленно падать. Напротив, сообщая верхней металлической пластине достаточный положительный, а нижней отрицательный заряд, можно не только приостановить падение, но и заставить заряженные капельки подниматься вверх.

Допустим, что при некоторой напряжённости поля между пластинами та или иная капелька не движется ни вверх, ни вниз. Это значит, что электрические силы в точности уравновешивают её вес. Зная напряжённость поля и вес капельки, можно рассчитать величину имеющегося на ней заряда.

Результаты многочисленных опытов при различных размерах капелек и напряжённостях поля неизменно показывали, что заряд всегда составляет целое кратное некоторого наименьшего или просто равен ему. Такое скачкообразное изменение заряда само по себе представляет наиболее убедительное доказательство атомистической природы электричества. Очевидно, что поглощение капелькой только одного электрона и должно обусловить наименьшую величину заряда, а поглощение двух, трёх и т. д. — соответствовать целым кратным от него. Наименьшая величина заряда и отвечает, следовательно, заряду электрона (1,591.10–19 Кл). Насколько эта величина мала, видно из того, что для создания силы тока в 1 А по проводу должно ежесекундно протекать 6,25.1018 электронов.

Летящий электрон отклоняется от прямолинейного пути и электрическим, и магнитным полями. Изучение характера этих отклонений позволило установить величину отношения заряда электрона к его массе (е/m). Зная заряд, можно было затем найти и массу электрона: она равна 9,11.10–31 кг. Радиус электрона оценивается в 0,2 пм.

Опыты с нагреванием и освещением металлов показывают, что наиболее легко удаляемыми частями атомной структуры являются именно электроны. Последние заряжены отрицательно, а атом в целом нейтрален; следовательно, внутри самого атома отрицательный заряд должен как-то компенсироваться положительным.

Учитывающая это модель была предложена Томсоном (1904 г.) на основе представления о положительном заряде, равномерно распределённом во всём объёме атома и нейтрализуемом электронами, вкрапленными в это “море положительного электричества”. Она не успела подвергнуться детальной разработке, так как была опровергнута работами Резерфорда.

Резерфорд проводил опыты с α-частицами. Масса каждой из них равна 4 единицам атомного веса (тогда как масса электрона составляет лишь 1/1820 такой единицы). Заряд их положителен и по абсолютной величине равен удвоенному заряду электрона. При радиоактивном распаде атома α-частицы вылетают с большой начальной скоростью.

Узкий пучок α-частиц направлялся на тонкий металлический листочек. Следить за их дальнейшим поведением можно было, передвигая по дуге приспособление, регистрирующее α-частицы. Оказалось, что большинство α-частиц проходит сквозь листочек без отклонения, часть отклоняется на различные углы, а некоторая ничтожная доля, примерно 1 частица на каждые 10000, отскакивает почти в обратном направлении. Результаты одного из опытов с рассеиванием α-частиц листочком золота приводятся ниже:

Угол отклонения. . . 15° 30° 45° 60° 75° 105° 120° 135° 150°

Число α-частиц . . . . 132000 7800 1435 477 211 70 52 43 33

Результаты этих опытов, особенно отскоки частиц обратно, невозможно истолковать на основе модели Томсона. В самом деле, летящая с большой скоростью и обладающая относительно большой массой при двойном положительном заряде α-частица может быть резко отброшена назад только в том случае, если она встретит на своём пути препятствие, обладающее большим, сконцентрированным в одном месте положительным зарядом. Распределённый по всему объёму положительный заряд таких отклонений дать не может.

Креме того, каждая α-частица на своём пути через металлический листок должна пройти сквозь множество атомов, а резкие отскоки наблюдаются лишь весьма редко. Это также заставляет предполагать, что пространство в атоме вовсе не сплошь заполнено положительным электричеством. На основании результатов опытов Резерфорда объём положительно заряженной части атома, его “ядра” оценивался примерно следующим образом. Если представить себе атом увеличенным до размеров шара с диаметром 10 м, то ядро имело бы размеры булавочной головки. Поэтому громадное большинство α-частиц и не отклоняется от прямолинейного пути, несмотря на то что каждая из них пролетает сквозь много тысяч атомов.

Диаметр атома металла составляет около 300 пм. При толщине металлического листочка в 0,1 мм (10-4 м) укладывается более 300 тыс. атомов.

Отклонения испытывают лишь α-частицы, пролетающие достаточно близко к ядру одного из встречаемых на пути атомов. При этом отскакивают обратно только те, которые прямо налетают на ядро. Подсчёт относительного числа таких отскоков и позволил оценить размеры ядра.

Опыты с α-частицами дали, однако, ещё больше — они позволили приблизительно оценить также и величину положительного заряда ядер различных атомов. В самом деле, отклонения α-частиц должны быть выражены тем сильнее, чем больше положительный заряд ярда. Результаты подсчётов показали, что этот заряд равняется наименьшему электрическому заряду (е), помноженному на число, соответствующее приблизительно половине атомного веса рассматриваемого элемента.

Основываясь на своих исследованиях, Резерфорд в 1911 г. предложил новую, “планетарную” модель, уподоблявшую атом солнечной системе. В центре должно находиться очень маленькое положительно заряженное ядро, заключающее в себе почти всю массу атома, а вокруг ядра — располагаться электроны, число которых определяется значением положительного ядра. Однако подобная система может быть устойчивой только в том случае, если электроны движутся, так как иначе они упали бы на ядро. Следовательно, электроны атома должны находиться приблизительно в таком же движении вокруг ядра, как планеты вокруг Солнца.

Правильность планетарной модели атома была вскоре подтверждена дальнейшими опытами с α- и β-частицами, пути которых стало возможным видеть и фотографировать благодаря разработанной в 1911 г. Вильсоном конденсационной камере. Принцип её действия основан на том, что при охлаждении насыщенного паром воздуха капельки тумана образуются почти исключительно вокруг посторонних частичек, особенно электрически заряженных. Конденсационная камера имеет сверху и частично с боков стеклянные стенки, а внизу поршень, при быстром выдвижении которого содержащийся в ней влажный воздух несколько охлаждается за счёт расширения. Если воздух был перед опытом тщательно освобождён от пыли, то образование тумана не наблюдается. Иначе обстоит дело при прохождении через камеру α- или β-частиц. И те и другие выбивают электроны из встречных молекул, создавая тем самым множество заряженных частиц. Вокруг последних тотчас образуются капельки тумана, ясно обозначающих весь пройденный α- или β-частицей путь.

Тяжёлая α-частица, выбивая из молекулы электрон, не изменяет своего прямолинейного движения; заметное отклонение её происходит лишь тогда, когда она пролетает вблизи ядра одного из атомов. Наоборот, лёгкая β-частица при выбивании электронов и сама изменяет свой путь (особенно, когда скорость её уменьшается). Обычным является прямолинейный путь, который заканчивается, когда скорость α-частицы уменьшается настолько, что она перестаёт выбивать электроны из встречных молекул.

Подсчёты показали, что β-частица пролетает в среднем сквозь 10 тыс. атомов, прежде чем выбивает электрон, а α-частица проходит сквозь 500 тыс. атомов, не подходя более двух или трёх раз к какому-нибудь ядру настолько близко, чтобы претерпеть заметное отклонение. Это убедительно доказывает, что ядра и электроны заполняют ничтожно малую часть занимаемого атомом пространства: фактический общий объём ядер всех атомов человеческого тела составляет лишь миллионную долю кубического миллиметра.

Атомные модели.

Планетарная модель атома имела большое принципиальное значение как новый и значительный шаг на пути познания внутренней структуры атома. Однако на первых порах она не могла выть уточнена, так как не было известно ни число, ни расположение электронов в атомах отдельных элементов.

Решение первого вопроса дали работы с так называемыми рентгеновскими лучами. В 1895 году Вильгельм Рентген изучая свойства катодных лучей, обнаружил, что те места стекляной трубки, на которые попадает поток электронов, испускает какое-то новое, действующее на фотографическую пластинку излучение, легко проходящее сквозь стекло, дерево и т. д., но сильно задерживаемое большинством металлов.

Исследование рентгеновских лучей показало, что они являются аналогичными видимому свету электромагнитными колебаниями, но характеризуются гораздо меньшими длинами волн (приблизительно 0,5-200 пм). В электромагнитном спектре рентгеновские лучи располагаются между ультрафиолетовыми и γ-лучами радия, частично налагаясь на последние.

Соответствующее отдельным областям электромагнитного спектра излучение различно поглащается земной атмосферой. Весьма важно существование “окна” для сантиметровых и метровых радиоволн. Оно прежде всего позводяет принимать отражение посылаемых с Земли радиоволн от различных небесных тел. Таким путём может быть, например, с недоступной ранее точностью определено расстояние до Луны (в среднем 384 тыс. км). Вместе с тем перед радиоастрономией открывается возможность регистрации собственного радиоизлучения, идущего из различных частей Вселенной.

Благодаря большой проникающей способности рентгеновские лучи широко применяются в медицине, так как позволяют путём просвечивания и фотографирования обнаружить внутри живого организма различные дефекты (переломы костей, опухоли и т. п. Очень “жёсткие” (т. е. характеризующиеся очень малой длиной волны) рентгеновские лучи применяются также для контрольного просвечивания металлического литья с целью обнаружения в нём внутренних пустот (“раковин”).

Рентгеновские лучи возникают при ударе быстро летящих электронов об атомы элементов, входящих в состав стекла. Если применять грубое сравнение, то это можно сопоставить с падением камня в спокойную жидкость — при таком ударе на её поверхности возникают волны. Характер последних будет при данной массе камня, его скорости, размерах и т. д. зависеть также и от свойств самой жидкости и изменится с заменой, например, воды на масло. Аналогично этому при данной скорости электрона характер рентгеновских лучей — их длина волны — будет меняться в зависимости от того, в атом какого элемента ударяется летящий электрон.

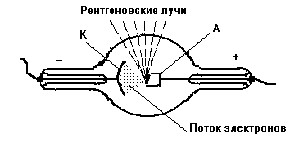
Рис. 1. Рентгеновская трубка.

Так как в состав стекла входят различные элементы, получаемое излучение содержит лучи различных длмн волн, что создаёт неудобства при пользовании им. Для избежания этого в рентгеновской трубке (рис. 1) против катода (К) устанавливается анод (А), сделанный из какого-дибо простого вещества. Попадая на его однородную поверхность, поток электронов вызывает образование рентгеновских лучей, характеризующихся некоторой определённой длиной волны.

В 1912 г. Мозли поставил перед собой задачу изучить длины волн рентгеновских лучей, получаемых от анодов, сделанных из различных химических элементов. Оказалось, что длины волн изменяются довольно закономерно, как это видно из рис. 2. При обработке результатов измерений обнаружилось, что корень квадратный из обратных значений длин волн является линейной функцией атомного номера, т. е. порядкового номера элемента в периодической системе (рис 3).

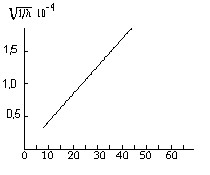
Рис. 2. Зависимость длин волн рентгеновского Рис. 3. Зависимость квадратного

излучения различных элементов от их корня из обратного значения

порядкового номера. длины волны излучения от порядкового номера элемента.

Наиболее надёжные результаты получаются при использовании жёстких рентгеновских лучей. Приметительно к ним уравнение Мозли имеет вид:

(1/λ)1/2 = α(Z - 1)

где λ - длина волны, Z - порядковый номер элемента в периодической системе и α - константа. Неизменность этой константы при переходе от одних элементов к другим и доказывает правильность найденного соотношения.

Теоретически следовало ожидать, что длина волны должна быть тем меньше (т. е. обратное её значение тем больше), чем больше заряд атомного ядра соответствующего элемента. Результаты опытов Резерфорда показали, что заряд ядра (Z в е-единицах) равняется приблизительно половине атомного веса. Но порядковый номер, по крайней мере для не очень тяжёлых атомов, приблизительно и равняется половине атомного веса. Всё это, вместе взятое, с очевидностью указывало на то, что положительный заряд ядра численно равен порядковому номеру элемента в периодической системе.

Таким образом, каждое ядро имеет следующие основные характеристики: заряд (Z) и массу (А). В настоящее время общепринято, что структурными составляющими всех атомных ядер (“нуклонами”) являются две более простые частицы с почти одинаковой атомной массой, близкой к 1 а.е.м. Одна из них протон (р) — несёт единицу положительного заряда, а другая — нейтрон (n) — электрически нейтральна. Структуру любого атомного ядра можно выразить простой формулой Zp + (A - Z)n, где А — округлённая до ближайшего целого числа масса атома в единицах атомных масс. Например, ядро атома фтора (Z = 9, A = 19) состоит из 9 протонов и 10 нейтронов.

У большинства химических элементов ядра отдельных атомов при постоянном числе протонов (Z) могут несколько различаться числом нейтронов (A - Z). Например, ядра атомов углерода всегда содержат 6 протонов, но нейтронов могут содержать либо 6, либо 7. Поэтому в природе существуют атомы углерода с массовым числом 12 (сокращённо 12С), и с массовым числом 13 (13С). Такие атомы одного и того же элемента, характеризующиеся различными массовыми числами (т. е. суммарным числом нуклонов), носят название изотопов данного элемента. Обычный углерод, имеющий атомный вес 12,011, представляет собой смесь 12С (около 98,9 %) и 13С (около 1,1 %). Химические свойства изотопов практически тождественны, состав их природной смеси при реакциях обычно не изменяется.

Атом в целом электронейтрален, т. к. число электронов, входящих в структуру электронной оболочки, равно заряду ядра, т. е. порядковому (атомному) номеру соответствующего химического элемента. Установление этого числа (Z) позволило перейти к построению атомных моделей.

В общих чертах вопрос был решён Бором (1913 г.). Для химии наиболее интересны модели, разработанные в 1916 г. Косселем. Хотя при их построении принимался во внимание ряд различных свойств атомов, здесь можно ограничиться рассмотрением химической стороны рассуждений.

При переходе от лёгких ко всё более тяжёлым атомам заряды их ядер последовательно возрастают. С другой стороны, химические свойства элементов при том же переходе меняются периодически. Отсюда следует, что химические свойства определяются не столько общим числом электронов в атоме, сколько их относительным расположением.

Но если это так, то и обратно исходя из химических свойств можно получить указание на расположение электронов. В частности, следует ожидать некоторую периодичность его изменения при последовательном возрастании зарядов ядер.

Интересно было, что при определённых условиях молекула, например, поваренной соли способна распадаться на натрий и хлор таким образом, что первый оказывается заряженным положительно, а второй отрицательно. Исследование этих частиц показывает, что заряд каждой из них численно равен заряду электрона. Происхождение обоих зарядов естественнее всего объяснить переходом одного электрона с атоманатрия на атом хлора. Но в поваренной соли и натрий и хлор одновалентны — из этого следует, что одна единица валентности отвечает одному переданному электрону. Тогда в случае, например, двухвалентного кальция можно ожидать перехода двух электронов. Действительно, опыт показавает, что получающаяся в тех же условиях частица кальция имеет два положительных заряда. Точно так же и в других случаях валентность элементов совпадает с числом передаваемых электронов. Такими легче всего передаваемыми — валентными — могут быть только электроны, наиболее удалённые от положительно заряженного атома.

Наконец, большую роль играли соображения, связанные со свойствами инертных газов: то лбстоятельство, что элементы этой группы не вступали в химические реакции, указывало на особую устойчивость электронных структур их атомов.

Построение простейшей модели атома водорода не представляет трудностей: электроно вращается в этом атоме вокруг протона. Для следующего элемента — гелия — возможны уже две различные модели (рис.4): два его электрона могут вращаться по орбитам, расположенным либо на различных расстояниях от ядра (А), либо на одинаковом, что схематически обозначено помещением их на одну окружность. Выбор между ними может быть произведён на основании химических свойств гелия. Если бы верна была модель А, то внешний электрон был бы связан в гелии не прочнее, чем в водороде. В соответствии с этим гелий должен был бы походить по свойствам на водород. Между тем он химически инертен. Это говорит за то, что оба его электрона находятся в одинаковых условиях и оба весьма прочно связаны с ядром, что и заставляет остановиться на модели Б.

Следующий элемент — литий —имеет уже три иэлектрона. Для него мыслимы четыре различные модели, коказанные на рис 5. Литий представляет собой металл, по химическим свойствам похожий на натрий и во всех своих соединениях одновалентный. Очевидно, что этому лучше всего соответствует модель Г. Принципиально важно то обстоятельство, что в ней сохраняется устойчивая конфигурация гелия из двух электронов в первом слое около ядра.

Элемент с атомным номером 4 — бериллий — всегда двухвалентен. Это показывает, что валентными являются в нём только два электрона, причём оба они находятся в одинаковых условиях. Очевидно, что и в бериллии сохраняется устойчивая гелийная двойка, а два остальных электрона располагаются в следующем слое.

Элемент № 5 — бор — трёхвалентен. Его модель, следовательно, строится аналогично модели бериллия, с той лишь разницей, что во втором от ядра слое содержится уже три электрона. Элемент № 6 — углерод — четырёхвалентен и расположение его электронов будет: 2 в первом слое и 4 во втором. Общая тенденция м развития атомных структур уже видна: при сохранении гелийной двойки в первом слое постепенно заполняется электронами второй. Это заполнение второго слоя будет, очевидно, продолжаться до тех пор, пока не достигнется число электронов, соответствующее его максимальной устойчивости. Но тогда должен получиться атом инертного газа. Рассматривая элементы, следующие в системе за углеродом, находим, что азот (2 и 5), кислород (2 и 6) и фтор (2 и 7) являются химически активными. Лишь элемент № 10 — неон — со структурой 2 и 8 оказывается аналогом гелия — инертным газом. Отсюда можно сделать вывод, что второй электронный слой становится устойчивым при 8 электронах.

Продолжая рассмотрение, находим, что элемент № 11 — натрий — одновалентен, магний — двухвалентен и т. д. Так как второй электронный слой заполнен уже в неоне, валентные электроны этих элементов будут располагаться в третьем слое.

Ввиду того, что пользование моделями атомов для выражения структур химических соединений затруднительно (с чисто графической стороны), обычно применяется упрощённый способ их изображения, при котором указывается только число электронов во внешнем слое:

Теория водородного атома

Вопрос о структуре простейшего атома — атома водорода — был разрешён в 1911 г. планетарной моделью, однако в самой этой модели таились внутренние противоречия. Действительно, по представлениям классической электродинамики вращающийся вокруг ядра электрон должен был непрерывно излучать энергию в виде электромагнитного излучения. Отсюда вытекали два важных следствия:

1. Из-за постоянного излучения энергии радиус орбиты электрона должен последовательно уменьшаться, в конце концов электрон должен упасть на ядро, что привело бы к уничтожению атомая. как такового.

2. Вследствие постепенного изменения скорости вращения электрона электромагнитное излучение атома должно состоять из непрерывного ряда лучей различных длин волн. Иначе говоря, спектр водорода может быть сплошным, т. е. содержать линии, соответствующие всевозможным длинам волн.

Ни то, ни другое следствие не оправдывается: самоуничтожения атомов водорода не происходит, а видимый спектр этого элемента со­стоит из ряда отдельных линий, соответствующих некоторым определенным длинам волн, как это видно из рис. III-21.

Голубой Фиолетовый

500 550 450 400 350 нм

Рис. Ill-21. Видимый спектр водорода (серия Бальмера).

Таким образом, либо планетарная модель, либо классическая тео­рия должна была быть неправильна. На самом деле в серьезных по­правках нуждались и та, и другая.

Еще до появления планетарной модели атома был отвергнут тезис классической электромагнитной теории света о непрерывности излуче­ния. «Тезису, гласящему, что скачков не бывает, а есть только н е п р е р ы в н о с т ь, с полным правом можно противопоставить а н т и- т е з и с, по смыслу которого в действительности и з м е н е н и е в с е г д а с о в е р ш а е т с я с к а ч к а м и, н о т о л ь к о р я д м е л к и х и б ы с т р о следующих один за другим скачков сливается для нас в один «непрерывный процесс» (Плеханов). Таким антите­зисом явилась квантовая теория (Планк, 1900 г.).

Согласно этой теории, энергия излучается не непрерывно, а опре­деленными порциями, являющимися кратными некоторого «кванта дей­ствия» (h). Величина излучаемого кванта энергии тем больше, чем больше частота колебаний излучения, т. е. чем меньше длина его волны. Например, фиолетовые лучи имеют бульшую энергию, чем красные. В электромагнитном спектре (рис. III-12) наибольшей энергией обладают γ-лучи, наименьшей — радиоволны. Величину кван­та энергии (E в Дж) для любого электромагнитного излучения можно вычислить из соотношения Е = hν, где h — квант действия (6,62·1034 Дж·с)и ν - частота колебаний рассматриваемого излуче­ния. Квантовая теория подтверждена обширным опытным материалом и является в настоящее время общепринятой.

1-2

Исходя из планетарных представлений и квантовой теории, Бор в 1913 г. построил модель атома водорода, не заключающую в себе тех противоречий, о которых говорилось выше. Модель эта была разрабо­тана на основе следующих положений.

1. Электрон может вращаться вокруг ядра не по всевозможным орбитам, а лишь по некоторым определенным. На таких «дозволенных» орбитах он вращается, н е и з л у ч а я э н е р г и и.

2. Ближайшая к ядру орбита соответствует наиболее устойчивому («н о р м а л ьл о м у») состоянию атома. При сообщении последнему энергии извне электрон может перейти на одну из более удаленных ор­бит, причем запас его энергии будет тем больше, чем дальше от ядра орбита, на которую он переходит, такой электрон находится на более высоком энергетическом уровне. Атом, содержащий электрон на одном из высоких энергети­ческих уровней, в отличие от нормального, называют «возбужден­ным». Как показывает опыт, обратный переход из возбужденного состояния в нормальное осуществляется весьма быстро: средняя «продолжительность жизни» большинства возбужденных атомов оценивается величинами порядка 10-8 сек.

3. Поглощение и излучение атомом энергии имеет место только при п е р е с к о к е электро­на с одной орбиты на другую. При этом разность энергий начального (Ео) и конечного (Ек) состояний воспринимается или отдается в виде кванта лучистой энергии (фотона), отвечающего излучению с частотой колебаний, определяемой рис. 111-22. Возможные соотношением hν = Eо - Eк.

Изложенные представления позволили вычислить радиусы различных «дозволенных» кван­товыми условиями орбит электрона в атоме водорода. Оказалось, что они относятся друг к другу как 12:22:32:42:...:n2. Величина n была названа г л а в н ы м к в а н т о в ы м ч и с л о м. Как видно из приведен­ного выше, n может принимать различные значения, соответствующие натуральному ряду целых чисел.

Радиус ближайшей к ядру орбиты (n = 1) оказался для водорода равным 53 пм. Электрон вращается по ней со скоростью около 2200 км/с (средняя скорость враще­ния Земли вокруг Солнца составляет 30 км/с). На рис. III-22 дана схема возможных для атома водорода орбит, причем приведены лишь первые четыре. Скорость вращения электрона на второй из них вдвое меньше, чем на второй из них вдвое меньше,чем на первой, на третьей — втрое меньше и т. д.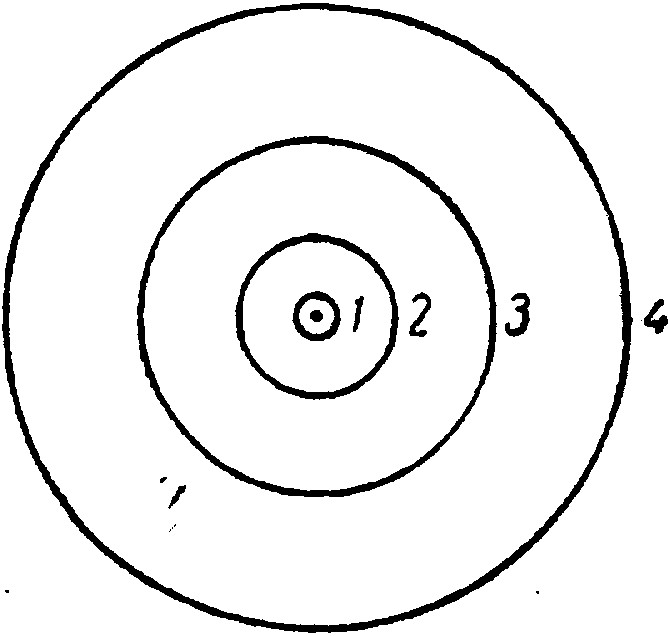

Рис. III-22. Возможные электронные орбиты атома водорода по Бору

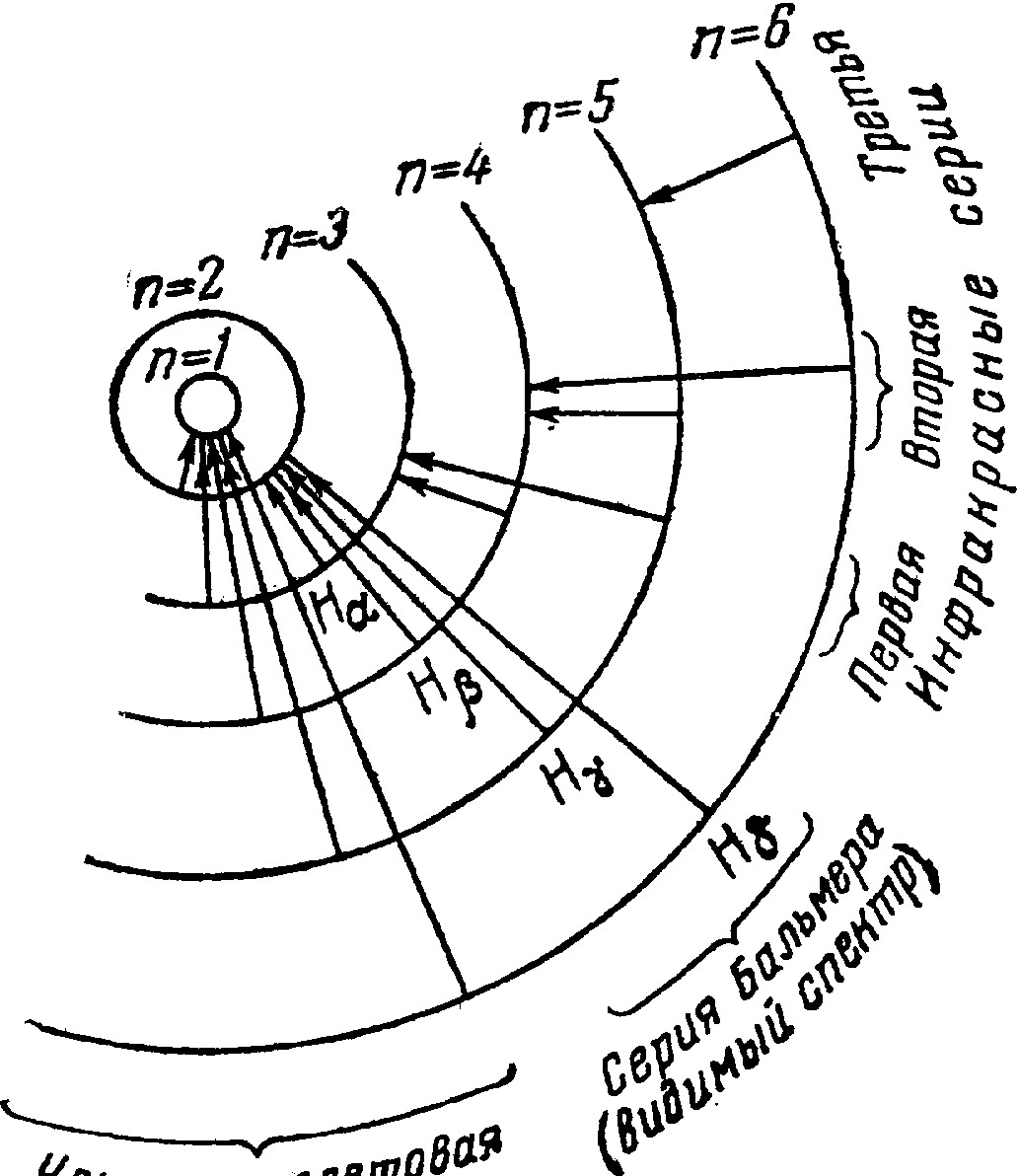
Рис. III-23. Схема происхождения водородного спектра

Работа, которую необходимо затра­тить для вырывания электрона водо­родного атома с той или иной орби­ты, обратно пропорциональна квадра­ту ее главного квантового числа. По­этому, например, вырвать электрон с третьей орбиты в девять раз легче, чем с первой.

Вычисленные частоты излучений, возникающих при перескоках электро­на с одних орбит на другие, оказались совпадающими с частотами линий на­блюдаемого на опыте водородного спектра. Как видно из рис. III-23, перескокам с различных более удаленных от ядра орбит на отвечаю­щую n = 1 соответствуют линии серии, лежащей в ультрафиолетовой области, перескокам на орбиту с n = 2— линии серии Бальмера (рис. III-21), а перескокам на орбиты с n = 3, 4 и 5 — линии трех серий, лежащих в инфракрасной области. Две последние серии были обнаружены экспериментально уже после разработки теории водород­ного атома и именно на основе ее предсказаний.

5-6

Если сообщить водородному атому достаточную энергию, то происходит его ионизация — распад на электрон и протон. Энергия, ко­торую нужно для этого затратить, отвечает n = ∞ (рис. III -24) и называется энергией ионизации (I). Она определена из спектра и для нормального состояния атома водорода составляет 1311 кДж на моль.

Н + 1311 кДж = Н+ + е

По соотношению I = 1311/n2 энергия ионизации мо­жет быть рассчитана и для возбужденных состояний атома водорода.

7

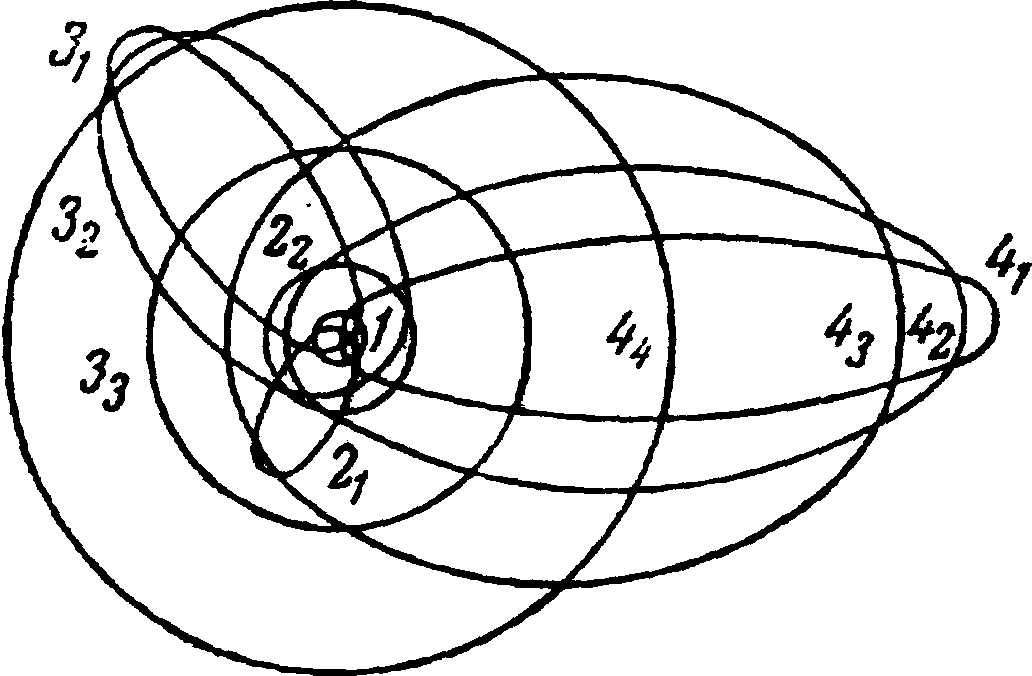
Дальнейшее развитие теории водородного атома было дано Зоммерфельдом (1916 г.), показавшим, что кроме круговых орбит электрон может двигаться и по эллиптическим (с ядром в одном из фокусов эллипса), причем почти одинаковому уровню энергии соответ­ствует столько возможных типов орбит, сколько еди­ниц в главном квантовом числе. Последнее определяет размер большой полуоси данного семейства эллипсов (в частном случае круга его радиус). Величина ма­лой полуоси определяется «п о б о ч н ы м» квантовым числом (6), которое также принимает значения по­следовательных целых чисел, но не может быть боль­ше главного.

Для большой полуоси эллипса действительно соот­ношение а = n2r, а для малой b = nkr, где r — радиус орбиты при нормальном состоянии атома (53 пм). На­пример, для главного квантового числа 3 возможны три типа эллипсов, характеризующиеся обозначениями 31, 32 и 33, которые показывают, что большая полуось относится к ма­лой соответственно как 3 : 1, 3 : 2 и 3 : 3. В последнем случае имеем частный вид эллипса — круг, который один только и рассматривался первоначальной теорией.

Модель возможных электронных орбит атома водорода по Зом- мерфельду показана на рис. III-25. Отвечающие каждой из них энергетические уровни (п о д у р о в н и) схематически сопоставлены на рис. III-26 (Б) с уровнями, соответствую­щими только круговым орбитам (Ф). Произведенное Зоммерфельдом уточ­нение модели водородного атома по­зволило объяснить тонкую структуру спектральных линий.

На рис. 111-26 видно, что наинизшие подуровни отвечают наиболее

**"У™ *** "Р*"™ Ри**Ш-25. Именно они и будут поэтому в первую тронных орбит атома водорода по

Зоммерфельду.

очередь заполняться электронами при построении нового слоя в м н о г о э л е-

ктронных атомах. Сами электронные слои (т. е. совокупности электронов с одинаковым значением главного квантового числа) в порядке удаления от ядра часто обозначаются буквами *, L, М, Л*, О, Р, Q.

У тяжелых атомов линии видимого спектра обусловливаются пере­скоками лишь самых внешних электронов, тогда как при перескоках в более глубоких слоях получаются линии, отвечающие ультрафиолето-

§ 4. "Теория водородного атома

вым или рентгеновским лучам. Энергия ионизации для этих атомов по­нимается как энергия, необходимая для удаления наименее прочно связанного электрона, каковым является один из занимающих самые внешние орбиты.*

Работу отрыва электрона от атома часто выражают путем указа­ния его ионизационного потенциала. Под последним понимается то ми­нимальное напряжение электрического поля в вольтах, при котором ускоряемый этим полем свободный электрон становится способным вызывать ионизацию данного атома (выбивая его внеш­ний электрон). Например, ионизационный потенциал атома водорода равен 13,595 е.

Ионизационному потенциалу численно равна энергия ионизации, измеряемая в электрон-вольтах (эе), а переход от них к тепловым единицам дается соотноше­нием: эв = 23,06 ккал/моль. Переводной ко­эффициент представляет собой энергию мо­ля (т. е. 6.02.10*) электронов, приобретае­мую им при прохождении ускоряющего поля с напряжением в 1 0. Таким обра­зом, работы ионизации атомов могут быть по желанию выражены и в тепловых еди­ницах (ккал/моль), и в электрон-вольтах (Э0).*

Рассмотренные выше представления не противоречат простейшим атомным моде­лям (рис. Ill-19), а лишь уточняют их. Дей­ствительно, распределение электронов по

А Б Рис. Ill-26. Схемы относитель­ных энергетических уровней круговых и эллиптических ор­бит.

слоям сохраняется в моделях Бора-Зоммерфельда и соответствует приводившемуся в предыдущем параграфе. И те, и другие модели, ко­нечно, не отображают структуру атомов во всей ее сложности. Несом­ненно, однако, что они все же дают правильное представление о некото­рых основных чертах этой структуры. Именно так и надо их понимать. «Признание теории снимком, приблизительной копией с объективной реальности, - в этом и состоит материализм» (Л е н и н). *-*

Дополнения

1) Числовая связь между значениями длин волн, частот колебаний и энергий электромагнитного излучения для видимой части спектра (4000-7000A) и ближай­ших к ней областей наглядно показана на рис. 111-27. В последней включены также наиболее употребительные в химии значения соответствующих энергий в ккал на грамм- атом (т. е. на 6,02«10** фотонов). Как легко установить по рис. 111-27, энергия излуче­ния на протяжении видимого спектра изменяется почти вдвое. '

2) При рассмотрении вопросов, связанных со спектрами, часто пользуются не непо­средственно длинами волн, а их обратными значениями - т. н. волновыми чис- л а м и' а) = т,, Так как длины волн при этом выражают в сантиметрах, ш имеет рязмерность см.-*. Волновое число показывает, сколько волн данной длины уклады­вается на протяжении 1 см. Взаимосвязь между энергией излучения и его волновым числом хорошо передается простым соотношением: Q = ю/350 ккал/е-атом. Подобное же соотношение Q== 1/350?* (где l, выражено в см) может быть использовано для приближенного расчета энергий излучения по длинам волн. Следует отметить, что вол­новые числа нередко называют «частотами» и обозначают через v. Это может повести

Ill. Основные представления о внутреннем строении вещества

к недоразумениям, так как в действительности v = (ri'c, где с - скорость света. Менее опасно в этом отношении также применяемое для волновых чисел обозначеяне v. Для сбозкачения см'* иногда вводят термин «кайзер» (К), а для 1000 cjh-*-«килокай- зср» (кК).

3) Условием равновесия в круговом движении является равенство сил центро­бежной и центростремительной. Для атома водорода первая из них определяется энер­гией движения электрона и радиусом окружности, по которой он вращается, вторая- электростатическим притяжением электрона к ядру. Если /я - масса электрона

Рис. Ill-27. Длины волн и анергий излучения.

(9,11•10-* г), е-его заряд (4,80-10-'° абсолютных электростатических единиц), r- радиус орбиты и и - скорость электрона, то условие равновесия для атома водорода выражается соотношением mv' e'

-"*"r*

Пмеп это одно уравнение с двумя неизвестными (и и r), еще нельзя сказать о внут­ренней структуре атома водорода ничего определенного.

5ор вышел из затруднения, приняв на основе представлений квантовой теории, что момент количества движения (тиг) электрона может изменяться лишь скач- к а к и в соответствии с уравнением

* * д (и== If 2) 3f...) *л,

1,054. 10--* эрг сек, -"' постоянную Планка - часто обозначают знач-

/ho2= -

2л,

Величину

ком и.

Сочетание введенного таким образом второго уравнения с предыдущим позво­ляет получить для обоих неизвестных параметров «движения электрона уже опреде- л е н н ы б общие решения:

h' 3 _ 2rte' 4л*е*/71 " h д

Подстановка в эти выражения известных значений констант (я, и, ё, т) приводит к следующим простым расчетным формулам для радиусов «дозволенных» орбит и скоро­стей вращения электрона:

т (А) == 0,53д' и о == -- км/сея

На орбите с д = 1 электрон совершает один оборот за время порядка К)-* сек.

4) Радиус первой электронной орбиты атома водорода входит в т. н. атомную си- cwmy единиц'. длины (0.53-10-® см), массы (9*10-* г), з9ряда (4,8.10-Ч' абс. ал. ед.), времени (2,42•10-'* сек), скорости (2,2«)(? см/сек), частоты (4,1.1016 сек-*), энергии (4,36.1011 эрг, или 27,2 за, вли 2*.108 сл-'* или 627,2 кк,ал1молъ). При рассмотрении атомных объектов в такой (преДложевной Харт- р и) системе единиц уравнения часто освобождаются от числовьш множителей и при­обретают более простой вид.

§ 4. Теория водородного атома

5) Потенциальная энергия двух численно равных разноименных зарядов е, на­ходящихся на расстоянии т друг от друга, определяется выражением --. С другой

стороны, кинетическая энергия *-g-* электрона в атоме водорода равн* •* (ср.

доп. 3). Так как общая энергия (Е) слагается из кинетической и потенциальной, для аточа водорода имеем * e' e' e'

Величина светового кванта (hv). отвечающего перескоку электрона в атоме водо­род? с одной орбиты на другую, определяется разностью энергий его начального (Ёа) и кснечного (Ек) состояний:

/м? == Ец - Ек == - -* + -* *'и. *'к.

*\**

Замена r его общим выражением (доп. 3) дает

*==**--*)

"* rl*r)

Подстановка значений констант приводит уравнение для частот колебаний к следую­щему расчетному виду:

v == 3,30 101* f-- - -*

*tt* п*н)

Наконец, соотношение *v = с (ср. 11 § 2) позволяет перейти от частот к длинам волн. Если выражать их в ангстремах, то расчетная форма уравнения приобретает вид:

*=*(*-*

Ниже в качестве .примера сопоставлены вычисленные по последней формуле и экспе­риментально определенные длины волн основных линий серии Бальмера (в ангстремах):

л™ Нд HP Hv на Теория: 6544 4848 4329 4091 Опыт; 6563 4861 4340 4102

Приведенное сопоставление показывает, что теория водор6дного атома даже в ее про­стейшей форме дает прекрасно согласующиеся с опытом результаты.

6) Сравнительно недавно инфракрасная часть водородного спектра была изучена более детально. Обнаружены две дополнительные линии первой серии и по одной во второй и третьей сериях. Впервые выявлена отвечающая перескоку электрона на ор­биту с п = 6 четвертая инфракрасная серия, представленная линией с длиной волны 123fi84A (т. е. уже более 0,01 мм). Энергия такого излучения составляет лишь 2,3 ккал/г-атом.

7) Приводившееся выше теоретическое выражение для /м? позволяет производить различные приближенные расчеты, связанные с изменением энергетического состояния атома водорода. Вводя в уравнение множитель 1,44•10*, служащий для перехода от эргов на один атом к /скал на грамм-атом, получаем

Пусть, например, требуется рассчитать энергии возбуждения, отвечай- щие линиям серии Бальмера (ив = 2). Подставляя в уравнение последовательно дв li= З* 4, 5, 6, получим:

Энергия возбуждения, ккал. » .

"а "р "v 44 59 66

70

tJ!. Основные представления о внутреннем строении вещества

Как рядно уже из приведенного ряда цифр, по мере удаления электрона от разница между энергиями последовательного возбуждения быстро уме шается. Этим и обусловлено наблюдающееся в спектре водорода быстрое сбл) ние отдельных линий при подходе к г р а н и ц е с е р и и (ср. рис. 111-21).

Сама подобная граница соответствует як = оо, т. е. полному отрыву элект* от ядра или ионизации атома. В зависимости отян соответствующие значе энергии будут, очевидно, различными. Наиболее важна из них энергия, отвечают н о р м а л ь н о м у исходному состоянию атома («н == 1), которая обычно и ука вар-тся под названием энергии ионизации. Экспериментальное ее определен из границы ультрафиолетовой серии приводит к значению 313,6 ккал, почти не от* чающемуся от вычисляемого по приведенной выше теоретической формуле (314 кка. Величина эта, под названием ридберг (Ry), иногда принимаемся за единицу энергг Она равна половине атомной единицы (доп. 4).

8) Для отрыва последнего электрона от атомного ядра с зарядом 1 требует. затратить в У раз больше энергии, чем для ионизации атома водорода. По расчеч на грамм-атом эта энергия равна 313,6 Z* ккал. Радиусы *-слоев в сложных атома относятся друг к другу, как обратные значения зарядов ядер, т. е. с возрастание, атомного номера элемента последовательно уменьшаются. Однако даже у наиболе тяжелых атомов они все еще в сотни раз превышают собственные размеры атомны. ядер.

9) Находящийся в электрическом поле электрон отталкивается от отрицатель­ного полюса и притягивается к положительному. Если f - разность потенциалов уско­ряющего поля (в б), то создаваемая им скорость электрона определяется соотноше­нием o=60fr*jF ка/сек. Следовательно, меняя напряжение, можно сообщать элек­трону определенные скорости, а тем самым и определенные величины кинетической энергии. Полезно запомнить следующее энергетическое соотношение между электрон- вольтами и волновыми числами (доп. 2): 1 эв = 8066 с.м-*.

10) Соотношение между числовыми значениями ионизационных потенциалов и энергий ионизации наглядно показано на рис. 111-28. Приводимыа в литературе зна­чения ионизационных потенциалов, как правило, относятся к О "К. Приближенный пере­счет соответствующих им энергий ионизации на 25°С может быть осуществлен путем

10 9 8 1 >t 1

5 4 3 ? fltlltlt ltfllllf 11 Ill t t t t 11 t I t I 111) t

Q I 300 250 200 W №0903070 60 'SO W 30 23кк!1л1мол{,

Рис. Ill-28. Ионизационные потенциалы и энергии ионизации.

добавления к приводимым значениям по 0,07 эв (или 1,5 ккал/моль) на каждый отрываемый электрон.

11) Ниже в качестве примера даются значения энергий ионп*а** ("i *l*i.*;* щих последовательному отрыву электронов из внешних электронных слоев атомов инертных газов. Главное квантовое число слоев указано при обозначении элемента.

Отрываемый электрон

Не (n=l) Ne (tt=2) Аг (п=5) Кг (rt=4) Хе (п=5) Rn (n=6)

24.581 21,559 15,755 13,996 12,127 10,746

54,403 41,07 27,62 24,56 21,2 *20.02)

63,5 40.90 36,9 32.1 (29,78)

97,02 59.79 (52,1) (45.46) (43,78)

126,3 75.0 (65,9) (56,9) (55,1)

157.91 91.3 (79,6) (68.3) (66,8)

(206.6) 124,0 (109,6) (96,0) (96,7)

ll*lt, (127,3) (110,4) (111.2)

Все цифры приводятся с тем числом знаков, которое отвечает предполагаемой точ­ности их определения из спектров или расчетным путем. Такие расчеты были произ­ведены почти для всех элементов. Результаты их, как менее надежные, здесь и далее даются в скобках.

§ 4. Теория водородного атома.

Рассмотрение приведенных данных показывает, что по мере роста главного кван­тового числа электронного слоя, т. е. удаления его от ядра, отрыв однотипного (на­пример, первого) электрона последовательно облегчается. Отрыв каждого последую­щего электрона из одного и того же слоя требует значительно большей затраты энер­гии, чем отрыв предыдущего. Особенно резкий скачок наблюдается при переходе от одного электронного слоя к другому. Например, энергия ионизации аргона, соответ* ствуюшая отрыву девятого электрона (т. е. первого из слоя с n == 2), составляет 421 эв, что почти в три раза превышает значение для восьмого электрона (т. е. последнего из слоя с п = 3).

12) Начиная с середины 20-х годов текущего века в развитии учения о строении атомов наметился перелом, обусловленный влиянием новой физической концепции (т. е. познавательной идеи), выдвинутой в *924 г. де-Бройлем..Если еще из самой квантовой теории вытекало и путем изучения столкновений фотонов с электронами было экспериментально подтверждено, что к а ж д а я э л е к т р о м а г н и т н а я волна одновременно обладает свойствами частицы, то, по де-Бройлю, имеет место и обратное: каждая

движущаяся частица одновременно обладает свойствами волны.

Количественную взаимозависимость между волновыми и корпускулярными (т. е. отве­чающими частицам) свойствами материи дает уравнение де-Бройля'.

l,»hinlv

17=J н»/

\*\*

*\

7.5 10 W /7=J h=Z

2.5 2.5 5 2.5 5 7.5 to и

Расстояние от ядра, *

где /I - квант действия, та - масса частицы, о - ее скорость и ?* - соответствующая длина йодны. Пользуясь этим уравнением, можно подсчитать массу кванта лучистой энергии

(u=c==3,00'10*'* см/сек), отвечающего любой длине волны. Вместе с тем можно вычислить длину волны, характерной для частицы с любой заданной массой и скоростью. Например, отвечающий линии Но, серии Бальмера (3*=6563A== 1-=6,563-10-* см) фотон имеет массу ftl=3.10--* а, т. е. он примерно в ЗООООО раз легче электрона. С другой стороны,, обладающий скоростью, например, G'K? см/сек электрон характеризуется волной с l* = 1,21 10-8 см = 1,21 А, т. е. волной типа рент­геновских лучей.

Это следствие теории вскоре нашло прямое экспериментальное подтверждение: оказзлось, что направленный на кристалл пучок электронов испытывает дифракцию подобно рентгеновским лучам. Немного позднее то же самое было установлено для атомов водорода и гелия. Так как дифракция является характерным свойством в о л н, приведенные результаты убедительно подтверждают правильность рассматриваемых представлений.

13) Развивавшаяся на базе этих представлений волновая механика подходит к во­просу о строении атомов с точки зрения характерного для нее принципа неоп- р е д е л е н н о с т и (Гейзенберг, 1925 г.). Согласно последнему характер движения электрона принципиально не может быть точно фиксирован. Модельное представление об атоме с его определенными орбитами электронов должно быть поэтому заме­нено описанием, при котором оценивается лишь вероятность нахождения элек­трона в том или ином месте пространства. Сама оценка этой вероятности производится хотя и с учетом структурных данных, но чисто математическим путем, при помощи т. н. волнового уравнения (Шредингер, 1926 г.). Последнее имеет характер постулата, истинность которого (в отличие от теоремы) устанавливается не выводом или прямым доказательством, а соответствием вытекающих из него следствий данным опыта.

Рис. 111-29 показывает распределение вероятностей нахождения электрона на том или ином расстоянии от ядра при различных квантовых состояниях атома водорода. Как видно из рисунка, при равенстве побочного и главного квантовых чисел (к == д)

Рис. Ill-29. Распределение вероятностей на­хождения электрона в атоме водорода.

Ill. Основные представления о внутреннем строении вещества

псложения м а к с и м а л ь н ы х вероятностей приблизительно соответствуют радиусам круговых орбит теории Бора-Зоммерфельда. Для эллиптических орбит («<я) на определенных расстояниях от ядра появляются уже не только максимумы, но и мини- мулн.? вероятности, т. е. в атоме образуются отдельные зоны с различной «плотностью электронного облака».

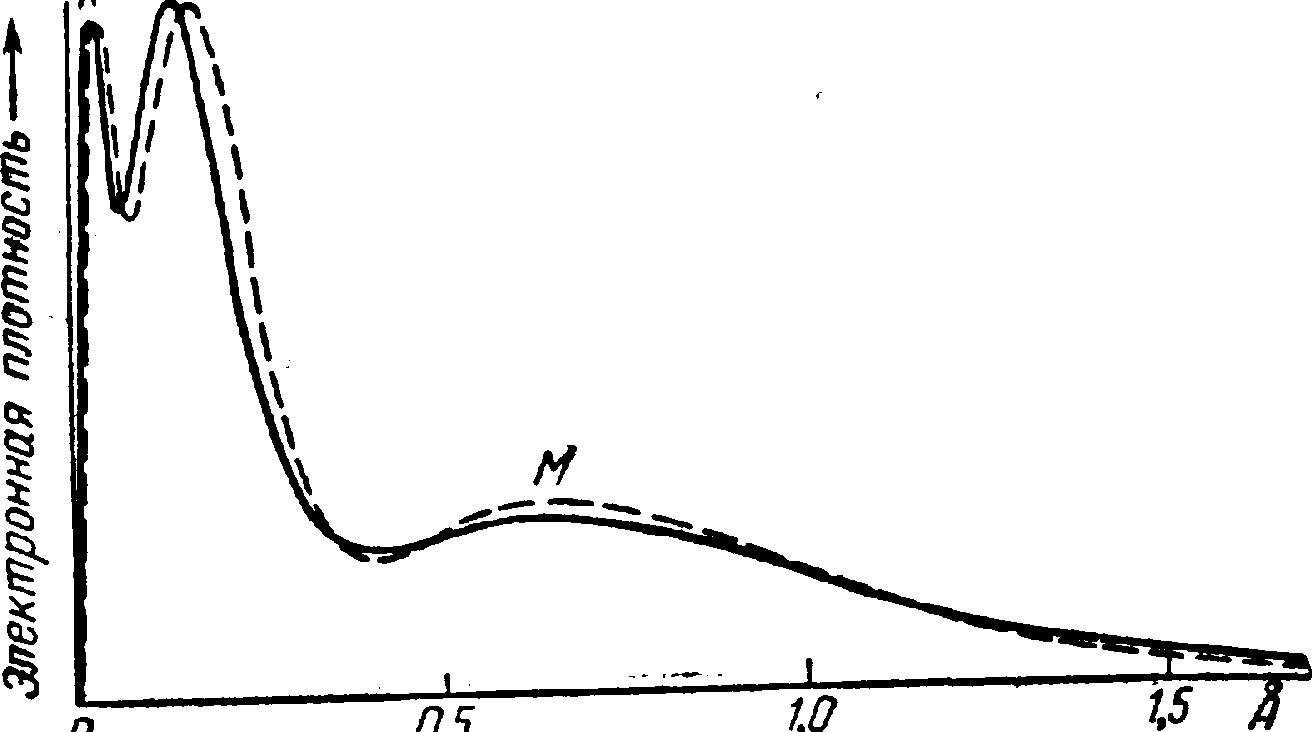
Подобный способ выражения вероятности нахождения электрона с помощью как бы «размазывания» его и оценки плотности получаемого т*им образом «электронного облака» особенно удобен, при волновомеханическом рассмотрении многоэлектронных ато­мов. Сплошная линия на рис. Ш-ЗО дает теоретически рассчитанное распределение элек- f тронной плотности для атома аргона. Как видно из рисунка, определен­ным электронным слоям (К, *-, М) теории Бора - Зоммерфельда отве­чают максимумы кривой. Однако значительная плотность электронного облака (т. е. вероятность нахожде­ния электрона) существует и м с ж д у слоями. Последние, таким образом, сколько-нибудь четко друг от друга не отграничиваются. Пунктиром по­казаны результаты проверки теорети­ческого распределения путем расчета электронной плотности на основе

экспериментальных данных по рассеиванию аргоном электронов. Как видно из ри­сунка, обе кривые практически совпадают.

Волновомеханический подход к атомным проблемам позволил разрешить ряд вопросов, остававшихся ранее неясными, а также получить некоторые количественные результаты со значительно большей точностью, чем удавалось раньше. Цингами харак­терный для волновой механики о т к а з о т н а г л я д н о с т и сильно снижает позна­вательную ценность этого метода и таит в себе опасность скатиться к такому миро­пониманию, при котором «..."материя исчезает", остаются одни уравнения» (Ленин).

14) Необходимо подчеркнуть, что волновая механика отнюдь не исключает корпу­скулярную трактовку явлений. Более того, сами ее уравнения основаны на представ­лении об электроне, как о точечном заряде, а не зарядовом облаке. «К волновому и корпускулярному описанию следует относиться как к равноправным н дополняющим друг друга точкам зрения на один и тот же объективный процесс.)* (Борн)-

Рис. Ill-30. Распределение электронной

в это* аргона.

§ 5. Валентная связь. Вопрос о природе сил, кота* .lbarot образование химических соединений, возникал еще в начале XIX века. Однако тогда он не мог быть удовлетворительно разрешен.*

Благодаря развитию наших знаний о строе­нии атомов мы теперь можем несколько ближе подойти к выяснению природы химического вза­имодействия и лежащих в его основе причин. * ___* При этом нужно, конечно, иметь в виду, что «че- Электроток jjiqiunflmqs

ловеческое понятие причины и следствия всегда

несколько упрощает объективную связь явлений природы» (Л е н и н) -

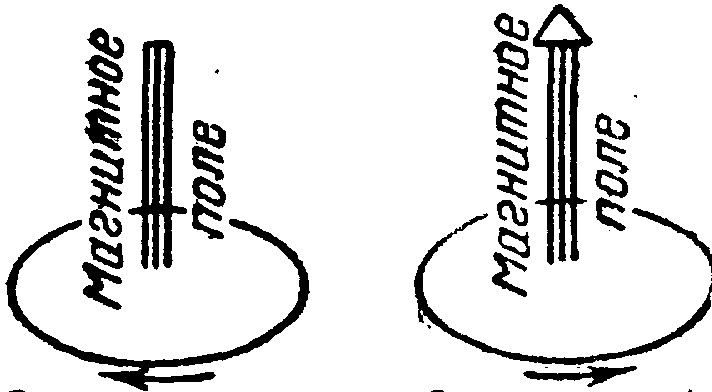
Как известно, протекающий по замкнутому контуру (как ранее считалось,-от плюса к ми­нусу) электрический ток создает магнитное поле, направленное в со­ответствии с «правилом буравчика» (рис. Ill-31). Аналогично (но с об­ратным направлением магнитного поля) ведет себя и вращающийся по орбите электрон. Вместе с тем имеет место и вращение его вокруг соб"

Рис. Ill-31. пр.***.* йу'

равчика,