Параллели с теорией поведения потребителя
С.Г.Светуньков
Теория поведения потребителя основана на ряде априорных предпосылок, о части из которых говорилось в начале параграфе Некоторые из этих предпосылок носят характер очень условный, гипотетический, хотя экономисты почему-то предпочитают говорить не о гипотезах, а об аксиомах. "Любое положение теории в большей или меньшей степени требует своего обоснования. Однако в действительности оказывается невозможным обойтись без определенной порции аксиоматики, что является отражением ограниченных возможностей познания..."(12, с.6).
Об аксиомах говорится и в одном из лучших, на мой взгляд, отечественных учебников по микроэкономике (2, с.111). Там в числе аксиом упоминается и такая, как "аксиома ненасыщения".
Напомню, что под аксиомой в какой-либо научной теории понимается исходное утверждение, которое берется в качестве недоказуемого утверждения в силу очевидности в данной теории и из которого выводятся все остальные предложения теории. Математики трактуют аксиомы четко: "аксиома - основное положение, самоочевидный принцип"(13, c.103).
Насколько самоочевидным является положение о том (аксиома ненасыщения), что "если набор А содержит не меньшее количество каждого товара, а одного из них больше, чем набор В, то А предпочтительнее В : Предполагается, что увеличение потребления любого товара - при фиксированных объемах потребления других товаров - улучает положение потребителя" (2, c.111-112) ? На мой взгляд, это вовсе не очевидно и, более того, возможно только для небольших объемов потребления товаров.
В этих же учебниках говорится о существовании "аксиомы насыщенности", которая полностью противоречит первой аксиоме. Очевидно, что если в науке имеется две аксиомы, полностью противоречащие друг другу, то эта ситуация свидетельствует как минимум о том, что одна из них не является аксиомой. Мне представляется, что более корректно в данном случае говорить о гипотезах, но не об аксиомах. Гипотеза носит предположительный характер, а аксиома - утвердительно безапелляционный.
Любой политэконом скажет, что основой теории поведения потребителей являются кривые безразличия и бюджетные линии. Для того, чтобы не утомлять читателя повторением уже известных истин напомню лишь самые важные положения, которые необходимы для проведения сравнительного анализа с положениями и выводами моей книги.
Кривая безразличия представляет собой множество точек на плоскости объемов двух товаров, каждая из которых представляет собой такой набор из двух товаров, что потребителю безразлично, какой из этих наборов выбрать (2, c.112-113).
Говорят о существовании кривых безразличия для совершенных заменителей; для взаимодополняющих товаров; для набора, в котором один из товаров имеет нулевую полезность для потребителя; для товаров, совместное потребление которых нежелательно; для блага и антиблага и тому подобное.
Этапность построений в теории потребительского поведения следующая.
В начале на плоскость с осями объемов товаров наносятся кривые безразличия. Затем на эту же плоскость наносят бюджетную линию, характеризующую тот доход потребителя, который тратится им на приобретение данных двух товаров. Набор товаров на бюджетной линии может быть различным, но главное условие заключается в том, что произведение приобретаемых объемов на цены товаров в сумме будут давать на каждой точке бюджетной линии одну и ту же величину, численно равную той части дохода, которая тратится потребителем на данные товары.
С увеличением дохода меняется бюджетная линия и место ее пересечения на графике с кривыми безразличия. Эти точки лежат на одной линии, которая характеризует объемы и пропорции потребления двух товаров в зависимости от доходов и называется <доход-потребление>
Подобным образом можно получить такой же результат, какой был мною получен с помощью методики эпюров. При этом, однако, надо учесть следующее.
Во-первых, для построения кривой "доход-потребление" следует вначале изобразить кривые безразличия, что не очень-то просто. Точки этих кривых представляют собой абстракцию и собрать данные по абстрактным представлениям очень сложно.
Во-вторых, приходится предполагать постоянство цен, иначе бюджетная линия будет "болтаться" по плоскости. Если же цены начинают меняться, то построение указанной кривой становиться делом невообразимо сложным, так как возникает необходимость прогнозирования цен. Часть этих случаев разбирается в литературе в разделах, посвященных эффектам замены и эффектам дохода по Хиксу и по Слуцкому.
Таким образом, стандартная классическая постановка задачи настолько сложна, что построить реальные кривые "доход-потребление" невозможно. Поэтому за этим разделом можно закрепить только теоретическую часть, выводы из которой могут быть полезны для практики. Это значит, что такая важная для практики зависимость, как кривая "доход-потребление", из теории поведения потребителя не выводится и не вычисляется.
Очевидно, что предлагаемый мной подход не только значительно проще, чем классический, но и позволяет при этом использовать все теоретически обоснованные построения в реальной практике - необходимо лишь собрать соответствующую статистику.
Цены двух товаров и зависимость от доходов
Спрос характеризуется двумя взаимосвязанными составляющими - ценой и объемом. В теории потребительского поведения рассматривается зависимость изменения объемов приобретения товаров от доходов потребителя. Как я не искал в научной литературе, мне так и не удалось найти другую, на мой взгляд, не менее важную составляющую - зависимость изменения цен приобретения товаров от доходов потребителя.
Для практикующего экономиста эта зависимость не менее важна, а для такого ее раздела, как маркетинг, еще более важна, чем зависимость изменения объемов приобретения товаров от доходов потребителя. Понятно при этом, что вряд ли удастся построить такую зависимость, используя методику классического подхода. В то же время методика построения эпюров, примененная в данной работе позволит это сделать без особых проблем.
Действительно, равновесная кривая в трехмерном пространстве имеет три проекции:
- на плоскость объем-доход;
- на плоскость цена- доход;
- на плоскость цена-объем.
Ранее я использовал проекции двух товаров на плоскости объем-доход и получил петли совместных распределений объемов товаров в зависимости от дохода. Ничто не мешает выполнить аналогичные построения с использованием других проекций, имеющих общую ось, а именно - проекций на плоскости цена-доход. При этом будет получено совместное распределение равновесных цен на два товара в зависимости от доходов у потребителей.
В предыдущей части этой книги я получил несколько видов проекций равновесной кривой на плоскость цена-доход. Так же, как и в случае распределения объемов в зависимости от дохода, здесь можно выделить два принципиально разных варианта.
Первый варианта - когда проекции двух товаров на их плоскости цена-доход полностью совпадают (при одинаковом масштабе цен), второй случай - когда проекции имеют разный характер.
Начну с первого случая, как наиболее простого для геометрических построений, но на практике маловероятного. Вновь прибегну к помощи методики построения эпюра. При этом две плоскости цена-доход представлены как две ортогональные плоскости трехмерного пространства цена товара А - цена товара Б - доход. Третьей ортогональной плоскостью данного пространства является плоскость цена товара А - цена товара Б. На рисунке 1 приведены эти две одинаковые проекции равновесных кривых товаров А и Б на плоскости цена-доход и показана процедура построения совместной проекции кривой равновесных цен на товары в зависимости от доходов потребителей.
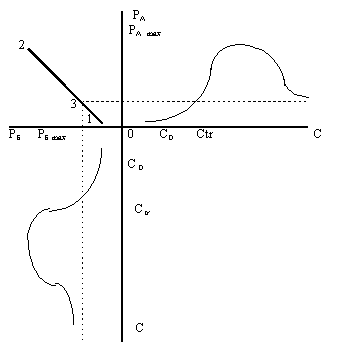
Рисунок 1. Эпюр кривой совместного распределения цен товаров в зависимости от дохода (невероятный случай)
В этом случае совместное распределение цен товаров в зависимости от доходов также будет лежать на отрезке прямой линии, причем начнется эта проекция из точки, обозначенной цифрой 1, не совпадающей с началом координат, своего максимума достигнет в точке 2, а закончится в точке 3. Все координаты полученной прямой равны друг другу. Отрезок прямой лежит под углом в 45 градусов к осям плоскости цен.
Очевидно, что если теперь менять отдельные характеристики проекций равновесных кривых на плоскости цена-доход (максимум, кривизну, минимумы и т.п.), то будет получено семейство кривых наподобие тех петель, которые были изображены в параграфе Принципиальное отличие заключается в том, что петли взаимного распределения цен никогда не закончатся на одной из осей плоскости. В том случае, когда приобретение одного из товаров начнется раньше, чем другого, кривая совместного распределения цен в зависимости от доходов сначала будет лежать на оси цен того товара, реализация которого началась раньше. Затем, при росте дохода начинается приобретение второго товара. При начале реализации второго товара кривая осуществит скачек перпендикулярно оси цен первого товара в точку с ценами первого товара и начальной ценой продаж второго товара. В дальнейшем кривые будут иметь характер, подобный кривым предыдущего параграфа.
Интересным представляется случай, который в параграфе 1.7 был назван третьим - когда производитель не в состоянии обеспечить потребителя товаром в достаточном количестве. В этом случае объемы товара становятся фиксированными, а с ростом доходов растут только цены, причем этот рост не ограничен ничем, кроме доходов потребителя. Для удобства дальнейших построений я перенесу эту проекцию в данный параграф и изображу ее на рисунке 2.
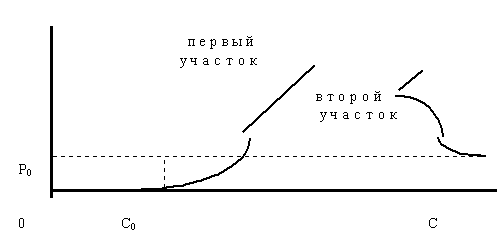
Рисунок 2. Вид проекции равновесной кривой на плоскость цена-доход при дефиците производства
Данная проекция имеет два участка - второй участок, как было показано в параграфе 1.7, крайне редко может встречаться на практике. Поэтому в моей работе я уделю внимание только первому участку.
Так, если попытаться найти совместное распределение на плоскости цен двух товаров, один из которых имеет проекцию вида первого участка рисунка 2, то будет получена очень интересная кривая. Конечно, конкретный вид кривой определяется характеристиками двух проекций - их кривизной, координатами точек перегиба, максимума и минимумов и тому подобное. Поэтому полученная кривая рисунка 3 носит условный характер, она демонстрирует лишь один из возможных случаев. В то же время возможное разнообразие кривых совместного распределения цен в зависимости от объемов с различными характеристиками проекций на плоскости цена-доход, будут все же иметь подобный же характер, составляя некоторое семейство кривых.
Пусть для определенности дефицит в объемах производства наблюдается для товара А. Товар Б является также товаром повседневного спроса, и его производство ничем не ограничено. Это приводит к тому, что равновесные цены и объемы последнего товара имеют ограничения при росте доходов у потребителя. Цены на первый товар не ограничены и растут вместе с ростом дохода у потребителя. Это означает, что на плоскости двух цен кривая совместного распределения цен двух товаров, при достижении некоторой точки, будет располагаться параллельно оси цен на товар А. Цены на товар Б при этом будут оставаться фиксированными при любой более высокой величине дохода.
Это означает, что все подобные проекции кривых совместного распределения цен в зависимости от доходов имеют ярко выраженную асимптоту, проходящую параллельно одной из осей цен того товара, объем производства которого дефицитен. Асимптота эта на другой оси цен будет равна цене этого товара при его рациональном потреблении. Полученная петля взаимного распределения цен товаров не имеет ограничений и является разомкнутой.
Если попытаться теперь построить проекцию двух товаров, имеющих проекции, подобные той, которая изображена на рисунке 2 (два товара дефицитны, и их дефицит снимается повышением цен), то будет получена в отличие от всех предыдущих построений не петля, а нелинейная кривая, стремящаяся с ростом доходов к прямой линии. Эта линия будет проходить под углом к осям координат. Ясно, что угол наклона этой прямой определяется углами наклона прямых двух проекций на плоскости цена-доход, которые возникают при постоянстве объемов и росте цен. В этом случае кривая не замыкается в петлю и имеет нелинейный характер в начальной и средней части своей проекции.
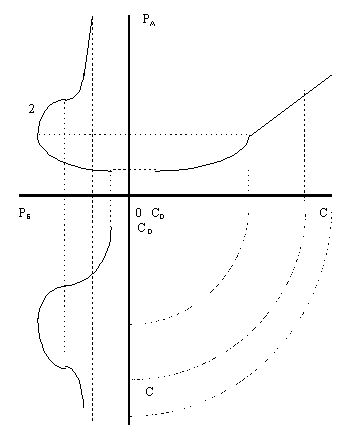
Рисунок 3. Эпюр кривой совместного распределения товаров, один из которых имеет проекцию, изображенную на рисунке 2
Таким образом, в отличие от кривых совместного распределения объемов товаров в зависимости от дохода, кривая совместного распределения цен может иметь три принципиально различных вида:
1) вид петли (обыкновенные товары);
2) вид кривой с вертикальной асимптотой (обыкновенный товар с дефицитным товаром);
3) вид кривой, стремящейся с увеличением доходов к наклонной асимптоте, уходящей в бесконечность (два дефицитных товара).
Завершая рассмотрение последних двух параграфов, отмечу, что, в принципе, можно построить петли взаимного распределения двух товаров от доходов потребителя достаточно оригинальным образом. Для одного товара можно рассмотреть проекцию равновесной кривой на плоскость цена-доход, для другого - на плоскость объем-доход. Полученное в результате использования эпюров распределение будет характеризовать изменение цены одного товара и объема другого товара от доходов потребителя. В настоящий момент я не знаю, как можно использовать подобные кривые. Вполне возможно, что и они могут пригодиться в экономической практике, например, при прогнозировании. Оставлю, однако, эту идею в данной работе без дальнейшего развития.
Для изображения на плоскости объемов множества доступных потребителю товарных наборов используют бюджетную линию (в многофакторном случае - бюджетную гиперплоскость). В общем виде она представляет собой сумму произведений неизвестного количества объема Qi каждого товара i на его известную цену Рi:
N
I = sum PiQi (1)
i = 0
Цена здесь выступает в качестве величины постоянной и характеризует углы наклона гиперплоскости (1) к ортогональным гиперплоскостям гиперпространства объемов.
Для того, чтобы нанести подобную же бюджетную линию (или гиперплоскость) на плоскость (или на гиперпространство) цен, следует зафиксировать объемы и в качестве переменных использовать цены товаров.
Предполагается, что расход покупателя - правая часть равенства (1) - полностью соответствует его доходу I - левая часть равенства. Очевидно, что это не так - экономическая теория давно оперирует таким понятием как "склонность к сбережению" (или накоплению), и это - не абстракция, а вполне реальное свойство. Поэтому корректнее будет вместо равенства (1) использовать неравенство:
N
I = sum PiQi (2)
i = 0
В любом случае правая часть указанных выражений представляет собой сумму расходов потребителя, которая ограничивается его доходами. Эта сумма расходов и представляет собой базу для расчета подавляющего большинства индексов.
Так, если указанную сумму расходов текущего периода разделить на аналогичную сумму расходов некоторого базового периода, получим индекс, называемый "индексом номинального дохода", который, как следует из неравенства (2), правильнее будет называть "индексом номинального расхода", хотя смена названий не меняет структуры самого показателя.
Теория индексов является очень развитым разделом науки. Еще в 1922 году И.Фишер опубликовал книгу, обобщающую не только всю известную к тому моменту совокупность индексов, но и определил возможные формулы индексов, исходя из механистического подхода - используя весь арсенал математических методов способом подстановок, получал различные формулы, в том числе и абсолютно абстрактные (14). Таким образом им были получены 134 различные формулы для расчета индексов. В дальнейшем теория индексов сменила свой количественный рост, выражавшийся в открытии новых индексов, на качественный - углубленное изучение уже имеющихся индексов. Появление новых индексов после 1922 года осуществляется относительно медленно. Теория индексов в настоящее время является хорошо разработанной и широко используется на практике.
Многообразие индексов определяется именно тем обстоятельством, что каждый из них имеет очевидные преимущества перед другими и не менее очевидные недостатки. В каждом конкретном случае оптимальным является какой-либо один индекс из всего множества возможных.
Практика, однако, показывает, что наиболее употребляемыми являются индексы Пааше и Ласпейреса. Индекс Пааше предполагает взвешивание цен по объемам их потребления в текущем периоде, а индекс Ласпейреса предполагает взвешивание цен двух периодов по объемам потребления в базисном периоде.
Индексы могут рассматриваться в качестве инструментов для измерения в общем случае двух объектов - цен того или иного рынка и состояния рынка в целом.
Если в первом случае еще можно говорить о более или менее успешном применении, то во втором случае об успехах говорить сложно. Практика показывает, что корреляция между конкретными значениями индексов и реальной ситуацией на рынке очень не велика. Тем более индексы оказываются непригодными в задаче предугадывания ситуации - они, в лучшем случае, способны подтвердить уже произошедшие изменения на рынке. Именно поэтому на фондовых рынках и происходят различного рода <черные> дни недели, когда происходят резкие обвалы. К тому же сами значения подобных индексов сложно интерпретируются, поэтому, как правило, о ситуации судят не по их абсолютным величинам, а по их относительной динамике (<упал> на столько-то пунктов, или <поднялся>).
Главная проблема этой части применения индексов, на мой взгляд, заключается в том, что индексы используются на несегментированных рынках. Предложенные в моей книге новые подходы позволяют говорить о возможности нового направления модификаций этого чрезвычайно важного раздела.
Как отмечает П.Кевеш (15, с.214), "в традиционной методологии статистической теории индексов неявно предполагается, что мы можем сравнивать физические объемы товарных масс даже при полностью изменившемся их составе".
Обоснование этого предположения зиждется на посылке о равенстве доходов потребителя его расходам (1). С учетом того, что это не так (2), индексы действительно плохо отражают существующую реальность. Как, однако, учесть то обстоятельство, что состав товаров непрерывно меняется, а в последние годы стремительного внедрения в жизнь достижений НТП это изменение вообще носит характер ускорения?
Найти ответ на этот вопрос можно, используя выводы, полученные мною ранее. На рисунке 1 изображены бюджетные линии и кривые безразличия.
Каждую кривую безразличия касается бюджетная линия (которая определяется доходом потребителя), точка их пересечения и есть оптимальный выбор потребителя.
Для каждой точки при фиксированном объеме, например точки 1, можно рассчитать совокупные стоимости (сложив произведения объемов товаров на их цены).
То же самое можно сделать и для других пар товаров, потребляемых индивидуумом с этим доходом. Если теперь суммировать полученные стоимости, будет получен агрегат, характеризующий суммарную стоимость потребления, - правая часть формулы 1.
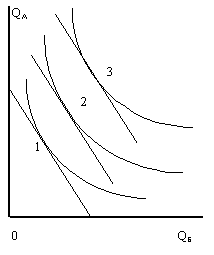
Рисунок 1. Кривые безразличия и бюджетные линии
Получаемые агрегаты и являются основанием для расчета различных индексов.
Следует обратить внимание на то, что в этом случае не только игнорируется возможное изменение номенклатуры товаров, на что указывал П. Кевеш, но и то, что покупки совершает один потребитель - абстрактный, совокупный один потребитель! Доходы этого потребителя предполагаются фиксированными и являются некоторой неизменной и единственной величиной. Легко заметить, что аналогичные расчеты можно сделать и для второй точки, характеризующей поведение индивидуума с более высокими доходами, для третьей и тому подобное.
Таким образом, формула 1 и различные производные от нее индексы исходят из двух предпосылок, которые принципиально не верны, а именно:
1) ситуация на рынке не зависит от номенклатуры товаров, а зависит от цен и объемов (стоимостей);
2) предполагается, что покупатели на рынке выступают не самостоятельно, сообразуясь со своими различными доходами и системами предпочтений, а как один покупатель с единственным усредненным доходом.
Что это означает в выводах моей работы?
На рисунке 2 изображена типичная петля распределения товаров, которые не являются предметами повседневного спроса (надеюсь, читатель согласится, что таких товаров - большинство). В зависимости от дохода потребителей объемы потребления этих двух товаров меняются. При незначительных доходах и при очень высоких доходах (сверхвысоких) эти объемы потребления равны нулю. При средних доходах пропорции их потребления также меняются с изменением величин этих доходов.
Для определенности сделаю следующие предположения. Пусть число потребителей, разделенных по уровню дохода в процентном отношении таково, как это показано на рисунке, - покупателей с низкими доходами - 10%, покупателей с малыми доходами - 15%, покупателей со средними доходами - 50%, покупателей с высокими доходами - 15%, покупателей со сверхвысокими доходами, не приобретающих данный товар, - нет.
Пусть в следующий момент доходы у всех этих категорий изменились на одну и ту же величину. Очевидно при этом, что их отношение к товарам изменилось.
Покупателей с низкими доходами нет (на рисунке 2 эти цифры обозначены в скобках), покупателей с малыми доходами - 10%, покупателей со средними доходами - 15%, покупателей с высокими доходами - 50%, покупателей со сверхвысокими доходами, не приобретающих данный товар, - 25%.
В результате этого изменения объемы приобретения двух товаров уменьшились, так же как уменьшаются (в общем случае) и равновесные цены на эти товары.
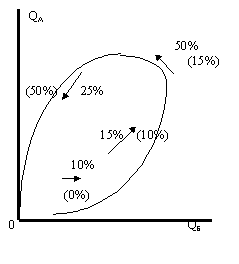
Рисунок 2. Одна из возможных петель распределения товаров, не являющихся предметом повседневного спроса
Если теперь суммировать произведения объемов приобретения данных двух товаров на соответствующие им цены, будет получена некоторая совокупная стоимость. В классической постановке в первом случае эта стоимость характеризует точку 1 на плоскости объемов товаров, во втором случае - точку 2 (рисунок 3).
Если теперь агрегаты отнести друг к другу получим элементарный индекс. Легко убедиться, что он будет меньше единицы. Индекс, таким образом, показывает на снижение стоимостей, а следовательно, на некоторые кризисные явления на рынке. И это в то время, когда доходы потребителей возросли и увеличилась покупательная способность потребителей. А это, согласитесь, движение рынка противоположное кризисному.
Очевидно, что для того, чтобы избежать подобной ситуации, в индекс следует включить траты на новые товары, которые до данного момента не приобретались. Однако <никто не может объять необъятное> - включить в совокупные расчеты данные по всем видам товаров и услуг не представляется возможным. Слишком обширен этот круг.
Впрочем, и это не всегда будет являться выходом из положения.
Рисунок 3. Агрегаты в первом и втором случаях рисунка 2 в классической постановке
Если вспомнить о склонности к сбережению с ростом доходов, то случай уменьшения индекса с ростом доходов вовсе не покажется маловероятным. Еще более вероятным такой случай окажется в случае расчета индексов на открытых рынках, когда покупатели со своими доходами могут перейти на другой рынок или прийти с других рынков.
Нет нужды доказывать, что использование более сложных индексов даст в этом случае аналогичные результаты. Расчеты на макроуровне будут в меньшей мере подвержены рассмотренной только что опасности - здесь проявляется эффект массовости и относительной автономности рынка на макроуровне.
Можно ли устранить причину появления недостатка в подобных случаях?
Для того, чтобы определить направление возможных модификаций индексов, следует определить зависимость стоимости приобретаемых товаров S qp от дохода потребителя. В том случае, когда склонности к накоплению нет вне зависимости от уровня дохода (при малых доходах), весь доход пускается на потребление (линия 1 рисунка 4). При этом выполняется равенство 1. В том же случае, когда с ростом дохода появляется все возрастающая склонность к накоплению (ломанная линия 2 рисунка 4), выполняется неравенство 2. Понятно, что в этом случае при расчете индекса следует придерживаться второй линии, используя первую лишь в качестве ориентира.
Что графически означает суммирование всех стоимостей по всем доходам?
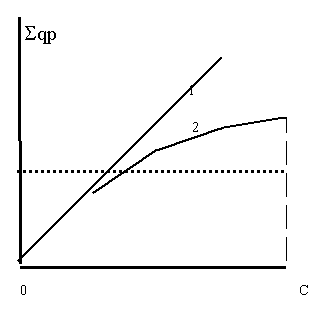
Рисунок 4. Зависимость совокупных стоимостей приобретаемых товаров от доходов
Как следует из рисунка, эта процедура имеет ясную геометрическую интерпретацию. Действительно, если полученную сумму (правая часть равенства 1) разделить на число слагаемых этой суммы, получится средняя стоимость приобретаемых всеми потребителями всех товаров. На рисунке 4 она изображена жирной пунктирной линией, параллельной оси доходов. Читатель, немного знакомый с теорией вероятностей и математической статистики, согласится со мной, что средняя в данном случае абсолютно неуместна - она выступает хорошей характеристикой как минимум тогда, когда описываемый ею процесс не имеет ярко выраженную динамику.
В данном случае зависимость стоимостей приобретаемого товара от дохода имеет ярко выраженную динамику к росту! Поэтому средняя арифметическая в данном случае абсолютно лишена какого-либо смысла. Она приемлема только как некоторая оценка истинного значения (в вероятностном случае - оценка математического ожидания).
Впрочем, саму среднюю арифметическую никто в теории индексов и не считает, а рассчитывают сумму стоимостей, которая в данном случае также неуместна, как и средняя арифметическая.
Что представляет собой расчет индекса номинального расхода?
После того, как рассчитывается сумма стоимостей для одного периода, таким же образом находятся суммы стоимостей в следующем периоде времени и отношение этих сумм будет давать нам искомый индекс. Читатель легко может убедиться в том, что та же самая величина будет получена, если вместо сумм стоимостей использовать их средние величины. Отношение двух неуместных величин вряд ли даст величину уместную.
Индексы Пааше и Ласпейреса обладают тем же самым свойством. Для того, чтобы придать индексам нормальный статистический смысл, следует сделать следующее.
Во-первых, необходимо разбить зависимость стоимостей от доходов на несколько отдельных участков в зависимости от доходов (рисунок 5) с тем, чтобы для этих сегментированных групп средняя стоимость уже была вполне уместной, логически оправданной, полностью и достоверно отражала наиболее общие свойства выделенного сегмента.
Для потребительского рынка на макроуровне, например, можно выделить следующие группы потребителей:
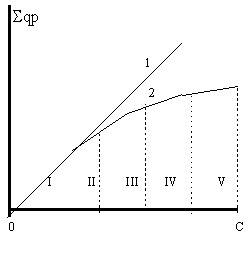
Рисунок 5. Зависимость совокупных стоимостей приобретаемых товаров от доходов
- с низкими доходами I;
- с малыми доходами II;
- со средними доходами III;
- с высокими доходами IV;
- со сверхвысокими доходами V.
Для каждой группы потребителей j (j= 1; 2; : 5) можно рассчитать сумму стоимостей, которая будет более корректна, нежели общая сумма для всех групп потребителей:
Ij = sum PiQi (3)
Эта корректность подтверждается уместностью использования в данном случае групповых средних арифметических. Теперь можно работать с полученными суммами и исчислять необходимые индексы в каждой из сегментированных групп. Единый обобщающий индекс, таким образом, становится малозначимым и его употребление на практике следует признать малоинформативным.
К тому же появляется возможность работы и с полученными стоимостями по группам с целью получения обобщающих характеристик, отражающих свойства экономической системы в целом. Можно, например, найти отношения между стоимостями каждой группы к суммарной стоимости:
I5/a I, I4/a I, I3/a I, I2/a I, I1/a I (4)
Эти отношения будут характеризовать реализацию покупательской способности каждой группы в общей совокупности, что может оказаться очень полезным в практике установления подоходного налога.
Если далее сравнивать эти отношения (4) с аналогичными расчетными величинами, но в следующий период времени, то можно получить ряд индексов, характеризующих динамику реализации покупательских способностей по каждой группе, что опять-таки следует признать очень информативным.
Подобные предложения можно развивать и далее - сравнивать друг с другом стоимости в различных сегментах по доходам, определять отношения стоимостей крайних групп и т.п.
Аналогичные подходы следует рекомендовать и для других рынков, не являющихся рынками макроуровня. Прежде, чем считать индексы, следует произвести сегментацию рынка, подвергаемого исследованию - только в этом случае индексы будут иметь явный смысл, заложенный в них теорией. В то же время известны случаи, когда на фондовых рынках рассчитывают индексы, в которые включают всю совокупность данных по всем объемам продаж и ценам продаж (если я не ошибаюсь, Нью-Йоркская фондовая биржа). Очевидно, что подобные индексы будут весьма условны и их ценность для практики мала. В этом случае также необходимо разбить котирующиеся ценные бумаги на группы по некоторым критериям сегментации, когда в сегментах будет получена однородная совокупность, характеризующаяся средними значениями стоимостей, например, в зависимости от капитала фирмы, выпустившей бумаги на рынок.