Элементы сферической геометрии
На протяжении многих веков человечество не переставало пополнять свои научные знания в той или иной области науки. Стереометрия, как наука о фигурах в пространстве, неотъемлемо связана со многими из научных дисциплин. К таким дисциплинам относятся: математика, физика, информатика и программирование, а также химия и биология. В последних стоит проблема изучения микромира, который представляет собой сложнейшую комбинацию различных частиц в пространстве относительно друг друга. В архитектуре постоянно используются теоремы и следствия из стереометрии.
Множество учёных геометров, да и простых людей, интересовались такой фигурой как шар и его «оболочкой», носящей название сфера. Удивительно, но шар является единственным телом, обладающим меньшей площадью поверхности при объёме, равном объёму других сравниваемых тел, таких как куб, призма или прочие всевозможные многогранники. С шарами мы имеем дело ежедневно. К примеру, почти каждый человек пользуется шариковый ручкой в конец стержня которой вмонтирован металлический шар, вращающийся под действием сил трения между ним и бумагой и в процессе поворота на своей поверхности шар «выносит» очередную порцию чернил. В автомобильной промышленности изготавливаются шаровые опоры, являющиеся очень важной деталью в автомобиле и обеспечивающей правильный поворот колёс и устойчивость машины на дороге. Элементы машин, самолётов, ракет, мотоциклов, снарядов, плавательных судов, подвергающиеся постоянным воздействиям воды или воздуха, преимущественно имеют какие либо сферические поверхности, называемые обтекателями.
Приращение знаний о шаре и сфере привело к возникновению нового раздела математики — сферической геометрии, в которой изучаются фигуры, расположенные на сфере. В своей работе постараюсь изложить основные элементы сферической геометрии, рассмотреть важнейшие закономерности в этой области знания.
Объектом работы является сферическая геометрия как один из разделов геометрии. Предмет работы — основные закономерности и особенности сферической геометрии.
Цель работы — выявить основные элементы сферической геометрии и описать важнейшие положения данной области научного знания.
Для осуществления цели необходимо решить ряд задач:
Охарактеризовать специфику сферической геометрии как области математики;
Определить основные понятия сферической геометрии;
Описать важнейшие положения сферической геометрии;
Рассмотреть особенности фигур, расположенных на сфере.
Структура работы обусловлена целью и задачами исследования. Работа состоит из введения, двух глав, разбитых на параграфы, заключения и списка литературы.
Глава 1. Шар и сфера
1.1. Шар и шаровая поверхность
Шаровой или сферической поверхностью называется геометрическое место точек пространства, удаленных от данной точки О (центра) на заданное расстояние R (радиус). Все пространство по отношению к данной шаровой поверхности разбивается на внутреннюю область (куда можно присоединить и точки самой поверхности) и внешнюю. Первая из этих областей называется шаром. Итак, шар — геометрическое место всех точек, удаленных от заданной точки О (центра) на расстояние, не превышающее данной величины R (радиуса). Шаровая поверхность является границей, отделяющей шар от окружающего пространства.
Шаровую поверхность и шар можно получить также, вращая окружность (круг) вокруг одного из диаметров.
Рассмотрим окружность с центром О и радиусом R (рис. 1), лежащую в плоскости λ. Будем вращать ее вокруг диаметра АВ. Тогда каждая из точек окружности, например М, в свою очередь опишет при вращении окружность, имеющую своим центром точку М0—проекцию вращающейся точки М на ось вращения АВ. Плоскость этой окружности перпендикулярна к оси вращения. Радиус ОМ, ведущий из центра исходной окружности в точку М, будет сохранять свою величину во все время вращения, и потому точка М все время будет находиться на сферической поверхности с центром О и радиусом R. Шаровая поверхность может быть получена вращением окружности вокруг любого из ее диаметров.
Сам шар как тело получается вращением круга; ясно, что для получения всего шара достаточно вращать полукруг около ограничивающего его диаметра.
Эти геометрические объекты, так же как окружность и круг, рассматривали еще в глубокой древности. Открытие шарообразности Земли, появление представлений о небесной сфере дали толчок к развитию специальной науки – сферики (сферическая геометрия), изучающей расположенные на сфере фигуры.
1.2. Сферическая геометрия
Сферическая геометрия - раздел математики, в котором изучаются фигуры, расположенные на сфере. Она представляет собой своеобразный мост между планиметрией и стереометрией, так как сферические многоугольники получаются в пересечении сферы с многогранными углами с вершинами в центре сферы, сферические окружности – в пересечении сферы с коническими поверхностями и т.д. Сферическая геометрия возникла в связи с потребностями астрономии. По-видимому, первым обращением человечества к тому, что потом получит название сферической геометрии, была планетарная теория греческого математика Евдокса (ок. 408–355гг. до н.э.), одного из учеников Академии Платона. Это была попытка объяснить движение планет вокруг Земли с помощью четырех вращающихся концентрических сфер, каждая из которых имела особую ось вращения с концами, закрепленными на охватывающей сфере, к которой, в свою очередь, были «прибиты» звезды. Таким образом объяснялись замысловатые траектории планет (в переводе с греческого «планета» – блуждающая). Именно благодаря такой модели древнегреческие ученые умели достаточно точно описывать и предсказывать движения планет. Это было необходимо, например, в мореплавании, а так же во многих других «земных» задачах, где нужно было учитывать, что Земля – не плоский блин, покоящийся на трех китах.
Значительный вклад в сферическую геометрию внес Менелай из Александрии жившего в 1 веке. Его труд Сферика стал вершиной достижений греков в этой области. В Сферике рассматриваются сферические треугольники – предмет, которого нет у Евклида. Менелай перенес на сферу евклидову теорию плоских треугольников и в числе прочего получил условие, при котором три точки на сторонах сферического треугольника или их продолжениях лежат на одной прямой. Соответствующая теорема для плоскости в то время была уже широко известна, однако в историю геометрии она вошла именно как теорема Менелая, причем, в отличие от Птолемея, у которого в работах немало вычислений, трактат Менелая геометричен строго в духе евклидовой традиции.
Таким образом, потребности человека в астрономических знаниях, привели к возникновению особой области математической науки — сферическая геометрия. Эта наука получила широкое распространение в настоящее время.
Глава 2. Элементы сферической геометрии
2.1. Основные положения сферической геометрии
Именно большим окружностям и отводится роль прямых в сферической геометрии. Как правило, через две точки на сфере, как и на плоскости, можно провести только одну сферическую прямую. Исключение составляют диаметрально противоположные точки: например, через полюсы на глобусе проходит бесконечно много меридианов. Всякая плоскость, пересекающая сферу, дает в сечении окружность. Если плоскость проходит через центр сферы, то в сечении получается так называемый большой круг. Через любые две точки на сфере, кроме диаметрально противоположных, можно провести единственный большой круг. (На глобусе примером большого круга служит экватор и все меридианы.) Через диаметрально противоположные точки проходит бесконечное количество больших кругов. Меньшая дуга AmB (рис. 2) большого круга является кратчайшей из всех линий на сфере, соединяющих заданные точки. Такая линия называется геодезической.
Рис.2
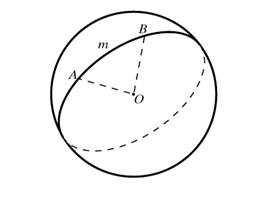
Геодезические линии играют на сфере ту же роль, что и прямые в планиметрии. Многие положения геометрии на плоскости справедливы и на сфере, но, в отличие от плоскости, две сферические прямые пересекаются в двух диаметрально противоположных точках. Таким образом, в сферической геометрии просто не существует понятия параллельности. Еще одно отличие – сферическая прямая замкнута, т.е. двигаясь по ней в одном и том же направлении, мы вернемся в исходную точку, точка не разбивает прямую на две части. Вот ещё удивление сферической геометрии: треугольник на сфере может иметь сразу три прямых угла, если, например, он ограничен двумя перпендикулярными меридианами и экватором.
Рис.3
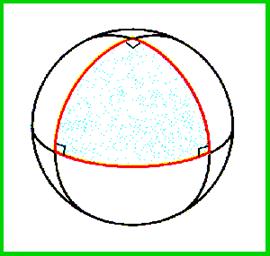
Теперь познакомимся с понятиями сферической геометрии. При этом мы будем постоянно сравнивать их с понятиями обычной геометрии.
2.2. Прямые, отрезки, расстояния и углы на сфере
Прямыми на сфере считаются большие окружности. Если две точки принадлежат большой окружности, то длина меньшей из дуг, соединяющих эти точки, определяется как сферическое расстояние между этими точками, а сама дуга – как сферический отрезок. Диаметрально противоположные точки соединены бесконечным числом сферических отрезков – больших полуокружностей. Длина сферического отрезка определяется через радианную меру центрального угла и радиус сферы R (рис. 4), по формуле длины дуги она равна R. Любая точка С сферического отрезка АВ разбивает его на два, и сумма их сферических длин, как и в планиметрии, равна длине всего отрезка, т.е. АОС + СОВ = АОВ. Для любой же точки D вне отрезка АВ имеет место «сферическое неравенство треугольника»: сумма сферических расстояний от D до А и от D до В больше АВ, т.е. AOD + DOB > AOB, – полное соответствие между сферической и плоской геометриями. Неравенство треугольника – одно из основополагающих в сферической геометрии, из него следует, что, как и в планиметрии, сферический отрезок короче любой сферической ломаной, а значит, и любой кривой на сфере, соединяющей его концы.
Рис.4
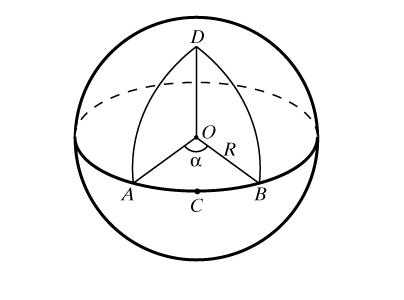
Таким же образом на сферу можно перенести и многие другие понятия планиметрии, в частности те, которые можно выразить через расстояния. Например, сферическая окружность – множество точек сферы, равноудаленных от заданной точки Р. Легко показать, что окружность лежит в плоскости, перпендикулярной диаметру сферы РР` (рис. 5), т.е. это обычная плоская окружность с центром на диаметре РР`. Но сферических центров у нее два: Р и Р`. Эти центры принято называть полюсами. Если обратиться к глобусу, то можно видеть, что идет речь именно о таких окружностях, как параллели, и сферическими центрами всех параллелей являются Северный и Южный полюса. Если диаметр сферической окружности равен /2, то сферическая окружность превращается в сферическую прямую. (На глобусе – экватор). В этом случае такую окружность называют полярой каждой из точек Р и P`.
Рис.5
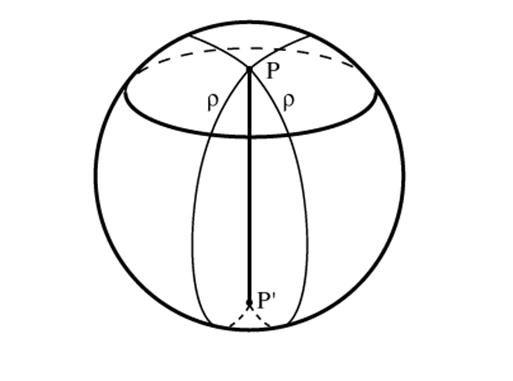
Одним из важнейших понятий в геометрии является равенство фигур. Фигуры считаются равными, если одну на другую можно отобразить таким образом (поворотом и переносом), что сохранятся расстояния. Это верно и для сферической геометрии.
Углы на сфере определяются следующим образом. При пересечении двух сферических прямых a и b на сфере образуются четыре сферических двуугольника, подобно тому, как две пересекающиеся прямые на плоскости разбивают ее на четыре плоских угла (рис. 6).
Рис.6
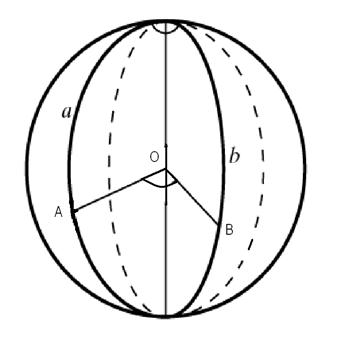
Каждому из двуугольников соответствует двугранный угол АОВ, образованный диаметральными плоскостями, содержащими a и b.
2.3. Сферический треугольник
Среди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Три больших окружности, пересекаясь попарно в двух точках, образуют на сфере восемь сферических треугольников. Зная элементы (стороны и углы) одного из них, можно определить элементы всех остальных, поэтому рассматривают соотношения между элементами одного из них, того, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла ОАВС, углы треугольника – двугранными углами того же трехгранного угла(1) (рис. 7).
рис. 7
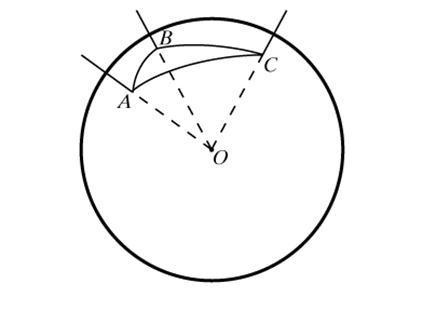
Многие свойства сферического треугольника (а они одновременно являются и свойствами трехгранных углов) почти полностью повторяют свойства обычного треугольника. Среди них – неравенство треугольника, которое на языке трехгранных углов гласит, что любой плоский угол трёхгранного угла меньше суммы двух других. Или, например, три признака равенства треугольников. Все планиметрические следствия упомянутых теорем вместе с их доказательствами остаются справедливыми на сфере. Так, множество точек, равноудаленных от концов отрезка, будет и на сфере перпендикулярной к нему прямой, проходящей через его середину, откуда следует, что серединные перпендикуляры к сторонам сферического треугольника AВС имеют общую точку, точнее, две диаметрально противоположные общие точки Р и Р`, являющиеся полюсами его единственной описанной окружности (рис. 8). В стереометрии это означает, что около любого трёхгранного угла можно описать конус. Легко перенести на сферу и теорему о том, что биссектрисы треугольника пересекаются в центре его вписанной окружности.
рис. 8
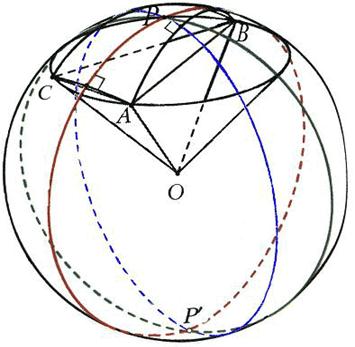
Теоремы о пересечении высот и медиан также остаются верными, но их обычные доказательства в планиметрии используют параллельность, которой, на сфере нет, и потому проще доказать их заново, на языке стереометрии. Рис. 9 иллюстрирует доказательство сферической теоремы о медианах: плоскости, содержащие медианы сферического треугольника АВС, пересекают плоский треугольник с теми же вершинами по его обычным медианам, следовательно, все они содержат радиус сферы, проходящий через точку пересечения плоских медиан. Конец радиуса и будет общей точкой трех «сферических» медиан.
Рис. 9
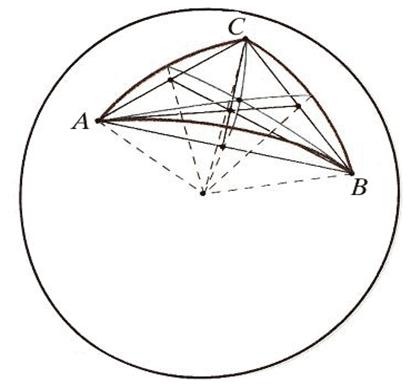
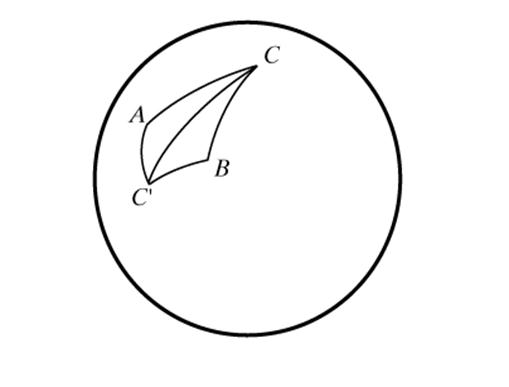
Свойства сферических треугольников во многом отличаются от свойств треугольников на плоскости. Так, к известным трем случаям равенства прямолинейных треугольников добавляется еще и четвертый: два треугольника АВС и А`В`С` равны, если равны соответственно три угла А = А`, В = В`, С = С`. Таким образом, на сфере не существует подобных треугольников, более того, в сферической геометрии нет самого понятия подобия, т.к. не существует преобразований, изменяющих все расстояния в одинаковое (не равное 1) число раз. Эти особенности связаны с нарушением евклидовой аксиомы о параллельных прямых и также присущи геометрии Лобачевского. Треугольники, имеющие равные элементы и различную ориентацию, называются симметричными, таковы, например, треугольники АС`С и ВСС` (рис. 10).
рис. 10
Сумма углов всякого сферического треугольника всегда больше 180. Разность А+В +С – = (измеряемая в радианах) – величина положительная и называется сферическим избытком данного сферического треугольника. Площадь сферического треугольника: S = R2 где R – радиус сферы, а – сферический избыток. Эта формула впервые была опубликована голландцем А.Жираром в 1629г. и названа его именем.
Каждая точка на сфере определяется заданием двух чисел; эти числа (координаты) определяются следующим образом (рис. 11). Фиксируется некоторый большой круг QQ` (экватор), одна из двух точек пересечения диаметра сферы PP`, перпендикулярного к плоскости экватора, с поверхностью сферы, например Р (полюс), и один из больших полукругов PAP`, выходящих из полюса (первый меридиан). Большие полукруги, выходящие из P, называются меридианами, малые круги, параллельные экватору, такие, как LL`, – параллелями. В качестве одной из координат точки M на сфере принимается угол = POM (высота точки), в качестве второй – угол = AON между первым меридианом и меридианом, проходящим через точку M (долгота точки, отсчитываемая против часовой стрелки).
рис. 11
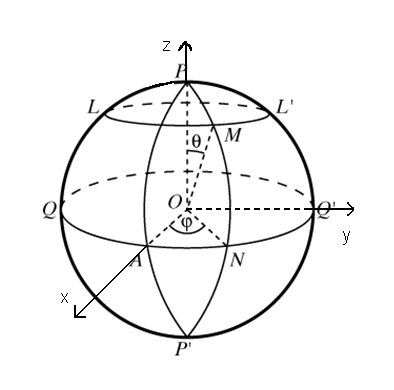
В географии (на глобусе) в качестве первого меридиана принято использовать Гринвичский меридиан, проходящий через главный зал Гринвичской обсерватории (Гринвич – городской округ Лондона), он разделяет Землю на Восточное и Западное полушария, соответственно и долгота бывает восточной либо западной и измеряется от 0 до 180° в обе стороны от Гринвича. А вместо высоты точки в географии принято использовать широту, т.е. угол NOM = 90° – , отсчитываемый от экватора. Т.к. экватор делит Землю на Северное и Южное полушария, то и широта бывает северной либо южной и изменяется от 0 до 90°. Сферические координаты с прямоугольными декартовыми координатами устанавливается следующими формулами: x = r sinсоsy = r sin sinz = r соs
2.5. Сферическая тригонометрия
Сферическая тригонометрия – раздел тригонометрии, в котором изучаются зависимости между величинами углов и длинами сторон треугольников, а также алгебраическими тождествами тригонометрических функций применительно к сферическим треугольникам. Применяется для решения различных геодезических и астрономических задач.
Пусть А, В, С - углы и а, b, с - противолежащие им стороны сферического треугольника ABC (рис.12 ). Углы и стороны сферического треугольника связаны следующими основными формулами Сферическая тригонометрия :
cos а = cos b cos с + sin b sin с cos А,
cos A = - cos B cos С + sin B sin С cos a,
sin a cos B = cos b sin c - sin b cos с cos А,
sin А cos b = cos B sin C + sin B cos С cos a;
рис.12
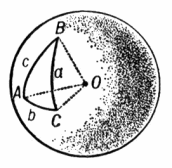
В этих формулах стороны а, b, с измеряются соответствующими центральными углами.
Для прямоугольных сферических треугольников (А = 90`, а - гипотенуза, b, с- катеты) формулы Сферической тригонометрии упрощаются, например:
sin b = sin a sin В,
cos a = cos b cos c,
sin a cos B = cos b sin c.
Формулы Сферической тригонометрии позволяют по любым трём элементам сферического треугольника определить три остальные (решить треугольник).
Рассмотренные элементы сферической геометрии дают нам обобщенное представление о данной области математической науки.
2.6. Применение сферической геометрии на практике
Сферическая геометрия нужна не только астрономам, штурманам морских кораблей, самолетов, космических кораблей, которые по звездам определяют свои координаты, но и строителям шахт, метрополитенов, тоннелей, а также геодезических съемках больших поверхностях земли, когда становится необходимым учитывать ее шарообразность.
Заключение
Подводя итоги проделанной работе, необходимо отметить, что в данной работе удалось: охарактеризовать специфику сферической геометрии как области математики на основе исторических фактов, определить основные понятия сферической геометрии, рассмотреть особенности фигур, расположенных на сфере, ознакомиться с главными учеными исследуемых сферическую геометрию в своих работах. Изучая особенности сферической геометрии, производилось сравнение с планиметрией и стереометрией.
Так же в работе было ознакомление, из каких потребностей возникла наука – сферическая геометрия, ее практическое применения в различных сферах знаний. Все это доказывает актуальность этого раздела математике в жизни человека.
Надеюсь, что и мне пригодятся эти знания при дальнейшем изучении геометрии в высшем учебном заведении.
Адамар Ж. Элементарная геометрия. – Ч.2.: Стереометрия : Пособие – 3-е изд. – М.: Учпедгиз, 1998.- 760 с.
АбрамовА.М, Виленкин Н.Я, ДорофеевГ.В, и др Избранные вопросы математики10 кл.: Факультативный курс./Под ред. ФирсоваВ.В/-М. : Просвещение 1992.
Александров.А.Д. и др.Геометрия для 10-11 классов Учебное пособие для учащихся школ и классов с углубленным изучением математики./А.Д. Александров, А.Л.Вернер, В.И.Рыжик. - 3-е изд., перераб.-М.: Просвещение, 1992.- 464с.
Атанасян Л.С. Геометрия: учебник для 10-11 классов средней школы.-М: Просвещение, 2007.- 208 с.
Гильберт Д. Кон-Фоссен С. Наглядная геометрия: Пер. с нем. – 3-е изд. – М.: Наука, 1981.- 344 с.
Глаголев Н. А. Проективная геометрия: Учеб. Пособие. – 2 –ое изд. испр. и доп. – М.: высш. школа, 1990. – 344 с.
Давидов А. Начала тригонометрии: 3-е изд., 1885.
Перепелкин Д. И. Курс элементарной геометрии. Ч II. Геометрия в пространстве: учеб. для пед. инст-ов. –М. Л.: гос. изд-во техн-теоретич. литер. 1992. – 333 с.
Саранцев Г.И. Упражнения в обучении математике.-М.:Просвещение, 1995.-240 с.
Стройк Д.Я. Краткий очерк истории математики, М., Наука, 1984 г.
Энциклопедический словарь юного математика/Сост. А.П.Савин.-М.: Педагогика, 1985.-352с., ил.
Энциклопедия элементарной математики кн. IV, V. /Под ред. В. И.Битюукова, И. Е, Морозовой, М.: Наука, 1966.- 624 с.
Для подготовки данной работы были использованы материалы с сайта http://referat.ru/