Избранные теоремы геометрии тетраэдра
Интерес к изучению тетраэдра возник у человечества с древних времен и не угасает до сих пор. Это связано не только с его красотой, но и с большой практической ценностью.
Тетраэдр является одним из основных фигур стереометрии, однако его изучение в курсе средней школы недостаточно подробно. В некоторых учебниках авторы избегают самой терминологии, предпочитая называть фигуру «треугольной пирамидой» (и рассматривают её именно в таком ключе), а об изучении различных видов тетраэдров зачастую и говорить не приходится.
Роль задач о тетраэдрах в математическом развитии школьников трудно переоценить. Они стимулируют накопление конкретных геометрических представлений, способствуют развитию пространственного мышления, что особенно важно в процессе изучения стереометрии.
Изучению тетраэдра как школе, так и в вузах посвящено лишь небольшое количество занятий, поэтому целью дипломной работы является изучение различных видов тетраэдров, а также теорем, связанных с геометрией тетраэдра. В соответствии с целью сформулированы следующие задачи:
1. Собрать сведения о тетраэдре из различных источников и привести их в систему; разобрать доказательства теорем, связанных с тетраэдром;
2. Проанализировать методику изложения материала в различных школьных учебниках;
3. Разработать курс занятий о тетраэдре для средней школы.
В первой главе моей дипломной работы речь пойдёт о различных видах тетраэдра и некоторых теоремах, касающихся этой фигуры. Вторая глава посвящена анализу учебного материала для средней школы по заданной теме и разработке курса занятий.
Глава I. Виды тетраэдров и теоремы о тетраэдрах
1.1 Теоремы о тетраэдрах
§1. Теорема Менелая
Теорема Менелая для треугольника.
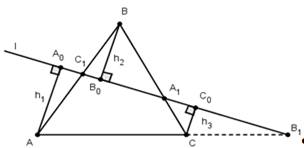
Пусть точки А1и С1 лежат на сторонах ВC и АC треугольника АВС, точка В1на продолжении стороны АС этого треугольника. Для того чтобы точки А1, В1, С1 лежали на одной прямой необходимо и достаточно, чтобы выполнялось равенство ![]() =
=![]() =
=![]() =1.
=1.
Доказательство.
Сначала докажем необходимость. Пусть точки А1,В1,С1 лежат на прямой l и AA0=h1, CC0=h3- перпендикуляры, опущенные соответственно из точек А, В, С на прямую l. Из подобия треугольников АА0С1и ВВ0С1получаем
![]() . Аналогично, рассматривая другие пары подобных треугольников, получаем
. Аналогично, рассматривая другие пары подобных треугольников, получаем ![]() ;
; ![]() . Перемножая полученные пропорции, приходим к требуемому равенству.
. Перемножая полученные пропорции, приходим к требуемому равенству.
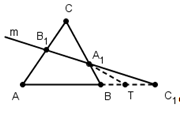
Теперь докажем достаточность. Пусть точки А1, В1, С1, лежащие на прямых ВС, АС, АВ таковы, что ![]() . Докажем, что точки А1, В1, С1 лежат на одной прямой.
. Докажем, что точки А1, В1, С1 лежат на одной прямой.
Проведем прямую А1В1и докажем, что точка С1 ей принадлежит. Предположим, что это не так. Сначала заметим, прямая А1В1не параллельна прямой АВ. Пусть Т - точка пересечения А1В1и АВ, тогда
![]() . Из условия и равенства (1) следует, что
. Из условия и равенства (1) следует, что ![]() . Так как точки Т и С1лежат вне отрезка АВ, их совпадение вытекает из следующей леммы.
. Так как точки Т и С1лежат вне отрезка АВ, их совпадение вытекает из следующей леммы.
Лемма 1.
Пусть А и В две различные точки, тогда для любого k>0, k≠1 на прямой АВ существуют две точки U и V такие, что ![]() , причем одна из этих точек принадлежит отрезку АВ, а другая лежит вне отрезка.
, причем одна из этих точек принадлежит отрезку АВ, а другая лежит вне отрезка.
Доказательство.
![]()
Введем на прямой АВ координаты, приняв точку А за начало координат. Пусть для определенности k>1, тогда координата искомой точки U, лежащей внутри отрезка АВ, удовлетворяет уравнению ![]() , откуда
, откуда ![]() . Точка V находится вне отрезка AB, из уравнения
. Точка V находится вне отрезка AB, из уравнения ![]() , откуда
, откуда ![]() . Случай 0
. Случай 0
Теорема Менелая допускает интересное стереометрическое обобщение.
Теорема Менелая для тетраэдра.
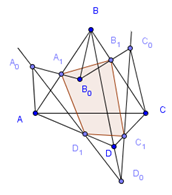
Если плоскость μ пересекает ребра АВ, ВС, CD и DA тетраэдра АВСD в точках А1, В1, С1, D1, то ![]() (2).
(2).
Обратно, если для четырех точек А1, В1, С1, D1,лежащих соответственно на ребрах АВ, ВС, СD, DA тетраэдра, выполнено равенство (2), то эти четыре точки лежат в одной плоскости.
Доказательство.
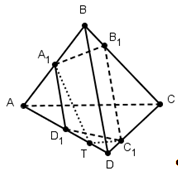
Пусть h1, h2, h3, h4- расстояния от точек А, В, С, D соответственно до плоскости μ, тогда ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Осталось перемножить полученные отношения.
Для доказательства обратной теоремы построим плоскость А1, В1, С1. Пусть эта плоскость пересекает ребро DA в точке Т.
По доказанному ![]() , а по условию
, а по условию ![]() , поэтому (и по лемме) точки Т и D1совпадают.Утверждение доказано.
, поэтому (и по лемме) точки Т и D1совпадают.Утверждение доказано.
§2. Теорема Чевы
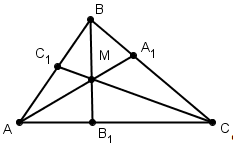
Теорема Чевы для треугольника.
Пусть точки А1, В1,С1лежат соответственно на сторонах ВС, АС и ВА треугольника АВС (см. рис). Для того чтобы отрезки АА1,ВВ1, СС1 пересекались в одной точке, необходимо и достаточно, чтобы выполнялось соотношение: ![]() (3) (отрезки АА1, ВВ1, СС1иногда называют чевианами).
(3) (отрезки АА1, ВВ1, СС1иногда называют чевианами).
Доказательство.
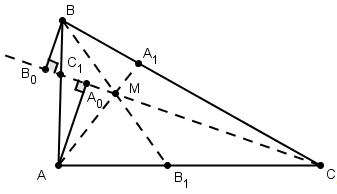
Необходимость. Пусть отрезки АА1, ВВ1, СС1пересекаются в точке М внутри треугольника АВС.
Обозначим через S1, S2, S3площади треугольников АМС, СМВ, АМВ, а через h1, h2 - расстояния от точек А и В до прямой МС. Тогда ![]() аналогично
аналогично ![]() ,
, ![]() . Перемножив полученные пропорции, убеждаемся в справедливости теоремы.
. Перемножив полученные пропорции, убеждаемся в справедливости теоремы.
Достаточность. Пусть точки А1, В1, С1лежат на сторонах ВС, СА, АС треугольника, и выполнено соотношение (3), М - точка пересечения отрезков АА1и ВВ1, а отрезок СМ пересекает сторону АВ в точке Q. Тогда, по уже доказанному ![]() ,
, ![]() . Из леммы снова следует совпадение точек Q=C1. Достаточность доказана.
. Из леммы снова следует совпадение точек Q=C1. Достаточность доказана.
Перейдем теперь к пространственному обобщению теоремы Чевы.
Теорема Чевы для тетраэдра.
Пусть М - точка внутри тетраэдра АВСD, а А1, В1, С1 и D1 - точки пересечения плоскостей СМD, AMD, АМВ и СМВ с ребрами АВ, ВC, СD и DA соответственно. Тогда ![]() (4). Обратно: если для точек
(4). Обратно: если для точек ![]() , то плоскости АВС, ВСD1 и DAB1проходят через одну точку.
, то плоскости АВС, ВСD1 и DAB1проходят через одну точку.
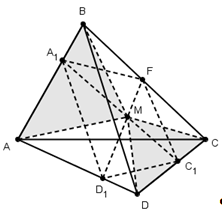
Доказательство.
Необходимость легко получить, если заметить, что точки А1, В1,С1, D1 лежат в одной плоскости (эта плоскость проходит через прямые А1С1 и В1D1, пересекающиеся в точке М), и применить теорему Менелая. Обратная теорема доказывается так же, так и обратная теореме Менелая в пространстве: нужно провести плоскость через точки А1, В1, С1 и доказать с помощью леммы, что эта плоскость пересечет ребро DA в точке D1.
§3. Свойства медиан и бимедиан тетраэдра
Медианой тетраэдра называется отрезок, соединяющий вершину тетраэдра с центром тяжести противоположной грани (точкой пересечения медиан).
Теорема (Применение теоремы Менелая).
Медианы тетраэдра пересекаются в одной точке. Эта точка делит каждую медиану в отношении 3:1, считая от вершины.
Доказательство.
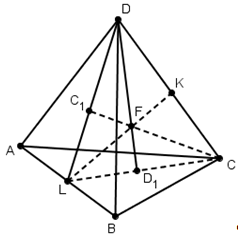
Проведем две медианы: DD1 и CC1 тетраэдра ABCD. Эти медианы пересекутся в точке F. CL – медиана грани ABC, DL – медиана грани ABD, а D1, C1 – центры тяжести грани ABC и ABD. По теореме Менелая: ![]() и
и ![]() . Запишем теорему для треугольника DLD1:
. Запишем теорему для треугольника DLD1: ![]() ;
; ![]() =>
=> ![]() Доказательство производится аналогично для любой другой пары медиан.
Доказательство производится аналогично для любой другой пары медиан.
Теорема (Применение теоремы Чевы).
Для начала дадим определения некоторых элементов тетраэдра. Отрезок, соединяющий середины скрещивающихся ребер тетраэдра называется бимедианой. Бивысотами (по аналогии) называют общие перпендикуляры скрещивающихся ребер.
Теорема.
Бимедианы тетраэдра пересекаются в той же самой точке, что и медианы тетраэдра.
Доказательство.
В треугольнике LDC отрезки DC и LF пересекутся в точке K. По теореме Чевы для этого треугольника: ![]() , т.е.
, т.е. ![]() , CK=KD, LK – бимедиана.
, CK=KD, LK – бимедиана.
Замечание 1.
FL=FK. Теорема Менелая для треугольника DLK: ![]() ,
, ![]() , отсюда LF=FK.
, отсюда LF=FK.
Замечание 2.
Точка F является центром тяжести тетраэдра. ![]() ,
, ![]() , значит
, значит ![]() .
.
1.2 Различные виды тетраэдров
§1. Пифагоровы тетраэдры
Треугольник называется пифагоровым, если у него один угол прямой, а отношение любых сторон рационально (т.е применяя подобие, можно из него получить прямоугольный треугольник с целыми длинами сторон).
По аналогии с этим, тетраэдр называют пифагоровым, если его плоские углы при одной из вершин прямые, а отношение любых двух ребер рационально (из него с помощью подобия можно получить тетраэдр с прямыми плоскими углами при одной из вершин и целыми длинами ребер).
Попробуем вывести "Уравнение пифагоровых тетраэдров", т.е. такое уравнение с тремя неизвестными ξ, η, ζ, что любой пифагоров тетраэдр дает рациональное решение этого уравнения, и наоборот, любое рациональное решение уравнения дает пифагоров тетраэдр.
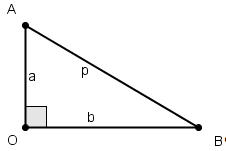
Сначала дадим способ описания всех пифагоровых треугольников.
На рисунке треугольник ОАВ - прямоугольный, длины его катетов обозначены через а и , а дина гипотенузы - через р. Число ![]() (1) условимся называть параметром прямоугольного треугольника ОАВ (или точнее, параметром "относительно катета а"). Используя соотношение р2=а2+b2, имеем:
(1) условимся называть параметром прямоугольного треугольника ОАВ (или точнее, параметром "относительно катета а"). Используя соотношение р2=а2+b2, имеем:
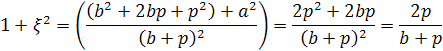
Из этих уравнений непосредственно получим формулы, выражающие отношения сторон прямоугольного треугольника через его параметр:
![]() и
и![]() (2).
(2).
Из формул (1) и (2) непосредственно вытекает следующее утверждение: для того, чтобы прямоугольный треугольник был пифагоровым, необходимо и достаточно, чтобы число ξ было рациональным. В самом деле, если треугольник пифагоров, то из (1) следует, что ξ рационально. Обратно, если ξ рационально, то согласно (2) отношения сторон рациональны, то есть треугольник пифагоров.
Пусть теперь ОАВС - тетраэдр, у которого плоские углы при вершине О прямые. Длины ребер, исходящих из вершины О, обозначим через a,b,с, а длины оставшихся ребер через р, q, r.
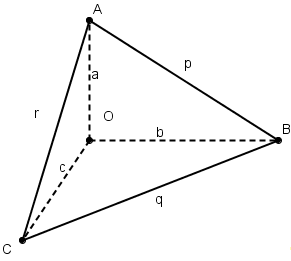
Рассмотрим параметры трех прямоугольных треугольников ОАВ, ОВС, ОСА:
![]() (3)
(3)
Тогда по формулам (2) можно выразить отношения сторон этих прямоугольных треугольников через их параметры:
![]() (4),
(4),
![]() (5).
(5).
Из (4) непосредственно вытекает, что параметры ξ, η, ζ, удовлетворяют соотношению ![]() (6). Это и есть общее уравнение пифагоровых тетраэдров.
(6). Это и есть общее уравнение пифагоровых тетраэдров.
Из формул (3) - (5) непосредственно вытекает следующее утверждение: для того чтобы тетраэдр ОАВС с прямыми плоскими углами при вершине О был пифагоровым, необходимо и достаточно, чтобы параметры ξ, η, ζ (удовлетворяющие уравнению (6)) были рациональными.
Продолжая аналогию пифагорова треугольника с пифагоровым тетраэдром, попробуем сформулировать и доказать пространственное обобщение теоремы Пифагора для прямоугольных тетраэдров, которая, очевидно, будет верна и для пифагоровых тетраэдров. В этом нам поможет следующая лемма.
Лемма 1.
Если площадь многоугольника равна S, то площадь его проекции на плоскость π равна ![]() , где φ - угол между плоскостью π и плоскостью многоугольника.
, где φ - угол между плоскостью π и плоскостью многоугольника.
Доказательство.
Утверждение леммы очевидно для треугольника, одна сторона которого параллельна линии пересечения плоскости π с плоскостью многоугольника. В самом деле, длина этой стороны при проекции не изменяется, а длина высоты, опущенной на нее при проекции, изменяется в cosφ раз.
Докажем теперь, что любой многогранник можно разделить на треугольники указанного вида.
Проведем для этого через все вершины многоугольника прямые, параллельные линии пересечения плоскостей, многоугольник разрежется при этом на треугольники и трапеции. Остается разрезать каждую трапецию по любой из ее диагоналей.
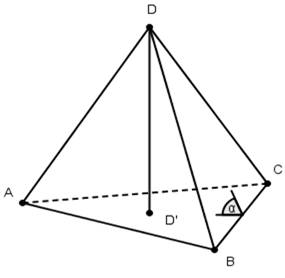
Теорема 1 (пространственная теорема Пифагора).
В прямоугольном тетраэдре АВСD, с плоскими углами при вершине D, сумма квадратов площадей трех его прямоугольных граней равна квадрату площади грани АВС.
Доказательство.
Пусть α - угол между плоскостями АВС и DВС, D' - проекция точки D на плоскость АВС. Тогда SΔDBC=СоsαSΔАBCи SΔD'BC=cоsαSΔDBC(по лемме 1), поэтому cоsα = ![]() .SΔD'BC=
.SΔD'BC= ![]() .
.
Аналогичные равенства можно получить и для треугольников D'АВ и D'АС. Складывая их и учитывая, что сумма площадей треугольников D'ВС, D'АС и D'АВ равна площади треугольника АВС, получаем требуемое.
Задача.
Пусть все плоские углы при вершине D прямые; a,,c – длины ребер, выходящих из вершины D на плоскость ABC. Тогда ![]()
Доказательство.
По теореме Пифагора для прямоугольного тетраэдра
![]() ;
; ![]()
![]()
![]() .
.
С другой стороны
![]()
![]() (:
(:![]()
1=![]() ) =>
) => ![]() .
.
§2. Ортоцентрические тетраэдры
В отличие от треугольника, высоты которого всегда пересекаются в одной точке - ортоцентре, не всякий тетраэдр обладает аналогичным свойством. Тетраэдр, высоты которого пересекаются в одной точке, называется ортоцентрическим. мы начнем изучение ортоцентрических тетраэдров с необходимых и достаточных условий ортоцентричности, каждое из которых можно принять за определение ортоцентрического тетраэдра.
(1) Высоты тетраэдра пересекаются в одной точке.
(2) Основания высот тетраэдра являются ортоцентрами граней.
(3) Каждые два противоположных ребра тетраэдра перпендикулярны.
(4) Суммы квадратов противоположных ребер тетраэдра равны.
(5) Отрезки, соединяющие середины противоположных ребер тетраэдра, равны.
(6) Произведения косинусов противоположных двугранных углов равны.
(7) Сумма квадратов площадей граней вчетверо меньше суммы квадратов произведений противоположных ребер.
Докажем некоторые из них.
Доказательство (3).
Пусть каждые два противоположных ребра тетраэдра перпендикулярны.
Следовательно, высоты тетраэдра попарно пересекаются. Если несколько прямых попарно пересекаются, то они лежат в одной плоскости или проходят через одну точку. В одной плоскости высоты тетраэдра лежать не могут, так как иначе в одной плоскости лежали бы и его вершины, поэтому они пересекаются в одной точке.
Вообще говоря, для того чтобы высоты тетраэдра пересекались в одной точке, необходимо и достаточно потребовать перпендикулярность только двух пар противоположных ребер. Доказательство этого предложения напрямую следует из следующей задачи.
Задача 1.
Дан произвольный тетраэдр ABCD. Докажите, что ![]() .
.
Решение.
Пусть а=![]() , b=
, b=![]() , с=
, с=![]() . Тогда
. Тогда ![]() ,
, ![]() и
и ![]() , складывая эти равенства, получаем требуемое.
, складывая эти равенства, получаем требуемое.
Далее докажем свойство (4).
Пусть а=![]() , b=
, b=![]() и с=
и с=![]() . Равенство
. Равенство![]() 2+
2+![]() 2=
2=![]() 2+
2+![]() 2, что
2, что![]() , т.е. (а,с)=0. Применяя данный алгоритм к другим парам противоположных ребер, очевидно, получим искомое утверждение.
, т.е. (а,с)=0. Применяя данный алгоритм к другим парам противоположных ребер, очевидно, получим искомое утверждение.
Приведем оказательство свойства (6).
Для доказательства используем следующие теоремы:
- Теорема синусов. «Произведение длин двух противоположных ребер тетраэдра, деленное на произведение синусов двугранных углов при этих ребрах, одно и то же для всех трех пар противоположных ребер тетраэдра».
- Теорема Бертшнейдера. «Если a и – длины двух скрещивающихся ребер тетраэдра, а ![]() - двугранные углы при этих ребрах, то величина
- двугранные углы при этих ребрах, то величина ![]() не зависит от выбора пары скрещивающихся ребер.
не зависит от выбора пары скрещивающихся ребер.
Воспользовавшись теоремой синусов для тетраэдра и теоремой Бертшнейдера, получаем, что произведения косинусов противоположных двугранных углов равны тогда и только тогда, когда равны суммы квадратов противоположных ребер, из чего и следует справедливость свойства (6) ортоцентрического тетраэдра.
В заключение пункта об ортоцентрическом тетраэдре решим несколько задач на эту тему.
Задача 2.
Докажите, что в ортоцентрическом тетраэдре выполняется соотношение ОН2=4R2-3d2, где О - центр описанной сферы, H - точка пересечения высот, R - радиус описанной сферы, d - расстояние между серединами противоположных ребер.
Решение.
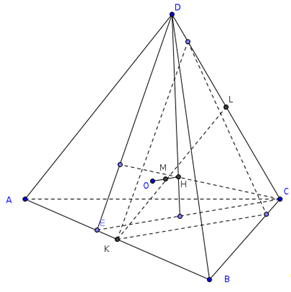
Пусть К и L - середины ребер АВ и СD соответственно. Точка Н лежитт в плоскости, проходящей через СD перепендикулярно АВ, а точка О - в плоскости, проходящей черех К перпендикулярно АВ.
Эти плоскости симметричны относительно центра масс тетраэдра - середины отрезка KL. Рассматривая такие плоскости для всех ребер, получаем, что точки Н и О симметричны относительно М, а значит КLМО - параллелограмм. Квадраты его сторон равны ![]() и
и ![]() , поэтому
, поэтому ![]() . Рассматривая сечение, проходящее через точку М параллельно АВ и СD, получаем что АВ2+CD2=4d2.
. Рассматривая сечение, проходящее через точку М параллельно АВ и СD, получаем что АВ2+CD2=4d2.
Здесь можно добавить, что прямую, на которой лежат точки О, М и Н, называют прямой Эйлера ортоцентрического тетраэдра.
Замечание.
Наряду с прямой Эйлера можно отметить существование сфер Эйлера для ортоцентрического тераэдра, о которых и пойдет речь в следующих задачах.
Задача 3.
Доказать, что для ортоцентрического тетраэдра окружности 9 точек каждой грани принадлежат одной сфере (сфере 24 точек). Для решения этой задачи необходимо доказать условие следующей задачи.
Задача 4.
Доказать, что середины сторон треугольника, основания высот и середины отрезков высот от вершин до точки их пересечения лежат на одной окружности - окружности 9 точек (Эйлер).
Доказательство.
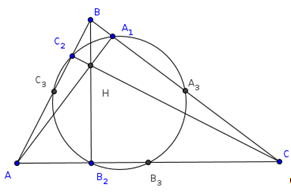
Пусть АВС - данный треугольник, Н - точка пересечения его высот, А1, В1, С1 - середины отрезков АН, ВН, СН; АА2 - высоты, А3 - середина ВС. Будем считать для удобства, что АВС - остроугольный треугольник. Поскольку ![]() В1А1С1=
В1А1С1=![]() ВАС и ΔВ1А2С1=ΔВ1НС1, то
ВАС и ΔВ1А2С1=ΔВ1НС1, то ![]() В1А2С1=
В1А2С1=![]() В1НС=180° -
В1НС=180° - ![]() В1А1С1, т.е. точки А1, В1, А2, С1лежат на одной окружности. Также легко увидеть, что
В1А1С1, т.е. точки А1, В1, А2, С1лежат на одной окружности. Также легко увидеть, что ![]() В1А3С1=
В1А3С1=![]() В1НС=180° -
В1НС=180° - ![]() В1А1С1, т.е. точки А1, В1, А3, С1тоже лежат на одной (а значит на той же) окружности. Отсюда следует, что все 9 точек, о которых говорится в условии, лежат на одной окружности. Случай тупоугольного треугольника АВС рассматривается аналогично.
В1А1С1, т.е. точки А1, В1, А3, С1тоже лежат на одной (а значит на той же) окружности. Отсюда следует, что все 9 точек, о которых говорится в условии, лежат на одной окружности. Случай тупоугольного треугольника АВС рассматривается аналогично.
Заметим, что окружность 9 точек гомотетична описанной окружности с центром в Н и коэффициентом ![]() (именно так расположены треугольники АВС и А1В1С1). С другой стороны, окружность 9 точек гомотетична описанной окружности с центром в точке пересечения медиан треугольника АВС и коэффициентом
(именно так расположены треугольники АВС и А1В1С1). С другой стороны, окружность 9 точек гомотетична описанной окружности с центром в точке пересечения медиан треугольника АВС и коэффициентом ![]() (именно так расположены треугольники АВС и треугольник с вершинами в серединах его сторон).
(именно так расположены треугольники АВС и треугольник с вершинами в серединах его сторон).
Теперь, после определения окружности 9 точек, можно перейти к доказательству условия задачи 3.
Доказательство.
Сечение ортоцентрического тетраэдра любой плоскостью, параллельной противоположным ребрам и проходящей на равном расстоянии от этих ребер, есть прямоугольник, диагонали которого равны расстоянию между серединами противоположных ребер тетраэдра ( все эти расстояния равны между собой, см. необходимое и достаточное условие ортоцентричности (5). Отсюда следует, что середины всех ребер ортоцентрического тетраэдра лежат на поверхности сферы, центр которой совпадает с центром тяжести данного тетраэдра, а диаметр равен расстоянию между серединами противоположных ребер тетраэдра. Значит, все четыре окружности 9 точек лежат на поверхности этой сферы.
Задача 5.
Доказать, что для ортоцентрического тетраэдра центры тяжести и точки пересечения высот граней, а также точки , делящие отрезки каждой высоты тетраэдра от вершины до точки пересечения высот в отношении 2:1, лежат на одной сфере ( сфере 12 точек).
Доказательство.
Пусть точки О, М и Н - соответственно центр описанного шара, ценетр тяжести и ортоцентр ортоцентрического тетраэдра; М - середина отрезка ОН (см. задачу 2). Центры тяжести граней тетраэдра служат вершинами тетраэдра, гомотетичного, с центром гомотетиии в точке М и коэффициентом ![]() , при этой гомотетии точка О перейдет в точку О1, расположенную на отрезке МН так, что
, при этой гомотетии точка О перейдет в точку О1, расположенную на отрезке МН так, что ![]() , О1 будет центром сферы проходящей через центры тяжестей граней.
, О1 будет центром сферы проходящей через центры тяжестей граней.
С другой стороны, точки, делящие отрезки высот тетраэдра от вершин до ортоцентра в отношении 2:1, служат вершинами тетраэдра, гомотетичного данному с центром гомотетии в Н и коэффициентом ![]() . При этой гомотетии точка О, как легко видеть, перейдет в ту же точку О1. Таким образом, восемь из двенадцати точек лежат на поверхности сферы с центром в О1 и радиусом, втрое меньшим, чем радиус сферы, описанной около тетраэдра.
. При этой гомотетии точка О, как легко видеть, перейдет в ту же точку О1. Таким образом, восемь из двенадцати точек лежат на поверхности сферы с центром в О1 и радиусом, втрое меньшим, чем радиус сферы, описанной около тетраэдра.
Докажем, что точки пересечения высот каждой грани лежат на поверхности той же сферы.
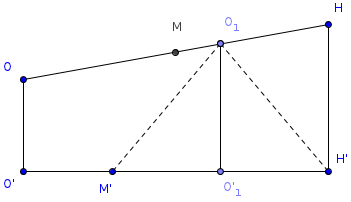
Пусть О`, Н` и М` - центр описанной окружности, точка пересечения высот и центр тяжести какой-либо грани. О` и Н` являются проекциями точек О и Н на плоскость этой грани, а отрезок М` делит отрезок О`Н` в отношении 1:2, считая от О`(известный планиметрический факт). Теперь легко убедиться (см. рис), что проекция О1 на плоскость этой грани - точка О`1 совпадает с серединой отрезка М`Н`, т.е. О1равноудалена от М` и Н`, что и требовалось.
§3. Каркасные тетраэдры
Каркасным называется тетраэдр, для которого существует сфера, касающаяся всех шести ребер тетраэдра. Не всякий тетраэдр каркасный. Например, легко понять, что нельзя построить сферу, касающуюся всех ребер равногранного тетраэдра, если его описанный параллелепипед "длинный".
Перечислим свойства каркасного тетраэдра.
(1) Существует сфера, касающаяся всех ребер тетраэдра.
(2) Суммы длин скрещивающихся ребер равны.
(3) Суммы двугранных углов при противоположных ребрах равны.
(4) Окружности, вписанные в грани, попарно касаются.
(5) Все четырехугольники, получающиеся на развертке тетраэдра, — описанные.
(6) Перпендикуляры, восстановленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.
Докажем несколько свойств каркасного тераэдра.
Доказательство (2).
Пусть О - центр сферы, касающейся четырех ребер во внутренних точках. заметим теперь, что если из точки Х провести касательные ХР и ХQ к сфере с центром О, то точки Р и Q симметричны относительно плоскости, проходящей прямую ХО и середину отрезка PQ, а значит плоскости РОХ и QОХ образуют с плоскостью ХРQ равные углы.
Проведем 4 плоскости, проходящие через точку О и рассматриваемые ребра тетраэдра. Они разбивают каждый из рассматриваемых двугранных углов на два двугранных угла. Выше было показано, что полученные двугранные углы, прилегающие к одной грани тетраэдра, равны. Как в одну, так и в другую рассматриваемую сумму двугранных углов входит по одному полученному углу для каждой грани тетраэдра. Проводя аналогичные рассуждения для других пар скрещивающихся ребер, получим справедливость свойства (2).
Вспомним некоторые свойства описанного четырехугольника:
a) Плоский четырехугольник будет описанным тогда и только тогда, когда суммы его противоположных сторон равны;
b) Если описанный четырехугольник разбить диагональю на два треугольника, то вписанные в треугольники окружности касаются
Учитывая эти свойства, легко доказать остальные свойства каркасного тетраэдра. Свойство (3) тетраэдра напрямую следует из свойства (b), а свойство (4) из свойства (a) и свойства (1) тетраэдра. Свойство (5) из свойства (3). Действительно, ведь окружности вписанные в грани тетраэдра, являются пересечениями его граней со сферой, касающейся ребер, откуда очевидно, что перпендикуляры, восстановленные в центрах вписанных в грани окружностей неминуемо пересекутся в центре этой сферы.
Задача 1.
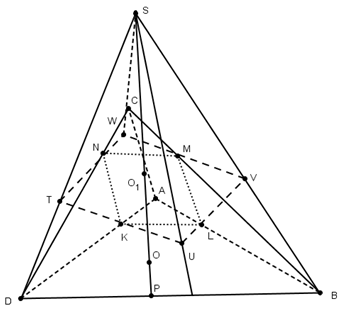
Сфера касается ребер АВ, ВС, СD и DA тетраэдра АВСD в точках L, M, N, K, являющихся вершинами квадрата. Докажите, что если эта сфера касается ребра АС, то она касается и ребра BD.
Решение.
По условия КLMN - квадрат. Проведем через точки К, L, M, N плоскости, касающиеся сферы. Т.к все эти плоскости одинаково наклонены к плоскости КLMN, то они пересекаются в одной точке S, расположенной на прямой ОО1, где - центр сферы, а О1- центр квадрата. Эти плоскости пересекают поверхность квадрата KLMN по квадрату TUVW, серединами сторон которого являются точки К, L, M, N. В четырехгранном угле STUVW с вершиной S все плоские углы равны, а точки К, L, M, N лежат на биссектрисах его плоских углов, причем SK=SL=SM=SN. Следовательно,
SA=SC и SD=SB, а значит АК=АL=CM=CN и ВL=BM=DN=DK. По условию АС тоже касается шара, поэтому АC=АК+CN=2АК. А так как SK - биссектриса угла DSA, то DK:КА=DS:SA=DВ:АС. Из равенства АС=2АК следует теперь, что DВ=2DK. Пусть Р - середина отрезка DВ, тогда Р лежит на прямой SO. Треугольники DOK и DOP равны, т.к. DK=DP и ![]() DКO=
DКO=![]() DPO=90°. Поэтому ОР=ОК=R, где R - радиус сферы, а значит, DB тоже касается сферы.
DPO=90°. Поэтому ОР=ОК=R, где R - радиус сферы, а значит, DB тоже касается сферы.
§4. Равногранные тетраэдры
Равногранным называется тетраэдр, все грани которого равны. Чтобы представить себе равногранный тетраэдр, возьмем произвольный остроугольный треугольник из бумаги, и будем сгибать его по средним линиям. Тогда три вершины сойдутся в одну точку, а половинки сторон сомкнутся, образуя боковые ребра тетраэдра.
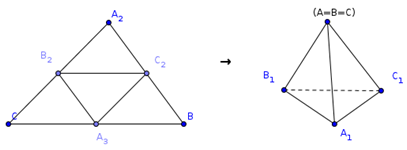
(0) Грани конгруэнтны.
(1) Скрещивающиеся ребра попарно равны.
(2) Трехгранные углы равны.
(3) Противолежащие двугранные углы равны.
(4) Два плоских угла, опирающихся на одно ребро, равны.
(5) Сумма плоских углов при каждой вершине равна 180°.
(6) Развертка тетраэдра - треугольник или параллелограмм.
(7) Описанный параллелепипед прямоугольный.
(8) Тетраэдр имеет три оси симметрии.
(9) Общие перпендикуляры скрещивающихся ребер попарно
перпендикулярны.
(10) Средние линии попарно перпендикулярны.
(11) Периметры граней равны.
(12) Площади граней равны.
(13) Высоты тетраэдра равны.
(14) Отрезки, соединяющие вершины с центрами тяжести противоположных граней, равны.
(15) Радиусы описанных около граней окружностей равны.
(16) Центр тяжести тетраэдра совпадает с центром описанной сферы.
(17) Центр тяжести совпадает с центром вписанной сферы.
(18) Центр описанной сферы совпадает с центром вписанной.
(19) Вписанная сфера касается граней в центрах описанных около этих
граней окружностей.
(20) Сумма внешних единичных нормалей (единичных векторов,
перпендикулярных к граням), равна нулю.
(21) Сумма всех двугранных углов равна нулю.
Практически все свойства равногранного тетраэдра следуют из его
определения, поэтому докажем только некоторые из них.
Доказательство (16).
Т.к. тетраэдр ABCD равногранный, то по свойству (1) AB=CD. Пусть точка К отрезка АВ, а точка L середина отрезка DC, отсюда отрезок KL бимедиана тетраэдра ABCD, откуда по свойствам медиан тетраэдра следует, что точка О - середина отрезка KL, является центром тяжести тетраэдра ABCD.
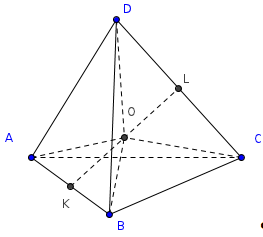
К тому же медианы тетраэдра пересекаются в центре тяжести, точке О, и делятся этой точкой в отношении 3:1, считая от вершины. Далее, учитывая вышесказанное и свойство (14) равногранного тетраэдра, получаем следующее равенство отрезков АО=ВО=СО=DО, из которого и следует, что точка О является центром описанной сферы (по определению описанной около многогранника сферы).
Обратно. Пусть К и L - середины ребер АВ и СD соответственно, точка О - центр описанной сферы тетраэдра, т.е. середина отрезка KL. Т.к. О - центр описанной сферы тетраэдра, то треугольники AOB и COD - равнобедренные с равными боковыми сторонами и равными медианами OK и OL. Поэтому ΔAOB=ΔCOD. А значит AB=CD. Аналогично доказывается равенство других пар противоположных ребер, из чего по свойству (1) равногранного тетраэдра и будет следовать искомое.
Доказательство (17).
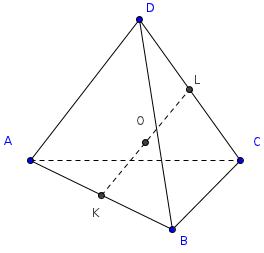
Рассмотрим биссектор двугранного угла при ребре AB, он разделит отрезок DC в отношении площадей граней ABD и ABC.
Т.к. тетраэдр ABCD равногранный, то по свойству (12) SΔABD=SΔABD=>DL=LС, откуда следует, что биссектор ABL содержит бимедиану KL. Применяя аналогичные рассуждения для остальных двугранных углов, и принимая во внимание тот факт, что биссекторы тетраэдра пересекаются в одной точке, которая является центром вписанной сферы, получаем, что эта точка неминуемо будет центром тяжести данного равногранного тетраэдра.
Обратно. Из того, что центр тяжести и центр вписанной сферы совпадают имеем следующее: DL=LC=>SABD=SADC. Доказывая подобным образом равновеликость всех граней и, применяя свойство (12) равногранного тетраэдра, получаем искомое.
Теперь докажем свойство (20). Для этого сначала нужно доказать одно из свойств произвольного тетраэдра.
тетраэдр теорема школьный учебник
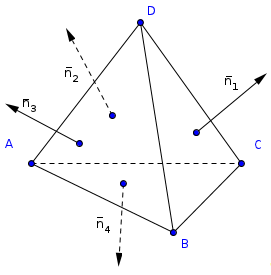
Лемма 1.
Если длины векторов перпендикулярных к граням тетраэдра численно равны площадям соответствующих граней, то сумма этих векторов равна нулю.
Доказательство.
Пусть Х - точка внутр и многогранника, hi (i=1,2,3,4) - расстояние от нее до плоскости i-ой грани.
Разрежем многогранник на пирамиды с вершиной Х, основаниями которых служат его грани. Объем тетраэдра V равен сумме объемов этих пирамид, т.е. 3 V=∑hiSi, где Siплощадь i-ой грани. Пусть далее, ni- единичный вектор внешней нормали к i-ой грани, Mi - произвольная точка этой грани. Тогда hi =(ХMi, Sini), поэтому 3V=∑hiSi=∑(ХMi, Sini)=(ХО, Sini)+(ОMi, Sini)=(ХО, ∑Sini)+3V, где О - некоторая фиксированная точка тетраэдра, следовательно, ∑Sini=0.
Далее очевидно, что свойство (20) равногранного тетраэдра является частным случаем вышеуказанной леммы, где S1=S2=S3=S4=>n1=n2=n3=n4, и так как площади граней не равны нулю, получаем верное равенство n1+n2+n3+n4=0.
В заключение рассказа о равногранном тетраэдре приведем несколько задач на эту тему.
Задача 1.
Прямая, проходящая через центр масс тетраэдра и цент