Средства эконометрического моделирования и прогноза курса акций British Petroleum
ГОУ ВПО «Российский Экономический Университет
им. Г.В. Плеханова»
Кафедра математических методов в экономике
Междисциплинарная курсовая работа
Средства эконометрического моделирования и прогноза курса акций British Petroleum
Москва, 2011 г.
В данной работе будет исследовано изменение во времени курса акций British Petroleum средствами эконометрического моделирования с целью дальнейшего прогноза.
British Petroleum – одна из крупнейших в мире нефтегазовых корпораций, относящаяся к «голубым фишкам». Компания была основана 1908 году и изначально специализировалась на добыче нефти. За более, чем вековую историю, сфера деятельности корпорации расширилась: в настоящее время British Petroleum занимается поиском месторождений и добычей нефти и газа, их транспортировкой и изготовлением из них топлива (керосин для авиации, дизельное топливо, бензин и газ). Кроме того, компания вносит вклад в развитие химической промышленности и занимается спонсорством.
Актуальность исследования заключается в большой роли финансовых рынков в современной экономике, интересе к ним больших групп людей и в занимаемом в мировой экономике месте British Petroleum.
Работа будет произведена по следующему плану, каждый пункт которого представляет собой отдельную задачу:
· Исследование исходных данных и приведение ряда к стационарному в случае нестационарности исходного ряда
· Идентификация модели
· Рассмотрение идентифицированной модели и близких к ней
· Выбор модели, наилучшим образом описывающей процесс
· Построение прогноза по выбранной модели
· Возврат к исходному ряду
Для вычислений, построения графиков и проверки гипотез использовались компьютерные программы: MS Excel и Econometric Views.
Проверка исходного ряда на стационарность
Исходные данные представлены в приложении 1 в виде таблицы. На рис. 1 показано изменение курса акций British Petroleum за период с 1 января 2010 года по 31 декабря 2010 года.
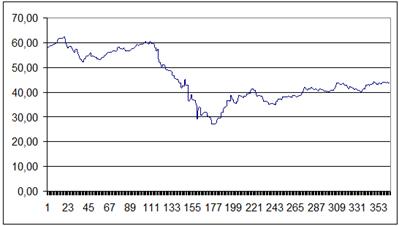
Рис. 1. Изменение курса акций British Petroleum в 2010 году
Как видно на графике, ближе к середине рассматриваемого периода произошло снижение курса акций, то есть наблюдается явно выраженный тренд. Начиная с середины рассматриваемого периода прослеживается тенденция к постепенному росту курса акций. Из-за наличия упомянутых тенденций можно сделать вывод о том, что ряд, скорее всего, не окажется стационарным, из-за чего потребуется его преобразование.
На практике для проверки гипотезы о стационарности ряда используются тесты на постоянство математического ожидания и на постоянство дисперсии. Эти тесты разделяются на параметрические и непараметрические, причём параметрические тесты можно применять только в случае нормального распределения данных.
Поэтому исследуем закон распределения исходного ряда.

Рис. 2. Гистограмма распределения исходного ряда
По полученной гистограмме, не похожей на колокол, и статистическим показателям видно (рис. 2), что данные распределены не по нормальному закону: куртозис равен 1,87, что существенно меньше трёх. Поскольку закон распределения отличен от нормального, для проверки гипотезы о стационарности ряда провести параметрические тесты нельзя, и придётся ограничиться непараметрическими тестами.
Сначала с помощью теста Дики – Фуллера проверим, не представляет ли собой исходный ряд процесс случайного блуждания.
Тест Дики-Фуллера
Таблица 1. Тест Дики – Фуллера для исходного ряда

Расчётное значение равно -1,407953. Все приведённые в таблице 1 критические значения меньше расчётного. Это значит, что нельзя отклонить гипотезу о том, что рассматриваемый процесс имеет характер случайного блуждания.
Таблица 2. Коррелограмма исходного ряда

В таблице 2 представлены значения автокорреляционной и частной корреляционной функций исходного ряда. Все значения коэффициентов автокорреляции исходного ряда выходят за пределы доверительной трубки, постепенно уменьшаясь. Первый коэффициент частной автокорреляции выходит за пределы доверительной трубки, а последующие находятся в её пределах (за исключением десятого). Подобный вид автокорреляционной и частной корреляционной функций означает, что наилучшим образом процесс описывается моделью авторегрессии первого порядка.
Если для исходного ряда построить модель АR(1), то будут получены результаты, представленные в таблице 3.
Таблица 3. Модель AR(1) для исходного ряда
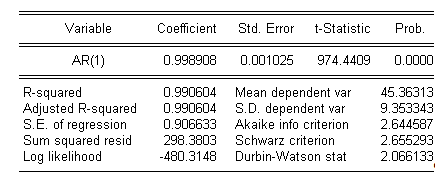
Процесс, в соответствии с данной моделью будет описываться следующим уравнением:
![]()
Коэффициент при ![]() равен 0,998908, то есть почти единице. Данное обстоятельство является свидетельством того, что процесс может носить характер случайного блуждания, что подтверждают результаты теста Дики – Фуллера.
равен 0,998908, то есть почти единице. Данное обстоятельство является свидетельством того, что процесс может носить характер случайного блуждания, что подтверждают результаты теста Дики – Фуллера.
Однако для полноты представления об исходном процессе целесообразно провести и другие тесты.
Тест Вальда–Вольфовитца (на постоянство математического ожидания)
В ходе проведения теста в ряду было выявлено девять серий, самая длинная из которых состоит из 157 элементов.
Но, согласно тесту, для того, чтобы математическое ожидание ряда было постоянным, длина самой длинной серии должна быть меньше ![]() ; и количество серий должно быть больше
; и количество серий должно быть больше
![]() .
.
Оба условия не выполняются. Тест Вальда–Вольфовитца позволяет отклонить гипотезу о постоянстве математического ожидания ряда.
Тест Манна–Уитни на постоянство математического ожидания
T1 = 150 – количество элементов в первой части ряда;
T2 = 215 – количество элементов во второй части ряда;
R1 = 43274 – сумма рангов, присвоенных элементам из первой части ряда
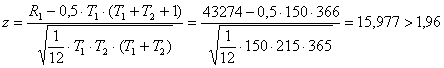
В соответствии с тестом Манна–Уитни гипотеза о постоянстве математического ожидания отклоняется.
Тест Сиджела–Тьюки на постоянство дисперсии
T1 = 150 – количество элементов в первой части ряда;
T2 = 215 – количество элементов во второй части ряда;
R1 = 23112 – сумма рангов, присвоенных элементам из первой части ряда

В соответствии с тестом Сиджела–Тьюки гипотеза о постоянстве дисперсии отклоняется.
Итак, исходный ряд не является стационарным и для дальнейшего исследования должен быть преобразован.
Конечные разностиИные рассмотренные преобразования исходного ряда и причины отказа от них представлены в приложении 2.
Лучше всего изменение курса акций описывает полином третьей степени (линейная функция ![]() , коэффициент детерминации равен 45,06%, то есть линейная функция описывает 45,06% изменчивости процесса; полином второй степени
, коэффициент детерминации равен 45,06%, то есть линейная функция описывает 45,06% изменчивости процесса; полином второй степени ![]() , коэффициент детерминации равен 68,77%, то есть полином второй степени описывает 68,77% изменчивости процесса). Коэффициент детерминации равен 72,49%, то есть полиномом третьей степени описано 72,49% изменчивости процесса во времени. На рис. 3 представлен график, демонстрирующий соответствие полинома третьей степени изменчивости процесса во времени:
, коэффициент детерминации равен 68,77%, то есть полином второй степени описывает 68,77% изменчивости процесса). Коэффициент детерминации равен 72,49%, то есть полиномом третьей степени описано 72,49% изменчивости процесса во времени. На рис. 3 представлен график, демонстрирующий соответствие полинома третьей степени изменчивости процесса во времени:
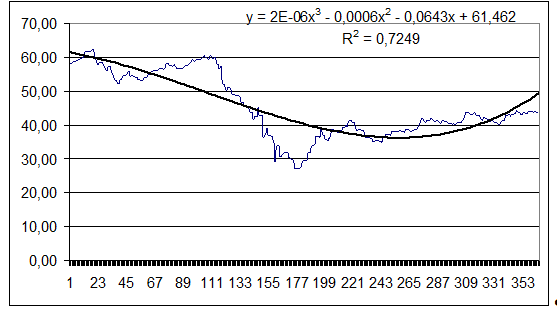
Рис. 3. Полином третьей степени в сравнении с динамикой исходного ряда
Поскольку наилучшим образом ряд описан полиномом третьей степени, в качестве преобразования исходного ряда следует избрать третьи конечные разности:
![]()
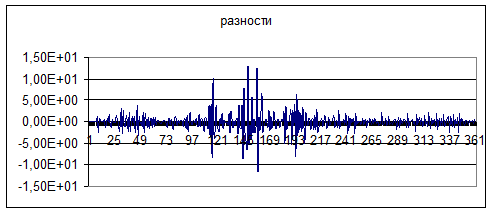
Рис. 4. График третьих конечных разностей
Как видно на графике (рис. 3), значения третьих конечных разностей колеблются около нуля. Наибольшие отклонения значений от нуля наблюдаются ближе к середине рассматриваемого периода, но в его начале и конце они малы и примерно одинаковы. Вероятно, математическое ожидание полученного ряда окажется постоянным, а о постоянстве дисперсии по графику судить сложно.
Проверим, не образовал ли ряд третьих конечных разностей процесс случайного блуждания. Для этого проведём тест Дики – Фуллера.
Тест Дики–Фуллера
Таблица 4. Тест Дики–Фуллера для ряда третьих конечных разностей

Статистика Дики–Фуллера равна -13,27932. Все приведённые в таблице критические значения больше расчётного, максимальный уровень значимости, при котором можно отклонить гипотезу случайного блуждания – 0, поэтому гипотеза о наличии у процесса характера случайного блуждания отклоняется.
Закон распределения полученного ряда
Как видно из гистограммы, имеющей более вытянутую по вертикали форму, чем характерная для нормального распределения, и статистических показателей (рис. 5), распределение полученного ряда отлично от нормального: хотя коэффициент асимметрии равен 0,6, что близко к нулю и говорит о симметричности распределения относительно среднего значения, куртозис равен 11,918, что существенно больше трёх. Поскольку закон распределения не является нормальным, для проверки гипотезы о стационарности полученного ряда параметрические тесты неприменимы, и необходимо провести непараметрические тесты.
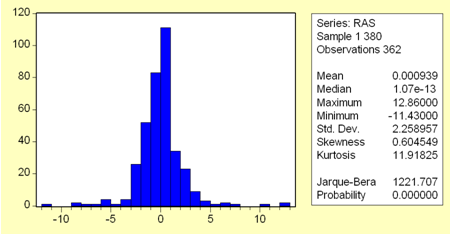
Рис. 5. Гистограмма распределения ряда третьих конечных разностей
Тест Вальда–Вольфовитца на постоянство математического ожидания
При проведении теста в ряду была обнаружена 271 серия, самая длинная из которых состоит из 4 элементов.
Согласно тесту, для того, чтобы математическое ожидание ряда было постоянным, длина самой длинной серии должна быть меньше ![]() ; и количество серий должно быть больше
; и количество серий должно быть больше
![]() .
.
Оба условия выполняются. Согласно тесту Вальда–Вольфовитца гипотеза о постоянстве математического ожидания ряда не может быть отклонена.
Тест Манна – Уитни на постоянство математического ожидания
T1 = 150 – количество элементов в первой части ряда;
T2 = 212 – количество элементов во второй части ряда;
R1 = 26982 – сумма рангов, присвоенных элементам из первой части ряда
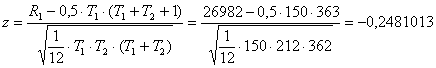 ,
, ![]()
В соответствии с тестом Манна–Уитни гипотеза о постоянстве математического ожидания не может быть отклонена.
Тест Сиджела–Тьюки на постоянство дисперсии
T1 = 150 – количество элементов в первой части ряда;
T2 = 212 – количество элементов во второй части ряда;
R1 = 26479 – сумма рангов, присвоенных элементам из первой части ряда
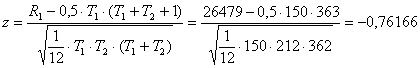 ,
, ![]()
Согласно тесту Сиджела–Тьюки гипотеза о постоянстве дисперсии не может быть отклонена.
Итак, полученный ряд можно рассматривать как стационарный.
Эконометрические модели для конечных разностей
Идентификация модели
Изучив вид автокорреляционной и частной автокорреляционной функций ряда (таблица 5), полученного с помощью конечных разностей, можно предположить, какая модель наилучшим образом будет описывать процесс.
Таблица 5. Коррелограмма ряда третьих конечных разностей

Первые два коэффициента автокорреляции ряда выходят за пределы доверительной трубки. Коэффициенты частной корреляции, вплоть до одиннадцатого включительно также выходят за пределы доверительной трубки, а их значения уменьшаются вплоть до шестого включительно.
Таблица 6. Критические значения для Q-Stat при уровне значимости 0,05
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Критическое значение | 3,84146 | 5,99146 | 7,81473 | 9,48773 | 11,0705 | 12,5916 |
| t | 7 | 8 | 9 | 10 | 11 | 12 |
| Критическое значение | 14,0671 | 15,5073 | 16,919 | 18,307 | 19,6751 | 21,0261 |
Подобные работы: