Генетико-статистический анализ комбинационной способности сортов и форм яровой мягкой пшеницы по коэффициенту хозяйственной эффективности фотосинтеза
Актуальность темы. Пшеница является одной из важнейших продовольственных культур. Она играет важную роль в производстве зерна и мирового рынка. К качеству пшеницы ставят перед селекционерами следующие задачи: высокая продуктивность сортов, высокая урожайность, качества зерна, устойчивости к неблагоприятным факторам среды, устойчивость к засухе, полеганию, болезням и вредителям.
Однако в настоящее время генетическая основа формирования количественных признаков в гибридных популяциях от скрещивания озимой и яровой пшеницы изучена далеко не достаточно. Дальнейшее повышение эффективности селекции с привлечением лучших сортов во многом зависит от изучения генетики важнейших количественных признаков, определяющих продуктивность растений. Эти признаки имеют полигенную природу и степень их проявления находится в значительной зависимости от условий произрастания.
Цель работы - определить комбинационную способность сортов и форм яровой мягкой пшеницы по коэффициенту хозяйственной
эффективности фотосинтеза в системе топкроссных скрещиваний. В связи с данной целью решаются следующие задачи:
- проведение дисперсионного анализа исходных данных по коэффициенту хозяйственной эффективности фотосинтеза у гибридов Р};
- установление вклада аддитивных и неаддитивных эффектов генов в наследование изучаемого признака на основе дисперсионного анализа комбинационной способности;
- выявление эффективных доноров по коэффициенту хозяйственной эффективности фотосинтеза по результатам расчёта эффектов ОКС;
- выявление комбинаций гибридов с высоким эффектом гетерозиса на основе определения варианс СКС;
- разработка оптимальной стратегии селекции по коэффициенту хозяйственной эффективности фотосинтеза по результатам анализа комбинационной способности.
В работе описаны математические методы оптимизации селекционного процесса. Определена комбинационная способность сортов и форм яровой мягкой пшеницы по коэффициенту хозяйственной эффективности фотосинтеза и предложена стратегия селекции по данному признаку.
Объектом исследований служит яровая мягкая пшеница, главная культура Западной Сибири. Предмет исследования - изучение комбинационной способности родительских сортов и форм по признаку - коэффициенту хозяйствен - ной эффективности фотосинтеза. Для определения комбинационной способности применимы теоретические, эмпирические и экспериментальные методы исследования.
1. Применение генетико-статистических методов на разных этапах селекционного процесса
1.1 Количественные и качественные признаки
Различают два основных типа изменчивости: количественную, поддающуюся измерению, и качественную, измерение которой затруднено или невозможно.
Количественные признаки могут иметь непрерывную (высота растений) или дискретную (коэффициент хозяйственной эффективности фотосинтеза) изменчивость. Качественные описываются в шкале наименований (цвет лепестков, пол) или в порядковой, балльной шкале (степень поражения растений бурой ржавчиной).
Деление на количественные и качественные признаки условно. Например, качественный признак, цвет лепестков, можно выразить количественно - дли - ной волны отраженного света. Количественный признак, высота растения, можно представить как качественный признак с тремя градациями (низкое, среднее, высокое). Наследственная изменчивость признака в популяции определяется полиморфными локусами, генами с различными аллельными состояниями. При малом числе таких генов (1 - 2) и сравнительно слабом модификационном влиянии среды на признак особи можно отнести к небольшому числу различающих классов. Такую изменчивость можно считать качественной, так как аппроксимирующие кривые (пунктир) практически не пересекаются. Применимы методы анализа классической менделеевской генетики (1).
При усилении модифицирующих влияний условий выращивания на проявление генотипа величина признака, может иметь сглаженное трехвер - шинное распределение. Трудно выявить «многовершинность», то можно отнести к типично количественному с непрерывной изменчивостью обусловленной большим числом генов с разной силой влияния на степень выражения признака и с различными внутри - и межлокусными взаимодействиями.
Даже при незначительных средовых модификациях гистограммы для отдельных генотипов в значительной степени накладываются. Это типичная ситуация детерминации хозяйственно ценных количественных признаков. Таким образом, возникает задача выбрать приемлемую модель, которая описывает изменчивость признака в генетических исследованиях. Используют три класса моделей (1):
1. Олигогенное наследование применяют, если среди множества генов можно выделить 1 - 3 олигогена, с преимущественным влиянием на изменчивость признака в популяции. Модель основана на популяционно - генетическом анализе и, является усложненной модификацией менделевской генетики. У растений генетическая структура признака неизвестна и подвержена сильным средовым модификациям. Поэтому применение в практике селекции ограничено.
2. Полигенное наследование, предложено Кеннетом Мазером. Он предложил, что количественный признак детерминируется большим количеством числом генов со слабым действием (полигены). Эти гены в той или иной степени сцеплены в группы (блоки), которые в результате кроссинговера могут разделяться, проявляться как новые гены, переформироваться в другие группы. К данному классу биометрико - генетических моделей изменчивости признака относится, например метод Хеймана.
3. Фенотипические модели количественных признаков. Этот класс моделей получил широкое распространение в селекционно - генетических исследованиях. В этих моделях математически представлены укрупненные влияния на признак генотипических, средовых эффектов и их взаимодействия. Феноменологические модели первоначально разработаны Рональдом Фишером для целей селекции. Эти модели позволяют обобщать ограниченные объемы опытных данных, полученных из разных условий выращивания, прогнозировать фенотипические значения или уровень изменчивости изучаемого признака, а также оценивать отбор лучших генотипов. Феноменологические модели учитывают влияние генетических механизмов и не позволяют проводить детальный анализ генетической структуры признаков (1).
1.2 Генетика коэффициента хозяйственной эффективности фотосинтеза
генетический пшеница селекционный фотосинтез
Более высокий выход зерна от общей надземной массы растений - одно из основных требований, предъявляемых к сортам интенсивного типа. Для селекции на засухоустойчивость особую ценность представляют формы с умеренным развитием вегетативной массы, с высокой интенсивностью процессов реулитизации веществ в зерно и аттрагирующей способностью колоса. При достаточном увлажнении гибридов пшеницы повышенное значение коэффициента хозяйственной эффективности фотосинтеза имели более низкорослые гибриды = -0,806 ±0,90). В условиях раннелетней и комплексной засухи связь
между этими признаками отсутствовала. Где преобладает раннелетняя засуха, возможно дальнейшее увеличение коэффициента хозяйственной эффективное - ти фотосинтеза.
Наиболее высокими показателями наследуемости характеризуется коэффициент хозяйственной эффективности фотосинтеза (Я2 = 24,9 - 61,9%). Коэффициент хозяйственной эффективности фотосинтеза в меньшей степени подвержены влиянию модификаций (6).
1.2.1 Эколого-генетические модели количественных признаков
Анализ большого объема наследования показывает, что генетические могут меняться: при изменении набора генотипов, средовых условий (местность, год, условия агротехники и т.д.), конкурентных отношений в агроценозе в зависимости от густоты посева, в процессе реализации генетической информации в онтогенезе. Причина изменении дифференциальной активности генов, влияющих на изменчивость количественных признаков. В. А. Драгавцев связывает явление с понятием переопределения генетических формул признака, что любой признак продуктивности не всегда имеет стабильную систему генов.
Таким образом, ценность традиционного генетического анализа относительна, генетические параметры могут, отнесены только к конкретной эколого-генетической ситуации. Необходимо дальнейшее совершенствование биометрических методов в генетике, разработка новых эколого-генетических моделей количественных признаков, которые могли бы преодолеть указанные недостатки существующих моделей.
В. А. Драгавцев и др. (1), анализируя различные биометрико-генетические модели для описания наследования количественных признаков, пришел к выводу, что большинство моделей несовершенны. По мнению В. А. Драгавцева, модель статична, она отражает конкретную постоянную эколого-генетическую ситуацию. Он предложил новую модель эколого-генетического контроля количественных признаков, которая основана на лабильной генетической формуле количественного признака: последняя может «переопределяться» при смене лимитирующего фактора среды. Эта модель позволяет прогнозировать генотипические корреляции, адаптивные свойства генотипов, объясняет причину взаимодействия генотип - среда и т.д.
Предлагаемая модель признака носит качественный характер, ориентируется на конкретную культуру, популяцию и требует знания смены лимитирующих факторов в онтогенезе в конкретных условиях произрастания. Следует отметить, что «переопределение» генетических формул признака в результате «включения» или полного «выключения» определенных генов в различных условиях среды не является единственной причиной взаимодействия генотип - среда и изменения корреляций (1).
А. А. Жученко и В. С. Нестеров предложили регрессионную эколого-генетическую модель детерминации количественного признака сорта (1):
![]() ……., (1)
……., (1)
где у - фенотипическое значение количественного признака; g0 - характеризующий реакцию на общий (постоянный) фон выращивания; gi, gij- модификационная изменчивость сорта по реакции на факторы среды и взаимодействие факторов ![]() , ....(основные факторы среды, влияющие на значение количе - ственного признака).
, ....(основные факторы среды, влияющие на значение количе - ственного признака).
Эти параметры могут служить мерами адаптивности генотипа к конкретному лимитирующему фактору (сочетанию факторов) среды. Модель может быть использована для решения селекционных и агротехнических задач. Однако ее построение и применение требует накопления и использования обширной базы эколого-генетической информации и реализации сложных алгоритмов расчета. Многолетние попытки построения регрессий урожайности сортов на непосредственно измеренные факторы среды, как правило, не приводят к адекватным моделям (1).
1.3 Математико-статистические методы подбора пар для скрещивания
При скрещивании географически отдаленных форм в потомстве ожидается повышенная генетическая изменчивость и, легче обнаружить трансгрессивные рекомбинанты. Географическую отдаленность можно связать с генетической дивергентностью родителей, т.е. с расхождением линий или популяций, происходящих от общего предка, в результате отбора или изоляции. В процессе эволюции в условиях географической отдаленности в местных популяциях закрепляются и накапливаются гены с наибольшей адаптивной ценностью к специфическим условиям среды. У отдельных родителей хозяйственные признаки контролируются различными наборами аллелей, случайные рекомбинации которых вызывают трансгрессивное расщепление.
Поэтому целесообразнее используют термин генетической отдаленности илидивергентности - несходства аллельного состава родительских форм. Основная проблема при оценке степени дивергентности по генам, определяющим различия форм по хозяйственно ценным признакам, - недостаток сведений о наследовании этих признаков, т.е. о связи фенотипических выражений признаков с генотипом. Поэтому часто пытаются оценить общее несходство аллельного состава родительских форм в надежде, что при этом будет учтено различие и по генам хозяйственно - ценных признаков (1).
Генетическую дивергенцию можно выразить через специальные пара - метры с помощью методов многомерного статистического анализа комплекса количественных признаков.
Естественной мерой отдаленности потенциальных родителей служит евклидово расстояние. Евклидово расстояние между двумя генотипами определяется по теореме Пифагора (2):
![]() (2)
(2)
Где xlk , x2k - среднее значение k-го признака у 1-го и 2-го сортов.
Для оценки общей генетической дивергентности по всему геному в показатель следует включать максимальное число количественных признаков. Если у признаков различные размерности, то евклидово расстояние может оказаться неверным. Данный метод позволяет выявить группы генетически тесно связанных признаков и отобрать от каких групп по одному признаку для использования в евклидовом расстоянии (1).
1.3.1 Близость к идеальным значениям по комплексу признаков
Для прогноза близости потомства от скрещивания выбранных родителей к заданному идеалу Дж. Графиус разработал векторный метод. Под идеалом понимается модель сорта - воображаемый сорт, имеющий заданные величины признаков, оптимальные для конкретных условий среды.
Д. Педерсон упростил этот метод и предложил подобрать родительские формы, дополнительно задавая селекционным признакам различные веса – допустимые отклонения от идеальных значений. Суть метода Педерсона заключается в следующем. У каждого из т потенциальных родительских сортов учтено N количественных признаков. Номер признака обозначен у. Каждому признаку селекционер - эксперт задает идеальное значение Ij,а также отклонение от идеала Dj. Цель скрещивания - получение гибридной популяции со средним значением каждого признака в интервале Ij ± Dj (1).
Основная проблема прогнозирования - сложная генетическая связь величин признаков родителей и популяционных средних в потомстве их скрещиваний. Поэтому в методе Педерсона предлагается, что среднее значение каждого признака в позднем поколении скрещивания равно средневзвешенным значениям этого признака у родителей. Таким образом, популяционная средняя по j-му признаку (![]() j) потомства равна (3):
j) потомства равна (3):
![]() (3)
(3)
где хij – значение j-го признака у i-го родителя; Пi- доля i-го родителя в геноме популяции потомства. Обычно селекционер располагает большим набором сортов и форм, изучаемых по хозяйственным признакам в конкурсном и предварительном сортоиспытании, производстве или в коллекционном питомнике. Модификация метода оценки близости к идеалу, предложенную С. П. Мартыновым (4). Мерой отклонения ожидаемого потомства от модели идеального сорта в модификации является уравнение:
![]() (4)
(4)
где Ij ,![]() j значение j -го признака у идеала и ожидаемого потомства; аj -весовoй коэффициентj-го признака;
j значение j -го признака у идеала и ожидаемого потомства; аj -весовoй коэффициентj-го признака; ![]() - стандартное отклонениеj-го признака в наборе сортов.
- стандартное отклонениеj-го признака в наборе сортов.
В этом случае вектор идеала представляет собой совокупность оптимальных (наилучших) значений селекционных признаков, полученных при испытании сортов в различных условиях.
В методе С. П. Мартынова признаки могут быть разработаны на несколько групп с одинаковыми весами для признаков в одной группе. Их подсчитывают по формуле (5):
а = ркN / пк;к = 1,....,G,(5)
где рк - заданный вклад k -й группы признаков в некоторую меру сходства ожидаемого потомства и заданного идеала; N - общее число признаков; пк - число признаков в k-й группе; G - число групп.
Общим недостатком методов, оценивающих близость к идеальному сорту средних значений признаков ожидаемого потомства, является отсутствие учета генетического разнообразия популяции потомства. Один вариант скрещивания может давать большую близость средних к идеалу, но иметь низкое генетическое разнообразие популяции потомства по изучаемым признакам, а второй - дальше от идеала по средним, но с гораздо большей генотипической изменчивостью. Во второй популяции потомства больше вероятность отобрать формы, близкие к идеальному сорту. Поэтому генетическое разнообразие потомства также оценивать и учитывать при подборе родительских форм (1).
1.3.2 Комбинационная способность и методы ее определения
Общую комбинационную способность (ОКС), как правило, устанавливают на основе топкроссных испытаний. Для определения специфической комбинационной способности (СКС) необходимы диаллельные скрещивания, которые включают в себя все возможные комбинации скрещивания между серией сортов и линий. Соответствующие методы определения комбинационной способности разработал Б. Гриффинг, предложивший четыре метода анализа диаллельного скрещивания:
1. Изучают родительские формы, F1 - гибриды прямых и обратных скрещиваний всего m2 генотипов.
2. Изучают родительские формы и F1 полученные в результате прямых скрещиваний, - всего m(m+1)/2 генотипов.
3. Изучают только прямые и обратные гибриды F1 - всего m(m-1) генотипов.
4. Изучают только прямые гибриды F1 - всего m(m-1)/2 генотипов.
Для анализа комбинационной способности в целях гетерозисной селекции, как правило, применяют метод IV.
Топкроссы применяют для определения общей и специфической комбинационной способности при селекции на гетерозис. Для этого линии и сорта скрещивают с одним или несколькими сортами - анализаторами (тестерами). При этом в селекции самоопыляющихся растений большое значение имеет определение эффектов общей комбинационной способности, по величине которых можно судить о донорских свойствах скрещиваемых форм (1).
Поликросс требует определенной подготовительной работы и планирования. Однако при использовании поликросса не требуется проводить оценку комбинационной способности родителей. Применяется главным образом к тем перекрестноскрещивающимся культурам, у которых получение семян от контралируемых скрещиваний затруднено. Результаты поликроссного испытания указывают на сорта, имеющие повышенную комбинационную способность, которые затем рекомендуют в состав синтетической популяции. По методам Гриффинга возможны два варианта оценки исходного материала. Вариант I (модель I) применяют, когда родительские формы для исследования отбирают специально и необходимо оценить их комбинационную способность. Формы одновременно являются тестерами, с помощью которых выявляют комбинации скрещиваний. Вариант II (модель II) используют, когда родительские формы отобраны случайно из популяции, которые необходимо оценить (тестером служит исследуемая родительская популяция). Исходные линии случайно отобраны из популяции, полученной длительным самоопылением (без отбора) генотипов исследуемой популяции. В данном случае представляют интерес не сами пара - метры отдельных родительских линий, а компоненты генотипической и дисперсии признака в исходной популяции. Значение признака для гибридной комбинации между i-м j -м родительским сортом в k-м повторении можно выразить в биометрической модели следующий вид уравнения (6):
xijk=µ+gi+gj+sij+ri+ek(6)
где хijk- величина признака у гибрида F1 между i-й и j-й родительскими линиями в k-м повторении; µ- среднее значение признака в наборе линий и гибридов F1, gi, gj эффект общей комбинационной способности i-й и j-и родительских линии; sij - эффект специфической комбинационной способноcти; ri - реципрокный эффект при скрещивании i-й и j-й линий; ек- эффект, обусловленный случайной ошибкой в k-м повторении.
Существенность отношения определяемая по Р - критерию Фишера, указывает, что между исследуемыми гибридами (или гибридами и линиями) имеются различия по величине признака, случайные ошибки опыта. Если различия не значимы, дальнейший анализ комбинационной способности не проводят. Оценки и их разности, необходимые для дальнейшего анализа, несут случайные ошибки, которые характеризуются дисперсиями ошибок (var) (7):
![]() (7)
(7)
Третий метод Гриффинга. Оценка одного из вкладов в дисперсию СКС меньше нуля. Это объясняется неучтенными ошибками опытов и, возможно, неполным соответствием данных стандартным предположениям дисперсионного анализа (1).
Теоретическая основа метода Хеймана. Данный метод базируется на предположении, что количественный признак детерминирован k полиморфными локусами, точнее блоками сцепленных полигенов. Каждый локус в анализируемом наборе из родительских линий может иметь два аллельных состояния. Вклад этих генных различий в оценки статистических параметров, сред - них, дисперсий, ковариаций будут следующими (без учёта ошибок опытов). Дисперсия величин признака у родительских линий (8):
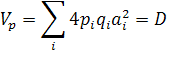
где ∑ - сумма по всем k полиморфным локусам; D - изменчивость аддитивных эффектов аiу родителей с учетом частот pi и qi
Метод Хеймана можно рассмотреть и как генетический анализ популяции. Из уравнении следует, что при выполнении требований на Э влияют только аддитивные, а на Н1 и Н2 - доминантные эффекты. Отношение характеризует степень доминирования в экспериментальном материале, среднюю по всем полиморфным локусам.
Отношения позволяют сделать выводы относительно генетической детерминации количественного признака у изученных родительских форм. В этом состоит так называемый параметрический вариант метода Хеймана. Используется также регрессионный анализ Хеймана. Метод Хеймана обладает определенной робастностью - устойчивостью к неполному удовлетворению шести требований. Вопрос о проверке выполнения требований и о пределах устойчивости выводов до настоящего времени решен не полностью. Сравнительно низкие требования к объёму и структуре эксперимента позволяют методу Хеймана оставаться популярным в селекционно-генетических исследованиях растений (1).
1.4 Методы отбора
В селекции растений используют два основных метода отбора - массовый и индивидуальный.
Массовый отбор по фенотипу и совместный посев отобранных растений применяют для перекрестно- и самоопыляющихся культур. Отбору растений или колосьев предшествует выращивание массовых популяции, а иногда и более поздних поколений для повышения степени гомозиготности у самоопылителей.
Индивидуальный отбор применяют в ранних поколениях. Семена отобранных растений высевают отдельными рядками. Затем отбирают лучшие семьи и линии с последующим размножением перспективных номеров.
Индивидуальный отбор применяют как для самоопылителей, так и для перекрестников (в том числе у двулетних и многолетних растений, у двудомных видов) (3).
Отбор более эффективен по качественным признакам, по которым четко идентифицируются генотипы. По продуктивности ц другим количественным признакам отбор (особенно в ранних расщепляющихся поколениях) не всегда оказывается эффективным. Это может быть результатом маскирующих эффектов следующих генетических и средовых факторов:
- продуктивность растения в большой степени обусловлена внешней средой (пестротой почвенного плодородия), а также конкуренцией между растениями в посеве;
- в ранних поколениях фенотипический отбор самоопыляющихся растений по продуктивности слабо связан с урожайностью в продвинутых поколениях;
- взаимодействие генотип - среда.
Конечная цель селекции самоопылителей - получение гомозигот для использования в качестве линейных сортов. При этом не каждый генотип, характеризующийся высокой продуктивностью в чистом посеве, будет в достаточной мере конкурентоспособным в смеси с другими генотипами. В экспериментах установлено, что нередко существует антагонизм между урожайностью и конкурентоспособностью. Поэтому естественный отбор благоприятствует агрессивным генотипам, обладающим низкой продуктивностью (1).
1.4.1 Оценка наследуемости Н2 и h2, методы, его определения, формы и понятия
Отбор будет действительным только в том случае, если хотя бы часть наблюдаемой фенотипической изменчивости признака, подлежащего отбору, обусловлена генотипически. Чем больше доля генотипически обусловленного варьирования признака в его общей фенотипической изменчивости, тем теснее связь между генотипом и фенотипом и тем эффективнее отбор. Мерой доли генотипически обусловленной изменчивости в общем фенотипическом варьировании служит коэффициент наследуемости. Косвенно по коэффициенту наследуемости можно сулить и о доле изменчивости, обусловленной влиянием внешней среды. Коэффициентом наследуемости в широком смысле называется отношение генотипической вариансы к общей вариансе (9):
![]() (9)
(9)
где Vg - генотипическая варианса; Vрh - общая фенотипическая варианса.
Коэффициент наследуемости в узком смысле показывает отношение вариансы, которая вызвана прямым аддитивным действием генов, к общей фенотипической вариансе (10):
где Va - вызвана прямым аддитивным действием генов; Vрh– общая фенотипическая варианса.
Однако сложно определять коэффициент. Коэффициент может варьировать от 0 до 1 (3).
1.4.2 Коррелятивный сдвиг СК
Корреляция признаков приводит к тому, что при отборе по одному из них потомство отобранных особей отличается от исходной популяции не только по признаку, но и по всем другим признакам, которые коррелируют с отбираемым признаком. Это косвенное действие отбора называется коррелятивным сдвигом (СR). Если отбор ведут по некоторому признаку x, который коррелирует с другим признаком у, то коррелятивный сдвиг составляет (11):
СRу=ihxhyraσphy,(11)
где i - интенсивность отбора.
Коррелятивный сдвиг служит причиной неожиданных эффектов отбора и может быть использован целенаправленно при его проведении. Возможны три случая.
1. Улучшаемый признак имеет низкую наследуемость, но он коррелирует с другими признаками, имеющими более высокую наследуемость. В данном случае проводят косвенный отбор по признакам с более высокой наследуемостью, если выполнено условие: hуrа>hх.
2. Признак, подлежащий генетическому улучшению, сложно определить, но он хорошо коррелирует с признаками, которые легче оценить.
3. Признак, по которому осуществляют отбор, можно оценить только на последних этапах индивидуального развития. Но он коррелирует с признаками, различимыми уже на первых этапах. В этом случае корреляция признаков используется для раннего отбора (2).
1.4.3 Селекционный дифференциал 8, интенсивность отбора 1
Интенсивность отбора можно определить с помощью селекционного дифференциала (S) или интенсивности отбора (i). Относительную силу воздействия внешней среды и генетического влияния на признак измеряют с помощью коэффициента наследуемости (h2). 'Самой простой мерой интенсивности отбора по количественным признакам служит селекционный дифференциал, обозначаемый 8. Он представляет собой разность между средней величиной признака в популяции отобранных особей (![]() ) и соответствующей средней его величиной в исходной популяции (
) и соответствующей средней его величиной в исходной популяции (![]() ) (12):
) (12):
![]() (12)
(12)
Пример. Если в популяции со средней высотой растений (![]() ) = 125 см отбирают все низкорослые растения со средней высотой (
) = 125 см отбирают все низкорослые растения со средней высотой (![]() ) = 90 см, то полученный селекционный дифференциал составляет 35 см.
) = 90 см, то полученный селекционный дифференциал составляет 35 см.
Чем интенсивнее ведется отбор, тем выше значение 8. С помощью 8 строгость отбора по определенному признаку в различных популяциях можно сравнить только в том случае, если изучаемые популяции имеют одинаковую изменчивость определенного признака. Чтобы получить от величины изменчивости меру интенсивности отбора, надо выразить селекционный дифференциал в единицах среднего квадратного отклонения данного признака
(σp) (13):
![]() (13)
(13)
Показатель i и обозначает интенсивность отбора (3).
1.4.4 Коэффициент на отбор, К, респонс
Коэффициент наследуемости даёт возможность предсказать результат (сдвиг) отбора. Сдвигом отбора, илиреспонсом R, называется наследуемая часть селекционного дифференциала S. Она равна произведению селекционного дифференциала на коэффициент наследуемости (14):
![]() (14)
(14)
При выражении селекционного дифференциала через интенсивность отбора (S = i![]() σp)формула приобретает вид (15):
σp)формула приобретает вид (15):
![]() (15)
(15)
С помощью формулы сдвига при отборе можно делать различные прогнозы, в частности предсказать, какой сдвиг R может быть достигнут при определённом селекционном дифференциале S или какое значение S необходимо, чтобы при определённом коэффициенте наследуемости обеспечить заданный сдвиг R (6).
1.4.5 Оценка индекса отбора I
Этот индекс позволяет на основе математической оптимизации получить наиболее выгодные сочетания признаков у будущего сорта. Индекс отбора имеет вид (16):
![]() (16)
(16)
гдеx1, х, хп - фенотипические значения признаков, на которые ведётся отбор;
b1,b2,bn - коэффициенты признаков.
Для вычисления индекса отбора требуется определить фенотипические и генотипические (аддитивные) вариансы по каждому признаку и ковариансы по каждой паре признаков. Кроме того, устанавливают факторы экономического значения признаков (желательный сдвиг). Затем, решая систему нормальных уравнений, находят коэффициенты признаков.
Например, если проводят одновременный отбор по двум признакам - урожай зелёной массы и число початков кукурузы или урожай хлопка-сырца и длина волокна хлопчатника, то для нахождения коэффициентов признаков (b1,b2) используют систему из двух нормальных уравнений (17,18):
![]() (уравнение I)(17)
(уравнение I)(17)
![]() (уравнение II)(18)
(уравнение II)(18)
где ![]() - фенотипическая варианса первого признака;
- фенотипическая варианса первого признака; ![]() - аддитивная варианса первого признака;
- аддитивная варианса первого признака;![]() - фенотипическая коварианса первого и второго признаков;
- фенотипическая коварианса первого и второго признаков;![]() - аддитивная коварианса; а1 и а2 - факторы экономического значения первого и второго признаков соответственно; b1 иb2 - искомые коэффициенты первого и второго признаков соответственно (6).
- аддитивная коварианса; а1 и а2 - факторы экономического значения первого и второго признаков соответственно; b1 иb2 - искомые коэффициенты первого и второго признаков соответственно (6).
1.5 Оценка устойчивости к полеганию
В полевых условиях устойчивость селекционных материалов к полеганию оценивают по пятибалльной шкале: 5 - полегание отсутствует, 4 - слабое полегание, стебли слегка наклонены, 3 - среднее полегание, наклон стеблей к поверхности почвы под углом 45°, 2 - сильное полегание, 1 - очень сильное полегание, механизированная уборка невозможна.
Устойчивость растений к полеганию в полевых условиях можно определять по силе, приложенной для выдёргивания растений из почвы, с помощью динамометра.
Для повышения объективности глазомерной балльной оценки устойчивости к полеганию растений в полевых условиях В.С. Кузнецов предложил учитывать балл устойчивости к полеганию по следующей формуле (19):
![]() (19)
(19)
где Б - балл устойчивости к полеганию;
в - высота растений, см;
С - слой полёгших стеблей, см.
И. Рагастис предложил формулу, близкую к вышеприведённой (20):
![]() (20)
(20)
где М- показатель устойчивости к полеганию, %;
х - высота полёгшего стеблестоя, см;
Н - высота растения, см.
Например, 40 см - высота стеблестоя, а у растения высотой 100 см показатель устойчивости равен 40%. Чем выше данный показатель, тем выше устойчивость (7).
1.5.1 Оценка засухоустойчивости
Засушник представляет собой деревянный или металлический каркас, покрываемый подвижной крышей из полиэтиленовой плёнки. При выпадении дождя крышу надвигают. Ширина засушника - не более шести метров, длина - произвольная. Вокруг роют канавку шириной 30-35- см и глубиной 60-70 см для изоляции от воды. Корни растений изолируют от грунтовых вод. Для этого на глубине два метра укладывают два слоя полиэтиленовой пленки. Бывают также стационарные стеклянные засушники (оранжереи) и засушники со съёмной крышей из брезента или клеёнки. В засушливую погоду в засушнике моделируют атмосферную и почвенную засухи, во влажные годы - только почвенную
При оценке засухоустойчивости с использованием засушника для удобства сравнения изучаемых сортов предложена балльная система оценки (табл. 1).
Таблица 1 - Балльная система оценки засухоустойчивости
| Засухоустойчивость | ||
| % | Балл | По классификатору ВИР |
| 90,1-100,0 | 5 | 9 |
| 80,1-90,0 | 4 | 7 |
| 70,1-80,0 | 3 | 5 |
| 60,1-70,0 | 2 | 3 |
| 50,1-60,0 | 1 | 1 |
Суть данной системы оценки состоит в том, что при оценке селекционного материала учитывают два показателя - физиологическую засухоустойчивость (в % к контролю) и абсолютную зерновую продуктивность в условиях засухи (засушник). Чтобы одновременно анализировать оба показателя, можно использовать систему координат. По оси абсцисс откладывается величина физиологической засухоустойчивости сортов, а по оси ординат - его урожайность в условиях засухи. Наибольший интерес для селекции на засухоустойчивость представляют сорта, которые по обоим показателям имеют самые высокие значения (6).
1.5.2 Оценка устойчивости к болезн