Граничные условия на стыке двух диэлектриков. Теорема о циркуляции

М.И. Векслер, Г.Г. Зегря

Любая граница раздела двух сред может считаться плоской на достаточно малом участке. Кроме того, в пределах достаточно малого участка поле векторов \vec{D}, \vec{E}, \vec{P}можно считать однородным на каждой из сторон. Составляющие указанных векторов Dn, En, Pn, перпендикулярные к границе, называются нормальными, а \vec{D}_{\tau}, \vec{E}_{\tau}, \vec{P}_{\tau}, параллельные границе, - тангенциальными компонентами.

На незаряженной границе двух диэлектриков нормальные и тангенциальные компоненты преобразуются следующим образом:

D_{n1}=D_{n2}, \vec{E}_{\tau 1} = \vec{E}_{\tau 2}

(36)

Левое соотношение получается из теоремы Гаусса, примененной к области в форме очень тонкого параллелепипеда, серединной плоскостью которого является граница раздела диэлектриков. Для получения второго соотношения привлекается теорема о циркуляции

\int\limits_L\vec{E}\cdot{\rm d}\vec{l} = \int\limits_S rot\vec{E}\cdot{\rm d}\vec{S}

(37)

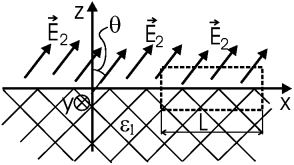
Контуром служит узкая прямоугольная рамка, плоскость которой перпендикулярна к границе раздела, рассекающей рамку пополам. Левая часть равенства есть (\vec{E}_{\tau 1}-\vec{E}_{\tau 2}) \cdot\vec{l}, а правая равна нулю из электростатического уравнения Максвелла (rot\vec{E}=\vec{0}). Эаметим, что теорема о циркуляции - это математический закон, применимый к любому векторному полю, как и теорема Гаусса.

Подобные работы:

Актуально: