Основи теорії сигналів
Основи теорії сигналів
Спектральний метод аналізу, заснований на поданні сигналу у вигляді суми (або інтегралу) гармонічних складових (гармонік) і подальшому розрахунку проходження кожної з гармонік через коло. Вихідний сигнал знаходиться на основі принципу накладання у вигляді суми відгуків на кожну з гармонік вхідного сигналу. Сукупність гармонік, на які розкладаються сигнали, називається їх спектрами.
Вивчення спектрів розпочинається з періодичних імпульсних відеосигналів.
Імпульсними називаються струми і напруги кінцевої енергії, миттєві значення яких відмінні від нуля впродовж деякого (як правило, досить невеликого) інтервалу часу.
Періодичні послідовності імпульсів (рис. 1) відносяться до періодичних несинусоїдних процесів і знаходять широке використання в радіоелектроніці.
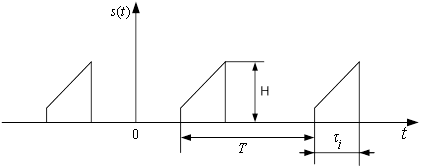
Рисунок 1 – Періодична послідовність імпульсів
Періодичні послідовності імпульсів характеризуються їх формою, тривалістю ![]() ,
, ![]() періодом повторення
періодом повторення ![]() (або частотою
(або частотою ![]()
![]() ), висотою (максимальним значенням) –
), висотою (максимальним значенням) –![]() .
.
Тривалість імпульсів ![]() знаходять на деякому рівні від висоти
знаходять на деякому рівні від висоти ![]() (у границі на нульовому рівні), або як інтервал часу, в якому міститься визначена потужність імпульсу (зазвичай 90
(у границі на нульовому рівні), або як інтервал часу, в якому міститься визначена потужність імпульсу (зазвичай 90![]() або більше).
або більше).
Інколи вводиться також вторинний параметр – щілинність:
![]()
![]() .
.
Періодична послідовність імпульсів, описується функцією![]() , яка задовольняє умови Діріхле і може бути подана нескінченим рядом (рядом Фур’є) гармонік з частотами, кратними частотам слідування
, яка задовольняє умови Діріхле і може бути подана нескінченим рядом (рядом Фур’є) гармонік з частотами, кратними частотам слідування ![]() ,
, ![]() :
:
![]() , (1)
, (1)
де 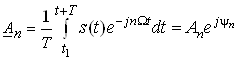 – комплексна амплітуда
– комплексна амплітуда ![]() -ї гармоніки,
-ї гармоніки,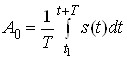 – постійна складова імпульсів (середнє значення).
– постійна складова імпульсів (середнє значення).
Сукупність амплітуд гармонік ![]() називають спектром амплітуд або амплітудно-частотним спектром (АЧС).
називають спектром амплітуд або амплітудно-частотним спектром (АЧС).
Сукупність початкових фаз ![]() називають спектром фаз або фазочастотним спектром (ФЧС).
називають спектром фаз або фазочастотним спектром (ФЧС).
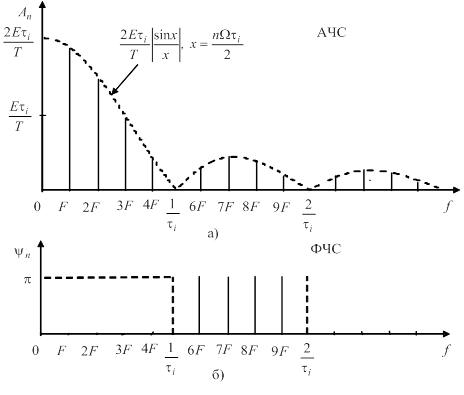
АЧС і ФЧС зображують у вигляді графіків, в яких за віссю абсцис відкладають частоту (![]() або
або ![]() ), а за віссю ординат – амплітуди гармонік у АЧС і початкові фази у ФЧС (рис. 2). Властивістю спектра періодичного коливання є поступове зменшення амплітуд гармонік зі зростанням їх частоти. Це дозволяє оперувати з нескінченними межами сум у (1), а з сумами обмеженими
), а за віссю ординат – амплітуди гармонік у АЧС і початкові фази у ФЧС (рис. 2). Властивістю спектра періодичного коливання є поступове зменшення амплітуд гармонік зі зростанням їх частоти. Це дозволяє оперувати з нескінченними межами сум у (1), а з сумами обмеженими ![]() . Кожній парі ординат графіків АЧС і ФЧС відповідна частота однієї з гармонік, тобто
. Кожній парі ординат графіків АЧС і ФЧС відповідна частота однієї з гармонік, тобто ![]() ,
,![]() ,
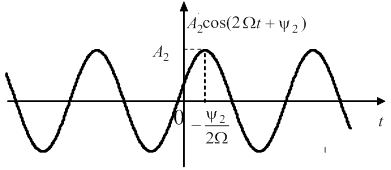
,![]() повністю визначають параметри цієї гармоніки. Наприклад, на рис. 3 побудована у функції часу друга гармоніка спектра з частотою
повністю визначають параметри цієї гармоніки. Наприклад, на рис. 3 побудована у функції часу друга гармоніка спектра з частотою ![]() , амплітудою
, амплітудою ![]() і зсувом максимуму косинусоїди вправо (відносно
і зсувом максимуму косинусоїди вправо (відносно ![]() ) на відрізок часу пропорційний
) на відрізок часу пропорційний ![]() .
.
Оскільки середня потужність періодичного сигналу є сумою потужностей гармонічних складових сигналу і потужності сталої складової, ширина спектра визначається частотою коливання з амплітудою ![]() , яка ще впливає на значення середньої потужності на заданому рівні:
, яка ще впливає на значення середньої потужності на заданому рівні:
![]() .
.
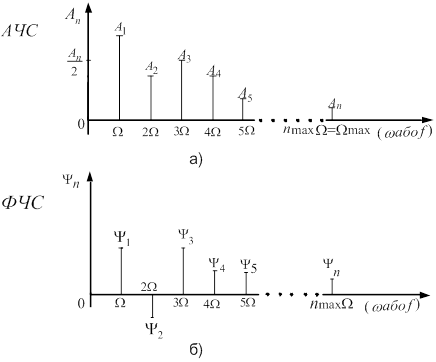
Рисунок 2 – Графіки АЧС (а) і ФЧС (б)
У тих випадках, коли ![]() – парна функція часу,
– парна функція часу, ![]() в (1) дорівнює нулю або
в (1) дорівнює нулю або ![]() . Для непарної функції, навпаки, ряд Фур’є складається тільки із синусоїдних коливань, тобто
. Для непарної функції, навпаки, ряд Фур’є складається тільки із синусоїдних коливань, тобто ![]() дорівнює
дорівнює ![]() або
або ![]() .
.
У двох послідовностях імпульсів ![]() і
і ![]() , які відрізняються тільки початком відліку часу, АЧС однакові, а відрізняються тільки їх ФЧС. Дійсно, якщо
, які відрізняються тільки початком відліку часу, АЧС однакові, а відрізняються тільки їх ФЧС. Дійсно, якщо ![]() , тоді
, тоді
![]() (2)
(2)
Таким чином, при зсуві сигналу на ![]() фази його гармоніки змінюється на
фази його гармоніки змінюється на ![]() .
.
Як ілюстрації наведемо результати розкладу в ряд Фур’є періодичної послідовності прямокутних імпульсів (рис. 4), яку аналітично можна записати у вигляді:
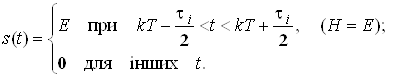
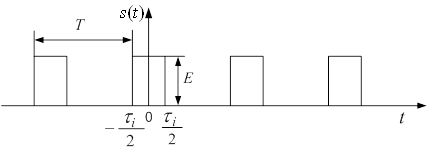
Рисунок 4 – Періодична послідовність прямокутних імпульсів
На підставі (2) ![]() можна подати у вигляді:
можна подати у вигляді:
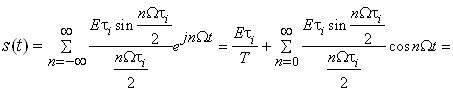
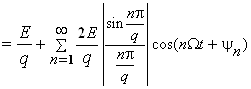 . (3)
. (3)
Обвідна амплітуд спектра визначається значеннями функції:
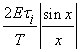 ,
,
де 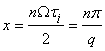 , при
, при ![]() , тобто
, тобто  ,
, ![]() і амплітуди гармонік дорівнюють нулю.
і амплітуди гармонік дорівнюють нулю.
Позитивним значенням ![]() відповідають нульові значення фаз гармонік, від’ємним – початкові фази рівні
відповідають нульові значення фаз гармонік, від’ємним – початкові фази рівні ![]() , тому що
, тому що ![]() , тобто початкові фази гармонік у (3) визначаються як:
, тобто початкові фази гармонік у (3) визначаються як:
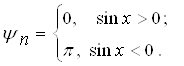
Графіки АЧС і ФЧС наведено на рис. 5 Графіки побудовано для щільності ![]() . Такі спектри мають назву дискретних.
. Такі спектри мають назву дискретних.
При змінюванні тривалості імпульсів або частоти їх повторення змінюються і спектри. Рис. 6 ілюструє зміни у спектрах при збільшенні тривалості імпульсів ![]() і незмінній частоті повторення
і незмінній частоті повторення ![]() . При збільшенні тривалості імпульсів відбувається «стиснення» спектра – гармонічні складові, які мають найбільші амплітуди, зсуваються в область більш низьких частот. Інтервали між спектральними лініями за частотою не змінюються.
. При збільшенні тривалості імпульсів відбувається «стиснення» спектра – гармонічні складові, які мають найбільші амплітуди, зсуваються в область більш низьких частот. Інтервали між спектральними лініями за частотою не змінюються.
Рис. 7 ілюструє зміни у спектрах при збільшенні періоду і незмінній тривалості імпульсу. Збільшення періоду (зменшення частоти слідування) призводить до зменшення інтервалу між спектральними лініями. При цьому зменшується і амплітуда всіх складових спектра, що фізично пояснюється зменшенням потужності у періодичної послідовності імпульсів.
Якщо спрямувати період до нескінченності, амплітуди зменшаться до нескінченно малих величин, а спектральні лінії наблизяться одна до одної, тобто спектр стане суцільним. Відбудеться перехід від періодичної послідовності до одиночного імпульсу.
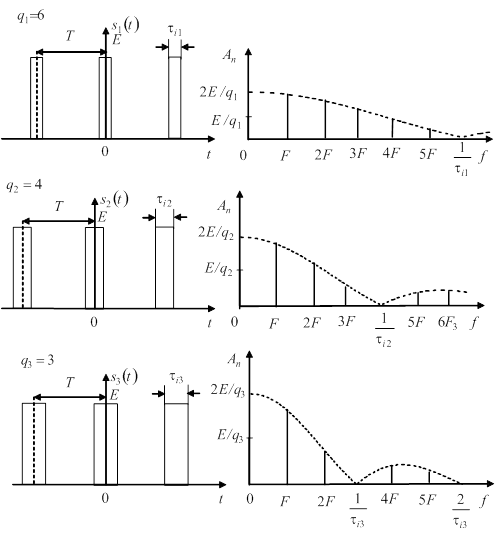
Рисунок 6 – Вплив тривалості імпульсів на АЧС
Якщо початок відліку часу не збігається з серединою імпульсів (рис. 8,а), відповідно до формули (3) змінюється тільки ФЧС, як показано на рис. 8,б.
Спектри неперіодичних одиночних сигналів оцінюється, так званою, спектральною густиною ![]() , у відповідності з перетворенням Фур’є:
, у відповідності з перетворенням Фур’є:
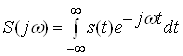 .
.
Модуль спектральної густини має розмірність В/Гц або А/Гц в залежності від розмірності сигналу (В або А).
Відновлення одиночного сигналу за його спектральною густиною виконується за допомогою оберненого перетворення Фур’є:
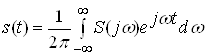 .
.
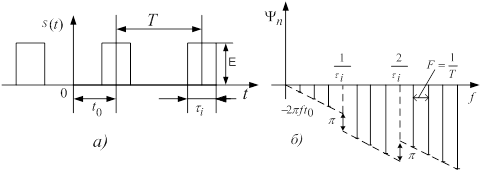
Рисунок 8 – Вплив початку відліку часу на ФЧС
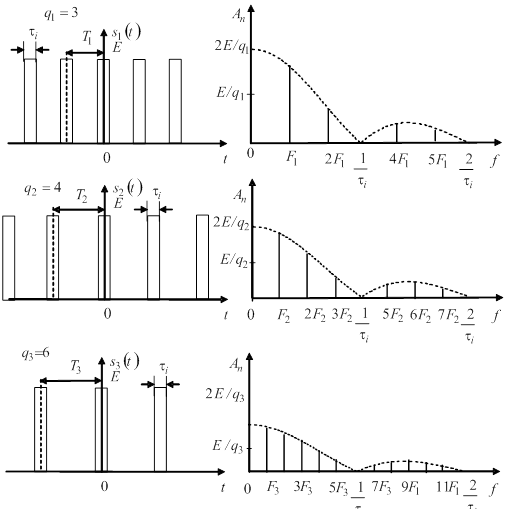
Спектральна густина одиночного прямокутного імпульсу висотою ![]() і тривалістю
і тривалістю ![]() описується виразом:
описується виразом:
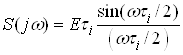 .
.
Частотна залежність модуля спектральної густини ![]() (АЧС) і частотна залежність аргументу спектральної густини
(АЧС) і частотна залежність аргументу спектральної густини ![]() (ФЧС) одиночного прямокутного імпульсу наведені на рис. 9.
(ФЧС) одиночного прямокутного імпульсу наведені на рис. 9.
Для розрахунку відгук кіл спектральним методом використовують комплексний коефіцієнт передачі кола ![]() , який дозволяє визначити вихідні сигнали у випадках:
, який дозволяє визначити вихідні сигнали у випадках:
а) періодичного сигналу –
![]()
періодичний послідовність імпульс спектр амплітуда
де ![]() ,
, ![]() ,
,![]() – комплексна амплітуда, амплітуда і початкова фаза
– комплексна амплітуда, амплітуда і початкова фаза ![]() -ї гармоніки вхідного сигналу відповідно;
-ї гармоніки вхідного сигналу відповідно; ![]() ,
, ![]() ,
, ![]() – комплексний коефіцієнт передачі, значення АЧХ і ФЧХ кола для частоти
– комплексний коефіцієнт передачі, значення АЧХ і ФЧХ кола для частоти ![]() -ї гармоніки вхідного сигналу відповідно;
-ї гармоніки вхідного сигналу відповідно;
б) неперіодичного сигналу –
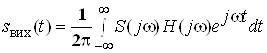 ,
,
де ![]() – спектральна густина вхідного сигналу.
– спектральна густина вхідного сигналу.
Розглянуті вище сигнали мають спектри в області низьких частот і такі сигнали називають відеосигналами. На відміну від них, радіосигнали з амплітудною, частотною або фазовою модуляцією мають спектри, сконцентровані поблизу носійної частоти ![]() .
.
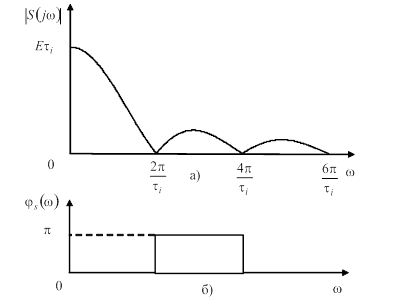
Рисунок 9 – АЧС (а) і ФЧС (б) одиночного прямокутного імпульсу наведеного на рис. 8,а
Якщо у носійного коливання ![]() , амплітуда змінюється за законом
, амплітуда змінюється за законом ![]() відносно деякого середнього рівня
відносно деякого середнього рівня ![]() , формується амплітудно-модульоване коливання (АМК), яке можна записати у вигляді:
, формується амплітудно-модульоване коливання (АМК), яке можна записати у вигляді:
![]() ,
,
де постійний коефіцієнт ![]() вибраний таким, щоб амплітуда коливань була завжди додатною.
вибраний таким, щоб амплітуда коливань була завжди додатною.
Якщо модулююче коливання ![]() містить декілька гармонічних складових, які подані рядом:
містить декілька гармонічних складових, які подані рядом:
![]() , (4)
, (4)
тоді модульоване коливання набуває вигляду:
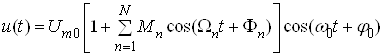 , (5)
, (5)
де величини ![]() – парціальні (часткові) коефіцієнти модуляції,
– парціальні (часткові) коефіцієнти модуляції, ![]() .
.
Подамо модулюючий сигнал (4) в іншому вигляді, пронормувавши амплітуди гармонік за амплітудою першої гармоніки.
![]() ,
,
де 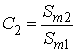 ;
; 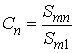 – нормовані амплітуди гармонік.
– нормовані амплітуди гармонік.
Тоді у виразі (5) парціальний коефіцієнт модуляції ![]() -ї гармоніки можна подати як:
-ї гармоніки можна подати як:
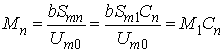 .
.
Спектр АМК (1) після тригонометричних перетворень набуває вигляду
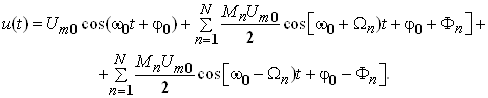 (6)
(6)
Якщо АЧС модулюючого коливання має вигляд, наведений на рис. 2, а), тоді у відповідності до (2) матимемо спектр АМК, представлений на рис. 10.
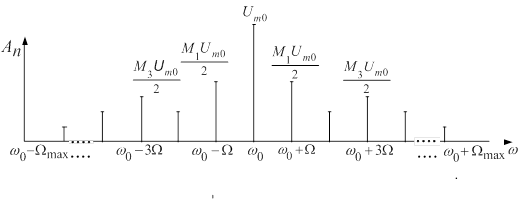
Рисунок 10 – АЧС амплітудно-модульованого коливання
Таким чином, спектр АМК можна подати як перенесений на носійну частоту спектр модулюючого відеосигналу. Спектр містить носійне коливання і дві бокові смуги частот – «нижню» з частотами ![]() і «верхню» з частотами
і «верхню» з частотами ![]() . Рівень бокових частот визначається відповідними коефіцієнтами глибини модуляції
. Рівень бокових частот визначається відповідними коефіцієнтами глибини модуляції ![]() , а ширина спектра дорівнює
, а ширина спектра дорівнює ![]() . Такий спектр відповідає радіосигналу.
. Такий спектр відповідає радіосигналу.
Частковим випадком АМК є балансна модуляція або амплітудна маніпуляція, коли радіосигнал отримуємо у вигляді:
![]() .
.
При цьому у випадку модулюючого сигналу ![]() з дискретним спектром (4) спектр радіосигналу (2) відрізнятиметься відсутністю носійного коливання.
з дискретним спектром (4) спектр радіосигналу (2) відрізнятиметься відсутністю носійного коливання.
У випадку, коли балансна модуляція здійснюється неперіодичним сигналом, спектральна густина радіосигналу має вид:
![]() ,
,
де ![]() – спектральна густина модулюючого відеосигналу.
– спектральна густина модулюючого відеосигналу.
Наприклад, спектральна густина радіосигналу на разі модулюючого коливання у вигляді одиночного прямокутного радіоімпульсу за умов балансної модуляції описується виразом:
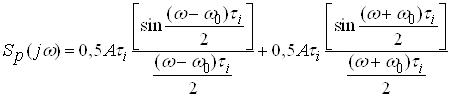 .
.
Таким чином, амплітудна маніпуляція одиночним сигналом призводить до переносу спектра модульованого сигналу в область частот ![]() .
.
Наявність від’ємних частот при спектральному аналізі пояснюється комплексною формою запису ряду Фур’є, або інтеграла Фур’є, в яких дійсна змінна часу коливання ![]() формується за допомогою векторів, що обертаються як у додатному напрямі з частотою
формується за допомогою векторів, що обертаються як у додатному напрямі з частотою ![]() , так і у від’ємному з частотою
, так і у від’ємному з частотою ![]() .
.