Задачі математичного програмування
Завдання 2
Записати двоїсту задачу до поставленої задачі лінійного програмування. Розв’язати одну із задач симплексним методом і визначити оптимальний план іншої задачі. Оптимальні результати перевірити графічно.
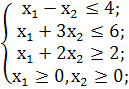
![]()
Розв’язок
Розв’яжемо задачу лінійного програмування симплексним методом.
Визначимо мінімальне значення цільової функції F(X) = 4x1+2x2 при наступних умовах-обмежень.
x1-x2≤4
x1+3x2≤6
x1+2x2≥2
Для побудови першого опорного плану систему нерівностей приведемо до системи рівнянь шляхом введення додаткових змінних.
Оскільки маємо змішані умови-обмеження, то введемо штучні змінні x.
1x1-1x2 + 1x3 + 0x4 + 0x5 = 4
1x1 + 3x2 + 0x3 + 1x4 + 0x5 = 6
1x1 + 2x2 + 0x3 + 0x4-1x5 = 2
Для постановки задачі на мінімум цільову функцію запишемо так:
F(X) = 4x1+2x2 - Mx6 => max
Вважаючи, що вільні змінні рівні 0, отримаємо перший опорний план:
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | х6 |
| 0 | х3 | 4 | 1 | -1 | 1 | 0 | 0 | 0 |
| x4 | 6 | 1 | 3 | 0 | 1 | 0 | 0 | |
| х6 | 2 | 1 | 2 | 0 | 0 | -1 | 1 | |
| Індексний рядок | F(X0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Переходимо до основного алгоритму симплекс-методу.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 1 | x3 | 4 | 1 | -1 | 1 | 0 | 0 | 0 | 0 |
| x4 | 6 | 1 | 3 | 0 | 1 | 0 | 0 | 2 | |
| x6 | 2 | 1 | 2 | 0 | 0 | -1 | 1 | 1 | |
| Індексний рядок | F(X1) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Оскільки, в індексному рядку знаходяться негативні коефіцієнти, поточний опорний план неоптимальний, тому будуємо новий план. У якості ведучого виберемо елемент у стовбці х2, оскільки значення коефіцієнта за модулем найбільше.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 2 | x3 | 5 | 1.5 | 0 | 1 | 0 | -0.5 | 0.5 | 3.33 |
| х4 | 3 | -0.5 | 0 | 0 | 1 | 1.5 | -1.5 | 0 | |
| x2 | 1 | 0.5 | 1 | 0 | 0 | -0.5 | 0.5 | 2 | |
| Індексний рядок | F(X2) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Даний план, також не оптимальний, тому будуємо знову нову симплексну таблицю. У якості ведучого виберемо елемент у стовбці х2.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 3 | x3 | 2 | 0 | -3 | 1 | 0 | 1 | -1 | 2 |
| X4 | 4 | 0 | 1 | 0 | 1 | 1 | -1 | 4 | |
| X1 | 2 | 1 | 2 | 0 | 0 | -1 | 1 | 0 | |
| Індексний рядок | F(X3) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min | |||||
| 4 | х5 | 2 | 0 | -3 | 1 | 0 | 1 | -1 | 0 | |||||
| X4 | 2 | 0 | 4 | -1 | 1 | 0 | 0 | 0.5 | ||||||
| X1 | 4 | 1 | -1 | 1 | 0 | 0 | 0 | 0 | ||||||
| Індексний рядок | F(X4) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | х6 | ||||||
| 5 | х5 | 3.5 | 0 | 0 | 0.25 | 0.75 | 1 | -1 | ||||||
| х2 | 0.5 | 0 | 1 | -0.25 | 0.25 | 0 | 0 | |||||||
| х1 | 4.5 | 1 | 0 | 0.75 | 0.25 | 0 | 0 | |||||||
| Індексний рядок | F(X5) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||
Оптимальний план можна записати так:
x5 = 3.5
x2 = 0.5
x1 = 4.5
F(X) = 4*4.5 + 2*0.5 = 19
Складемо двоїсту задачу до поставленої задачі лінійного програмування.
y1+y2+y3≥4
-y1+3y2+2y3≥2
4y1+6y2+2y3 => min
y1 ≥ 0
y2 ≥ 0
y3 ≤ 0
Рішення двоїстої задачі дає оптимальну оцінок ресурсів. Використовуючи останню інтиграцію прямої задачі знайдемо,оптимальний план двоїстої задачі. Із теореми двоїстості слідує, що Y = C*A-1.
Сформуємо матрицю A із компонентів векторів, які входять в оптимальний базис.
Визначивши обернену матрицю А-1 через алгебраїчне доповнення, отримаємо:
Як видно із останнього плану симплексної таблиці, обернена матриця A-1 розміщена у стовбцях додаткових змінних.
Тоді Y = C*A-1 =
Запишемо оптимальний план двоїстої задачі:
y1 = 2.5
y2 = 1.5
y3 = 0
Z(Y) = 4*2.5+6*1.5+2*0 = 19
Завдання 3
Розвязати транспортну задачц.
| 1 | 2 | 4 | 1 | 5 | 200 |
| 1 | 2 | 1 | 3 | 1 | 120 |
| 2 | 1 | 3 | 3 | 1 | 150 |
| 100 | 90 | 200 | 30 | 80 |
Подобные работы: