Реконструкция значений утраченных точек изображений по энтропии коэффициентов дискретного косинусного преобразования

Оценивать истинные значения пикселей изображений в той или иной степени необходимо в большинстве задач цифровой обработки изображений. Например, задача устранения импульсного шума на изображении может решаться в два этапа. На первом этапе все пиксели изображения классифицируются на искаженные и не искаженные импульсным шумом. После этого на втором этапе каким-либо образом оцениваются истинные значения пикселей, искаженных импульсным шумом. При нахождении каждой такой оценки тем или иным образом учитываются значения известных близлежащих пикселей.

Другой типичной задачей, в которой требуется оценить значения неизвестных пикселей, является задача реконструкции утерянных участков изображений (групп пикселей).

В целом ряде задач, таких как подавление аддитивного или мульти-пликативного шума, восстановление изображений, масштабирование, также приходится оценивать истинные значения искаженных пикселей изображений.

Для оценки значения заданного пикселя по известным значениям близлежащих пикселей используют фильтры, сплайны, различные предсказатели, триангуляцию Делоне, различные комбинированные методы. Здесь предлагается новый подход, основанный на том предположении, что истинное значение пикселя минимизирует энтропию коэффициентов дискретного косинусного преобразования (ДКП) блока изображения, которому данный пиксель принадлежит.

В разделе 2 подробно описывается идея предлагаемого подхода. В разделах 3 и 4 анализируется эффективность предлагаемого подхода в сравнении с новым и одним из лучших методов, основанном на сохраняющих кривые частичных дифференциальных уравнениях (CPPDE). В разделе 3 рассматривается задача устранения импульсного шума, а в разделе 4 – задача реконструкции утерянных участков изображений.

1. основная идея

Как известно, ДКП хорошо декоррелирует значения пикселей блока изображения, для которого оно осуществляется (1), другими словами, минимизирует значение энтропии в этом блоке при заданном шаге квантования (ШК). Именно поэтому ДКП широко используется в сжатии изображений (стандарт JPEG) и сжатии видео (семейство стандартов MPEG, стандарт H.264 и др.). Чтобы понять, как этот факт можно использовать при реконструкции утерянных пикселей изображения, рассмотрим подробнее, что представляют собой коэффициенты ДКП какого-либо блока изображения.

Коэффициенты ДКП для естественных фотографических изображений (кроме коэффициентов с индексом (0,0), соответствующих средним уровням блоков) распределены по обобщенному Гауссовскому закону распределения:

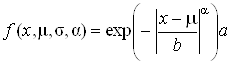,                                                        (1)

где ,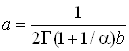

 – математическое ожидание,  – параметр, связанный с дисперсией, Γ(∙) – гамма-функция, x – значение коэффициента ДКП. Значение =2 соответствует нормальному закону распределения, =1 соответствует Лаплассовскому закону распределения. Энтропия коэффициента x может быть оценена как

.                                                             (2)

На рис. 1 приведено обобщенное Гауссовское распределение для α=0,5, а на рис. 2 – гистограмма распределения коэффициентов ДКП реального тестового изображения.

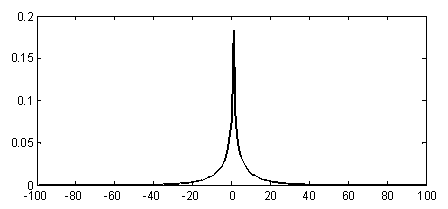
Рис. 1 Обобщенное Гауссовское распределение, =0,5, =0, =15

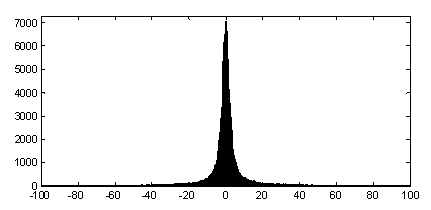
Рис. 2. Гистограмма значений коэффициентов ДКП блоков 8×8 пикселей тестового изображения Barbara при ШК=1

Как видно, приведенные на рис. 1 и 2 распределения достаточно похожи.

На рис. 3 приведен график энтропии данных, имеющих обобщенное Гауссовское распределение с рис. 1, а на рис. 4 – графики энтропии для квантованных коэффициентов реальных изображений.

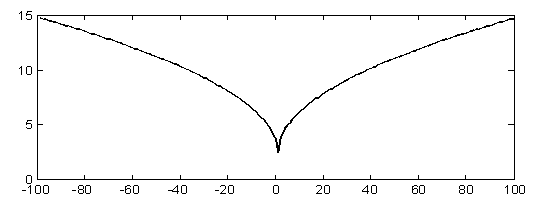
Рис. 3. Энтропия данных, имеющих распределение, как на рис. 1

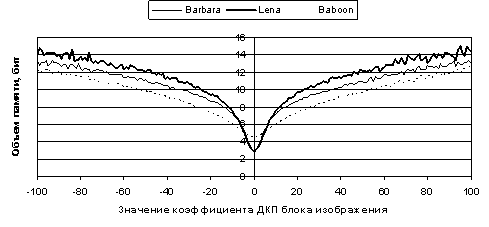
Рис. 4. Энтропия коэффициентов ДКП тестовых изображений Barbara, Lena и Baboon для ШК=1

Как видно из рис. 4, графики энтропии для реальных изображений являются подобными, но не идентичными друг другу. Для точной оценки их формы нужно знать параметры  и  для заданного изображения, определение которых является достаточно сложной задачей, особенно для изображений, искаженных импульсным шумом.

На рис. 5 приведены графики энтропии коэффициентов ДКП для одного и того же изображения, но при разных шагах квантования.

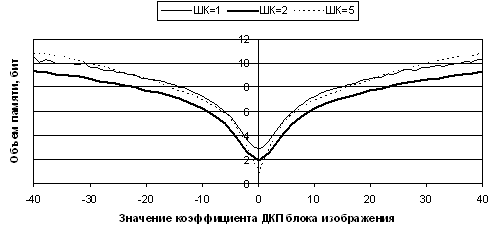
Рис. 5. Энтропия коэффициентов ДКП изображения для разных ШК

На примере графиков, приведенных на рис. 4 и 5, показано, что зависимость энтропии от значения коэффициента ДКП является разной как для различных изображений, так и для одного и того же изображения, но для разных шагов квантования. В то же время форма этих зависимостей и их параметры отличаются не очень существенно и могут быть для простоты вычислений приближенно аппроксимированы, например, функцией, приведенной на рис. 6.

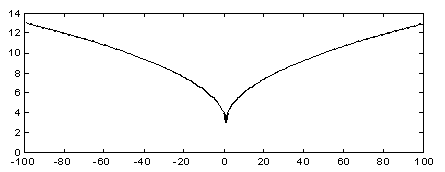
Рис. 6. График функции

Что же происходит с законом распределения и энтропией коэффициентов ДКП при искажении изображения, например, импульсным шумом? Гистограмма значений коэффициентов ДКП существенно изменяется (рис. 7 в сравнении с рис. 2), а суммарная энтропия коэффициентов ДКП резко возрастает (см. рис. 8).

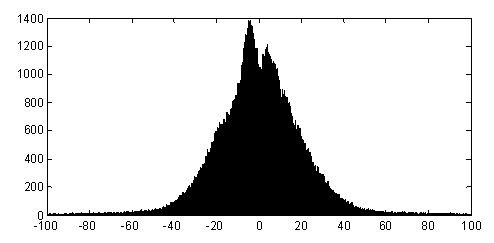
Рис. 7. Гистограмма значений коэффициентов ДКП тестового изображения Barbara для ШК=1, если один пиксель каждого блока изображения искажен шумом типа «перец» (значение 0) (1)

Рис. 8. Энтропия коэффициентов ДКП тестового изображения Barbara при ШК=1 для импульсного шума с вероятностями 0, 3 и 10 %

Собственно, так как ДКП минимизирует энтропию в блоке изображения, то внесение любых случайных искажений будет приводить к ее повышению, а задача нахождения истинных (неискаженных) значений утерянных пикселей сводится к такому изменению значения утраченного пикселя (или группы пикселей), которое приведет к минимизации суммарной энтропии коэффициентов ДКП блока.

Основная идея предлагаемого подхода – за счет варьирования значения заданного пикселя попытаться минимизировать энтропию коэффициентов DCT в блоке изображения и, таким образом, найти истинное значение этого пикселя. При этом, уменьшение модулей коэффициентов, близких к нулю, будет иметь большее значение, чем уменьшение коэффициентов с большими значениями модулей. В результате такой минимизации энтропии будут подавлены (уменьшены) в основном коэффициенты, близкие к нулю, а информационная часть коэффициентов, сосредоточенная в длинных хвостах гистограммы, останется без больших изменений.

При вычислении суммарной энтропии коэффициентов ДКП блоков можно воспользоваться выражениями (1) и (2), но вычислительно проще аппроксимировать их функцией, приведенной на рис. 6. При этом, целевая функция, которую нужно минимизировать для какого-то блока изображения, примет вид:

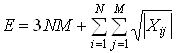,                                                                   (3)

где X_ij – значение ij-го коэффициента DCT блока; N и M – размеры блока изображения.

Для минимизации функции E для заданной точки можно либо перебрать все возможные значения этой точки от 0 до 255, либо воспользоваться одним из численных методов оптимизации.

Отметим, что для любой заданной точки изображения и заданных размеров блока расположение блока с заданной точкой внутри него можно выбирать несколькими способами (рис. 9).