Классический метод наименьших квадратов
Алтайский институт труда и права (филиал)
Академии труда и социальных отношений
Финансово-экономический факультет
КОНТРОЛЬНАЯ РАБОТА
по дисциплине Эконометрика
на тему
Классический метод наименьших квадратов
Студента 3 курса 681 группы
Бахтеевой Татьяны Михайловны
2010
Метод наименьших квадратов (МНК) – один из наиболее широко используемых методов при решении многих задач восстановления регрессионных зависимостей(1). Впервые МНК был использован Лежандром в 1806 г. для решения задач небесной механики на основе экспериментальных данных астрономических наблюдений. В 1809 г. Гаусс изложил статистическую интерпретацию МНК и тем самым дал начало широкого применения статистических методов при решении задач восстановления регрессионных зависимостей. Строгое математическое обоснование и установление границ содержательной применимости метода наименьших квадратов даны А.А. Марковым и А.Н. Колмогоровым. Ныне способ представляет собой один из важнейших разделов математической статистики и широко используется для статистических выводов в различных областях науки и техники.
Приведу краткое описание данного метода. Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки. Применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений. В настоящее время широко применяется при обработке количественных результатов естественнонаучных опытов, технических данных, астрономических и геодезических наблюдений и измерений.
Можно выделить следующие достоинства метода:
а) расчеты сводятся к механической процедуре нахождения коэффициентов;
б) доступность полученных математических выводов.
Основным недостатком МНК является чувствительность оценок к резким выбросам, которые встречаются в исходных данных.
Рассмотрю применение классического метода наименьших квадратов для нахождения неизвестных параметров уравнения регрессии на примере модели линейной парной регрессии. Пусть подобрана эмпирическая линия, по виду которой можно судить о том, что связь между независимой переменной и зависимой переменной линейна и описывается равенством:
(1)
Необходимо найти такие значения параметров 
и 
, которые бы доставляли минимум функции (1), т. е. минимизировали бы сумму квадратов отклонений наблюдаемых значений результативного признака 
от теоретических значений 
(значений, рассчитанных на основании уравнения регрессии):
(2)
При минимизации функции (1) неизвестными являются значения коэффициентов регрессии 
и 
Значения зависимой и независимой переменных известны из наблюдений.
Для того чтобы найти минимум функции двух переменных, нужно вычислить частные производные этой функции по каждой из оцениваемых параметров и приравнять их к нулю. В результате получаем стационарную систему уравнений для функции (2):
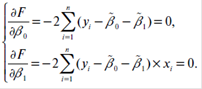
регрессивный оценка обработка результат
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему:
Эта система нормальных уравнений относительно коэффициентов 
и 
для зависимости
Решением системы нормальных уравнений являются оценки неизвестных параметров уравнения регрессии и :
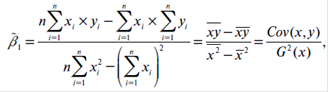
Где 
- среднее значение зависимого признака;
- среднее значение независимого признака;
- среднее арифметическое значение произведения зависимого и независимого признаков;
- дисперсия независимого признака;
- ковариация между зависимым и независимым признаками.
Рассмотрим применение МНК на конкретном примере.
Имеются данные о цене на нефть 
(долларов за баррель) и индексе акций нефтяной компании 
(в процентных пунктах). Требуется найти эмпирическую формулу, отражающую связь между ценой на нефть и индексом акций нефтяной компании исходя из предположения, что связь между указанными переменными линейна и описывается функцией вида
Зависимой переменной 
в данной регрессионной модели будет являться индекс акций нефтяной компании, а независимой 
- цена на нефть.
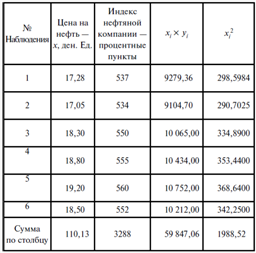
Для нахождения коэффициентов 
и 
построим вспомогательную таблицу (1).
Таблица 1.
Таблица для нахождения коэффициентов 
и 
Запишем систему нормальных уравнений исходя из данных таблицы:
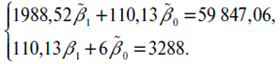
Решением данной системы будут следующие числа:
Таким образом, уровень регрессии, описывающее зависимость между ценой на нефть и индексом акций нефтяной компании, можно записать как:
На основании полученного уравнения регрессии можно сделать вывод о том, что с изменением цены на нефть на 1 денежную единицу за баррель индекс акций нефтяной компании изменяется примерно на 15, 317 процентных пункта.
Метод наименьших квадратов является наиболее распространенным методом оценивания параметров уровня регрессии, и применим только для линейных относительно параметров моделей или приводимых к линейным с помощью преобразования и замены переменных(2).
Список использованной литературы:
1. Крянев А.В. Применение современных методов математической статистики при восстановлении регрессионных зависимостей на ЭВМ. Учебное пособие. М.: 1988. С. 4.
2. Мамаева З.М. Математические методы и модели в экономике. ч 2. Учебное пособие. Н. Новгород.: 2010. С 17
3. Эконометрика. Конспект лекций. Яковлева А.В. М.: Эксмо, 2008.С. 126.