Фильтрование воды
Сущность процесса, классификация фильтров по принципу действия
В подавляющем большинстве технологических схем водоподготовки завершающим процессом является фильтрование, в ходе которого из воды извлекаются не только дисперсии, но и коллоиды. В этом состоит отличие метода фильтрования от всех методов предварительной очистки воды.
Сущность метода заключается в фильтровании обрабатываемой воды, содержащей примеси, через фильтрующий материал, проницаемый для жидкости и непроницаемый для твердых частиц. При этом процесс сопровождается значительными затратами энергии. Однако, допускать большие потери напора в технике водоочистки можно лишь при обработке небольших количеств воды. Это определяет место фильтровальных сооружений в технологической схеме, т. е. в большинстве случаев фильтрование является завершающим этапом обработки воды и производится после ее предварительного осветления в отстойниках, флотаторах или осветлителях.
При пропуске воды через слой зернистого материала в зависимости от заряда и соотношения размеров примесей воды и зерен фильтрующей загрузки может происходить три вида фильтрования:
1) задержание примесей на поверхности фильтрующего слоя (пленочное фильтрование) описываемое формулой Хазена δ = 0,01 (v*d3)0.5, где δ — диаметр наименьших задерживаемых частиц, мм; d3 — эффективный диаметр зерен загрузки, мм; v — скорость фильтрования до 10 м/ч;
2) задержание примесей в порах фильтрующего слоя (объемное фильтрование);
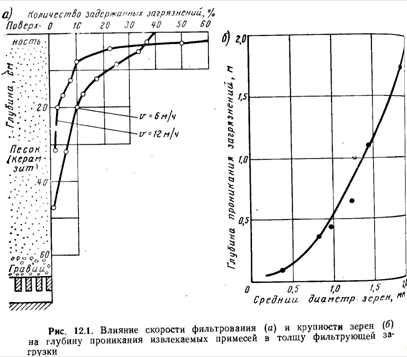
3) одновременное образование примесями пленки и их отложение в порах загрузки. В большинстве случаев на современных фильтрах пленка не образуется и примеси вместе с водой проникают в толщу фильтрующего слоя, при этом глубинa проникновения загрязнений в толщу загрузки тем больше, чем больше скорость фильтрования, крупнее зерна фильтрующего слоя и чем меньше размеры частиц взвеси, извлекаемых из воды (рис. 12.1). Пленочное фильтрование лежит в основе работы медленных фильтров. Это процесс чисто механического извлечения из воды диспергированных примесей. В основе объемного фильтрования лежит предварительное коагулирование примесей воды с целью уменьшения или ликвидации их заряда. Так как при обычных значениях рН исходной воды поверхность зерен фильтрующего материала и частицы примесей воды несут отрицательный заряд, взвесь в порах фильтрующего слоя задерживается плохо. Следовательно, в основе объемного фильтрования лежат процессы адгезии скоагулированных примесей на поверхности зерен фильтрующего слоя и суффозии, т. е. отрыва ранее прилипших частиц и переноса их гидродинамическими силами потока в нижние слои загрузки.
Водоочистные сооружения, на которых осуществляется процесс фильтрования, называют фильтрами. Фильтры по виду фильтрующей среды делят на тканевые или сетчатые, каркасные или намывные (диатомовые), зернистые (песчаные, керамзитовые и др.). Из вышеперечисленных трех групп фильтров наиболее значительной является последняя. Фильтры этой группы в технике водоснабжения применяют наиболее широко. фильтры с зернистой загрузкой можно классифицировать по ряду основных признаков: 1) по скорости фильтрования — медленные (0,1 ... 0,3 м/ч), скорые (5... 12 м/ч) и сверхскоростные (36... 100 м/ч); 2) по давлению, под которым они работают, — открытые (или безнапорные) и напорные, 3) по направлению фильтрующего потока — однопоточные (обычные скорые фильтры), двухпоточные (фильтры АКХ, ДДФ), многопоточные; 4) по крупности фильтрующего материала — мелко-, средне- и крупнозернистые; 5) по количеству фильтрующих слоев — одно-, двух- и многослойные. Устройство открытого скорого фильтра площадью до 30 м2 показано на рис. 12.2. Прошедшая предочистку вода поступает в боковой карман, а из него — в резервуар фильтра. Высота слоя воды над поверхностью загрузки должна быть не менее 2 м. В процессе фильтрования вода проходит фильтрующий и поддерживающий слои, а затем поступает в распределительную систему и далее в резервуар чистой воды. Максимальная потеря напора в фильтрующей загрузке допускается 3 ... 3,5 м. Во время промывки фильтра промывная вода подается в распределительную систему и далее снизу вверх в фильтрующий слой, который она расширяет (взвешивает). Дойдя до верхней кромки промывных желобов, промывная вода вместе с вымытыми ею из фильтрующего материала загрязнениями переливается в желоба, а из них в боковой карман и отводится на сооружения оборота промывной воды.
Расчетную скорость фильтрования f = 6 ... 10 м/ч, толщину слоя однослойной фильтрующей загрузки h = 0,7 ... 2,0 м, продолжительность 5 ... 7 мин и интенсивность промывки ш=12... 18 л./(с*м2) принимают в соответствии со СНиПом в зависимости от крупности зерен фильтрующей загрузки 0,5 ... 2,0 мм. Фильтрующий слой выполняют из отсортированного зернистого материала, удовлетворяющего санитарным требованиям в обладающего достаточной химической стойкостью и механической прочностью (кварцевый песок, дробленый антрацит, горелые породы, керамзит, керамическая крошка, доменные шлаки, Дробленый мрамор, полимеры и др.). Поддерживающий слой из гравия или щебня высотой 0,45…0,55 с крупностью зерен 2…40 мм, на котором лежит фильтрующая загрузка, укладывают для того, чтобы мелкий фильтрующий материал не вымывался из фильтрующего слоя и не уносился вместе с фильтруемой водой через отверстия распределительной системы. Недостатком поддерживающих слоев является возможность их смещения при промывке, что нарушает их горизонтальность и в конечном счете нарушает работу фильтра. Распределительная (дренажная) система является важным элементом фильтра. Она должна собирать и отводить профильтрованную воду без выноса зерен фильтрующего материала ц при промывке равномерно распределять промывную воду по площади фильтра. В настоящее время повсеместно применяют распределительные системы большого сопротивления. Равномерность распределения промывной воды по площади в таких системах достигается вследствие большого сопротивления движению воды через проходные отверстия.
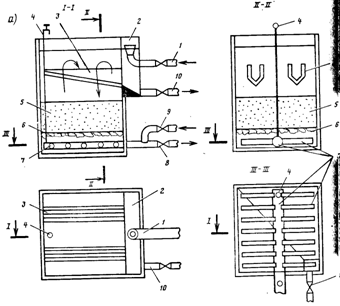
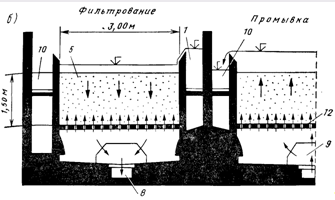
Рис. 12.2. Схема открытого (безнапорного) скорого фильтра с боковым карманом (а) и боковым отводом промывной воды (б).
7 — распределительная система: магистральная труба (или канал) и перфорированные ответвления; 6 — поддерживающий слой гравия (щебня); 5 — фильтрующая загрузка (кварцевый песок, керамзит, шунгизит и др.); 3 — водосборные желоба; 4 — воздушник; 2 — боковой карман; 1, 8 — подача исходной воды и отвод фильтрата; 9, 10 — подача и отвод промывной воды; 11 — водосток; 12 — колпачковая распределительная (дренажная) система.
Промывка скорых фильтров производится обратным током профильтрованной воды путем ее подачи под напором в поддонное пространство или в дренажную трубчатую систему. Промывная вода, проходя со скоростью, в 7 ... 10 раз большей, чем скорость фильтрования, через фильтрующую загрузку снизу вверх, поднимает и взвешивает ее. Зерна расширившегося песка, хаотично двигаясь, соударяются друг с другом, при этом налипшие на них загрязнения оттираются и попадают в промывную воду, которая собирается и удаляется сборными желобами, расположенными над поверхностью фильтрующей загрузки, в водосток. Желоба располагают на такой высоте Нж, чтобы в них попадали только вымытые из песка загрязнения, но не песок.
Теоретические основы очистки воды фильтрованием через зернистые материалы
Из известных теорий процесса очистки воды фильтрованием наибольшее признание получила теория Д. М. Минца, которая экспериментально подтверждена и внедрена. На основе этой теории разработана методика технологического анализа процесса фильтрования, позволяющая определять параметры процесса и использовать их для оптимизации режима работы фильтровальных сооружений.
Согласно теории Д. М. Минца, при движении воды, содержащей взвешенные частицы, через зернистую загрузку фильтровальных аппаратов последние задерживаются загрузкой и вода осветляется. Одновременно в толще загрузки накапливаются загрязнения, вследствие чего уменьшается свободный объем пор, увеличивается гидравлическое сопротивление загрузки. Возрастание гидравлического сопротивления приводит к росту потери напора в загрузке.
Извлечение примесей из воды и их закрепление на зернах фильтрующей загрузки происходит под действием сил адгезии. Осадок, накапливающийся в загрузке из задержанных примесей, имеет весьма непрочную структуру. Под влиянием гидродинамических сил потока эта структура разрушается и некоторая часть ранее прилипших частиц отрывается от зерен загрузки в виде мелких хлопьев и переносится в последующие слои загрузки (суффозия), где вновь задерживается в поровых каналах. Следовательно, осветление воды в зернистой загрузке следует рассматривать как суммарный результат двух противоположных процессов: процесса адгезии и процесса суффозии. Осветление воды в каждом элементарном слое загрузки происходит до тех пор, пока интенсивность прилипания частиц превышает интенсивность их отрыва. По мере накопления осадка интенсивность отрыва частиц увеличивается. Кинетика прилипания и отрыва частиц определяет ход процесса осветления воды по толщине слоя фильтрующей загрузки и во времени (рис. 12.3, где показаны кривые изменения концентрации взвеси в воде по высоте загрузки). Каждая кривая относится к определенному моменту времени. Кривая 1 характерна для начального периода процесса после того, как первые порции фильтруемой воды пройдут через слой загрузки, а кривая 4 — предельному насыщению загрузки осадком. Кривая 1 показывает, как изменяется концентрация взвеси в воде по высоте загрузки толщиной ха только под действием сил прилипания.
По мере накопления осадка в загрузке явление отрыва ранее прилипших частиц начинает проявляться все более заметно. Характер кривых изменяется (рис. 12.3, кривые 2, 3, 4). Они показывают, что роль слоев загрузки, расположенных вблизи от поверхности, в осветвлении воды уменьшается. После продолжительной работы фильтра насыщение этих слоев осадком становится предельным и они перестают осветлять воду. На графике (рис. 12.3, кривая 4) отмечена толщина участка загрузки *нас, которая находится в состоянии предельного насыщения к этому времени работы аппарата. По мере насыщения верхних слоев загрузки возрастает роль ниже расположенных, а толщина загрузки, необходимая для извлечения из воды взвеси, увеличивается. Затем наступает такой момент, когда вся толщина загрузки недостаточна для обеспечения необходимой степени осветления воды и концентрация взвеси на выходе из загрузки начинает возрастать (рис. 12.3, кривая 4). Время, в течение которого загрузка способна осветлять воду до требуемой степени, называется временем защитного действия загрузки. До Достижения этого времени на выходе из загрузки получают воду надлежащего качества. По истечении времени защитного Действия качество фильтрата начинает быстро ухудшаться (рис. 12.4).
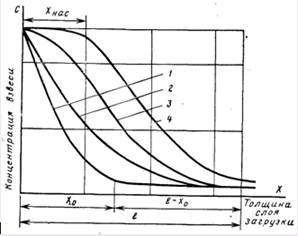
Рис. 12.3. Кинетика осветления воды фильтрованием через зернистую загрузку
Одной из основных задач изучения закономерностей процесса осветления воды фильтрованием является нахождение времени защитного действия загрузки. Выделим в моделе фильтра элементарный слой загрузки толщиной Δх на расстоянии х от ее поверхности (рис. 12.5). К верхнему сечению слоя площадью равной единице, подходит вода с массовой концентрацией частиц С1 а через нижнее сечение она выходит из слоя с концентрацией С2. Уменьшение концентрации частиц в элементарном слое составляет
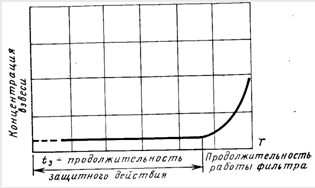
Рис. 12.4. Кинетику осветления воды во времени
Производная дС/дх есть градиент концентрации, т. е. изменение ее на единицу толщины слоя. Градиент концентрации выражен частной производной, так как концентрация частиц в каждом сечении зависит от двух переменных: х — расстояния от поверхности слоя н t —- продолжительности фильтрования. Знак минус в уравнении (12.1) указывает на уменьшение концентрации с увеличением расстояния х от поверхности слоя. Эффект осветления воды рассматриваем как результат двух противоположных явлений — изъятия частиц из воды вследствие их прилипания к зернам загрузки и отрыва ранее прилипших частиц под влиянием гидродинамического воздействия потока. Тогда снижение концентраций частиц на участке Ах может быть выражено равенством
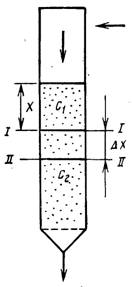
Рис. 12.5. Фильтровальная колонна
где ΔC1 — уменьшение концентрации частиц за счет их прилипания; ΔС2 — увеличение концентрации за счет отрыва частиц.
Снижение концентрации частиц за счет их прилипания может быть принято пропорциональным средней концентрации частиц в объеме выделенного слоя С и оно пропорционально толщине слоя Ад;
(12.3)
где b — параметр фильтрования, определяющий интенсивность прилипания частиц и зависящий от условий фильтрования.
Рост концентрации за счет отрыва ранее прилипших частиц может быть принят пропорционально количеству накопившегося к данному моменту времени осадка р Ах. Кроме того, обратно пропорционален количеству воды, проходящей через слой за единицу времени:
(12.4)
где р — плотность насыщения загрузки осадком, т. е. массовое количество осадка, накопившееся к данному моменту времени в единице объема элементарного слоя загрузки; а — параметр фильтрования, определяющий интенсивность отрыва частиц и зависящий от условий фильтрования; v — скорость фильтрования.
Подставив значения ΔC, ΔС1 и ΔС2 в равенство (12.2), получим
(12.5)
Уравнение (12.5) является основным уравнением, отражающим специфику процесса фильтрования суспензий через зернистую загрузку. В уравнение (12.5) входят две зависимые переменные величины Си ρ, поэтому одного этого уравнения недостаточно для описания процесса.
Вторым, дополняющим его уравнением является уравнение баланса вещества. Через поперечное сечение выделенного слоя с единичной площадью за единицу времени проходит объем воды, равный скорости фильтрования. Следовательно, массовое количество вещества задерживаемого слоем, равно
( 2.6)
Извлекаемые слоем из воды частицы образуют осадок на зернах слоя, накапливающийся в ходе процесса. Количество отложений в слое толщиной Δx; составляет ρ*Δх, а скорость накопления отложений в слое или количество вещества, накапливающегося в нем за единицу времени t, равно
(12.7)
Приравнивая выражения (12.6) и (12.7), получим
'
Дифференциальное уравнение (12.8) является уравнением баланса веществ. Оно показывает, что количество вещества, извлеченного слоем Ах из воды за единицу времени, равно количеству накопившегося в этом слое вещества за тот же промежуток времени.
Дифференцируя уравнение (12.5) по времени и учитывая уравнение баланса (12.8), получим
(12.9)
Это уравнение в дифференциальной форме описывает кинетику процесса осветления при фильтровании суспензий. Аналогично уравнению (12.9) получим дифференциальное уравнение для плотности насыщения
(12.10)
описывающее в дифференциальной форме процесс изменения плотности насыщения фильтрующей загрузки осадком по ее высоте с течением времени. Выражения (12.9) и (12.10) интегрируются, но решение получается в виде бесконечного ряда и его трудно использовать для практических расчетов, которые упрощаются, если воспользоваться критериями подобия для процесса осветления, получаемыми из анализа дифференциального уравнения (12.9). С этой целью преобразуем уравнение (12.9), введя безразмерное отношение мгновенной концентрации к начальной концентрации частиц в воде, поступающей на фильтр: У=С/С0. Тогда
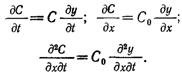
Подставляя эти значения в уравнение (12.9) и сокращая по- сТОянный множитель С0, получим
(12.11)
Введем теперь новые независимые безразмерные переменные
X = bx, Т = at(12.12)
Подставляя эти значения в уравнение (12.11) и сокращая постоянные множители а и b, получим
(12.13)
В уравнение (12.13) в отличие от исходного уравнения (12.9) непосредственно не входят параметры фильтрования а и Ь, которые характеризуют формы протекания процесса. Следовательно, оно является общим для всего многообразия условий протекания процесса фильтрования.
Безразмерные переменные X и Т устанавливают подобие протекания процесса осветления при разных условиях и являются критериями подобия. Изменение концентрации взвеси в воде при ее движении через зернистый слой определяется только значением этих критериев, т. е.
(12.14)
Для процессов, протекающих подобно, масштабные множители обычно определяют методами теории размерностей. Обобщенная кривая С/С0 = f1(Х') при Т' = const, которая дает одновременно представление о влиянии на ход процесса толщины фильтрующего слоя, скорости фильтрования и размера зерен загрузки. Она показывает, что качество фильтрата зависит от перечисленных факторов лишь на определенном участке значений X. При достаточно больших значениях X изменение этих факторов практически не оказывает влияния на качество фильтрата. Поэтому для получения устойчивого эффекта осветления воды фильтровальные аппараты Должны работать в области достаточно больших значений X. При этом условии увеличение скорости фильтрования в определенных пределах не вызовет ухудшения качества фильтрата. Обобщенная кривая С/С0=/2(Т') при X'= const. Как видно из совмещенного графика, необходимый эффект осветления сохраняется на определенном интервале значений Т. Используя теорию размерностей, значения критериев X и Т находим из выражений X' — x/(v7d1'7)
(12.15)
Из уравнения (12.14) можно заключить, что при С/С0 = =const между критериями X и Т должна существовать однозначная зависимость. Экспериментальные данные показывают, что такая зависимость действительно существует и выражается прямой линией
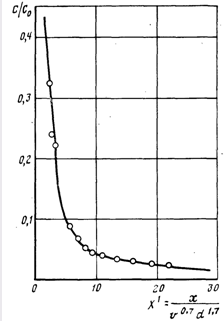
Рис. 12.6. Обобщенный график C/C0=fl(X')
X' = kT' + X'0, Тангенс угла наклона прямой линии k и отрезок, отсекаемый на оси ординат Хо', являются параметрами фильтрования, значения которых при определенном заданном значении С/С0 зависят от физико-химических свойств воды и взвеси. Их определяют экспериментально. Зависимость (12.16) имеет важное практическое значение, так как она устанавливает связь между временем защитного действия загрузки, толщиной ее слоя, размером ее зерен и скоростью фильтрования.
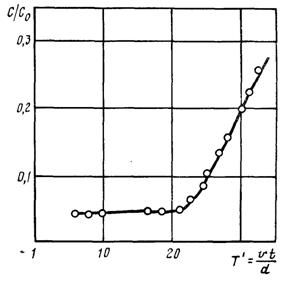
Рис. 12.7. Обобщенный график С/С0=?г(Г)
Подставляя значения X' и Т' из (12.15) в выражение (12.16), получим
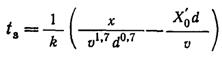Или
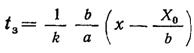
где t3 — продолжительность защитного действия зернистой загрузки; х — толщина слоя загрузки; k и Х0 — константы, значения которых зависят только от требуемого эффекта осветления С/Со (принимаются по номограммам Д. М. Минца); Ъ — параметр, характеризующий интенсивность прилипания; alb — параметр, характеризующий скорость проникновения взвеси в. глубь загрузки.
Из выражения (12.17) следует, что время защитного действия загрузки возрастает с увеличением толщины ее слоя и уменьшается с ростом скорости фильтрования и размера зерен загрузки. Уравнение (12.18) связывает время защитного действия загрузки с параметрами кинетики процесса фильтрования, а/b и b. Опыт свидетельствует, что в неоднородных загрузках фильтровальных аппаратов время защитного действия зависит от эквивалентного диаметра зерен, значение которого и должно учитываться при расчетах по формулам (12.17) и (12.18).
Осадок, образующийся в зернистой загрузке при фильтровании воды, изменяет поперечное сечение и форму поровых каналов, т. е. геометрическую структуру пористой среды. Из теории фильтрования однородных жидкостей известно, что геометрическая структура пористой среды оказывает существенное влияние на ее гидравлическое сопротивление. Поэтому при накоплении осадка гидравлическое сопротивление зернистого слоя изменяется и потери напора в нем растут. Для установления основных закономерностей прироста потери напора необходим учет характера изменения геометрической структуры зернистого слоя при накоплении в нем осадка.
Геометрическую структуру зернистого слоя характеризуют его пористостью и суммарной поверхностью стенок поровых каналов в единице объема слоя. Эти величины входят в выражение для гидравлического уклона. Они изменяются при накоплении осадка в слое. При фильтровании воды через зернистый слой гидравлический уклон (потери напора на единицу длины) равен
где г) — вязкость воды; v — скорость фильтрования; ах — суммарная поверхность стенок поровых каналов в единице объема слоя; п — пористость слоя.
Обозначим гидравлический уклон, поверхность поровых каналов и пористость слоя в начальный момент фильтрования через t0; а0 и по, а в момент времени t — i, а, пи подставим в выражение (12.19), получим
Сопоставляя отношение (12.19) и (12.20), получим
По мере заиления загрузки ее пористость уменьшается. Что же касается характеристики поверхности поровых каналов, омываемой потоком, то здесь наблюдаются две противоположные тенденции. С одной стороны, зерна фильтрующего слоя постепенно обрастают адсорбированными частицами взвеси и укрупняются в объеме, что приводит к увеличению поверхности, омываемой потоком.
С другой стороны, отложения на каждом зерне, разрастаясь, соединяются между собой. На отдельных участках порового пространства, в которых ранее происходило движение воды, образуется "мертвая зона", где движение воды отсутствует. Это приводит к уменьшению поверхности, омываемой потоком жидкости. В среднем отношение может быть принято равным единице.
Тогда допустимо в первом приближении пренебречь изменением поверхности и выражение (12.21) трансформировать в
Обозначим объем осадка, накопившегося в единице объема загрузки, через Ап (удельный объем осадка). Учитывая, что
п = п0-Δп,(12.23)
формулу (12.22) можно переписать в виде
или
где V=Δn/n0 — объем осевшей массы частиц в единице объема порового пространства.
Обозначив массовую концентрацию частиц в единице объема осадка через у, получим
(12.26)
где ρ— плотность насыщения (массовое количество осадка в единице объема зернистого слоя).
Потеря напора в слое однородной зернистой загрузки при фильтровании суспензии
(12.27)
где L — толщина слоя.
Подставляя в (12.27) значение i по формуле (12.24) и Ал по формуле (12.26), получим
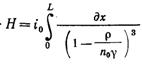
Непосредственное использование выражения (12.28) затруднительно, так как плотность насыщения ρ изменяется не только по высоте слоя, но и во времени согласно уравнению (12.10). Решение уравнения (12.10) показывает, что отношение плотности насыщения в любой момент времени и в любом сечении загрузки к предельной плотности насыщения зависит только от значений безразмерных критериев (12.12), т. е.
(12.29)
Заменяя ρ в формулах (12.25) и (12.28) его значениями из формулы (12.29), получим
(12.30)
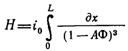(12.31)
(12.32)
Величина А является самостоятельной физической характеристикой процесса фильтрования и представляет собой предельно возможную в данных условиях насыщенность порового пространства отложениями или отношение предельного удельного объема осадка к начальной пористости чистой загрузки. Выражение (12.30) указывает на связь между предельной наторая находится в состоянии предельного насыщения, при этом ф = 1 и
(12.33)
Из (12.33) следует, чем больше предельная насыщенность, тем больше предельный гидравлический уклон, а следовательно, и гидродинамические силы, которые воздействуют на структуру осадка. Следовательно, предельный гидравлический уклон и предельная насыщенность характеризуют прочность осадка.
Потеря напора в слое фильтрующей загрузки толщиной х в момент времени t может быть определена с использованием интеграла (12.31) и заменой его суммой
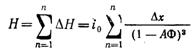
Прирост потери напора равен разности между потерей напора в заиленной загрузке и начальной потерей в чистой загрузке, а, именно:
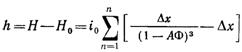(12.35)
Потеря напора в любом фильтрующем слое и ее прирост зависит от толщины слоя. Однако, при достаточно большой толщине слоя прирост потери напора будет определяться только распределением осадка по толщине слоя во времени. Такой слой работает в автомодельной области. Рассмотрим закономерности изменения потери напора в слоях, работающих в автомодельной области. Умножив левую и правую части равенств (12.35) на параметр b и разделив на i0, получим
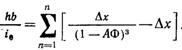(12.36)
Суммирование производим по интервалам значений Δх, причем для каждого интервала принимаем среднее значение функции Ф, которая представляет собой отношение среднего для Данного интервала значения плотности насыщения к предельной плотности насыщения. При соблюдении условия автомодельности комплекс h b/i0 не зависит от критерия X, а только от распределения осадка по интервалам значений х и от критерия Т, с изменением которого меняется распределение осадка. Поэтому в автомодельной области
(12.37)
Следовательно, безразмерный комплекс h b/i0 является новым критерием подобия процесса фильтрования. Он представляет собой обобщенную потерю напора, так же как критерий X — обобщенную толщину фильтрующего слоя, а критерий Т — обобщенную продолжительность фильтрования. Если известна величина h*b/i0 при определенных значениях потери напора, параметра b и начального гидравлического уклона i0, то простым пересчетом можно определить потерю напора при других значениях b и 10, при сохранении условия
(12.38)
При различных условиях проведения процесса фильтрования свойства примесей, скорость фильтрования, крупность зерен загрузки будут разными. Поэтому различным будет и прирост потери напора за определенный промежуток времени, однако равным значениям Т и А отвечают равные значения комплекса h*b/i0.
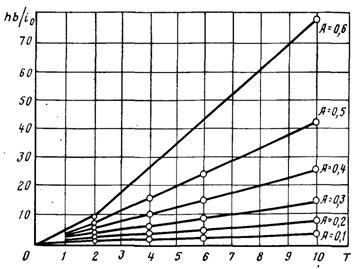
Рис. 12.8. Обобщенный график роста потери напора
Это свидетельствует о возможности построения графика зависимости h-b/i0 от критерия Т и параметра А, который может быть использован для определения потери напора в любом рассматриваемом случае. Подобный график (рис. 12.8) построен на основании расчетов по формуле (12.35) с использованием уравнения (12.10). График позволяет определить прирост потери напора в фильтре в любой момент времени, если известны параметры процесса фильтрования a, b и А, а также гидравлический уклон t0. Обобщенный график (рис. 12.8) воспроизводит характер изменения потери напора.
Для упрощения расчетов можно с достаточной степенью точности предположить, что с самого начала процесса темп прироста потери напора не меняется, т. е.
(12.39)
где F(A) — тангенс угла наклона прямолинейного участка графика (рис. 12.9) зависящий только от величины предельной насыщенности.
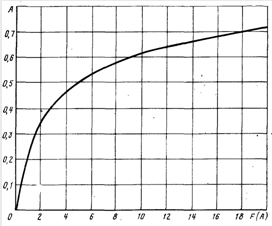
Рис. 12.9. Значения функции F(Л)
Подставляя значение Т = а*t в уравнение (12.39), получаем формулу для расчета темпа прироста потери напора
(12.40)
При линейном приросте потери напора в процессе фильтрования его продолжительность до момента достижения предельной потери напора tH равна
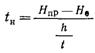
где Япр — предельно допустимая потеря напора в загрузке фильтра, определяемая высотной схемой сооружений. С учетом зависимости (12.40) имеем
Уравнения (21.41) и (12.42) применимы только к однородным по размеру зерен загрузкам.
Но в реальных фильтрах мы имеем дело с неоднородными загрузками, фракции которых хотя и перемешаны друг с другом, но так, что средний диаметр зерен каждого горизонтального слоя постепенно увеличивается от слоя к слою в направлении от поверхности загрузки к ее основанию в результате гидравлической сортировки зерен при промывке в восходящем потоке воды. Так как потеря напора возрастает в основном в первых по направлению движения воды слоях загрузки, то все величины в правой части уравнения (12.40) должны быть отнесены к диаметру зерен загрузки, при которой вычисленный прирост потери напора для однородной загрузки будет равен потери напора для данной неоднородной загрузки. Для этого используют предложение В. П. Криштула, согласно которому потеря напора в неоднородной загрузке с эквивалентным диаметром dэ равна потере напора в однородной загрузке с таким же диаметром, помноженной на квадрат коэффициента неоднородности. Последний определяется отношением эквивалентного диаметра к среднему диаметру зерен первого по движению воды слоя загрузки с толщиной, равной 20% полной высоты загрузки d20. Таким образом,
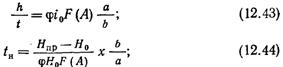
Где
(12.45)
Следует отметить, что отношение d3/d20 зависит не только от зернового состава загрузки, но и от направления движения обрабатываемой воды. Оно будет больше единицы при движении. воды сверху вниз, как в обычных скорых фильтрах, и меньше единицы при движении снизу вверх, как в контактных осветлителях и фильтрах системы АКХ; в уравнениях (12.43) и (12.44), как и в уравнениях для определения времени защитного действия (12.18), все параметры фильтрования относятся к эквивалентному диаметру зерен неоднородной загрузки.
Оптимизация режима фильтрования. Расчет загрузки скорых фильтров
Из изложенного следует, что процесс обработки воды фильтрованием через зернистую загрузку описывается двумя основными уравнениями, определяющими время защитного действия загрузки (12.18) и время, в течение которого достигается предельная потеря напора (12.44). Эти уравнения относятся к автомодельной области работы фильтров, в которой изменение скорости фильтрования, толщины слоя загрузки и размера зерен не влияют или влияют незначительно на концентрацию взвеси в фильтрате. Соотношение между продолжительностью защитного действия загрузки и времени, в течение которого достигается предельная потеря напора, могут быть различные. Когда t3>tH фильтр выключают на промывку в связи с тем, что дальнейший прирост потери напора невозможен, так как существующий напор, обусловленный расположением сооружений, расходуется на преодоление сопротивления загрузки. Когда t3
Анализ уравнений (12.18) и (12.44) показывает, что путем изменения толщины слоя или эквивалентного диаметра зерен загрузки при одновременном увеличении скорости фильтрования всегда можно уменьшить t3, если t3>tH, или t„, если tH> >t3, и добиться, таким образом, равенства t3 = tн, при котором обеспечивается максимальная производительность фильтровального аппарата. Тем не менее с точки зрения санитарной надежности целесообразно принимать значение t3/tn>1, так как при этом в течение всего фильтроцикла гарантируется высокое качество фильтрата, повышается степень санитарной надежности сооружений. Чем больше отношение t3/tH, тем выше степень санитарной надежности фильтров, но тем они дороже в строительстве и эксплуатации, так как с увеличением этого отношения растет неиспользуемый скрытый резерв производительности фильтров. Поэтому основная идея расчета фильтрующих загрузок состоит в том, что исходят из определенного, заранее заданного отношения продолжительности защитного действия загрузки к времени, в течение которого достигается потеря напора (t/tn= 1,2 ... 1,3), обеспечивающего вместе с тем достаточную санитарную надежность и экономичность работы фильтров. Режим работы фильтровального аппарата, при котором обеспечивается указанное соотношение, может быть назван оптимальным.
Задача определения расчетной скорости фильтрования и параметров загрузки фильтров при оптимальном режиме их работы сводится к совместному решению уравнений (12.18) и (12.44), в которых заданными величинами являются параметры фильтрования a/b, b и А (определяются по результатам технологического анализа воды): продолжительность рабочего цикла (в соответствии с требованиями СНиП 2.04.02—84 расчетная продолжительность фильтроцикла принимается 12 ч); продолжительность защитного действия загрузки t3 назначается в соответствии с принятым для оптимального режима отношением t3/tu. Предельная потеря напора Нпр назначается в соответствии с высотной схемой водоочистного комплекса. Неизвестными величинами в уравнениях (12.18) и (12.44) остаются скорость фильтрования v, толщина слоя загрузки х, эквивалентный диаметр зерен йэ и степень неоднородности загрузки ср. Последние две величины взаимосвязаны, так как зависят от зернового состава фильтрующей загрузки. Эквивалентный диаметр d3 вычисляют. Параметр ф находят по экспериментальному графику (рис. 12.10) по величине отношения d20/d3. Таким образом, имеем три неизвестных при двух уравнениях: скорость фильтрования, толщину слоя фильтрующей загрузки и ее зерновой состав. Поэтому задача расчета фильтров на оптимальный режим их работы имеет несколько решений. Следовательно, для получения одного определенного решения необходимо задаться или скоростью фильтрования, или толщиной слоя загрузки, или ее зерновым составом. Задавшись, например, зерновым составом фильтрующей загрузки, расчетом определяют ее необходимую толщину и скорость фильтрования. Для расчетов удобно преобразовать уравнение (12.44), решив его относительно толщины слоя х. Тогда оно примет вид
(12.46)
Преобразуем также уравнение (12.17), представив его в виде
(12.47)
фильтрование вода зернистый напор
где 
) — критериальный комплекс.
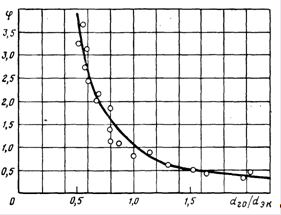
Рис. 12.10. График зависимости 
Значен