Доверительный интервал. Проверка статистических гипотез

Доверительный интервал.

Проверка статистических гипотез

1. Доверительный интервал

Точечные оценки являются приближенными, так как они указывают точку на числовой оси, в которой должно находиться значение неизвестного параметра. Однако оценка является приближенным значением параметра генеральной совокупности, которая при разных выборках одного и того же объема будет принимать разные значения, поэтому в ряде задач требуется найти не только подходящее значение параметра а, но и определить его точность и надежность.

Для этого в математической статистике используется два понятия – доверительный интервал и доверительная вероятность. Пусть для параметра а из опытных данных получена несмещенная оценка  Требуется определить возможную при этом величину ошибки и вероятность того, что оценка не выскочит за пределы этой ошибки (надежность).

Зададимся некоторой вероятностью b (например, b = 0,99) и найдем такое значение e > 0, для которого

Представим это выражение в виде

Это значит, что с вероятностью b точное значение параметра а находится в интервале  l_e

                                                                                l_e

Здесь параметр а – неслучайная величина, а интервал  l_e  является случайным, так как  - случайная величина.  Поэтому вероятность b лучше толковать, как вероятность того, что случайный интервал l_e накроет точку а. Интервал l_eназывают доверительным интервалом, а вероятность b - доверительной вероятностью (надежностью).

Пример.  Если при измерении какой-то величины Х указывается абсолютная погрешность Dх, то это, по существу, означает, что погрешность измерения, являясь случайной величиной, равномерно распределена в интервале (-Dх, Dх) и  где Х* - измеренная величина, а х – ее точное значение.  Здесь b = 1, e = Dх и  l_e = (x*- Dх, x* + Dх).

1.1 Доверительный интервал для математического ожидания

В качестве еще одного примера рассмотрим задачу о доверительном интервале  для математического ожидания.  Пусть проведено n независимых опытов измерения случайной величины Х с неизвестным математическим ожиданием m_x и дисперсией s².  На основании опытных данных Х₁, Х₂, ... , Х_n построим выборочные оценки

Требуется построить (найти) доверительный интервал l_e, соответствующий доверительной вероятности b, для среднего генерального m_x.

Так как среднее выборочное  представляет сумму n независимых одинаково распределенных случайных величин  то при достаточно большом  объеме выборки согласно центральной предельной теоремы ее закон близок к нормальному.  Существует эмпирическое правило, по которому при объеме выборки   n ³ 30 выборочное распределение можем считать нормальным.

Ранее было показано, что   Найдем теперь такую величину e(b) > 0,  для которой выполняется равенство

Считая случайную величину  нормально распределенной, имеем

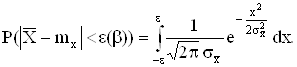
После замены    имеем

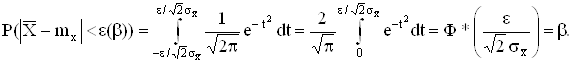
По табличным значениям функции Лапласа Ф*(z) находим аргумент, при котором она равна b.  Если этот аргумент обозначить Z_b, то тогда

Среднее квадратичное значение  приближенно можно заменить

  где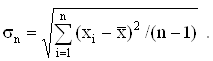 

Таким образом, доверительный интервал для среднего генерального равен:

l_e =

Если пользоваться табличными значениями интеграла вероятностей

то доверительный интервал принимает вид

l_e =

1.2 Распределение Стьюдента

При малом объеме выборки (n < 30) полученный доверительный интервал для среднего генерального, использующий нормальное распределение случайной величины , может быть очень грубым.

Для более точного получения доверительного интервала необходимо знать закон распределения случайной величины  при малом объеме выборки.  Для этого воспользуемся следующим результатом.  Пусть Х₁, Х₂, ... , Х_n – выборка нормально распределенной случайной величины Х, тогда, как доказано, случайная величина

подчиняется распределению Стьюдента c  n – 1 степенью свободы, плотность распределения которого имеет вид

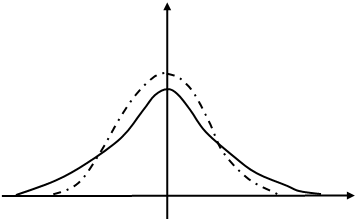
где  - гамма функция.  Эта плотность, как видно из формулы, зависит только от числа опытов n.  Ниже представлены графики плотностей нормированной (m_x = 0,  s = 1) нормально распределенной и с распределением Стьюдента (n = 4) случайных величин.