Адгезионное взаимодействие наночастиц
Недавно выяснилось, что в основе механизма повышенной адгезии наночастиц лежат силы молекулярного взаимодействия, т.е. силы Ван-дер-Ваальса. Независимо от гидрофобности поверхности силы Ван-дер-Ваальса перевешивают капиллярные силы и создают прочность сцепления 10Н/см2. Теоретически массивы многостенных углеродных нанотрубок (МСНТ) диаметром 20-30нм и плотностью ~ 1011-1012 нанотрубок/см2 могли бы обеспечить адгезию более 500Н/см2.
Адгезия - это самопроизвольное поверхностное явление, которое приводит к снижению поверхностной энергии. Адгезия и смачивание жидкости относятся к одному из видов адгезионного взаимодействия. Его особенности определяются как свойствами твердой поверхности так и свойствами жидкости. Адгезией (сцеплением, притяжением или прилипанием) называют связь между разнородными конденсированными телами при их молекулярном контакте. К конденсированным телам относятся жидкие и твердые тела. При адгезии сохраняется граница раздела фаз, образованная двумя твердыми телами, твердым телом и жидкостью, т.е. граница раздела т-т и ж-т. Возможна адгезия двух разнородных жидкостей на границе раздела ж-ж.
Самопроизвольно идут процессы, связанные с уменьшением поверхностной энергии, в данном случае энергии Гиббса.
∆ Gs < 0
В результате адгезии удельная свободная поверхностная энергия уменьшается на величину, которая характеризует работу адгезии Wа.
Существуют различные модели адгезии наночастиц.
Так, по теории Джонсона-Кендела-Робертса, сила F притяжения (адгезии) шарообразной частицы одной фазы и бесконечной по протяженности плоской поверхностью другой или той же фазы выражается формулой:
![]() ,
,
где А – константа Гамакера для данной системы (константа дисперсионного взаимодействия молекул фаз), r – радиус частицы, h – расстояние между поверхностью сферической частицы и плоской поверхностью.
Модель Маугиса (1992) является наиболее сложным и точным подходом. Его можно использовать для любых систем (любых материалов): как с большой, так и с малой адгезией. Степень адгезии определяется параметром λ:
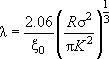
где ξ0 – межатомное расстояние.
Адсорбционный монослой ПАВ. Локальная концентрация и образование островковой наноразмерной структуры
адгезионный наночастица лиофобная
Для управлением массопереносом жидкостей различной природы в микро- и наноканалах в ряде случаев приходится модифицировать внутреннюю поверхность каналов нанесением монослоев поверхностно-активных веществ (ПАВ). Простейшая технология такого нанесения предполагает пропитку каналов раствором ПАВ, адсорбцию на стенки канала из растворов в течение некоторого времени, удаление раствора и просушку каналов. При этом объемная концентрация ПАВ в растворе стандартизуется и используется для обработки каналов с широким диапазоном радиусов.
Хорошо известно, что свойства тонкой пленки отличаются от свойств массивного материала, особенно если толщина пленки очень мала. Эта «особенность» определяется спецификой структуры пленки, которая в свою очередь, обусловлена процессами образования тонкой пленки. Существует большое количество методов и процессов получения тонких пленок (от прокатки до осаждения материала на подложку атом за атомом). Чаще всего тонкие пленки получают методами осаждения.
Образование тонких пленок в вакууме происходит в несколько этапов. Укрупнено можно выделить следующие этапы образования пленки:
- образование зародышей;
- рост зародышей, образование островков;
- коалесценция островков;
- образование каналов;
- рост сплошной пленки.
Для современной науки (разделы электроники: микро - и наноэлектроника) и техники большой интерес представляют островковые пленки, то есть пленки, формирование которых завершили на этапе образования островков. Уникальные свойства (электронные, оптоэлектронные и др.) островковых пленок связаны с тем, что их размеры во всех трёх измерениях лежат в нанометровом диапазоне. Этот факт обусловливает эффект размерного квантования энергетических уровней электрона, находящегося внутри островковой наноструктуры (островка). Поведение электрона внутри наноразмерного островка подобно его поведению внутри трёхмерной потенциальной ямы. По этой причине островковые пленки или островковые наноструктуры (ОНС) диаметром от 2 до 10 нм получили название «квантовые точки».
Атомистическая теория роста пленок, авторами которой являются Уолтер и Родин, описывает процесс зародышеобразования с помощью методов статической физики и позволяет представить этот процесс с помощью зародышей малого размера, состоящих из небольшого числа отдельных атомов. Стабильные зародыши называются зародышами закритического размера, а нестабильные - докритического размера.
После образования зародышей закритического размера на подложке начинается рост пленки, в результате которого адсорбируемые атомы и зародыши докритического размера мигрируют на поверхности, захватываясь закритическими зародышами (островками).
Островки разрастаются, просвет между ними уменьшается. В этот момент пленка представляет собой совокупность островков закритического размера, пока не связанных между собой гальванически. Такую пленку называют островковой, состоящей из островков или квантовых точек. В зависимости от расстояния между островками преобладают различные механизмы электропроводимости. При сравнительно больших расстояниях (10 нм) - термоэлектронный механизм, а при малых зазорах (2,5 нм) - туннельный эффект переноса носителей.
Молекулярно-лучевая эпитаксия (МЛЭ) - один из современных и перспективных технологических методов выращивания монокристаллических слоев и полупроводниковых структур на их основе. МЛЭ представляет собой процесс эпитаксиального роста тонких слоев различных соединений (рис. 1) за счет реакций между термически создаваемыми молекулярными или атомными пучками соответствующих компонентов и поверхностью подложки, находящейся в сверхвысоком вакууме при повышенной температуре.
В сверхвысоком вакууме создаются молекулярные пучки с помощью эффузионнных ячеек, температура которых тщательно контролируется, как правило, с помощью ЭВМ. Выбирая должным образом температуры подложки и ячеек, получают эпитаксиальные пленки требуемого химического состава. С помощью заслонок можно быстро изменять потоки различных веществ, создавая резкие профили состава и легирования. Однородность состава пленки и ее кристаллическая структура определяется однородностью молекулярных пучков по площади подложки материалов.
Преимущество метода МЛЭ состоит в высокой точности задания концентрации легирующих примесей. Кроме того, данный метод позволяет размещать в оборудовании для МЛЭ приборы, дающие возможность анализировать параметры слоев непосредственно в процессе выращивания.
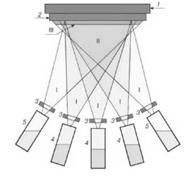
Рис. 1. Схема установки МЛЭ: I - зона генерации молекулярных пучков; II -зона смешивания испаряемых элементов; III - зона кристаллизации на подложке; 1 - блок нагрева; 2 - подложка; 3 - заслонка отдельной ячейки; 4 - эффузионнные ячейки основных компонентов пленки; 5 - эффузионнные ячейки легирующих примесей.
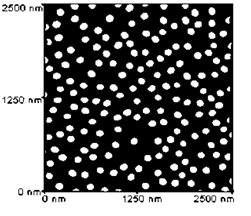
Рис. 2. Однородные островки Ge/Si.
Влияние ПАВ на поверхностные силы и устойчивость лиофобных наносистем
Под устойчивостью дисперсной системы понимают постоянство во времени ее состояния и основных свойств: дисперсности, равномерного распределения частиц дисперсной фазы в объеме дисперсионной среды и характера взаимодействия между частицами. Дисперсные системы с жидкой дисперсионной средой по характеру взаимодействия фаз подразделяются на лиофильные. В лиофобных системах сольватация поверхности частичек растворителем слабая и не может скомпенсировать избыточную поверхностную энергию. Поэтому частички дисперсной фазы могут слипаться друг с другом в более крупные агрегаты. Этот процесс называется коагуляцией, от латинского coagulatio – свертывание, сгущение. При этом удельная площадь поверхности, а вместе с ней и избыточная свободная поверхностная энергия снижается. Примерами гидрофобных дисперсных систем являются пены, эмульсии типа "масло в воде", латексы, суспензии, золи металлов, сульфидов, галогенидов, оксидов и гидроксидов, а также золи неметаллов (Au, Ag, ZnS, As2S3, AgI, SiO2, TiO2, Al(OH)3, Fe(OH)3, S, Se и другие). Если дисперсная фаза состоит из капелек жидкости, то процесс их слияния называется коалесценцией.
Н. П. Песков (1920) ввел понятие о двух видах устойчивости дисперсных систем: седиментационной (кинетической) и агрегативной. Седиментационная устойчивость позволяет системе сохранять равномерное распределение частиц в объеме, то есть противостоять действию силы тяжести и процессам оседания или всплывания частиц. Основными условиями этой устойчивости являются высокая дисперсность и участие частиц дисперсной фазы в броуновском движении. Агрегативная устойчивость – это устойчивость по отношению к слипанию частичек коллоидной системы в более крупные агрегаты. Иногда в качестве отдельного вида выделяют устойчивость дисперсной системы по отношению к расслоению фаз – фазовую устойчивость. Расслоению может предшествовать коацервация (coacervatio – накопление), то есть выделение в растворе капель, обогащенных растворенным веществом. Дальнейшее слияние этих капель ведет к разделению жидкости на две макрофазы: коацерват – фазу, которая обогащена растворенным веществом, и жидкость, находящуюся с ней в равновесии. Это явление особенно характерно для растворов высокомолекулярных соединений.
По теории Пескова, устойчивость коллоида объясняется присутствием кроме дисперсной фазы и дисперсионной среды третьего вещества – стабилизатора, образующего вокруг коллоидной частицы сольватный слой. Этот процесс – лиофилизация коллоида. Этот процесс можно вызвать адсорбцией поверхностно-активных веществ на поверхности коллоидной частицы.
Поверхностно-активные вещества (ПАВ) - химические соединения, которые, концентрируясь на поверхности раздела фаз, вызывают снижение поверхностного натяжения. Основной количественной характеристикой ПАВ является поверхностная активность - способность вещества снижать поверхностное натяжение на границе раздела фаз.
Классификация методов определения размеров наночастиц. Принцип работы сканируемых зондовых приборов
1) Электронная микроскопия. Электронный микроскоп (ЭМ, electron microscope) - высоковольтный вакуумный прибор, в котором увеличенное изображение объекта получают с помощью потока электронов. Разрешающая способность электронного микроскопа достигает 0,1 нм.
Основными типами электронных микроскопов являются сканирующий (растровый) и трансмиссивный (просвечивающий).
2) Растровая электронная микроскопия. Растровый электронный микроскоп (РЭМ, SEM) — прибор, позволяющий получать изображения поверхности образца с большим разрешением. Растровый электронный микроскоп основан на использовании предварительно сформированного тонкого электронного луча, положением которого управляют с помощью электромагнитных полей. Электронный зонд последовательно проходит по поверхности исследуемого образца. Регистрация электронов, выходящих из объекта, а также других видов излучения (характеристического, светового) дает информацию о различных свойствах микроучастков изучаемого объекта. Соответственно этому системы индикации и другие элементы растровых микроскопов различаются в зависимости от вида регистрируемого излучения.
3) Просвечивающая электронная микроскопия. Просвечивающий электронный микроскоп (ПЭМ, TEM) – установка, в которой изображение от ультратонкого объекта (толщиной порядка 0,1 мкм) формируется в результате взаимодействия пучка электронов с веществом образца с последующим увеличением магнитными линзами (объектив) и регистрацией на флуоресцентном экране.
4) Рентгеновская дифрактометрия. Рентгеновский дифрактометр (SAXS) – прибор для измерения интенсивности и направления рентгеновских пучков, дифрагированных на исследуемом образце. Прибор применяется для решения различных задач рентгеновского структурного анализа, рентгенографии материалов, исследования реальной структуры монокристаллов. Он позволяет измерять интенсивность дифрагированного в заданном направлении излучения с точностью до десятых долей % и угол дифракции с точностью от нескольких минут до долей секунды.
5) Сканирующая зондовая микроскопия. Сканирующий зондовый микроскоп (СЗМ, SPM) – прибор, в котором исследование микрорельефа поверхности и ее локальных свойств проводится с помощью специальным образом приготовленных зондов в виде игл. Рабочая часть таких зондов (острие) имеет размеры порядка десяти нанометров. Характерное расстояние между зондом и поверхностью образцов в зондовых микроскопах по порядку величин составляет 0.1 – 10 нм.
В основе работы зондовых микроскопов лежат различные типы взаимодействия зонда с поверхностью. В самом простом случае острие зонда находится в непосредственном соприкосновении с исследуемой поверхностью. Зондовый датчик движется вдоль поверхности, при этом регистрируется изменение изгиба кантилевера или других величин, пропорциональных взаимодействию зонда и исследуемого образца. Кроме простого сканирования, при котором получается карта распределения величины, существуют и другие методики применения СЗМ. Например, при спектроскопии получают множество зависимостей одной величины от другой в различных точках поверхности. При литографии путем воздействия на образец на его поверхности воссоздается заранее заданный рисунок, например, электрической наносхемы. При наноманипуляциях с помощью зонда можно разрезать живую клетку или передвинуть большую молекулу углеродной нанотрубки на заранее подготовленные контакты, получив нанодиод.
Задачи1. В образце синтезированных наночастиц золота диаметр частиц распределен приблизительно нормально, со средним арифметическим`х и со средним квадратичным отклонением s, указанным в таблице ниже, для соответствующего номера задачи. Вычислить (для своего номера задачи) долю частиц в образце, диаметры которых находятся в пределах от x1 до x2, приняв m =`х и s = s.
| № задачи | `х /нм | s/нм | x1/нм | x2/нм |
| 10 | 7.1 | 2.4 | 5.0 | 10.0 |
Решение
Вычислим аргументы z1 и z2 стандартной функции Гаусса, приняв m =`х = 7,1 нм и s = s = 2,4 нм:
z1 = (x1 – m)/s = (5,0 нм – 7,1 нм)/(2,4 нм) = -0,875;
z2 = (x2 – m)/s = (10,0 нм – 7,1 нм)/(2,4 нм) = 1,208;
По таблицам интегральной функции Лапласа найдем F(-0,875) =-Ф(0,875) =.F(1,208) = .
Искомая доля частиц:
F(1,208) - F(-0,875) =
Ответ: 1) 8,61 нм; 2) 0,77 нм; 3) 6,9%.
2. Вычислить силу адгезии наночастицы жидкости к плоской поверхности твёрдого материла, зная константу Гамакера А двух данных фаз, радиус частицы r и величину зазора h между частицей и поверхностью, указанные в следующей таблице (для своего номера задачи):
| № задачи: | 23 | 24 | 25 | 26 | 27 |
A·1021/Дж | 45 | 46 | 47 | 48 | 49 |
| r/нм | 15 | 13 | 11 | 9 | 7 |
| h/нм | 0,172 | 0,171 | 0,170 | 0,169 | 0,168 |
Решение
По теории Дронсона-Кендела-Робертса, сила F притяжения (адгезии) шарообразной частицы одной фазы и бесконечной по протяженности плоской поверхностью другой или той же фазы выражается формулой
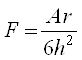 ,
,
где А – константа Гамакера для данной системы (константа дисперсионного взаимодействия молекул фаз), r – радиус частицы, h – расстояние между поверхностью сферической частицы и плоской поверхностью.
Имеем:
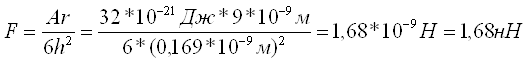
Ответ: 1,68 нН
3. Рассчитать потенциальную энергию u взаимодействия двух плоскопараллельных пластин, находящихся в водном растворе электролита с концентрацией с, при значении потенциала диффузного слоя φs, относительной диэлектрической проницаемости εr и температуре t. При расчете принять константу Гамакера А* = 3.0·10–20 Дж. Вычисления сделать для расстояний между пластинами h: 2, 5, 10, 15, 25, 50 нм. Построить график зависимости u = f(h).
| Задача | Электролит | c,ммоль/л | t, °С | εr | φd, мВ |
| 42 | KBr | 1,5 | 23 | 79,1 | 18 |
Решение
Потенциальная энергия взаимодействия двух бесконечно больших плоских пластин (в расчете на единицу площади):
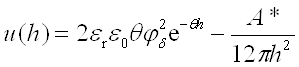 .
.
Первый член отвечает энергии электростатического отталкивания, второй член – энергии притяжения из-за дисперсионных (межмолекулярных) взаимодействий.
A* – константа Гамакера, h – расстояние между поверхностями пластин, er – относительная диэлектрическая проницаемость среды между пластинами, e0 – электрическая постоянная (диэлектрическая проницаемость вакуума), p – число пи, jd – потенциал на границе диффузной части и плотной части двойного электрического слоя, величина θ (параметр Дебая) равна обратной величине толщины диффузного слоя d:
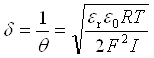 ,
, ![]() – ионная сила раствора,
– ионная сила раствора,
F – постоянная Фарадея.
Рассчитаем ионную сила раствора 1,5 ммоль/л раствора KBr:
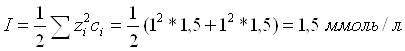
Рассчитаем величину толщины диффузного слоя d:
![]()
Параметр Дебая:
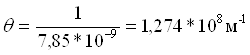
Потенциальная энергия взаимодействия двух бесконечно больших плоских пластин (в расчете на единицу площади):
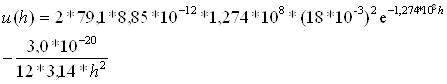 .
.
Результаты расчета энергии (Дж/м2)
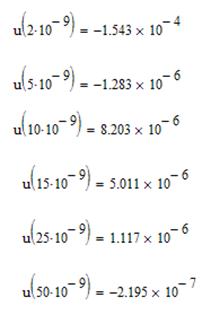
Строим график зависимости в программе MathCad.
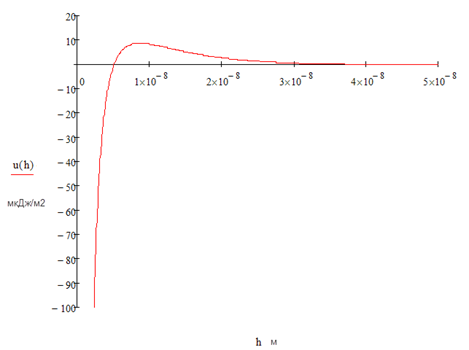
4. Частицы аэросила SiO2 в водной среде при рН = 6,2 имеют дзета-потенциал – 30,7 мВ. На какое расстояние и к какому электроду сместятся частицы за 30 минут, если напряжение при электрофорезе 110 В, расстояние между электродами 25 см, относительная диэлектрическая проницаемость дисперсионной среды 80,16, вязкость среды 1.002 мПа с?
Решение
Скорость течения (линейная скорость электроосмоса) при заданной напряженности поля E:
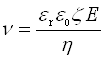 .
.
где er – относительная диэлектрическая проницаемость среды, e0 – электрическая постоянная (диэлектрическая проницаемость вакуума), η – вязкость среды, ζ – электрокинетический потенциал.
Напряженность поля:
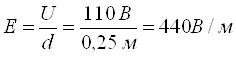
Скорость течения:
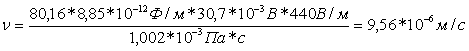
За 30 минут частицы сместятся на расстояние:
![]()
Так как частицы заряжены отрицательно, то они будут двигаться к аноду.
Ответ: 17 мм.
5. Средний квадратичный сдвиг наночастиц золя платины в воде за время 1 с составляет 3,5 мкм. Определить объем наночастицы, если вязкость среды 1,09·10–3 Па·с при 17 °C. Принять сферическую форму частиц.
Решение
Зависимость для среднего квадратичного сдвига (хскв):
![]()
Отсюда коэффициент диффузии:
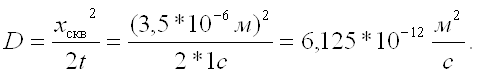
Из уравнения Эйнштейна радиус частицы:
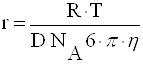
где NА – число Авогадро, 6 · 10 23 молекул/моль;
h – вязкость дисперсионной среды, Н · с/м2 (Па · с);
r – радиус частицы, м;
R – универсальная газовая постоянная, 8,314 Дж/моль · К;
T – абсолютная температура, К.
Имеем:
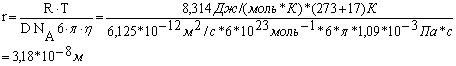
Находим объем частицы:
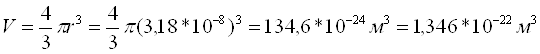
Ответ: 1,346*10-22 м3.
Список использованной литературы
ДерягинБ. В., Чураев Н. В., МуллерВ. М., Поверхностные силы, М., 1985; Дерягин Б. В., Теория устойчивости коллоидов и тонких пленок, М., 1986. Я И Рабинович
История химии под ред. Менделеева. Классическое издание о развитии химической науки - репринт 1899 г. BIBLIARD
Подобные работы: