Расчет зеркальной параболической антенны с облучателем в виде конического рупора
1. РАСЧЕТ ГЕОМЕТРИЧЕСКИХ И ЭЛЕКТРОДИНАМИЧЕСКИХ ПАРАМЕТРОВ ОБЛУЧАТЕЛЯ И ПАРАБОЛОИДА
1.1 Выбор фидера. Определение шумовой температуры фидерного тракта
1.2 Определение диаметра раскрыва
1.3 Аппроксимация аналитического вида ДН облучателя функцией вида cosn/2Y
1.4 Определение угла раскрыва и фокусного расстояния зеркальной антенны
2. РАСЧЕТ ГЕОМЕТРИЧЕСКИХ И ЭЛЕКТРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ПОЛЯ
2.1 Диаграммы направленности облучателя
2.1 Распределение поля в апертуре зеркала
3. РАСЧЕТ ПРОСТРАНСТВЕННОЙ ДИАГРАММЫ НАПРАВЛЕННОСТИ И ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПАРАБОЛИЧЕСКОЙ АНТЕННЫ
4 КОНСТРУКТИВНЫЙ РАСЧЕТ АНТЕННЫ
4.1 Расчет профиля зеркала
4.2 Выбор конструкции зеркала
4.3 Определение допусков на точность изготовления
5. СОПОСТАВЛЕНИЕ РАСЧЕТНОГО И ЗАДАННОГО УРОВНЯ БОКОВЫХ ЛЕПЕСТКОВ, ВЫРАБОТКА РЕКОМЕНДАЦИИ ДЛЯ ОБЕСПЕЧЕНИЯ СООТВЕТСТВИЯ ЭТИХ УРОВНЕЙ
ЗАКЛЮЧЕНИЕ
СПИСОК ЛИТЕРАТУРЫ
ИСХОДНЫЕ ДАННЫЕ
Рассчитать малошумящую параболическую антенну. Исходные данные:
Частота сигнала генератора, подводимого к антенне, f = 1,0 ГГц;
Ширина главного лепестка ДН на уровне половинной мощности 2Q0.5
2QН0.5 = 49 мрад;
2QЕ0.5 = 54 мрад;
Уровень боковых лепестков (- 17) дБ;
Тип облучателя: Полуволновой вибратор с дисковым контррефлектором;
Средняя яркостная температура неба Тнср = 5 К;
Температура шумов приемника Тпр = 1800 К;
Длина фидерной линии lф=5 м.
Параболические антенны в последнее время находят все более широкое применение в космических и радиорелейных линиях связи. В 1888 году известный немецкий физик Г. Герц в своих опытах по СВЧ оптике впервые применил в качестве фокусирующего устройства параболический цилиндр. Интерес к зеркальным антеннам не ослабевает и в наши дни в связи со стремительным развитием космических радиотехнических систем и комплексов.
Достаточная простота и легкость конструкции, возможность формирования самых разнообразных диаграмм направленности, высокий КПД, малая шумовая температура – вот основные достоинства, зеркальных антенн, обуславливающих их широкое применение в современных радиосистемах.
Целью данной курсовой является освоение методики проектирования зеркальных параболических антенн: определение их основных электродинамических параметров и конструктивный расчет.
В курсовой работе определение поля излучения параболической антенны производится апертурным методом, который широко применяем при проектировании зеркальных антенн.
1 РАСЧЕТ ГЕОМЕТРИЧЕСКИХ И ЭЛЕКТРОДИНАМИЧЕСКИХ ПАРАМЕТРОВ ОБЛУЧАТЕЛЯ И ПАРАБОЛОИДА
1.1 Выбор фидера. Определение шумовой температуры фидерного тракта
В качестве фидера будет использован прямоугольный волновод. Его параметры для частоты f = 1.0 ГГц даны в (1), приложение А:
![]() см
см
a = 0.00405 дБ/м
Шумовая температура фидерного тракта Тф:
![]() ,
,
где α – коэффициент затухания линии передачи (дБ/м),
lф – длина фидерной линии (м).
![]() .
.
Выразим КПД из формулы:
Тф=T0·(1-КПД),
где Т0=290К.
Тогда КПД равен:
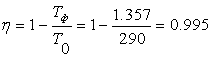 .
.
Шумовая температура антенной системы:
![]()
a1 = 1 - cosn+1Y0 = 0.929 (см. пункт 1.4)
![]() К;
К;
![]() К.
К.
1.2 Определение диаметра раскрыва
Зеркальная антенна – направленная антенна, содержащая первичный излучатель и отражатель антенны в виде металлической поверхности. Параболическая зеркальная антенна представлена на рисунке 1.
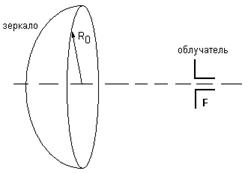
Рисунок 1 – Зеркальная параболическая антенна
В случае равномерно возбуждённого раскрыва параболического зеркала ширина ДН приближённо определяется:
![]() ,
,
где 2Q0.5 – ширина диаграммы направленности на уровне половинной мощности, рад.;
l - длина волны излучаемого (принимаемого) антенной радиосигнала;
R0 – радиус раскрыва зеркала (рисунок 1).
Длина волны определяется по формуле:
![]() cм.
cм.
Неравномерное возбуждение раскрыва зеркала приводит к некоторому расширению главного лепестка ДН, так как уменьшается эффективная площадь раскрыва. Чаще всего диаграммы направленности зеркальных антенн не обладают осевой симметрией, т.е. ширина главного лепестка в плоскостях Е и Н различна. В большинстве практических случаев это влечёт за собой следующее изменение:
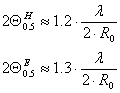
где 2QН0.5 , 2QЕ0.5 ширина ДН соответственно в плоскостях H и E.
Для Е и Н плоскостей соответственно найдем радиусы раскрыва:
![]() м;
м;
![]() м.
м.
Исходя из исходных данных о ширине диаграммы направленности в обеих плоскостях, можно определить диаметр раскрыва dp= 2 × R0, причем, из полученных двух значений диаметра следует выбрать наибольшее. Следовательно,
R0 = 3.673 м,
dp= 2×R0 = 2×3.673 = 7.346 м.
1.3 Аппроксимация аналитического вида ДН облучателя функцией вида cosn/2Y
В зависимости от размещения облучателя относительно зеркала можно получить то или иное значение КНД. При определенном оптимальном отношении Ro/fo КНД наибольший. Это объясняется тем, что количество теряемой энергии зависит от формы диаграммы направленности облучателя и от отношения Ro/fo. При уменьшении отношения Ro/fo от оптимального КНД уменьшается, так как увеличивается часть энергии, проходящей мимо зеркала. С другой стороны, увеличение этого отношения также приводит к уменьшению КНД в связи с более сильным отклонением закона распределения возбуждения от равномерного. Оптимальное значение Ro/fo определяется по аппроксимированной нормированной ДН облучателя (аппроксимация функцией вида F(Q)=cosn/2(Q), где n определяет степень вытянутости ДН облучателя).
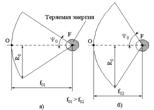
Рисунок 2 - Варианты размещения облучателя
Для вибратора с контррефлектором в виде диска:
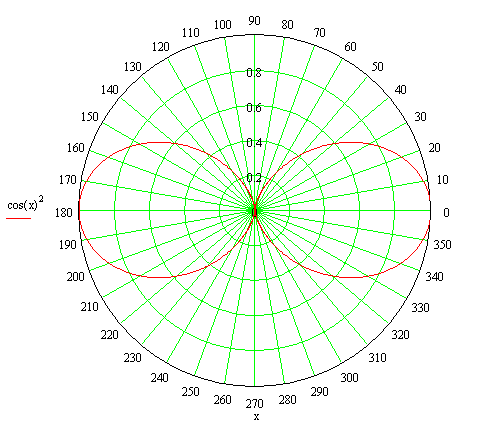
n=4; R0/f0=1.0…1.25; ν=0.82
![]()
Аппроксимированная нормированная ДН представлена на рисунке 3.
|