Измерение вязкости
1.1 Метрология. Исторические аспекты метрологии
Наука начинается тогда, когда начинают измерять.
Д.И. Менделеев
Проблема обеспечения единства измерений имеет возраст, сопоставимый с возрастом человечества. Как только человек стал обменивать или продавать результаты своего труда, возник вопрос - как велик эквивалент этого труда и как велик продукт, представленный на обмен или продажу. Для характеристики этих величин использовались различные свойства продукта - размеры,- как линейные, так и объемные,- масса или вес, позднее цвет, вкус, состав и т. д. и т. п. Естественно, что в давние времена еще не существовало развитого математического аппарата, не было четко сформулированных физических законов, позволяющих охарактеризовать качество и стоимость товара. Тем не менее проблема справедливой сбалансированной торговли была актуальна всегда. От этого зависело благосостояние общества, от этого же возникали войны.
Первыми средствами обеспечения единства измерений были объекты, которые имеются в распоряжении человека всегда. Так появились первые меры длины, опирающиеся на размеры рук и ног человека. На Руси использовались локоть, пядь, сажень, косая сажень. На Западе - дюйм, фут, сохранившие свое название до сих пор. Поскольку размеры рук и ног у разных людей были разными, то должное единство измерений не всегда удавалось обеспечить. Следующим шагом были законодательные акты различных правителей, предписывающие, например, за единицу длины считать среднюю длину стопы нескольких людей. Иногда правители просто делали две зарубки на стене рыночной площади, предписывая всем торговцам делать копии таких «эталонных мер». В настоящее время такую меру можно видеть на Вандомской площади в Париже в том месте, где когда-то располагался главный рынок Европы.
По мере развития человечества и науки, особенно физики и математики, проблему обеспечения единства измерений стали решать более широко. Появились государственные службы и хранилища мер, с которыми торговцам в законодательном порядке предписывалось сравнивать свои меры. Для определения размеров единиц выбирались размеры объектов, не изменяющиеся со временем. Например, для определения размера единицы длины измерялся меридиан Земли, для определения единицы массы измерялась масса литра воды. Единицы времени с давних времен до настоящего момента связывают с вращением Земли вокруг Солнца и вокруг собственной оси.
Дальнейший прогресс в обеспечении единства измерений состоял уже в произвольном выборе единиц, не связанных с веществами или объектами. Это связано с тем фактом, что изготовить копию меры (передать размер единицы какой-либо величины) можно с гораздо более высокой точностью, чем повторно независимо воспроизвести эту меру. В самом деле, точность определения длины меридиана и деления его на 40 миллионов частей оказывается очень невысокой. Подробно к этому мы вернемся при определении основных понятий и категорий метрологии. Здесь в кратком историческом экскурсе интересно вспомнить, что программа измерения длины парижского меридиана оказалась более полезной в составлении подробных карт перед наполеоновскими войнами, чем в точном определении единицы длины.
Гигантский скачок в точности измерений механических величин был совершен при внедрении лазеров в измерительную технику. Образно говоря, точность средств измерения стала определяться параметрами отдельного атома. Если выбрать определенный тип атома, определенный изотоп элемента, поместить атомы в резонатор лазера и использовать все преимущества, присущие лазерному излучению, то реально достижимая погрешность воспроизведения единицы длины может сказываться в тринадцатом-четырнадцатом знаках.
История развития науки об обеспечении единства измерений может быть прослежена не только на совершенствовании точности и единообразия определения какой-то одной единицы. Важным моментом является количество единиц физических величин, их отнесение к основным или производным, а также исторический аспект образования дольных и кратных единиц.
По мере совершенствования физики и математики появилась проблема измерения нового класса физических величин. Так при развитии теории электричества встал вопрос - как быть с единицами электромагнитных величин? С одной стороны, новый класс явлений подсказывал необходимость введения новых единиц и величин. С другой - исходно была установлена связь между электромагнитными явлениями и эффектами механическими - законы Кулона и Био-Савара-Лапласа. Точки зрения наиболее авторитетных ученых по этому поводу также разделились. Некоторые считали, что «рассмотрение (электромагнитных явлений) будет более плодотворным, если ввести четвертую, не зависящую от механических единицу» (А. Зоммерфельд). Другие, напротив, считали различные проявления свойств материи единым целым и были противниками введения независимых электрических величин и единиц. В результате в практике появились системы единиц физических величин, имеющие различное число основных, т. е. произвольно выбранных, физических величин. Подробно на этом мы остановимся в разделе, посвященном единицам физических величин.
С исторической точки зрения интересно обратить внимание на сложившуюся практику образования дольних (более мелких) и кратных (более крупных) единиц физических величин. В настоящее время мы пользуемся в основном десятичной системой счета, и действующая международная система единиц физических величин предписывает образовывать дольные и кратные единицы, домножая размер основной единицы на множитель, кратный десяти. Тем не менее история знает использование самых разнообразных множителей кратности. Например, сажень как мера длины равнялась трем аршинам, 1 фут равнялся 12 дюймам, 1 аршин - 16 вершкам, 1 пуд - 40 фунтам, 1 золотник - 96 долям, 1 верста - 500 саженям и т.д.
Такая исторически сложившаяся практика образования дольных и кратных величин оказалась крайне неудобной. Поэтому при принятии международной системы единиц СИ на эту проблему обращалось особое внимание. По большому счету десятичная система оказалась неудобной только при исчислении времени, т. к. единицы одноименной величины разного размера оказались кратными 12 (соотношение года и месяца) и 365,25 (соотношение года и суток). Эта кратность обусловлена скоростью вращения Земли и фазами Луны и является наиболее естественной. Дальнейшая замена кратности в соотношении час-минута и минута-секунда с 60 на кратное 10 уже особого смысла не имела. Из других часто употребляемых физических величин и единиц отступления от десятичной системы сохранилось в градусной мере угла, когда окружность делится на 360 градусов, а градус на минуты и секунды.
Совершая исторический экскурс в метрологию, не следует забывать, что все сказанное в полной мере относится только к странам-участницам Метрической конвенции. Во многих странах до сих пор сохраняется своя особая, иногда экзотическая система физических величин и единиц. Среди этих стран, как это ни странно, находятся Соединенные Штаты Америки - современная супердержава. Внутри этой страны до сих пор в обиходе величины и единицы старой Англии. Даже температуру там принято измерять в градусах Фаренгейта.
В связи с вышеизложенным знакомство с системами единиц, отличными от системы СИ, знакомство с различными системами счета единиц при измерениях в настоящее время носят не только познавательный характер. При расширении международных контактов может оказаться так, что знание альтернативных систем величин и единиц сослужит пользователю добрую службу.
При изложении основополагающих моментов, относящихся к системе СИ и при рассмотрении отдельных видов измерений мы иногда будем возвращаться к историческим корням выбора тех или иных физических величин. Сейчас важно помнить, что рассматриваемая проблема оптимального выбора физических величин и единиц будет существовать всегда, так как научно-технический прогресс постоянно предоставляет новые возможности в практике измерений. Сегодня это лазеры и синхротронное излучение, и завтра, возможно, появятся новые горизонты, опирающиеся на «теплую сверхпроводимость» или какое-либо замечательное достижение человеческой мысли.
1.2Основные понятия и категории метрологии
Прежде чем рассматривать различные методы, обеспечивающие единство измерений, необходимо определить основные понятия и категории. Поэтому в метрологии очень важно правильно использовать термины, необходимо определить, что именно подразумевается под тем или иным названием.
Физическая величина. Под этим определением подразумевается свойство, общее в качественном отношении многим объектам, но в количественном отношении индивидуальное для каждого объекта. Или, следуя Леонарду Эйлеру, «величиной называется все, что способно увеличиваться или уменьшаться, или то, к чему можно нечто прибавить или отчего можно отнять».
Вообще понятие «величина» многовидовое, т. е. относящееся не только к физическим величинам, являющимся объектами измерения. К величинам можно отнести количество денег, идей и т. п., т. к. к этим категориям применимо определение величины. По этой причине в стандартах (ГОСТ-3951-47 и ГОСТ-16263-70) приводится только понятие «физической величины», т. е. величины, характеризующей свойства физических объектов. В измерительной технике прилагательное «физическая» обычно опускается.
Единица физической величины - физическая величина, которой по определению придано значение, равное единице. Ссылаясь еще раз на Леонарда Эйлера: «Невозможно определить или измерить одну величину иначе, как приняв в качестве известной другую величину этого же рода и указав соотношение, в котором она находится к ней». Другими словами, для того чтобы охарактеризовать какую-либо физическую величину, нужно произвольно выбрать в качестве единицы измерения какую-либо другую величину того же рода.
Мера - носитель размера единицы физической величины, т. е. средство измерения, предназначенное для воспроизведения физической величины данного размера. Типичными примерами мер являются гири, рулетки, линейки. В других видах измерений меры могут иметь вид призмы, вещества с известными свойствами и т. д. При рассмотрении отдельных видов измерения мы будем специально останавливаться на проблеме создания мер.
Измерение - познавательный процесс, заключающийся в сравнении данной величины с известной величиной, принятой за единицу. Измерения подразделяют на прямые, косвенные, совокупные и совместные.
Прямые измерения - процесс, при котором искомое значение величины находят непосредственно из опытных данных. Простейшие случаи прямых измерений - измерения длины линейкой, температуры - термометром, напряжения - вольтметром и т. п.
Косвенные измерения - вид измерения, результат которых определяют из прямых измерений, связанных с измеряемой величиной известной зависимостью. Например, площадь можно измерить как произведение результатов двух линейных измерений координат, объем - как результат трех линейных измерений. Так же сопротивление электрической цепи или мощность электрической цепи можно измерить по значениям разности потенциалов и силы тока.
Совокупные измерения - это измерения, в которых результат находят по данным повторных измерений одной или нескольких одноименных величин при различных сочетаниях мер или этих величин. Например, совокупными являются измерения, при которых массу отдельных гирь набора находят по известной массе одной из них и по результатам прямых сравнений масс различных сочетаний гирь.
Совместными измерениями называют производимые прямые или косвенные измерения двух или нескольких неодноименных величин. Целью таких измерений является установление функциональной зависимости между величинами. Например, совместными будут измерения температуры, давления и объема, занимаемого газом, измерения длины тела в зависимости от температуры и т. д.
Средство измерения - техническое средство, используемое при измерениях и имеющие нормированные метрологические характеристики. В число средств измерений входят меры, измерительные приборы, измерительные установки, измерительные системы и преобразователи, стандартные образцы состава и свойств различных веществ и материалов. По временным характеристикам измерения подразделяются на:
- статические, при которых измеряемая величина остается неизменной во времени;
- динамические, в процессе которых измеряемая величина изменяется. По способу выражения результатов измерения подразделяются на:
o абсолютные, которые основаны на прямых или косвенных измерениях нескольких величин и на использовании констант и в результате которых получается абсолютное значение величины в соответствующих единицах;
o относительные измерения, которые не позволяют непосредственно выразить результат в узаконенных единицах, но позволяют найти отношение результата измерения к какой-либо одноименной величине с неизвестным в ряде случаев значением. Например, это может быть относительная влажность, относительное давление, удлинение и т. д.
Основными характеристиками измерений являются: принцип измерения, метод измерения, погрешность, точность, достоверность и правильность измерений.
Принцип измерений - физическое явление или их совокупность, положенные в основу измерений. Например, масса может быть измерена опираясь на гравитацию, а может быть измерена на основе инерционных свойств. Температура может быть измерена по тепловому излучению тела или по ее воздействию на объем какой-либо жидкости в термометре и т. д.
Метод измерений - совокупность принципов и средств измерений. В у помянутом выше примере с измерением температуры измерения по тепловому излучению относят к неконтактному методу термометрии, измерения термометром есть контактный метод термометрии.
Погрешность измерений - разность между полученным при измерении значением величины и ее истинным значением. Погрешность измерений связана с несовершенством методов и средств измерений, с недостаточным опытом наблюдателя, с посторонними влияниями на результат измерения. Подробно причины погрешностей и способы их устранения или минимизации рассмотрены в специальной главе, поскольку оценка и учет погрешностей измерений являются одним из самых важных разделов метрологии.
Точность измерений - характеристика измерения, отражающая близость их результатов к истинному значению измеряемой величины. Количественно точность выражается величиной, обратной модулю относительной погрешности, т. е.
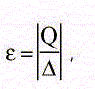">(1.1)
где Q - истинное значение измеряемой величины, Д - погрешность измерения, равная
">(1.2)
где Х - результат измерения. Если, например, относительная погрешность измерения равна 10-2%, то точность будет равна 104.
Правильность измерений - качество измерений, отражающее близость к нулю систематических погрешностей, т. е. погрешностей, которые остаются постоянными или закономерно изменяются в процессе измерения. Правильность измерений зависит от того, насколько верно (правильно) были выбраны методы и средства измерений.
Достоверность измерений - характеристика качества измерений, разделяющая все результаты на достоверные и недостоверные в зависимости оттого, известны или неизвестны вероятностные характеристики их отклонений от истинных значений соответствующих величин. Результаты измерений, достоверность которых неизвестна, могут служить источником дезинформации.
При выполнении различных работ по метрологическому обеспечению измерений используются специфические категории, которые тоже нуждаются в определении. Эти категории следующие:
Аттестация - проверка метрологических характеристик (погрешности измерений, точности, достоверности, правильности) реального средства измерения.
Сертификация - проверка соответствия средства измерения стандартам данной страны, данной отрасли с выдачей документа-сертификата соответствия. При сертификации кроме метрологических характеристик проверке подлежат все пункты, содержащиеся в научно-технической документации на данное средство измерения. Это могут быть требования по электробезопасности, по экологической безопасности, по влиянию изменений климатических параметров. Обязательным является наличие методов и средств поверки данного средства измерения.
Поверка - периодический контроль погрешностей показаний средств измерения по средствам измерения более высокого класса точности (образцовым приборам или образцовой мере). Как правило, поверка заканчивается выдачей свидетельства о поверке или клеймлением измерительного прибора или поверяемой меры.
Градуировка - нанесение отметок на шкалу прибора или получение зависимости показаний цифрового индикатора от значения измеряемой физической величины. Часто в технических измерениях под градуировкой понимают периодический контроль работоспособности прибора по мерам, не имеющим метрологического статуса или по встроенным в прибор специальным устройствам. Иногда такую процедуру называют калибровкой и это слово пишется на рабочей панели прибора.
Этот термин на самом деле в метрологии занят, и калибровкой согласно стандартам называют несколько иную процедуру.
Калибровка меры или набора мер - поверка совокупности однозначных мер или многозначной меры на различных отметках шкалы. Другими словами, калибровка - это поверка меры посредством совокупных измерений. Иногда термин «калибровка» употребляют как синоним поверки, однако калибровкой можно называть только такую поверку, при которой сравниваются несколько мер или деления шкалы между собой в различных сочетаниях.
2. Измерения механических величин
В технологических линейных измерениях наиболее часто востребованными являются следующие:
а) Толщины листовых материалов;
б) Толщины пленок (краска, влага, металл);
в) Глубина травления и гравирования;
г) Шероховатости поверхности;
д) Давления;
е) Вязкости ;
ж) Твердости;
з) Уровня жидкостей.
Традиционные измерения перемещений представляют собой хорошо известные линейки, нониусы и микрометрические винты. Линейки изготавливаются либо в виде жесткой конструкции, либо в виде гибкой ленты (рулетки). Измерения проводятся непосредственным сравнением размера предмета с делениями шкалы линейки. Нониус представляет собой дополнительную шкалу, нанесенную на подвижную каретку, перемещающуюся свободно вдоль линейки. Шкалы нониуса нанесены таким образом, что девять делений линейки разделены на десять равных частей.
Если проводить измерения, то имеется возможность определить размеры с точностью до 1/10 доли деления основной линейки. Для этого достаточно определить, какое деление нониуса совпадаете целым делением основной шкалы. Если, например, с делением основной шкалы совпадает первое деление нониуса, то это означает, что измеряемая длина на 1/10 часть деления основной шкалы больше того значения, у которого располагается нулевое деление нониуса. Если совпадает второе деление, то размер на 2/10 больше, и т. д.
Чаще всего используется так называемый прямой нониус, у которого цены деления на 1/10 часть меньше цены деления основной шкалы. Иногда применяют обратный нониус, у которого цена деления на 1/10 больше цены деления основной шкалы, т. е. 11 делений делятся на 10 частей. Пользоваться им следует также, как и прямым нониусом, т. е. целую часть измеряемой величины считывать с меньшего значения основной шкалы, между которыми остановился нуль нониуса, а десятые доли определять по совпадению деления шкалы нониуса с делением основной шкалы.
В некоторых измерительных инструментах, чаще всего в угломерных, применяется круговой нониус. Принципиально он ничем не отличается от линейного нониуса, только деления на нем нанесены на небольшую дуговую линейку (алиаду), свободно перемещающуюся вдоль основной шкалы (лимба).
Микрометрический винт дает возможность отсчитывать более мелкие доли деления основной шкалы, чем нониус. Микрометрический винт представляет собой тщательно изготовленный винт с шагом в 0,5 или в 1,0 мм. Головка винта представляет собой лимб, или барабан с делениями, позволяющий производить отчеты либо 1/50, либо 1/100 оборота. Таким образом, зажимая объект измерений между упорами микрометрического винта, можно измерить размеры объекта с точностью до 1/100 мм и выше, если принять во внимание возможность оценки доли деления.
Нониусом оснащены широко применяемые в измерительной практике инструменты, называемые штангенциркулями.
Микрометры изготавливают в виде скобы с цифрами, один из которых перемещается микрометрическим винтом.
Измерительные устройства для линейных измерений на какой-либо поверхности делают в виде индикаторных устройств, т. е. подвижных штоков с зубчатым колесом. Так сделаны глубиномеры, толщиномеры, ростомеры. Шток как бы «ощупывает» поверхность и, передавая перемещение зубчатому колесу, регистрирует профиль поверхности.
Толщину листовых материалов измеряют также по поглощению светового или (β-γ активного излучения. Иногда для измерения толщин используют емкостные или индуктивные датчики.
Толщины пленок измеряют оптическими методами по отражению или поглощению света.
Большое число измерений ведется лупами или измерительными микроскопами. Принцип измерения состоит в измерении координаты какой-либо точки, путем визирования ее в микроскоп. Длину объекта находят по разности отсчета крайних точек объекта. Небольшие перемещения можно измерить окуляр-микрометром - окуляром, снабженным визирной сеткой, расположенной в фокусе окуляра. Визирная сетка может перемещаться в поле зрения окуляра микрометрическим винтом.
Перемещая сетку винтом, наводят риски на крайние точки объекта, и размеры определяют как разность отсчетов.
Повысить точность измерения длин можно путем компарирования (сравнения) длин объекта и стандартной шкалы. Если эта шкала выполнена в виде линейки, то компарируются отсчеты по этой линейке. Для повышения точности в длинномерах - компараторах (например в приборе ИЗА-2) отсчет производится с использованием линейки, нониуса и микрометрического винта. Производится это следующим образом: в один из микроскопов визируется точка объекта, координаты которой нужно определить. В другой микроскоп - измерительный - визируются деления шкалы, нанесенной на стекло. Измерительный микроскоп позволяет визировать по крайней мере два деления на стеклянной шкале. Отсчет снимается с линейки, нониуса и микрометрического винта.
В современных компараторах длин измерения проводятся сравнением размеров объекта с размером измерительной дифракционной решетки. Принцип работы такого отсчетного устройства иллюстрируется.
Измерительная решетка представляет собой пару решеток, одна из которых может быть отражательной. За прозрачной решеткой располагается источник света и фоторегистрирующее устройство, например фотодиод. Перемещая одну из решеток, нужно регистрировать число проходящих в фокусе объектива максимумов или минимумов. Сравнивая это число для крайних точек объекта, легко найти его размеры, если известен шаг решетки.
Измерительные решетки в настоящее время вытесняют визуальные компараторы. Причин этому можно назвать несколько. Самая главная - процесс измерения легко автоматизировать, т. е. нет нужды пользоваться зрительной трубой, что для массовых измерений утомительно. Вторая причина - высокая точность измерения, определяемая только периодом решетки. При этом высокая точность получается как для малых перемещений, так и для больших (порядка 1 м и более). Еще одна привлекательная черта измерительных решеток - возможность создания реверсивных механизмов и подключения компьютеров.
Измерительные решетки в линейных измерениях используются как универсальные меры, т. е. носители размера физической величины. Большинство мер в линейных измерениях подразделяются на штриховые и концевые меры. Штриховые меры - это отрезки длины между какими-либо штрихами на линейках, нониусах и микрометрических винтах. В отличие от них концевые меры - это стержни, плитки, щупы, скобы точно известного размера. Существуют также концевые меры различных классов точности - от плиток Иогансона, служащих для поверки микрометров, до грубых щупов, широко используемых в машиностроении и в общей технике.
3. Измерения вязкости
Вязкость - характеристика сил внутреннего трения. Сила трения в зависимости от вязкости, жидкости или газа выражается формулой:
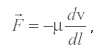">(1)
где F - сила сопротивления перемещению слоев среды, которая направлена в сторону убывания скорости (знак минус в формуле); S - площадь действия силы и 
">градиент скорости. Единица вязкости в системе СИ - Паскаль • секунда. В системе CGS единица вязкости - Пуаз:
">(2)
3.1 Вискозиметры
Приборы для измерения вязкости называются вискозиметрами. В вискозиметрах используются два разных принципа:
· по скорости вытекания жидкости из малого отверстия или из капилляра;
· по скорости падения шарика в вязкой жидкости.
Первый принцип основан на формуле Пуазейля, дающей зависимость между объемом жидкости, вытекающей из трубки радиусом R и длиной I:
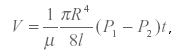">(1)
где P1 и P2 - давление на торцах трубки; R - радиус трубки; I - длина; t - время вытекания.
Второй принцип измерения вязкости основан на измерении скорости падения шара в вязкой среде (формула Стокса):
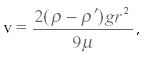">(2)
где v -скорость падения шара в жидкости; ρ - плотность материала шара; ρ' - плотность жидкости; r - радиус шара.
Одним из широко используемых приборов для измерения вязкости является вискозиметр Энглера, в котором измеряется время вытекания 200 г. жидкости по сравнению со временем вытекания 200 г воды через то же отверстие. Вязкость измеряют в градусах Энглера, что соответствует отношению времени вытекания жидкости ко времени вытекания воды при тех же условиях. Соотношение между Пуазами и градусами Энглера дается формулой:
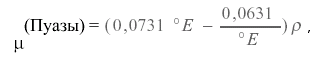">(3)
где р - плотность жидкости в г/см3.
Вязкость, обозначенная в формуле (3) и определенная через силу сопротивления движению называется еще динамической вязкостью. Существует понятие кинематической вязкости - это вязкость, отнесенная к единичной плотности, т. е.:
">(4)
Измеряется кинематическая вязкость в единицах L2T-1 , т. е. M2 /сек в системе СИ. Та же единица в СГС-системе называется стоксом, т. е.
">(5)
Существует еще понятие ударной вязкости, определяемой, как работа для излома твердого тела, отнесенная к единице поперечного сечения излома.
">(6)
Обратная вязкости величина называется текучестью:
">(7)
Иногда в технике пользуются понятием удельной вязкости, т. е. отношением вязкости жидкости к вязкости воды:
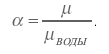">(8)
Вискозиметры Брукфильда подразделяются на три основных типа: аналоговые (с круговой шкалой), цифровые и программируемые. Основное различие между ними заключается в способе отображения результатов. У аналоговых вискозиметров результат считывается по указателю на круговой шкале, а у цифровых выводится на двухстрочный жидкокристаллический дисплей. Кроме того, цифровые вискозиметры оборудованы аналоговым выходом 0-10 мВ, к которому можно подключить различные внешние устройства, такие как дисплей, контроллер или самописец.
Внутреннее устройство аналоговых и цифровых вискозиметров практически одинаково и также одинакова методика использования. Оба типа представлены одинаковым рядом моделей, могут работать с одинаковыми аксессуарами и в целом взаимозаменяемы (одинаковые модели).
Аналоговые вискозиметры самые дешевые. Они идеально подходят для применений, где надо быстро измерить вязкость, но нет необходимости в постоянной записи или в измерении реологических характеристик. Хотя вискозиметр может работать непрерывно, снимать показания можно только дискретно, когда указатель проходит под смотровым стеклом или когда указатель зафиксирован и вискозиметр остановлен.
Длительные измерения требуют постоянного внимания оператора, кроме того, быстро протекающие процессы легче зафиксировать при постоянном мониторинге. В таких ситуациях лучше использовать цифровые вискозиметры, которые непрерывно измеряют и показывают вязкость. Такие приборы можно оставить без наблюдения, а возможность настроить частоту записи показаний (модель DV-II+) позволяет зарегистрировать самые быстрые реологические процессы. Некоторые пользователи предпочитаю цифровые вискозиметры, поскольку с ними отпадает необходимость интерполяции данных, чего иногда невозможно избежать при работе с аналоговым оборудованием. Точность измерения для обоих типов одинакова.
Цифровые вискозиметры (за исключением модели DV-E) можно также использовать с геометрией конус/плита.
Стандартные модели вискозиметров имеют множество модификаций, например модели с промежуточным крутящим моментом пружины. Чтобы подобрать модель, оптимальную для Ваших задач, лучше всего получить консультацию у местного представителя Брукфильда.
Некоторые модели разработаны специально для специфических применений и не совместимы с традиционными вискозиметрами. Так модель KU-1 позволяет измерять вязкость в единицах Кребса и предназначена для лакокрасочной индустрии. Модель САР-1000 позволяет работать с очень высокими скоростями сдвига (10000, 12000 с-1) при исследовании смол, полимеров и красок.
Весьма существенным преимуществом реометра DV-III+ является возможность двусторонней связи с персональным компьютером. Это позволяет легко программировать и управлять сложными процедурами измерения. Также можно сохранять все результаты и, при необходимости, преобразовывать их в формат Excel или другого табличного процессора. Можно получить результаты в виде графиков, что особенно полезно при интерпретации кривой течения. Графики испытания разных образцов можно сравнивать, накладывая друг на друга.
Реометр R/S отличается от других моделей тем, что контролируемым параметром является не скорость вращения шпинделя, а напряжение сдвига. Среди других преимуществ этого подхода можно выделить широкий диапазон измеряемой вязкости, возможность измерения предела текучести и возможность работы с высоковязкими гелями. Как DV-III+, так и R/S позволяют получить детальную информацию о поведении материалов и могут работать независимо или под управлением персонального компьютера.
Реометр САР-2000 с системой конус/плита обеспечивает широкий диапазон скоростей сдвига. Он специально сконструирован для использования в тяжелых заводских условиях и может работать независимо или под управлением персонального компьютера.
Реометр PVS обеспечивает измерение под давлением и обычно используется для исследования буровых растворов и флюидов для разрыва пласта в нефтегазовой индустрии.
Относительно новый реометр YR-1 является недорогим решением для измерения предела текучести в целях контроля качества.
Один из самых простых и недорогих автоматических вискозиметров - color control super digital производства flexologic
Ротационный вискозиметр полного погружения, производимый немецкой компанией opti-color
Принципиальная схема электромагнитных вискози - метров компании cambridge applied systems
3.3 Геометрия шпинделей
Все вискозиметры и реометры Брукфильда поставляются с набором шпинделей, пригодным для большинства стандартных применений. Однако нередки ситуации, когда необходимо использовать специализированные шпиндели. Брукфильд предоставляет широкий выбор шпинделей и аксессуаров для различных целей, большинство из них описано в данном разделе. Все шпиндели выполнены из нержавеющей стали марки 300 и не нуждаются в обслуживании. По заказу поставляются шпиндели для специальных применений, например для особо агрессивных сред.
1. Дисковые шпиндели.
Дисковые шпиндели входят в стандартный комплект поставки вискозиметров LV (шпиндели №2 и №3) и RV/HA/HB (шпиндели с №2 по №6) и предназначены для обычных измерений вязкости в сосудах емкостью от 600 мл и выше. Она обеспечивают точное и воспроизводимое измерение кажущейся вязкости большинства флюидов. 2. Цилиндрические шпиндели. Цилиндрические шпиндели (№1 и №4 для серии LV, №7 для серий RV/HA/HB) имеют определенную геометрию, позволяющую кроме вязкости рассчитать также скорость сдвига и напряжение сдвига. Во всех остальных аспектах они идентичны дисковым шпинделям. Благодаря определенной геометрии цилиндрические шпиндели частично пригодны для измерения не-Ньютоновских жидкостей. Доступны также цилиндрические эквиваленты дисковых шпинделей №12 и №3 серии LV. 3. Коаксиальные цилиндры.
Геометрия коаксиальных цилиндров обеспечивает их применение для тех задач, где обязательно нужно знать скорость сдвига и напряжение сдвига. Различные аксессуары Брукфильда имеют коаксиальную геометрию, кроме того каждый из них обеспечивает уникальные возможности для конкретных применений. Это следующие аксессуары:
адаптер для малых образцов SS;
адаптер для низкой вязкости UL;
адаптер для контроля температуры Thermosel;
адаптер DIN;
спиральный адаптер.
4. Конус/плита.
Геометрия конус/плита позволяет измерять абсолютную вязкость при определенных с высокой точностью скорости сдвига и напряжении сдвига. Требуемый объем образца очень мал и контроль температуры осуществляется очень просто. Данная геометрия идеально пригодна для изучения реологических характеристик не-Ньютоновских жидкостей и может быть использована совместно с вискозиметром Cone/Plate, реометром САР 2000 и реометром R/S (см. разд. 3.9). 5. Т-образные шпиндели.
Как правило эти шпиндели используются совместно со стойкой спирального движения (они входят в комплект поставки данного адаптера) и позволяют работать с нетекучими или слабо текущими материалами, такими как пасты, кремы и гели. Результаты измерения являются "кажущимися", поскольку особая геометрия шпинделей не позволяет определить скорость сдвига или напряжение сдвига.
6. Лопастные шпиндели.
Лопастной шпинель, погруженный в исследуемый материал, захватывает при вращении часть пробы и создает "цилиндр", позволяя рассчитать скорость сдвига и напряжение сдвига. Данный шпиндель позволяет производить исследования нетекучих и слабо текучих материалов и рассчитывать для них предел текучести. Лопастные шпиндели можно использовать совместно с большинством моделей вискозиметров Брукфильда.
3.4 Контроль температуры
Для получения точных и воспроизводимых результатов настоятель