Геометрии Галилея и Минковского как описания пространства-времени

Дипломная работа

«Геометрии Галилея и Минковского как описания пространства-времени» (факультатив для старших школьников)

В материалистической картине мира понятие пространства возникло на основе наблюдения и практического использования объектов, их объема и протяженности.

Понятие времени возникло на основе восприятия человеком смены событии, последовательной смены состояний предметов и круговорота различных процессов.

Естественнонаучные представления о пространстве и времени прошли длинный путь становления и развития. Самые первые из них возникли из очевидного существования в природе и в первую очередь в макромире твердых физических тел, занимающих определенный объем. Здесь основными были обыденные представления о пространстве и времени как о каких-то внешних условиях бытия, в которые помещена материя и которые сохранились бы, если бы даже материя исчезла. Такой взгляд позволил сформулировать концепцию абсолютного пространства и времени, получившую свою наиболее отчетливую формулировку в работе И. Ньютона «Математические начала натуральной философии» Этот труд более чем на два столетия определил развитие всей естественнонаучной картины мира. В нем были сформулированы основные законы движения и дано определение пространства, времени, места и движения.

Современное понимание пространства и времени было сформулировано в теории относительности А. Эйнштейна, по-новому интерпретировавшей реляционную концепцию пространства и времени и давшей ей естественнонаучное обоснование. Исходным пунктом этой теории стал принцип относительности, классический принцип относительности был сформулирован еще Г. Галилеем.

80 лет назад Герман Минковский предложил геометрическую интерпретацию специальной теории относительности. В наши дни знакомство с теорией относительности стало необходимым элементом общего образования, однако преподавание и понимание этой теории до сих пор затруднено тем, что ее математическое описание находится в противоречии с теми представлениями о пространстве и времени, которые базируются непосредственно на чувственных восприятиях и закрепляются в процессе изучения классической физики. Геометрия мира Минковского остается для неспециалистов труднодоступной абстракцией. Между тем к математическим знаниям, даваемым теперь средней школой и первым курсом вуза, надо добавить не много, чтобы развить представление о псевдоевклидовом пространстве. Прежде всего, требуется понятие абстрактного линейного пространства и его разновидности – евклидова пространства, умение различать линейные и метрические свойства пространства. Эти понятия являются исходными для построения геометрической теории. Без достаточно свободного владения ими и связанным с ними алгебраическим аппаратом нельзя преодолеть привязанность к привычной наглядности образов и проникнуть в мир форм, скрытых от непосредственного зрительного восприятия.

1. Геометрические представления Галилея

Исходным пунктом теории описания пространства стал принцип относительности, классический принцип относительности был сформулирован еще Г. Галилеем: во всех инерциальных системах отсчета движение тел происходит по одинаковым законам. Инерциальными называются системы отсчета, движущиеся друг относительно друга равномерно и прямолинейно.

Галилей разъяснял это положение различными наглядными примерами. Представим путешественника в закрытой каюте спокойно плывущего корабля. Он не замечает никаких признаков движения. Если в каюте летают мухи, они отнюдь не скапливаются у задней ее стенки, а спокойно летают по всему объему. Если подбросить мячик прямо вверх, он упадет прямо вниз, а не отстанет от корабля, не упадет ближе к корме.

Из принципа относительности следует, что между покоем и движением – если оно равномерно и прямолинейно – нет никакой принципиальной разницы. Разница только в точке зрения.

Например, путешественник в каюте корабля с полным основанием считает, что книга, лежащая на его столе, покоится. Но человек на берегу видит, что корабль плывет, и он имеет все основания считать, что книга движется и притом с той же скоростью, что и корабль. Так движется на самом деле книга или покоится?

На этот вопрос, очевидно, нельзя ответить просто «да» или «нет» Спор между путешественником и человеком на берегу был бы пустой тратой времени, если бы каждый из них отстаивал только свою точку зрения и отрицал точку зрения партнера. Они оба правы, и чтобы согласовать позиции, им нужно только признать, что книга покоится относительно корабля и движется относительно берега вместе с кораблем.

Таким образом, слово «относительность» в название принципа Галилея не скрывает в себе ничего особенного. Оно не имеет никакого иного смысла, кроме того, который мы вкладываем в утверждение о том, что движение или покой – всегда движение или покой относительно чего-то, что служит нам системой отсчета. Это, конечно, не означает, что между покоем и равномерным движением нет никакой разницы. Но понятия покоя и движения приобретают смысл лишь тогда, когда указана точка отсчета.

Если классический принцип относительности утверждал инвариантность законов механики во всех инерциальных системах отсчета, то в специальной теории относительности данный принцип был распространен также на законы электродинамики, а общая теория относительности утверждала инвариантность законов природы в любых системах отсчета, как инерциальных, и неинерциальных. Неинерциальными называются системы отсчета, движущиеся с замедлением или ускорением.

В соответствии со специальной теорией относительности, которая объединяет пространство и время в единый четырехмерный пространственно-временной континуум, пространственно-временные свойства тел зависят от скорости их движения. Пространственные размеры сокращаются в направлении движения при приближении скорости тела к скорости света в вакууме (300 000 км/с), временные процессы замедляются в быстродвижущихся системах, масса тела увеличивается.

Находясь в сопутствующей системе отсчета, то есть, двигаясь параллельно и на одинаковом расстоянии от измеряемой системы, нельзя заметить эти эффекты, которые называются релятивистскими, так как все используемые при измерениях пространственные масштабы и часы будут меняться точно таким же образом. Согласно принципу относительности, все процессы в инерциальных системах отсчета протекают одинаково. Но если система является неинерциальной, то релятивистские эффекты можно заметить и измерить. Так, если воображаемый релятивистский корабль типа фотонной ракеты отправится к далеким звездам, то после возвращения его на Землю времени в системе корабля пройдет существенно меньше, чем на Земле, и эта различие будет больше, чем дальше совершается полет, а скорость корабля будет ближе к скорости света. Разница может измеряться даже сотнями и тысячами лет, в результате чего экипаж корабля сразу перенесется в близкое или более отдаленное будущее, минуя промежуточное время, поскольку ракета вместе с экипажем выпала из хода развития на Земле.

Подобные процессы замедления хода времени в зависимости от скорости движения реально регистрируются сейчас в измерениях длины пробега мезонов, возникающих при столкновении частиц первичного космического излучения с ядрами атомов на Земле.

Итак, специальная теория относительности базируется на расширенном принципе относительности Галилея. Кроме того, она использует еще одно новое положение: скорость распространения света (в пустоте) одинакова во всех инерциальных системах отсчета.

Абсолютность скорости света не противоречит принципу относительности и полностью совместима с ним. Постоянство этой скорости " закон природы, а потому – именно в соответствии с принципом относительности – он справедлив во всех инерциальных системах отсчета.

Скорость света это верхний предел для скорости перемещения любых тел природы, для скорости распространения любых волн, любых сигналов. Она максимальна – это абсолютный рекорд скорости. Поэтому часто говорят, что скорость света – предельная скорость передачи информации. И предельная скорость любых физических взаимодействий, да и вообще всех мыслимых взаимодействий в мире.

Со скоростью света тесно связано решение проблемы одновременности, которая тоже оказывается относительной, то есть зависящей от точки зрения. В классической механике, которая считала время абсолютным, абсолютной является и одновременность.

В общей теории относительности были раскрыты новые стороны зависимости пространственно-временных отношений от материальных процессов. Эта теория подвела физические основания под неевклидовы геометрии и связала кривизну пространства и отступление его метрики от евклидовой с действием гравитационных полей, создаваемых массами тел. Общая теория относительности исходит из принципа эквивалентности инерционной и гравитационной масс, количественное равенство которых давно было установлено в классической физике. Кинематические эффекты, возникающие под действием гравитационных сил, эквивалентны эффектам, возникающим под действием ускорения. Так, если ракета взлетает с ускорением 2g, то экипаж ракеты будет чувствовать себя так, как будто он находится в удвоенном поле тяжести Земли. Именно на основе принципа эквивалентности масс был обобщен принцип относительности, утверждающий в общей теории относительности инвариантность законов природы в любых системах отсчета, как инерциальных, так и неинерциальных.

2. Геометрия Минковского как описание пространства – времени

Открытиями Коперника, Галилея, Кеплера, Ньютона заложен фундамент стройного естественнонаучного мировоззрения, которое позволило глубоко проникнуть в сущность вещей. Но на определенном этапе развития физической теории и точного эксперимента стали обнаруживаться расхождения между ними, свидетельствующие о наличии принципиальных недостатков в исходных теоретических предпосылках. Первоначально осознание этих недостатков и внесение поправок в теорию выразилось в постулатах, обобщающих новые экспериментальные факты. Из постулатов Эйнштейна развилась теория относительности, из постулатов Бора – квантовая теория – два главных направления революции в физике XX в. Эта научная революция, подобно коперниканской, внесла радикальные изменения в наши представления об устройстве мира.

Альберт Эйнштейн постулировал в качестве исходных истин такие утверждения, которые противоречили принципам классической физики, но не противоречили экспериментальным данным, и стал выяснять, какие поправки к классическим воззрениям вытекают логически из его постулатов. В первоначальной формулировке постулаты Эйнштейна гласят:

1. Законы, по которым изменяются состояния систем, не зависят от того, к которой из двух координатных систем, движущихся относительно друг друга равномерно и прямолинейно, эти изменения состояния относятся.

2. Каждый луч света движется в «покоящейся» системе координат с определенной скоростью V, независимо от того, испускается ли этот луч света покоящимся или движущимся телом» (19).

Из этих постулатов Эйнштейн сделал вывод, что длительность промежутка времени между двумя событиями и величина расстояния между двумя точками пространства должны быть разными в разных инерциальных системах координат, движущихся относительно друг друга. Парадоксальный вывод о непостоянстве пространства и времени (а вслед за ними и массы), считавшихся в классической физике фундаментальными абсолютными характеристиками мира, явился самой яркой чертой новой теории, что отразилось в закрепившемся за ней названии – теория относительности. До самого конца XIX в. в науке сохранялось убеждение в том, что мировое пространство в своей сущности таково, каким мы его воспринимаем посредством наших органов чувств. Самые характерные черты чувственно воспринимаемого пространства заключаются в том, что оно имеет три измерения и описывается геометрической теорией Евклида. По современной терминологии оно так и называется: трехмерное собственно евклидово пространство. Но если мировое пространство действительно таково, то расстояния между его точками (размеры и формы тел) должны быть инвариантными, не зависящими от выбора системы отсчета. Герман Минковский понял, что чувственно воспринимаемое пространство – это только внешняя видимость, форма проявления иных геометрических свойств реального мирового пространства. «Воззрения на пространство и время, которые я намерен перед вами развить, возникли на экспериментально-физической основе. В этом их сила. Их тенденция радикальна. Отныне пространство само по себе и время само по себе должны обратиться в фикции и лишь некоторый вид соединения обоих должен еще сохранить самостоятельность», – так начал Минковский свой доклад на 80-м собрании немецких естествоиспытателей и врачей в Кельне 21 сентября 1908 г. (9).

Как во времена Коперника трудно было принять вопреки внешней очевидности гелиоцентрическую систему мира, так в наше время нелегко понять и представить себе мир в пространстве, отличном от чувственно воспринимаемого. Для преодоления этого затруднения тоже необходимы познания из области геометрии, но более глубокие. Но было бы неправильно думать, что понимание геометрии мира Минковского доступно только специалистам с высшим физико-математическим образованием. В наши дни расширение и дифференциация научных знаний сопровождается обобщениями, вскрытием немногих глубочайших понятий и связей между ними, позволяющих строить точное и лаконичное изложение теории. Развитие геометрии в этом направлении идет по пути ее алгебраизации.

Глубина аксиоматических построений, используемых в линейной алгебре, позволяет не только упростить изложение известных геометрических истин, но и открывает новые возможности геометрических представлений. Если мы сможем выразить в немногих математических понятиях и соотношениях все существенные свойства чувственно воспринимаемого пространства, то поймем, как оно устроено, или, грубо говоря, каковы его основные «исходные компоненты». Тогда станет видно, как эти «компоненты» могут сочетаться в иных комбинациях, образуя иные типы пространств.

2.1 Основные понятия описания пространства-времени

2.1.1 Геометрические векторы и линейные операции над ними

Для математического описания пространства удобно пользоваться векторами. Этот объект достаточно прост и нагляден в чувственно воспринимаемом пространстве (где его называют геометрическим вектором) и вместе с тем пригоден для далеко идущих обобщений. Геометрическим вектором называется направленный отрезок, т.е. отрезок прямой, для которого указано, какая из его граничных точек является началом и какая концом (6).

Слово вектор происходит от латинского глагола vehere – перевозить, перемещать. Английское слово vehicle того же корня обозначает любое перевозочное средство от телеги до космического корабля (space vehicle) (5). Геометрический вектор указывает прямолинейный переход из одной точки пространства в другую. Из такого представления естественно вытекает определение операции сложения векторов (рис. 1). Если выполнить переход из точки О в точку А, выражаемый вектором , а затем добавить к нему переход из точки А в точку S, выражаемый вектором , то результат двух переходов будет таким же, как прямолинейный переход из точки О в точку S, выражаемый вектором . Поэтому вектор s называют суммой векторов а и b и записывают операцию сложения векторов в виде алгебраического выражения

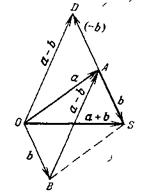
Рис. 1

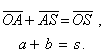(2.1)

Такой способ построения суммы векторов называют правилом треугольника.

Два вектора считаются равными, если посредством параллельного переноса можно совместить точки их начала и конца соответственно. При таком определении равенства векторов становится безразлично, в какой точке приложен вектор (какова точка его начала), и возникает понятие свободного вектора. Свободный вектор не имеет определенной точки начала, и мы имеем право представлять его приложенным в любой точке пространства по своему желанию. Совмещая на рис. 1 начало свободного вектора b с началом вектора а, построим параллелограмм OASB, для которого суммарный вектор является диагональю, исходящей из общего начала складываемых векторов. Такой способ построения суммы векторов называется правилом параллелограмма.

Оба правила (треугольника и параллелограмма) выявляют важное свойство суммарного вектора – он лежит в одной плоскости с векторами-слагаемыми. Пользуясь латинским термином, говорят, что складываемые векторы и суммарный вектор компланарны («соплоскостны»). Для свободных векторов понятие компланарности расширяется: компланарные векторы могут и не лежать в одной плоскости, но существует плоскость, которой параллельны все они и в которую при желании их можно привести посредством параллельного переноса.

Частным случаем перехода из одной точки пространства в другую является отсутствие перехода. Тогда точка конца геометрического вектора совпадает с точкой его начала. Такой вектор называют нулевым и обозначают символом 0. Очевидно соотношение

(2.2)

которое служит алгебраическим определением нулевого вектора.

2.1.2 Псевдоевклидова плоскость

Мир Минковского четырехмерен, но увеличение размерности – не самая главная трудность на пути овладения этим понятием. Гораздо труднее преодолеть барьер необычности метрических свойств пространства Минковского. На первый взгляд они кажутся фантастическими. И если даже математика ручается за их логическую непротиворечивость, остается впечатление, что здесь речь идет о такой математической абстракции, которой нет места в природе. Репутация нереальности метрики мира Минковского тесно связана с сохраняющимся в качестве пережитка представлением о нереальности комплексных чисел, чему сильно способствует и терминология («мнимые» числа). Вот почему необходим небольшой экскурс в эту область.

На протяжении истории науки понятие числа развивалось, приобретая все большую общность. И теперь каждому человеку при получении математического образования приходится в сжатом виде повторять этот процесс расширения понятия числа.

В простейшем представлении число есть количество предметов. Такому представлению соответствует понятие натурального числа (целого положительного). Множество N натуральных чисел замкнуто относительно операций сложения и умножения. Это значит, что, складывая или перемножая любые натуральные числа, мы необходимо будем получать в результате натуральные числа, т.е. не выйдем из множества N.

Операция деления натуральных чисел может привести к дроби, которая не является натуральным числом. Признание дробей числами не вызывало затруднений даже в древние времена. Этот выход за пределы множества N заставил расширить понятие числа. Числом стали называть не только количество предметов, но и отношение количеств.

Несравненно медленнее и труднее формировалось в науке понятие отрицательного числа. Сталкиваясь с необходимостью вычитать из меньшего числа большее, древние математики истолковывали решение как недостаток некоторого количества, но само это количество выражали положительным числом. У них не было числа, которым можно выразить результат такого, например, действия: 2–5 =… И когда они получали при решении уравнения отрицательный корень, то просто отбрасывали его как «недопустимый». «В Европе математики XVI в., хотя и пользовались иногда отрицательными числами, все же называли их «ложными» и «неясными», «меньше, чем ничто» и т.п.» (2). Лишь в XVII в., после того как Декарт ввел в употребление координатные системы и установил взаимно однозначное соответствие между числами и точками координатной оси, в математике окончательно утвердилось представление о равноправии положительных и отрицательных чисел. Сложилось понятие рационального числа как отношения любых целых чисел т та п. Множество Q рациональных чисел замкнуто относительно операций сложения и вычитания, умножения и деления.

Так потребность в увеличении набора операций, которые можно выполнять над числами, приводила к обобщению понятия числа. Сталкиваясь с задачами, решение которых не могло быть выражено числом в прежнем, узком его понимании, математики приходили к расширению множества объектов, заслуживающих названия числа, формировали новое, более емкое определение числа, включающее в себя и такие числа, которые считались прежде несуществующими или по крайней мере неполноценными. Объективная значимость нового, расширенного понятия числа заключается в том, что с его помощью удается более полно и логически непротиворечиво выражать отношения, существующие в природе.

Точки координатной оси, которым соответствуют рациональные числа, расположены всюду плотно. Это значит, что, сколь бы малый отрезок оси мы ни взяли, на нем найдется бесконечно много точек, служащих образами рациональных чисел. Вместе с тем на любом отрезке координатной оси имеется бесконечно много таких точек, которые не являются образами рациональных чисел. Классическим примером тому, поразившим древних математиков, является задача о сравнении длин стороны квадрата и его диагонали.

Выберем на прямой линии единицу измерения и построим квадрат ОАВС со стороной, равной этой единице. Отложив длину диагонали ОВ на координатной оси, получим отрезок OD (рис. 2). Его длина, очевидно, должна равняться отношению длин отрезков ОB и ОА:

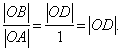
Между тем это отношение отрезков не может быть выражено никаким отношением целых чисел, т.е. никаким рациональным числом. Действительно, по теореме Пифагора имеем

Если допустить, что существуют такие целые числа m и n, отношение которых равно длине отрезка OD, выраженной в единицах :

то придем к противоречию. Мы вправе считать, что числа m и n не имеют общих множителей (при наличии общего множителя можно произвести сокращение на него и в дальнейшем рассматривать уже несократимую дробь). Кроме того, , т.е. не является целым числом, так как из неравенства следует . Возводя равенство в квадрат, мы

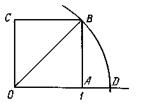
Рис. 2

получили бы . Но числа и не имеют общих множителей, поскольку их не имеют числа и n, причем . Значит, – несократимая дробь, которая не может равняться целому числу 2. Мы доказали, что не существует такого рационального числа, квадрат которого был бы равен 2 (1).

Если считать, что числа могут быть только рациональными, то нельзя выполнять операцию извлечения квадратного корня да числа 2 и символ следует признать лишенным смысла. Он обозначает нечто «потустороннее», не имеющее места в множестве чисел (рациональных чисел). Но такая точка зрения не согласуется с геометрическим содержанием рассмотренной задачи.

Ведь символ в данном случае выражает вполне реальную геометрическую величину – длину диагонали квадрата, сторона которого принята за единицу. Точка D (см. рис. 2), отстоящая на расстоянии этой длины от точки О, реально существует на координатной прямой ОА. Положение этой точки может быть указано приближенно с любой точностью посредством рациональных чисел, которые соответствуют границам сколь угодно малого отрезка, содержащего в себе точку D.

Немаловажно и следующее обстоятельство. Пусть есть только символ, которому не соответствует число (в смысле определения рационального числа). Но в ряде случаев операции над такими «потусторонними» объектами, выполняемые по правилам оперирования «настоящими» числами, могут приводить к вполне посюстороннему результату – рациональному числу. Например,

Подобные соображения настоятельно склоняли математиков к мысли, что символам , и т.д. соответствуют некоторые реальные числа, хотя они и не могут быть выражены в виде отношения целых чисел. Удивление перед этими «невыразимыми» числами отразилось в их названии – иррациональные числа, т.е. числа, не поддающиеся разумному истолкованию (racio – разум). Именно, в противовес иррациональным числам, числа, которые могут быть выражены в виде отношения целых чисел, получили название рациональных.

К концу XIX в. была построена теория, истолковывающая рациональные и иррациональные числа с единой точки зрения (теория сечений Дедекинда) (15). Объединение множеств рациональных и иррациональных чисел называется множеством вещественных (или действительных) чисел R. Каждому вещественному числу соответствует определенная точка на координатной оси, и каждой точке координатной оси соответствует определенное вещественное число.

Проблемы становления понятия вещественного числа поучительны для постижения еще более широкого представления о числе, каковым является число комплексное. Необходимость введения комплексных чисел связана с потребностью выразить результаты определенных операций над вещественными числами, не являющиеся вещественными числами. Не существует такого вещественного числа, квадрат которого был бы отрицательным числом. Поэтому в множестве вещественных чисел R нет квадратных корней (а следовательно, и корней любой четной степени) из отрицательных вещественных чисел. Так как квадрат любого вещественного числа есть неотрицательное число , символ удобно применять для обозначения любого отрицательного вещественного числа. Задача извлечения квадратного корня из числа сводится к задаче извлечения квадратного корня из отрицательной единицы:

От Леонарда Эйлера идет обычай обозначать символ буквой (начальной буквой французского слова imaginaire – мнимый, воображаемый):

(2.3)

Этот символ называют мнимой единицей. Тогда для квадратного корня из произвольного отрицательного вещественного числа получаем обозначение

, (2.4)

называемое «мнимым числом ».

В этом названии отразилось то представление, что корень квадратный из отрицательного числа не является числом в «реальном» смысле, что с символом если и связывается какое-либо понятие о числе, то о числе «не настоящем», «выдуманном», «в действительности не существующем». «Выдумка» в данном случае отстоит гораздо дальше от «реальности», подтверждаемой внешней видимостью, чем выдумка иррациональных чисел.

Каждому иррациональному числу, по крайней мере, соответствует определенная точка на координатной оси, а для мнимого числа не удается найти никакого геометрического истолкования или применения. Длины любых отрезков в чувственно воспринимаемом пространстве выражаются вещественными числами, и нет такого отрезка, для выражения длины которого потребовалось бы мнимое число.

Однако у мнимых чисел есть та важная, общая с иррациональными числами черта, что в некоторых случаях операции над символом iy, который не выражает вещественного числа, приводят все-таки к вещественным числам. Это, прежде всего операция возведения любого мнимого числа в квадрат:

. (2.5)

И более сложные выражения, составленные из мнимых величин, могут сводиться к функциям вещественного аргумента, принимающим вещественное значение. Например, если с учетом (2.5) сложить два бесконечных степенных ряда

то получится ряд, состоящий только из вещественных членов, сходящийся к функции 2 cos у:

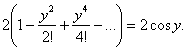
По мере того как углублялось исследование мнимых чисел и функций от мнимого аргумента, раскрывалась их важная роль в решении коренных теоретических проблем математики, а также прикладных задач. Все настоятельнее пробивало себе дорогу убеждение в противоестественности отношения к мнимому числу как к не реальному, «потустороннему» математическому объекту.

Даже в простейших задачах можно усмотреть признаки того, что мнимое число в органическом единстве с числом вещественным представляет некий аспект более глубокого и совершенного понятия числа.

Рассмотрим проблему существования решений некоторых квадратных уравнений. Если в уравнении

(2.6)

дискриминант отрицателен, то в множестве вещественных чисел R не найдется корней этого уравнения. В общем случае их нет и среди мнимых чисел, а лишь специфическое сочетание вещественных и мнимых чисел позволяет дать выражение корню. Например, применяя формулу решения квадратных уравнений

(2.7)

к уравнению

(2.8)

получим

(2.1.9)

Подставляя любое из этих выражений в уравнение (2.8) и выполняя действия обычным образом с учетом (2.5), придем к верным числовым равенствам:

Таким образом, есть основания считать выражения 2+3i и 2–3i корнями уравнения (2.8), хотя и нелегко понять, что они означают.

Операция сложения применяется в математике для весьма разнообразных классов объектов: вещественных чисел, векторов, матриц, операторов и т.д., но в каждом случае в роли слагаемых и суммы выступают элементы одинаковой природы. Не так получается с корнями уравнения (2.8). По смыслу общей формулы корней квадратного уравнения, каждый корень является суммой двух членов. Но если дискриминант отрицателен, второй член оказывается мнимым числом, тогда как первый член – число вещественное. Непонятно, как можно складывать столь различные объекты и что представляет собой их сумма, не являющаяся ни вещественным, ни мнимым числом. Впрочем, именно эта непонятная сумма и дает ключ к решению проблемы. Во-первых, с ней необходимо считаться, поскольку она выражает корни квадратного уравнения. Во-вторых, она объединяет в себе оба типа чисел – и вещественные, и мнимые. Так, может быть на вещественные и мнимые числа и следует смотреть как на составные части более сложного числового объекта? В отрыве друг от друга каждая из них имеет лишь ограниченное применение, а в едином комплексе они образуют более полноценное понятие числа. Если в таком комплексном числе мнимая составляющая равна нулю, мы воспринимаем число как вещественное, а если нулю равна вещественная составляющая, то мы воспринимаем комплексное число как мнимое. При сложении комплексных чисел отдельно складываются их вещественные компоненты и мнимые. Исторически сложился обычай обозначать мнимую компоненту с помощью множителя . При такой трактовке проблемы мы получаем вместо бессмысленного сложения вещественного числа мнимым сложение двух комплексных чисел (объектов одинаковой природы) и в качестве суммы их – тоже комплексное число:

В записи комплексного числа знак плюс (минус) перед мнимой компонентой отнюдь не означает, что не нужно прибавлять (вычитать) к вещественной компоненте. Просто это собственный знак мнимой компоненты, которая может быть положительной или отрицательной. Чтобы избавиться от иллюзии, будто вещественная и мнимая компоненты комплексного числа складываются, можно записывать их, разделяя точкой с запятой. Заодно можно отказаться и от символического множителя при мнимой компоненте. Достаточным признаком различий вещественной и мнимой составляющих послужит их paс положение в записи комплексного числа – на первом месте вещественная, а на втором мнимая.

(2.10)

Именно такая форма записи принята в современной теории комплексных чисел, хотя в практике вычислений сохраняется и исторически сложившаяся алгебраически форма . Если требуется указать комплексное число как единый объект, не различая в нем вещественную и мнимую компоненты, то пользуются однобуквенным обозначением

(2.11)

Запишем в этих обозначениях правило сложения комплексных чисел:

(2.12)

Когда мы убеждались в том, что комплексные числа и являются корнями квадратного уравнения (2.8), то перемножали комплексные числа (возводили в квадрат) по обычному правилу умножения многочленов с учетом соотношения. В общем виде это выглядит так:

Если же записывать комплексные числа не в алгебраической форме, а в виде упорядоченных пар чисел, то правило умножения примет вид

(2.13)

Это выражение нетрудно запомнить в следующей формулировке: первая компонента произведения равна разности произведений предшествующих членов комплексных сомножителей, записанных рядом, и последующих их членов, а вторая компонента равна сумме произведений внешних членов и внутренних .

Мы описали подход к понятию комплексного числа и арифметическим действиям с комплексными числами в качестве догадки, которая возникает при рассмотрении частной задачи решения квадратного уравнения с отрицательным дискриминантом. В определение комплексных чисел органически включается определение операций над ними: комплексные числа z представляют собой упорядоченные пары вещественных чисел , которые складываются по правилу (2.12) и перемножаются по правилу (2.13). Множество комплексных чисел принято обозначать буквой С.

Операции вычитания и деления комплексных чисел определяются как обратные операциям сложения и умножения. Разностью чисел и называется такое комплексное число z, которое удовлетворяет соотношению

Отсюда следует

(2.14)

Частным от деления на , , называется такое комплексное число z, которое удовлетворяет соотношению . Из этого условия нетрудно найти

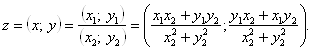(2.15)

Исходя из определения комплексных чисел и операций над ними, убедимся в том, что комплексные числа, у которых вторая компонента равна нулю, ведут себя в операциях так же, как вещественные числа:

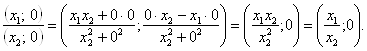
Результатами всех этих операц