Реальные системы и фазовые переходы
Фазами называют однородные различные части физико-химических систем. Однородным является вещество, когда все параметры состояния вещества одинаковы во всех его объемах, размеры которых велики по сравнению с межатомными состояниями. Смеси различных газов всегда составляют одну фазу, если во всем объеме они находятся в одинаковых концентрациях.
Одно и то же вещество в зависимости от внешних условий может быть в одном из трех агрегатных состояний – жидком, твердом или газообразном. В зависимости от внешних условий может находиться в одной фазе, либо сразу в нескольких фазах. В окружающей нас природе мы особенно часто наблюдаем фазовые переходы воды. Например: испарение, конденсация. Существуют такие условия давления и температуры, при которых вещество находится в равновесии в различных фазах. Например, при сжижении газа в состоянии равновесия фаз объем, может быть каким угодно, а температура перехода связана с давлением насыщенного пара. Температуры, при которых происходят переходы из одной фазы в другую, называются температурами перехода. Они зависят от давления, хотя и в различной степени: температура плавления – слабее, температура парообразования и сублимации – сильнее. При нормальном и постоянном давлении переход происходит при определенном значении температуры, и здесь имеют место точки плавления, кипения и сублимации (или возгонки.). Сублимация - это переход вещества из твердого состояния в газообразное можно наблюдать, например, в оболочках кометных хвостов. Когда комета находится далеко от солнца, почти вся ее масса сосредоточена в ее ядре, имеющем размеры 10-12 километров. Ядро, окруженное небольшой оболочкой газа – это так называемая голова кометы. При приближении к Солнцу ядро и оболочки кометы начинают нагреваться, вероятность сублимации растет, а десублимации – уменьшается. Вырывающиеся из ядра кометы газы увлекают за собой и твердые частицы, голова кометы увеличивается в объеме и становится газопылевой по составу.
2. Фазовые переходы первого и второго рода.
Фазовые переходы бывают нескольких родов. Изменения агрегатных состояний вещества называют фазовыми переходами первого рода, если:
1)Температура постоянна во время всего перехода.
2)Меняется объем системы.
3) Меняется энтропия системы.
Чтобы произошел такой фазовый переход, нужно данной массе вещества пообшить определенное количество тепла, соответствующего скрытой теплоте превращения. В самом деле, при переходе конденсированной фазы в фазу с меньшей плотностью нужно сообщить некоторое количество энергии в форме теплоты, которое пойдет на разрушение кристаллической решетки (при плавлении) или на удаление молекул жидкости друг об друга (при парообразовании). Во время преобразования скрытая теплота пойдет на преобразование сил сцепления, интенсивность теплового движения не изменится, в результате температура останется постоянной. При таком переходе степень беспорядка, следовательно, и энтропия, возрастает. Если процесс идет в обратном направлении, то скрытая теплота выделяется. К фазовым переходам первого рода относятся: превращение твердого тела в жидкое (плавления) и обратный процесс (кристаллизация), жидкого - в пар (испарение, кипение). Одной кристаллической модификации - в другую (полиморфные превращения). К фазовым переходам второго рода относится: переход нормального проводника в сверхпроводящее состояние, гелий-1 в сверхтекучий гелий-2, ферромагнетика – в парамагнетик. Такие металлы, как железо, кобальт, никель и гадолиний, выделяются своей способностью сильно намагничиваются и долго сохранять состояние намагниченности. Их называют ферромагнетиками. Большинство металлов (щелочные и щелочноземельные металлы и значительная часть переходных металлов) слабо намагничиваются и не сохраняют это состояние вне магнитного поля – это парамагнетики. Фазовые переходы второго, третьего и так далее родов связаны с порядком тех производных термодинамического потенциала ∂ф, которые испытывают конечные измерения в точке перехода, Такая классификация фазовых превращений связана с работами физика - теоретика Пауля Эрнеста (1880 -1933). Так, в случае фазового перехода второго рода в точке перехода испытывают скачки производные второго порядка: теплоемкость при постоянном давлении Cp=-T(∂ф2/∂T2), сжимаемость β=-(1/V0)(∂2ф/∂p2), коэффициент теплового расширения α=(1/V0)(∂2ф/∂Tp), тогда как первые производные остаются непрерывными. Это означает отсутствие выделения (поглощения) тепла и изменения удельного объема (ф - термодинамический потенциал).
Состояние фазового равновесия характеризуется определенной связью между температурой фазового превращения и давлением. Численно эта зависимость для фазовых переходов даётся уравнением Клапейрона-Клаузиуса: Dp/DT=q/TDV. Исследования при низких температурах – очень важный раздел физики. Дело в том, что таким образом можно избавиться от помех связанных с хаотическим тепловым движением и изучать явления в “чистом” виде. Особенно важно это при исследовании квантовых закономерностей. Обычно из-за хаотического теплового движения происходит усреднение физической величины по большому числу её различных значений и квантовые скачки “смазываются”.
Низкие температуры (криогенные температуры), в физике и криогенной технике диапазон температур ниже 120°К (0°с=273°К); работы Карно (работал над тепловым двигателем) и Клаузиуса положили начало исследованиям свойств газов и паров, или технической термодинамике. В 1850 году Клаузиус заметил, что насыщенный водяной пар при расширении частично конденсируется, а при сжатии переходит в перегретое состояние. Особый вклад в развитие этой научной дисциплины внес Реню. Собственный объем молекул газа при комнатной температуре составляет примерно одну тысячную объема, занимаемого газом. Кроме того, молекулы притягиваются друг к другу на расстояниях, превышающих те, с которых начинается их отталкивание.
3. Идеальный газ.
Идеальный газ, идеализированная модель газа; в идеальном газе силы взаимодействия между частицами (атомами, молекулами) пренебрежимо малы. К идеальным газам близки разряженные реальные газы при температурах, далеких от температуры и конденсации. Зависимость давления идеального газа от его температуры и плотности выражается уравнения Клапейрона, (Клаперона-Менделеева уравнение), найденная Б.П. Э. Клапейроном (1834) зависимость между физическими величинами, определяющими состояние идеального газа (давлением р, объемом V, и абсолютной температурой Т): PV=BT, где коэффициент В зависит от массы газов М и его молекулярной массы. Для одного моля идеального газа pV=RT, где R-газовая постоянная. Если молярная масса газа μ, то pV=M/μ *RT.
4. Реальный газ.
Реальный газ, отличается от идеального газа существованием взаимодействия между его частицами (молекулами, атомами). При малых плотностях наличие межмолекулярного взаимодействия учитывается вириальным уравнением состояния реального газа: pV=RT(1+B (T)/υ+C(T)/υ2+…), где р - давление, υ – молярный объем, Т – абсолютная температура, R – газовая постоянная, В(Т), С(Т) и так далее – вириальные коэффициенты, зависящие от температуры и характеризующие парные, тройные и так далее взаимодействия частиц в газе. Существуют и другие полуэмпирические и теоретические уравнения состояния реальных газов, например: уравнение Ван дер Ваальса (нидерландского физика), предложенное Ван дер Вальсом (1873г) уравнение состояния реального газа, учитывающее конечность объема молекул и наличие межмолекулярных сил притяжения; для одного моля газа имеет вид: (р+а/V2) (v-b)=RT, где р – давление, V – объем одного моля, T – абсолютная температура, R – универсальная газовая постоянная, a и b постоянные, характеризующие взаимодействие молекул данного вещества. Третье начало термодинамики: по мере приближения температуры к 0K. Энтропия всякой равновесной системе при изотермических процессах перестает зависеть от каких-либо термодинамических параметров состояния и в пределе (T=0K) принимает одну и туже для всех систем постоянную величину, которую можно принять равной нулю. Третье начало предсказывает вырождение идеальных азов при низкой температуре. Как показало развитие квантовой статистики, такое вырождение действительно имеет место. Оно указывает на недостаточность классической механики и основанной на ней классической статистики в области низких температур. Квантовая статистика показывает, что третье начало термодинамики является микроскопическим проявлением квантовых свойств реальных систем при низких температурах. Свойства реальных систем изучались экспериментально.
5. Молекулярно – кинетическая теория критических явлений.
Вскоре после открытия закона Бойля – Мариотта (произведение объема данной массы идеального газа на его давление постоянно при постоянной температуре; установлен независимо Р. Бойлем (1660г) и Э. Мариоттом (1676г)) были обнаружены отклонения от него: нидерландский физик Мартин Ван Марум установил, что при давлении 7 атмосфер газообразный аммиак переходит в жидкое состояние; примерно тогда же Лавуазье отметил роль охлаждения в изменении состояния газов. В середине прошлого века появились попытки учесть эти отклонения количественно, чтобы ввести поправки, но все они были случайными и не связывались с критическими состояниями газов. Ван-дер-Ваальс показал глубинную связь между жидким и газообразным состояниями вещества, объяснил их непрерывный переход друг в друга и развил молекулярно-кинетическую теорию критических явлений. Его теория позволила предсказать существование неустойчивых состояний вещества. После создания Гиббсом статистической механики наглядная теория Ван-дер-Ваальса была переведена на строгий математический язык. Гиббс дал развернутое изложение метода термодинамических потенциалов и его применение к анализу равновесия. С позиции своего метода он единым образом исследовал законы образования новой фазы, дал знаменитое правило фаз (в термодинамике: число равновесно сосуществующих в какой либо системе фаз не может быть больше числа образующих эти фазы компонентов плюс, как правило, 2). Установлено Дж. У. Гиббсом в 1873-1876гг, рассмотрел поверхностные и электрохимические явления, многокомпонентные системы и тому подобные. Развивая метод Гиббса, Дюгем в своих работах ввел термин «термодинамический потенциал». Гиббс пришел к идее введения таких функций после исследования поведения функции (Е-ТS+pV), когда заметил, что условие устойчивого равновесия сводится к равенству б(Е-ТS+рV)=0. Экстремальные значения этой функции оказались необходимыми и достаточными условиями равновесия систем при изобарно - изотермических процессах. В последствии эту функцию назвали изобарно – изотермическим потенциалом, или потенциалом Гиббса. Затем Гиббс установил, что термодинамические свойства системы можно описать еще тремя функциями, обладающими свойствами потенциалов – внутренней энергией (диабатический потенциал) и тепловой функцией (энтальпия). В химической термодинамике важен и химический потенциал, введенный Гиббсом.
С точки зрения статистической механики вывод уравнения состояния сводится к нахождению новой функции состояния свободной энергии F=E-TS как функции параметров p,T,V. Тогда уравнение состояния находится как p=-I∂I±I∂VIT. Нужно было найти свободную энергию системы, вычислив соответствующий интервал, что было непростой задачей. Гиббс понимал, что для полного описания системы, даваемого термодинамическими потенциалами, нужно знание молекулярной структуры и характера взаимодействия частиц. Поэтому он разработал метод нахождения статистических аналогов для изотермического и химического потенциалов. Метод Гиббса был пригоден для любых систем, но математические трудности того времени не позволяли уйти от идеализированных моделей.
6. Сверхтекучесть.
В 1945 году известный советский математик и физик-теоретик Н. Н. Боголюбов, разработавший более совершенный метод решения проблем статистической физики, привел уравнения состояния реальных газов в виду: p=(NkT/V)(1=NB1(T)/V+N2B2/V2+N3B3/V3+…..), где B – функции температуры, называемые вириальными коэффициентами, которые определяются по законам взаимодействия молекул. при низких температурах становится возможным наблюдать микроскопические квантовые явления – сверхпроводимость и сверхтекучесть. Сверхтекучесть – это свойство квантовых жидкостей – течь без трения. Впервые обнаружено в 1938 году советским ученым П.Л.Капицей в жидком гелии. При температурах ниже 2,17 К вязкость гелия обращается в ноль, и он свободно протекает через очень узкие капилляры. Теоретическое объяснение явления сверхтекучести было дано в 1941 году советским ученым Л.Д.Ландау (Ландау Лев Давидович (1908 - 1968), российский физик-теоретик, основатель научной школы, академик АН СССР (1946), Герой Социалистического Труда (1954)). Труды во многих областях физики: магнетизм; сверхтекучесть и сверхпроводимость; физика твердого тела, атомного ядра и элементарных частиц, физика плазмы; квантовая электродинамика; астрофизика и др.
Автор классического курса теоретической физики (совместно с Е. М. Лифшицем). Ленинская премия (1962), Государственная премия СССР (1946, 1949, 1953), Нобелевская премия (1962). По теории Ландау, необычность гелия состоит в следующем: жидкий гелий существует в двух формах. В области температур от 4,2 до 2,18 К (так называемая l- точка) он ведёт себя как классическая жидкость – это гелий. Ниже l- точки он состоит, как бы из двух жидкостей одна ведёт себя как гелий-1, другая проявляет свойства сверхтекучести – проводит тепло без потерь, то есть. Её теплопроводность равна бесконечности. Не оказывает сопротивления течению, или имеет нулевую вязкость, - это гелий-2. В l- точке происходит фазовый переход между состояниями гелия. Относительное количество каждой из компонент гелия зависит от температуры, причем его можно определить измерением силы, действующей на предмет, движущийся в жидкости. Опыты показывают, что при температуре ниже 1К практически весь гелий, находящийся в сверхтекучем состоянии. Атомы жидкого гелия образуют единую квантовую систему, энергию и импульс которой можно изменить только сразу на конечную величину, скачком. Поэтому до определенной скорости жидкий гелий течёт без трения, не замечая препятствий, - обладает свойством сверхтекучести. Сверхтекучесть является коллективным эффектом. Атомы гелия имеют целый (нулевой) спин и поэтому скапливаются в одинаковых состояниях. В результате квантовые свойства каждой частицы усиливаются. Спин. Элементарные частицы – это маленькие вращающиеся волчки. Они характеризуются моментом количества движения, или, кратко, угловым моментом. Согласно квантовой механике, угловой момент системы может принимать не любые значения: его скачки равняются постоянной Планке ħ (1,054*10-34*Дж*с), угловой момент элементарных частиц естественно измерять в единицах Планке. Момент, измеренный в таких единицах, называется спином. Спин гелия-4 атома гелия равен нулю, является бозоном, подчиняется статистике Бозе-Энштейна и поэтому не подчиняется запрету Паули (Согласно принципу Паули: в каждом квантовом состоянии может находиться только один электрон.), а изотоп гелия гелий-3, являющийся фермионом, подчиняется запрету Паули и не дает явления сверхтекучести. При понижении температуры гелия энергия его атомов, естественно, уменьшается. При какой-то очень низкой температуре все они окажутся в самом низком энергетическом состоянии, поскольку запрет Паули для них не применим. И будут иметь одинаковые волновые функции. Атомы сверхтекучего гелия ведут себя согласованно, как единое целое. Беспорядка в этой системе нет, энтропия равна нулю.
7. Сверхпроводимость.
Сверхпроводимость – весьма необычный феномен, отличающийся от всего того, к чему мы привыкли. Буквально это явление из иного мира. Мы живем в классическом мире, а сверхпроводимость явление квантовое, но в макроскопических масштабах. Например, волновые функции в квантовой механике вводят искусственно, а в сверхпроводимости они выступают естественным образом как измеримые величины.
7.1 Открытие сверхпроводимости.
| свойства сверхпроводников | применение | ||
| Создание магнитного поля | Передача электроэнергии | Обработка информации | |
| Нулевое электрическое сопротивление | + | + | + |
| Большие передаваемые токи | + | + | - |
| Большое магнитное поле | + | - | - |
| Фазовый переход | - | - | + |
| Квантовые эффекты | - | - | + |
Сверхпроводимость наблюдалась впервые при охлаждении ртути в 1911 году голландским ученым Гейке Каммерлинг-Оннесом. Исследования в области низких температур, первоначально имевшие чисто практическую направленность, при температуре 7,2 K сопротивление свинцового проводника внезапно снизилось в миллионы раз и практически исчезло.
Это странное явление получило название сверхпроводимости. Явление сверхпроводимости можно понять и обосновать только с помощью квантовых представлений. Почти полвека сущность этого явления оставалась нерасшифрованной, из-за того, что методы квантовой механики еще не в полной мере использовались в физике твердого тела.
В одном из экспериментов в сделанном из чистого свинца кольце был наведен ток в несколько сотен ампер. Через год оказалось, что ток все еще продолжает идти в кольце, и величина его не изменилась, то есть сопротивление свинца было равно нулю! За открытие сверхпроводимости Камерлинг-Оннес был удостоен лауреата Нобелевской премии.
7.2 Электрон – фононное взаимодействие.
Явление сверхпроводимости и сверхтекучести представляют собой макроскопический квантовый эффект. Братья Фриц и Гейнц Лондон создали феноменологическую теорию сверхпроводимости. В 1950 году английский физик Герберт Фрелих разработал теорию сверхпроводимости, связав ее с электрон-фононным взаимодействием, поскольку электроны взаимодействовали через упругие колебания кристаллической решетки (которым и сопоставлялись квазичастицы - фононы). Рассмотрим подробнее механизм возникновения электронных пар, связанных силами притяжения, которые чаще называют куперовскими парам.
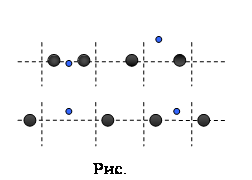 При движении электрона в сверхпроводнике при Т < Ткр. положительные ионы, находящиеся в узлах кристаллической решетки (пересечения пунктирных линий на рис.1), притягиваются к электрону, смещается от положения равновесия в его сторону. Последующее кулоновское отталкивание положительных ионов приводит к распространению по решетке упругой волны.
При движении электрона в сверхпроводнике при Т < Ткр. положительные ионы, находящиеся в узлах кристаллической решетки (пересечения пунктирных линий на рис.1), притягиваются к электрону, смещается от положения равновесия в его сторону. Последующее кулоновское отталкивание положительных ионов приводит к распространению по решетке упругой волны.