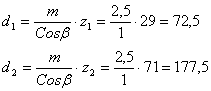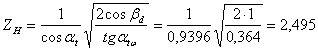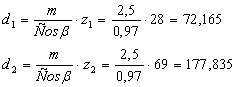Проектирование электродвигателя

Целью курсового проекта является практическое закрепление знаний по дисциплине и приобретение навыков проектирования основных узлов и деталей машин.

Объектом курсового проектирования являются механические передачи для преобразования вращательного движения, а также вращательного в поступательное. В рассматриваемом приводе представлены основные детали, кинематические пары и соединения. Здесь есть цепные и цилиндрические передачи, валы, оси, подшипники, соединительные муфты, соединения резьбовые, сварные, штифтовые, вал-ступица, корпусные детали, уплотнительные устройства и так далее. При проектировании редуктора находят практическое приложение такие важнейшие сведения из курса, как расчеты на контактную и объемную прочность, тепловые расчеты, выбор материалов и термообработок, масел, посадок, параметров шероховатости и так далее.

При выполнении проекта используются математические модели, базирующиеся на теоретических и экспериментальных исследованиях, относящиеся к объемной и контактной прочности, материаловедению, теплотехнике, гидравлике, теории упругости, строительной механике, трибонике и др. Широко используются также знания из курсов сопротивления материалов, теоретической механики, теории механизмов и машин, технологии машиностроения, машиностроительного черчения и др.

1. Выбор электродвигателя и энерго-кинематический расчет привода

Кинематическая схема привода общего назначения.

ЭД – электродвигатель

1 – цепная передача

2 – коническая передача

3 – цилиндрическая передача

Мощность на выходном валу привода: Р_вв=2,1кВт.

Частота вращения на выходном валу привода: n_вв=112об/мин.

Нагрузка постоянная.

Коэффициент перегрузки: К_п=1,45.

Срок службы привода: t=25000сек.

Энерго-кинематический расчет привода

Исходные данные для расчета:

Мощность на выходном валу: 2,1 КВт.

Частота вращения выходного вала: 112об/мин.

Нагрузка постоянная

Срок службы: 25000 часов.

1-цепная передача.

2-цилиндрическая косозубая передача.

3-цилиндрическая прямозубая передача.

Передачи 2 и 3 закрытые.

ЭД – электродвигатель.

Выбор параметров передач и элементов привода

Назначаем КПД (h) передач и элементов (подшипников) привода:

- цепная передача —0,96

- передача редуктора цилиндрическими зубчатыми колесами — 0,98

- подшипники качения (одна пара) — 0,995

Определяем ориентировочное (расчетное) значение КПД привода:

, где:

m - число пар подшипников качения в приводе (для данной схемы m=3)

Задаемся передаточными числами (U) передач привода:

- цепная передача — U₁=2

- зубчатая цилиндрическая передача(косозубая) — U₂=3

- зубчатая цилиндрическая передача (прямозубая)— U₃=3

Определяем передаточное число привода:

;

Определяем расчетную мощность электродвигателя:

Определяем потребную частоту вращения вала электродвигателя:

Выбираем электродвигатель с учетом расчетной мощности и потребной частоты:

марка электродвигателя —4А 90L4;; .

Определяем фактическое передаточное число привода:

Разбиваем фактическое передаточное число привода на передаточные числа передач привода с учетом рекомендаций и стандартного ряда на передаточные числа:

примем передаточное число цепной передачи — U^ст₁=2,0;

Т.к. редуктор двухступенчатый, то передаточные числа для цилиндрических передач определятся следующим образом:

прямозубая цилиндрическая передача (тихоходная) —

где

;

принимаю

;

косозубая цилиндрическая передача (быстроходная) —

;

Принемаю

Определяем фактическое передаточное число привода с учетом передаточных чисел принятых ранее:

;

Определяем фактическую частоту вращения выходного вала привода:

об/мин.

Определим погрешность и сравним с допускаемой в 5% :

Условие выполняется, переходим к следующему этапу расчета.

Определяем частоты вращения валов привода:

об/мин.

Определяем вращающие моменты на валах привода:

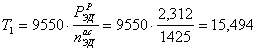Н·м.

Сводная таблица вращающих моментов и частот вращения валов привода:

вал	I	II	III	IV
n, об/мин.	1425	712,5	285	114
T, Н*м	15,494	29,6	72,157	175,901

Расчет цепной передачи

Исходные данные:

Частота вращения ведущей (малой) звездочки: n₁= 1425об/мин.

Частота вращения ведомой звездочки: n₂=712,5 об./мин.

Расчетная мощность двигателя: N = 2,312 кВт.

Передаточное число цепной передачи: u = 2,0.

Расчет:

Определяю число зубьев ведущей (малой) звездочки:

z₁=29-2u=29-2·2=25.

Принимаю число зубьев ведущей (малой) звездочки:

z1=25= z_табл=25…27,

где: z _табл=25…27.

Определяю число зубьев ведомой звездочки:

z₂=25·2 = 50

Определяю фактическое передаточное число цепной передачи:

Определяю отклонение от заданного передаточного числа:

Предварительно выбираю роликовую однорядную цепь нормальной серии.

Определяю шаг цепи P по следующей формуле:

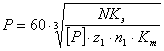где: К_э=К_д·К_а·К_н·К_рег·К_см·К_реж

Для однорядной цепи К_m= 1.

По таблицам выбираю коэффициенты:

К_Д=1– для спокойной нагрузки;

K_a=1;

K_H=1;

K_рег=1 - для передвигающихся опор;

К_см=1,5 – для периодического смазывания;

К_реж= 1,25 - для двухсменной работы.

К_э = 1·1·1,25·1·1,5·1,25 = 2,93

При n₁= 1425 мин^-1,(P) = 19,19МПа.:

Рассчитанное значение шага цепи округляю до стандартного Р=12,7 мм.

По табл. принимаю цепь ПР-12,7-900-1 ГОСТ 13568-75.

Определяю межосевое расстояние:

а=(30…50)·P=(30…50)·12,7=381…635 мм

Принимаю среднее значение межосевого расстояния:

а = 508 мм.

Определяю число звеньев цепи:

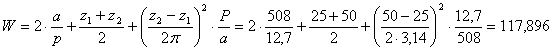
Принимаю целое число звеньев цепи:

W = 118

Определяю фактическое межосевое расстояние:

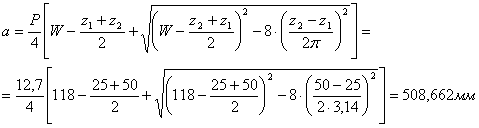
Определяю монтажное межосевое расстояние:

а_м=0,997·а=0,997·508,662=507,136 мм.

Определяю скорость цепи:

По табл. определяю, что данная цепная передача работает с циркуляционной под давлением смазкой, значит К_см=0,8

Рассчитываю геометрические параметры цепной передачи.

Рассчитываю делительный диаметр:

Рассчитываю диаметры окружности выступов:

D_e₁=P (0,5+ctg (180^º/z₁)=12,7(0,5 + ctg (180⁰/25)) = 106,881 мм.

D_e2=P (0,5+ctg (180^º/z₂)=12,7(0,5 + ctg (180⁰/50)) = 208,211 мм.

Рассчитываю диаметры окружности впадин:

D_i₁=D_d₁-2r = 101,33– 2*3,944= 93,442мм.

D_i₂= D_d₂-2r = 202,26 – 2*3,944 = 194,372 мм.

Рассчитываю радиусы впадины:

r=0,5025d₁+0,05 = 0,5025*7,75 + 0,05 =3,944 мм.,

где: d₁=7,75 мм по табл. 4

Радиусы закругления зуба:

r₁=1,7d₁= 1,7*9,75 = 13,175мм.

h₁=0,8d₁= 0,8*7,75= 6,2 мм.

b₁=0,93 B_bh-0,15 = 0,93*2,4 – 0,15 = 2,082 мм.,

где:

Рассчитываю диаметры обода:

D_c₁=P·ctg(180^º/z₁)-1,2h = 12.7*ctg(180^º/25) - 1,2*10,0 = 88.531 мм.

D_c2=P·ctg(180^º/z₂)-1,2h = 12.7*сtg(180^º/50) – 1,2*10,0 = 189,861 мм.,

где: h=10,0мм.

Определяю окружную силу:

По табл. 11 (n)_max=2525 мин^-1 при P=12,7мм и n₁=1425мин^-1< (n)_max=

=2525 мин^-1.

Определяю число ударов:

по табл.12 (ν)=60 . Условие ν < (ν) выполняется.

Определяю удельное давление в шарнирах:

где: уточненное значение К_э=1·1·1,25·1,25·0,8·1,25 =1,563 и проекция опорной поверхности шарниров А=39,6

Условие р=12,103МПа. < (p) =19,19МПа. выполняется.

Значение (p) выбираю по таблице 8.

Определяю статистическую прочность цепи:

, где:

Q=9000H по табл.2;

q=0,3кг;

F_v=q*v = 0,3·7,54²= 17,055H;

F₀=9,81·K_f·q · a = 9,81·6,3·0,3·508,662·10^-3=9,431 H,

где: К_f=6,3 для горизонтальной передачи.

По табл.14 (n)=12,54

Условие n=27,017 > (n) =12,54 выполняется.

Определяю силу, действующую на опоры вала;

F_on=K_gF_t+2F_o= 1 ·306,631+2·9,431=325,493 H.

Определяю стрелу провисания цепи:

f=0,02·a=0,02·508,662=10,1732мм.

Расчет цилиндрической передачи

Так как редуктор соосный, расчёт закрытых передач начинаем с тихоходной ступени, то есть с прямозубой цилиндрической передачи.

Исходные данные:

Выбираем материалы для изготовления зубчатых колёс и способы термообработки:

Выбираем в зависимости от выходной мощности

Так как

N_ВЫХ =кВт,

тогда материалы зубчатых колес – Сталь 40Х.

Термообработка:

шестерни – улучшение, твердость Н₁ = (269…262)=265НВ;

колеса – улучшение, твердость Н₂ = (235…262)=250НВ.

u = 2,5 – передаточное число.

n₁ = 285об/мин – частота вращения шестерни,

n₂ = 114об/мин – частота вращения колеса,

T₁ = 72,157 Н∙м – вращающий момент на шестерне,

T₂ = 175,901 Н∙м – вращающий момент на колесе,

Коэффициент перегрузки при пуске двигателя К_пер = 1,45.

1. Выбираем коэффициент ширины зуба y_ba с учетом того, что имеем несимметричное расположение колес относительно опор: y_ba = 0,4

Тогда коэффициент ширины зуба по диаметру y_bd определяем по формуле:

y_bd = 0,5×y_ba×(u+1) = 0,5×0,4×(2,5+1) = 0,7.

2. Проектный расчет заключается в определении межосевого расстояния проектируемой передачи:

,

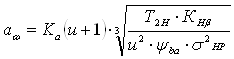где K_a = 495 – вспомогательный коэффициент, зависящий от вида передачи и материала зубчатых колёс (т.к. прямозубая передача.);

T₂_H = 175,901– вращающий момент на валу колеса, Н×м;

u = 2,5– передаточное отношение;

K_H_b = 1,07–коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий, зависит от параметра y_bd, схемы передачи и твердости активных поверхностей зубьев;

y_ba = 0,4– коэффициент ширины зуба;

σ_HP – допускаемое контактное напряжение, МПа.

Допускаемые контактные σ_HP напряжения определяют раздельно для шестерни и колеса по формуле:

,

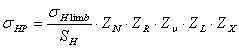где σ_Hlimb_1,2 =2×Н_HB+70 МПа– предел контактной выносливости, соответствующий базовому числу циклов напряжений, для закалённых колес.

σ_Hlimb₁ = 2×Н_НВ + 70=2×265+70=600 МПа

σ_Hlimb₂ = 2×Н_НВ + 70=2×200+70=570 МПа

S_H_1,2 = 1,1– коэффициент запаса прочности (т.к улучшение);

Z_R – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев;

Z_u – коэффициент, учитывающий окружную скорость;

Z_L – коэффициент, учитывающий влияние вязкости масла;

Z_X – коэффициент, учитывающий размер зубчатого колеса.

В проектировочном расчете

Z_R ×Z_u ×Z_L ×Z_X = 0,9.

Тогда:

Z_N – коэффициент долговечности;

Суммарное число циклов перемены напряжений N_К при постоянной нагрузке определяется следующим образом:

N_K = 60×c×n×t,

где с – число зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом, n – частота вращения, рассчитываемого зубчатого колеса (шестерни), об/мин, t = 22000– срок службы передачи, в часах.

Таким образом:

N_K₁ = 60×c×n₁×t = 60∙1∙285∙25000 = 428∙10⁶ циклов,

N_K₂ = 60×c×n₂×t = 60∙1∙114∙25000 = 171∙10⁶ циклов.

Базовые числа циклов напряжений, соответствующие пределу выносливости, определяется по формуле:

N_Hlim_1,2 = 30×H_HB₁^2,4_,

N_Hlim₁ = 30∙265^2,4= 20∙10⁶

N_Hlim₂ = 30∙250^2,4= 17∙10⁶

Так как N_K > N_Hlim определяем значение Z_N по формуле:

Z_N₁ = 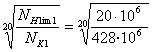= 0,858,

Так как N_K < N_Hlim определяем значение Z_N по формуле:

Z_N₁ = 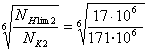= 0,891.

Принимаем Z_N₁= Z_N₂ = 0,9 (соответственно графику).

Используя полученные данные, найдем допускаемые контактные напряжения σ_HP, МПа:

∙0,9∙0,9 = 442,

∙0,9∙0,9 = 420.

В качестве допускаемого контактного напряжения σ_HP для прямозубой передачи при проектировочном расчете принимают допускаемое напряжение того зубчатого колеса (шестерни или колеса), для которого оно меньше, то есть:

σ_HP = σ_HP₂=420 МПа.

Полученные данные подставим в формулу по определению межосевого расстояния:

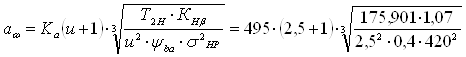=130,497 мм.

Полученное межосевое расстояние округляется до стандартного значения: a_ω = 125 мм.

3. Рассчитываем значение модуля:

m = (0,01…0,02)×a_ω = (0,01…0,02)×125=1,25…2,5 мм.

По ГОСТ 9563-80 принимаем стандартный нормальный модуль:

m = 2,5 мм.

4. Угол наклона зубьев b = 0°

Определяем суммарное число зубьев z_C шестерни z₁ и колеса z₂:

z_C= (2×a_ω×сosb)/m = 2∙125∙сos(0°)/2,5 = 100,

Тогда:

z₁= z_C/(1+u) = 100/(2,5+1) = 29,

z₂= z_С– z₁ = 100 – 29= 71.

где z_min = 17 для передач без смещения.

5. Уточняем передаточное число и его погрешность по формулам:

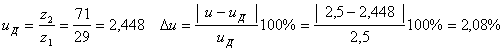что меньше допустимых максимальных 3%.

6. Уточняем значение угла b по формуле:

, тогда b = 0°

7. Основные размеры шестерни и колеса:

7.1 Делительные диаметры шестерни и колеса определяются по формуле, мм:

7.2 Диаметры вершин зубьев определяются по формуле с учетом того, что зубья изготовлены без смещения (х = 0), мм:

d_a1 = d₁ + 2×m= 72,5 + 2×2,5=77,5,

d_a2 = d₂ + 2×m = 177,5 + 2,5×2= 182,5;

7.3 Диаметры впадин, мм:

d_f₁=d₁– 2,5×m = 72,5 – 2,5×2,5 = 66,25,

d_f₂=d₂– 2,5×m = 177,5 – 2,5×2,5 = 171,25;

7.4 Основные диаметры, мм:

d_b1 = d₁∙cosa_t = 72,5×cos20 = 68,128,

d_b2 = d₂∙cosa_t = 177,5×cos20 = 166,795,

где делительный угол профиля в торцовом сечении:

°.

Проверим полученные диаметры по формуле:

a_ω= (d₁+ d₂)/2 = (72,5+ 177,5)/2 = 125,

что совпадает с ранее найденным значением.

7.5 Ширина колеса определяется по формуле:

b₂ = y_ba×a_ω = 0,4∙125 = 50мм.

7.6 Ширина шестерни определяется по формуле:

b₁ = b₂ + (5...10) = 50 + (5...10) = 55…60 мм.

Полученное значение ширины округляем до нормального линейного размера: b₁ = 57 мм.

9. Определим окружную скорость зубчатых колес по формуле:

м/c.

По окружной скорости колес назначаем 9-ю степень точности зубчатых колес.

11. Проверочный расчет на контактную выносливость активных поверхностей зубьев

11.1 Определение расчетного контактного напряжения

Контактная выносливость устанавливается сопоставлением, действующим в полосе зацепления расчетного и допускаемого контактного напряжений:

σ_H = σ_H₀×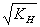≤ σ_HP,

где K_H – коэффициент нагрузки;

σ_H₀– контактное напряжение в полюсе зацепления при K_H = 1.

Контактное напряжение в полюсе зацепления при K_H = 1 определяют следующим образом, МПа:

σ_H₀ = Z_E×Z_H×Z_e,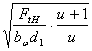

где Z_E = 190– коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес, для стальных зубчатых колес;

Z_H – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления определяется по формуле:

где делительный угол профиля в торцовом сечении:

°;

основной угол наклона:

β_b = arcsin(sinβ×cos20°) = arcsin(0×0,94) = 0°;

угол зацепления:

так как х₁ + х₂ = 0, то a_t_w = a_t = 20°.

Коэффициент осевого перекрытия e_bопределяется по формуле:

e_b= b_w/ p_X,

где осевой шаг:

Z_e – коэффициент, учитывающий суммарную длину контактных линий определяется по формуле:

, так как e_b=0

где коэффициент торцового перекрытия: e_a =e_а1 + e_а2,

составляющие коэффициента торцового перекрытия:

где углы профиля зуба в точках на окружностях вершин:

тогда e_a =e_а1 + e_а2= 0,823 + 0,905 = 1,728.

F_tH = 2000×T₁_H/d₁ = 2000×72,157/72,5 = 1990,538– окружная сила на делительном цилиндре, Н;

b_ω = b₂ = 50– рабочая ширина венца зубчатой передачи мм;

d₁ = 72,5– делительный диаметр шестерни мм,

Подставив полученные данные в формулу, получим:

σ_H₀ = Z_E×Z_H×Z_e361,609.

Коэффициент нагрузки K_H определяют по зависимости:

K_H = K_А×K_H_a×K_Hβ×K_H_u,

где K_А= 1– коэффициент, учитывающий внешнюю динамическую нагрузку;

K_H_a = 1 (так как прямозубая передача)– коэффициент, учитывающий распределение нагрузки между зубьями, зависит от окружной скорости и степени точности по нормам плавности;

K_Hβ = 1,07– коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба зависит от параметра y_bd, схемы передачи и твердости активных поверхностей зубьев;

K_H_u – коэффициент, учитывающий динамическую нагрузку определяется по формуле:

K_H_u= 1 + ω_H_u×b_ω /(F_tH×K_A) = 1 + 3,348×50 /(1990,538×1) = 1,084,

Где

= 3,348,

где w_H_u – удельная окружная динамическая сила, Н/мм;

u = 1,081м/с – окружная скорость на делительном цилиндре;

d_Н = 0,06 – коэффициент, учитывающий влияние зубчатой передачи и модификации профиля головок зубьев (т.к. зубья прямые);

g₀ = 7,3 – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса .

Таким образом:

K_H = K_A∙K_H_u∙K_H_b∙K_H_a = 1×1×1,07×1,084 = 1,1599

Тогда:

σ_H = σ_H₀×= 361,609∙ = 389,448 МПа.

11.2 Допускаемые контактные напряжения в проверочном расчете

Допускаемые контактные напряжения σ_H_Р определяют раздельно для шестерни и колеса, МПа:

σ_H_Р =×Z_R×Z_u×Z_L×Z_X×,

где σ_Hlimb– предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов напряжении;

s_Hlimb₁= 600 МПа, s_Hlimb₂= 570 МПа – рассчитаны ранее;

S_H = 1,1 – минимальный коэффициент запаса прочности (для однородной структуры);

Z_N_1,2 =0,9 – коэффициент долговечности (определены в проектировочном расчете);

Z_L= 1– коэффициент, учитывающий влияние вязкости смазочного материала (т.к. отсутствуют экспериментальные данные);

Z_R= 1 – коэффициент, учитывающий влияние исходной шероховатости сопряженных поверхностей зубьев (т.к. отсутствуют экспериментальные данные);

Z_u = 1– коэффициент, учитывающий влияние окружной скорости (т.к. скорость < 5 м/с);

Z_X_1,2 = 1 – коэффициент, учитывающий размер зубчатого колеса поскольку d₁ < 700 и d₂ < 700

Тогда допускаемые контактные напряжения, МПа:

В качестве допускаемого контактного напряжения передачи, которое сопоставляют с расчетным, принимают:

s_HP = s_HP₂=s_НР_min =438,615

Сопоставим расчетное и допускаемое контактные напряжения:

σ_H ≤ σ_HP,

389,448 ≤ 438,615 – условие выполнено.

недогруз = , что меньше максимально допустимых 20%.

12. Проверочный расчет на контактную выносливость при действии максимальной нагрузки

Действительное напряжение s_Hmax определяют по формуле:

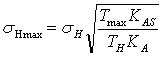≤s_HPmax

где К_AS = 3 – коэффициент внешней динамической нагрузки при расчетах на прочность от максимальной нагрузки;

К_A = 1 – коэффициент, учитывающий внешнюю динамическую нагрузку, (определен ранее);

Т_мах / T_H = К_пер = 1,45(исходные данные).

Таким образом:

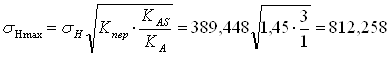МПа.

Допускаемое контактное напряжение при максимальной нагрузке, не вызывающее остаточных деформаций или хрупкого разрушения поверхностного слоя s_HPmax, зависит от способа химико-термической обработки зубчатого колеса и от характера изменения твердости по глубине зуба. Для зубьев, подвергнутых улучшению, принимают:

s_HPmax_1,2= 2,8s_Т

тогда s_HPmax₁= 28·690 =1932 МПа, s_HPmax₂= 28·540 =1512 МПа.

Проверка условия прочности:

s_Hmax≤ s_HPmax₁→ 812,258 МПа ≤ 1932 МПа – условие выполнено;

s_Hmax≤ s_HPmax₂→ 812,258 МПа ≤ 1512 МПа – условие выполнено.

13. Расчет зубьев на выносливость при изгибе

13.1 Определение расчетного изгибного напряжения

Расчетом определяют напряжение в опасном сечении на переходной поверхности зуба для каждого зубчатого колеса.

Выносливость зубьев, необходимая для предотвращения усталостного излома зубьев, устанавливают сопоставлением расчетного местного напряжения от изгиба в опасном сечении на переходной поверхности и допускаемого напряжения:

s_F £ s_FP.

Расчетное местное напряжение при изгибе определяют по формуле, МПа:

s_F = ×K_F×Y_FS×Y_β×Y_ε

где F_tF =1990,538– окружная сила на делительном цилиндре, Н;

b_ω = 50– рабочая ширина венца зубчатой передачи, мм;

m = 2,5– нормальный модуль, мм;

Y_FS– коэффициент, учитывающий форму зуба и концентрацию напряжений определяется по формуле:

где x₁ = x₂ = 0 – коэффициенты смещения;

z_u₁ = z₁ / cos³β = 29/1³ = 29 – эквивалентное число зубьев шестерни,

z_u₂ = z₂ / cos³β = 71/1³ = 71 – эквивалентное число зубьев колеса.

Тогда:

Y_β = 1(т.к. β = 0)– коэффициент, учитывающий наклон зуба;

Y_ε =1(т.к. передача прямозубая) – коэффициент, учитывающий перекрытие зубьев;

K_F– коэффициент нагрузки принимают по формуле:

K_F = K_A×K_F_u×K_F_b×K_F_a,

где K_A = 1– коэффициент, учитывающий внешнюю динамическую нагрузку (не учтенную в циклограмме нагружения);

K_F_u= 1,225– коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса определяется по таблице.

K_F_b = 1,07 – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий (по графику);

K_F_a = 1(т.к. прямозубая передача)– коэффициент, учитывающий распределение нагрузки между зубьями;

Таким образом:

K_F = K_A×K_F_u×K_F_b×K_F_a = 1×1,225×1,07×1 = 1,311.

Тогда:

s_F1 = ×K_F×Y_FS1×Y_β×Y_ε= ×1,311×3,925×1∙1 = 81,941 МПа,

s_F2 = ×K_F×Y_FS2×Y_β×Y_ε= ×1,311×3,656×1∙1 = 76,325 МПа.

13.2 Допускаемые напряжения в проверочном расчете на изгиб

Допускаемым напряжением s_FP определяются по формуле:

s_FP = 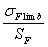×Y_N×Y_δ×Y_R×Y_X,

где s_Flimb – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа определяется по формуле:

s_Flimb =s⁰_Flimb×Y_T×Y_z×Y_g×Y_d×Y_A ,

где s⁰_Flimb – предел выносливости при отнулевом цикле изгиба,

для колес из стали марки 40Х, подвергшейся улучшению s⁰_Flimb = 1,75Н_НВ МПа.

s⁰_Flimb₁ = 1,75*265 = 463,75 МПа. s⁰_Flimb₂ = 1,75*250=437,5 МПа.

Y_T принимают Y_T₁ = Y_T₂ = 1, поскольку в технологии изготовления шестерни и колеса нет отступлений от примечаний к соответствующим табл. – коэффициент, учитывающий технологию изготовления;

Y_z – коэффициент, учитывающий способ получения заготовки зубчатого колеса для поковки Y_z₁ = 1 и Y_z₂ = 1;

Y_g– коэффициент, учитывающий влияние шлифования передней поверхности зуба Y_g₁ = Y_g₂ = 1, так как шлифование не используется;

Y_d – коэффициент, учитывающий влияние деформационного упрочнения или электрохимической обработки переходной поверхности, Y_d₁ = Y_d₂ = 1, так как отсутствует деформационное упрочнение;

Y_A = 1– коэффициент, учитывающий влияние двустороннего приложения нагрузки так как одностороннее приложение нагрузки.

Тогда:

s_Flimb1 =s⁰_Flimb1×Y_T×Y_z×Y_g×Y_d×Y_A= 463,75×1×1×1×1×1 = 463,75 МПа;

s_Flimb₂ =s⁰_Flimb₂×Y_T×Y_z×Y_g×Y_d×Y_A= 437,5×1×1×1×1×1 = 437,5 МПа.

S_F = 1,7 – коэффициент запаса прочности определяется в зависимости от способа термической и химико-термической обработки;

Y_N – коэффициент долговечности находится по формуле:

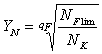но не менее 1,

где q_F – показатель степени;

N_Flim – базовое число циклов перемены напряжений, N_Flim= 4×10⁶ циклов;

N_К – суммарное число циклов перемены напряжений, уже определены:

N_K₁ = 427,5∙10⁶ циклов,

N_K₂ = 171∙10⁶ циклов.

Так как N_K₁ > N_Flim = 4×10⁶и N_K₂ > N_Flim, то Y_N₁= Y_N2 =1.

Y_δ – коэффициент, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений находится в зависимости от значения модуля m по формуле:

Y_δ = 1,082 – 0,172∙lgm = 1,082 – 0,172∙lg2,5 = 1,014

Y_R – коэффициент, учитывающий шероховатость переходной поверхности: при улучшении Y_R_1,2 = 1,2.

Y_X – коэффициент, учитывающий размеры зубчатого колеса определяется по формуле:

Y_X₁ = 1,05 – 0,000125∙d₁ = 1,05 – 0,000125×72,5 = 1,041,

Y_X₂ = 1,05 – 0,000125∙d₂ = 1,05 – 0,000125×177,5 = 1,028

Таким образом:

МПа,

МПа.

Сопоставим расчетные и допускаемые напряжения на изгиб:

s_F₁= 80,941 < s_FP₁ = 345,545,

s_F₂ =76,325 < s_FP₂ = 321,915.

Условие выполняется.

13.3 Расчет на прочность при изгибе максимальной нагрузкой

Прочность зубьев, необходимая для предотвращения остаточных деформаций, хрупкого излома или образования первичных трещин в поверхностном слое, определяют сопоставлением расчетного (максимального местного) и допускаемого напряжений изгиба в опасном сечении при действии максимальной нагрузки:

s_Fmax£ s_FPmax.

Расчетное местное напряжение s_Fmax, определяют по формуле:

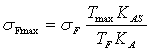где К_AS = 3– коэффициент внешней динамической нагрузки при расчетах на прочность от максимальной нагрузки;

К_A = 1 – коэффициент, учитывающий внешнюю динамическую нагрузку, (определен ранее);

Т_мах / T_F = К_пер = 1,45(исходные данные).

Таким образом:

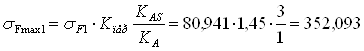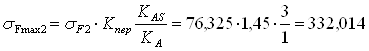МПа,

МПа.

Допускаемое напряжение s_FPmax определяют раздельно для зубчатых колес (шестерни и колеса) по формуле:

где σ_FSt – предельное напряжение зубьев при изгибе максимальной нагрузкой, МПа; определяем по приближённой зависимости:

σ_FSt ≈ σ_Flimb×Y_Nmax×K_St

где σ_Flimb – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа;

σ_Flimb₁ = 463,75 МПа σ_Flimb₂ = 437,5 МПа

Y_Nmax_1,2 = 4 (т.к. q_F = 6)– коэффициент, учитывающий влияние деформационного упрочнения.

K_St_1,2 = 1,3 (т.к. q_F = 6)– коэффициент, учитывающий различие между предельными напряжениями, определёнными при ударном, однократном нагружении и при числе ударных нагружений N = 10³;

Тогда:

σ_FSt1 ≈ σ_Flim1×Y_Nmax1×K_St1 = 463,75∙4∙1,3 = 2411,5 МПа,

σ_FSt₂ ≈ σ_Flimb₂×Y_Nmax₂×K_St₂ = 437,5×4×1,3 = 2275 МПа.

S_FSt = 1,75 – коэффициент запаса прочности;

Y_X – коэффициент учитывающий размер зубчатого колеса, определяется по формуле. Y_X₁ = 1,041, Y_X₂ = 1,028 (определены ранее).

коэффициент Y_RSt= 1 и отношение Y_d_St/Y_d_StT = 1.

Получим:

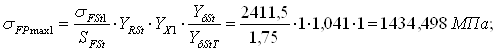
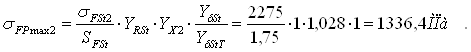
Проверка условия прочности:

s_Fmax₁≤ s_FPmax₁→ 352,093МПа ≤ 1434,498 МПа – условие выполнено;

s_Fmax₂≤ s_FPmax₂→ 332,014 МПа ≤ 1336,4 МПа – условие выполнено.

Расчет цилиндрической передачи

Расчет косозубой быстроходной ступени.

Исходные данные:

Выбираем материалы для изготовления зубчатых колёс и способы из термообработки:

Выбираем в зависимости от выходной мощности

Так как

N_ВЫХ =кВт,

тогда материалы зубчатых колес – Сталь 40Х.

Термообработка:

шестерни – улучшение, твердость Н₁ = Н₂ (269…262)=265НВ;

колеса – улучшение, твердость Н₂ = (235…262)=250НВ.

u = 2,5 – передаточное число.

n₁ = 712,5об/мин – частота вращения шестерни,

n₂ = 285об/мин – частота вращения колеса,

T₁ = 29,6 Н∙м – вращающий момент на шестерне,

T₂ = 72,157Н∙м – вращающий момент на колесе,

Коэффициент перегрузки при пуске двигателя К_пер = 1,45.

1. Выбираем коэффициент ширины зуба y_ba с учетом того, что имеем несимметричное расположение колес относительно опор: y_ba = 0,315

Тогда коэффициент ширины зуба по диаметру y_bd определяем по формуле:

y_bd = 0,5×y_ba×(u+1) = 0,5×0,315×(2,5+1) = 0,55.

2. Проектный расчет заключается в определении межосевого расстояния проектируемой передачи:

,

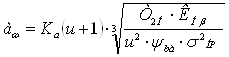ак, как редуктор соосный, следовательно принимаем межосевое расстояние равное межосевому расстоянию тихоходной ступени (прямозубой передачи), тогда 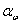= 125 мм.

3. Рассчитываем значение модуля:

m = (0,01…0,02)×a_ω = (0,01…0,02)×125 = 1,25…2,5 мм.

По ГОСТ 9563-80 принимаем стандартный нормальный модуль:

m = 2,5 мм.

4. Задаёмся углом наклона b = 16° и определяем суммарное z_C число зубьев шестерни z₁ и колеса z₂:

z_C= (2×a_ω×сosb)/m = 2∙125∙сos(13°)/2,5 = 97,43,

Полученное значение округляем до целого числа: z_C = 97.

Тогда:

z₁= z_C/(1+u) = 97/(2,5+1) = 27,714,

z₂= z_С– z₁ = 97 – 28 = 69.

где z_min = 17 для передач без смещения.

5. Уточняем передаточное число и его погрешность по формулам:

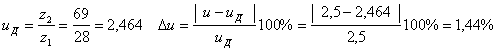что меньше допустимых максимальных 3%.

6. Уточняем значение угла b по формуле:

, тогда b = 14°04’12”

7. Основные размеры шестерни и колеса:

7.1 Делительные диаметры шестерни и колеса определяются по формуле, мм:

7.3 Диаметры вершин зубьев определяются по формуле с учетом того, что зубья изготовлены без смещения (х = 0), мм:

d_a1 = d₁ + 2×m= 72,165 + 2×2,5 = 77,165,

d_a2 = d₂ + 2×m = 177,835 + 2×2,5 = 182,835;

7.6 Диаметры впадин, мм:

d_f₁=d₁– 2,5×m = 72,165 – 2,5×2,5 = 66,915,

d_f₂=d₂– 2,5×m = 177,835– 2,5×2,5 = 171,585;

7.7 Основные диаметры, мм:

d_b1 = d₁∙cosa_t = 72,165×0,936 = 67,564,

d_b2 = d₂∙cosa_t = 177,835×0,936 = 166,497,

где делительный угол профиля в торцовом сечении:

°.

Проектирование электродвигателя

ЭД – электродвигатель

Энерго-кинематический расчет привода

Исходные данные для расчета:

Выбор параметров передач и элементов привода

Сводная таблица вращающих моментов и частот вращения валов привода:

2. Проектный расчет заключается в определении межосевого расстояния проектируемой передачи:

,

где Ka = 495 – вспомогательный коэффициент, зависящий от вида передачи и материала зубчатых колёс (т.к. прямозубая передача.);

T2H = 175,901– вращающий момент на валу колеса, Н×м;

u = 2,5– передаточное отношение;

yba = 0,4– коэффициент ширины зуба;

Допускаемые контактные σHP напряжения определяют раздельно для шестерни и колеса по формуле:

,

где σHlimb1,2 =2×НHB+70 МПа– предел контактной выносливости, соответствующий базовому числу циклов напряжений, для закалённых колес.

σHlimb1 = 2×ННВ + 70=2×265+70=600 МПа

σHlimb2 = 2×ННВ + 70=2×200+70=570 МПа

SH1,2 = 1,1– коэффициент запаса прочности (т.к улучшение);

ZR – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев;

Zu – коэффициент, учитывающий окружную скорость;

ZL – коэффициент, учитывающий влияние вязкости масла;

ZX – коэффициент, учитывающий размер зубчатого колеса.

ZN – коэффициент долговечности;

σHP = σHP2=420 МПа.

Полученные данные подставим в формулу по определению межосевого расстояния:

=130,497 мм.

Полученное межосевое расстояние округляется до стандартного значения: aω = 125 мм.

3. Рассчитываем значение модуля:

По ГОСТ 9563-80 принимаем стандартный нормальный модуль:

m = 2,5 мм.

4. Угол наклона зубьев b = 0°

Определяем суммарное число зубьев zC шестерни z1 и колеса z2 :

zC= (2×aω×сosb)/m = 2∙125∙сos(0°)/2,5 = 100,

Тогда:

z1 = zC/(1+u) = 100/(2,5+1) = 29,

z2 = zС – z1 = 100 – 29= 71.

где zmin = 17 для передач без смещения.

5. Уточняем передаточное число и его погрешность по формулам:

6. Уточняем значение угла b по формуле:

7. Основные размеры шестерни и колеса:

7.1 Делительные диаметры шестерни и колеса определяются по формуле, мм:

7.2 Диаметры вершин зубьев определяются по формуле с учетом того, что зубья изготовлены без смещения (х = 0), мм:

da1 = d1 + 2×m= 72,5 + 2×2,5=77,5,

da2 = d2 + 2×m = 177,5 + 2,5×2= 182,5;

7.3 Диаметры впадин, мм:

df1=d1 – 2,5×m = 72,5 – 2,5×2,5 = 66,25,

df2=d2 – 2,5×m = 177,5 – 2,5×2,5 = 171,25;

7.4 Основные диаметры, мм:

db2 = d2∙cosat = 177,5×cos20 = 166,795,

Проверим полученные диаметры по формуле:

aω= (d1 + d2)/2 = (72,5+ 177,5)/2 = 125,

что совпадает с ранее найденным значением.

7.5 Ширина колеса определяется по формуле:

7.6 Ширина шестерни определяется по формуле:

Полученное значение ширины округляем до нормального линейного размера: b1 = 57 мм.

9. Определим окружную скорость зубчатых колес по формуле:

11.1 Определение расчетного контактного напряжения

Контактная выносливость устанавливается сопоставлением, действующим в полосе зацепления расчетного и допускаемого контактного напряжений:

σH = σH0×≤ σHP,

где KH – коэффициент нагрузки;

σH0 – контактное напряжение в полюсе зацепления при KH = 1.

Контактное напряжение в полюсе зацепления при KH = 1 определяют следующим образом, МПа:

σH0 = ZE×ZH×Ze,

где ZE = 190– коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес, для стальных зубчатых колес;

ZH – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления определяется по формуле:

Коэффициент осевого перекрытия ebопределяется по формуле:

eb= bw/ pX,

Ze – коэффициент, учитывающий суммарную длину контактных линий определяется по формуле:

FtH = 2000×T1H/d1 = 2000×72,157/72,5 = 1990,538– окружная сила на делительном цилиндре, Н;

bω = b2 = 50– рабочая ширина венца зубчатой передачи мм;

d1 = 72,5– делительный диаметр шестерни мм,

Коэффициент нагрузки KH определяют по зависимости:

KH = KА×KHa×KHβ×KHu,

где KА = 1– коэффициент, учитывающий внешнюю динамическую нагрузку;

KHu – коэффициент, учитывающий динамическую нагрузку определяется по формуле:

11.2 Допускаемые контактные напряжения в проверочном расчете

Допускаемые контактные напряжения σHР определяют раздельно для шестерни и колеса, МПа:

σHР =×ZR×Zu×ZL×ZX×,

ZX1,2 = 1 – коэффициент, учитывающий размер зубчатого колеса поскольку d1 < 700 и d2 < 700

Yβ = 1(т.к. β = 0)– коэффициент, учитывающий наклон зуба;

где K_a = 495 – вспомогательный коэффициент, зависящий от вида передачи и материала зубчатых колёс (т.к. прямозубая передача.);

T₂_H = 175,901– вращающий момент на валу колеса, Н×м;

y_ba = 0,4– коэффициент ширины зуба;

Допускаемые контактные σ_HP напряжения определяют раздельно для шестерни и колеса по формуле:

где σ_Hlimb_1,2 =2×Н_HB+70 МПа– предел контактной выносливости, соответствующий базовому числу циклов напряжений, для закалённых колес.

σ_Hlimb₁ = 2×Н_НВ + 70=2×265+70=600 МПа

σ_Hlimb₂ = 2×Н_НВ + 70=2×200+70=570 МПа

S_H_1,2 = 1,1– коэффициент запаса прочности (т.к улучшение);

Z_R – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев;

Z_u – коэффициент, учитывающий окружную скорость;

Z_L – коэффициент, учитывающий влияние вязкости масла;

Z_X – коэффициент, учитывающий размер зубчатого колеса.

Z_N – коэффициент долговечности;

σ_HP = σ_HP₂=420 МПа.

Полученное межосевое расстояние округляется до стандартного значения: a_ω = 125 мм.

Определяем суммарное число зубьев z_C шестерни z₁ и колеса z₂:

z_C= (2×a_ω×сosb)/m = 2∙125∙сos(0°)/2,5 = 100,

z₁= z_C/(1+u) = 100/(2,5+1) = 29,

z₂= z_С– z₁ = 100 – 29= 71.

где z_min = 17 для передач без смещения.

d_a1 = d₁ + 2×m= 72,5 + 2×2,5=77,5,

d_a2 = d₂ + 2×m = 177,5 + 2,5×2= 182,5;

d_f₁=d₁– 2,5×m = 72,5 – 2,5×2,5 = 66,25,

d_f₂=d₂– 2,5×m = 177,5 – 2,5×2,5 = 171,25;

d_b2 = d₂∙cosa_t = 177,5×cos20 = 166,795,

a_ω= (d₁+ d₂)/2 = (72,5+ 177,5)/2 = 125,

Полученное значение ширины округляем до нормального линейного размера: b₁ = 57 мм.

σ_H = σ_H₀×≤ σ_HP,

где K_H – коэффициент нагрузки;

σ_H₀– контактное напряжение в полюсе зацепления при K_H = 1.

Контактное напряжение в полюсе зацепления при K_H = 1 определяют следующим образом, МПа:

σ_H₀ = Z_E×Z_H×Z_e,

где Z_E = 190– коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес, для стальных зубчатых колес;

Z_H – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления определяется по формуле:

Коэффициент осевого перекрытия e_bопределяется по формуле:

e_b= b_w/ p_X,

Z_e – коэффициент, учитывающий суммарную длину контактных линий определяется по формуле:

F_tH = 2000×T₁_H/d₁ = 2000×72,157/72,5 = 1990,538– окружная сила на делительном цилиндре, Н;

b_ω = b₂ = 50– рабочая ширина венца зубчатой передачи мм;

d₁ = 72,5– делительный диаметр шестерни мм,

Коэффициент нагрузки K_H определяют по зависимости:

K_H = K_А×K_H_a×K_Hβ×K_H_u,

где K_А= 1– коэффициент, учитывающий внешнюю динамическую нагрузку;

K_H_u – коэффициент, учитывающий динамическую нагрузку определяется по формуле:

Допускаемые контактные напряжения σ_H_Р определяют раздельно для шестерни и колеса, МПа:

σ_H_Р =×Z_R×Z_u×Z_L×Z_X×,

Z_X_1,2 = 1 – коэффициент, учитывающий размер зубчатого колеса поскольку d₁ < 700 и d₂ < 700

Y_β = 1(т.к. β = 0)– коэффициент, учитывающий наклон зуба;

K_F = K_A×K_F_u×K_F_b×K_F_a,

где K_A = 1– коэффициент, учитывающий внешнюю динамическую нагрузку (не учтенную в циклограмме нагружения);

K_F_u= 1,225– коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса определяется по таблице.

K_F_b = 1,07 – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий (по графику);

K_F_a = 1(т.к. прямозубая передача)– коэффициент, учитывающий распределение нагрузки между зубьями;

Допускаемым напряжением s_FP определяются по формуле:

s_FP = ×Y_N×Y_δ×Y_R×Y_X,

где s_Flimb – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа определяется по формуле:

s_Flimb =s⁰_Flimb×Y_T×Y_z×Y_g×Y_d×Y_A ,

где s⁰_Flimb – предел выносливости при отнулевом цикле изгиба,

Y_z – коэффициент, учитывающий способ получения заготовки зубчатого колеса для поковки Y_z₁ = 1 и Y_z₂ = 1;

Y_g– коэффициент, учитывающий влияние шлифования передней поверхности зуба Y_g₁ = Y_g₂ = 1, так как шлифование не используется;

4. Задаёмся углом наклона b = 16° и определяем суммарное z_C число зубьев шестерни z₁ и колеса z₂:

z_C= (2×a_ω×сosb)/m = 2∙125∙сos(13°)/2,5 = 97,43,

Полученное значение округляем до целого числа: z_C = 97.

z₁= z_C/(1+u) = 97/(2,5+1) = 27,714,

z₂= z_С– z₁ = 97 – 28 = 69.

где z_min = 17 для передач без смещения.

d_a1 = d₁ + 2×m= 72,165 + 2×2,5 = 77,165,

d_a2 = d₂ + 2×m = 177,835 + 2×2,5 = 182,835;

d_f₁=d₁– 2,5×m = 72,165 – 2,5×2,5 = 66,915,

d_f₂=d₂– 2,5×m = 177,835– 2,5×2,5 = 171,585;

d_b2 = d₂∙cosa_t = 177,835×0,936 = 166,497,

a_ω= (d₁+ d₂)/2 = (72,165+ 177,835)/2 = 125 мм,