Разработка печатного модуля РЭС с использованием учебных алгоритмов САПР

1. Решение задачи компоновки для функциональной схемы с использованием последовательного алгоритма

1.1 Общее описание алгоритма

1.2 Пошаговое описание алгоритма

1.3 Выполнение компоновки

2. Размещение элементов в принципиальной электрической схеме с использованием последовательного алгоритма

2.1 Краткое описание алгоритма последовательной установки элементов РЭА

2.2 Выполнение размещения

2.3 Результаты размещения

3. Трассировка цепей питания и земли с использованием алгоритма построения кратчайших связывающих сетей и волнового алгоритма

3.1 Краткое описание алгоритма Краскала

3.2 Трассировка цепей земли по алгоритму Краскала

3.3 Трассировка цепей питания по алгоритму Прима

4. Трассировка сигнальных цепей с помощью волновых алгоритмов

Заключение

Список используемой литературы

Введение

Стремление разработать эффективные методы конструирования РЭА, позволяющие обобщить опыт работы высоко квалифицированных конструкторов и сделать их достаточно универсальными, приводит к необходимости формализации процесса конструирования.

Разработанная обобщённая модель конструкции РЭА подвергается тщательным исследованиям с точки зрения удовлетворения параметров конструкций заданным техническим требованиям.

Успешное решение формализации конструкторской деятельности возможно лишь только при её алгоритмизации и автоматизации с использованием математических методов, теории графов, алгоритмов, математического программирования и исследование операции, методов вычислительной математики.

Следует отметить, что в общем случае процессы конструирования РЭА плохо поддаются формализации и с математической точки зрения относятся к так называемым плохо формализуемым задачам. Тем не менее для широкого круга задач удалось найти математическое описание и на его основе построить алгоритмы и программы их решения на ЭВМ.

В настоящее время на основе современных вычислительных комплексов и средств автоматизации созданы и находятся в промышленной эксплуатации схемы автоматизированного проектирования РЭА и ЭВА, позволяющие в значительной степени освободить конструктора-проектировщика от однообразной, трудоёмкой и утомительной умственной работы и повысить его интеллектуальные возможности на этапах принятия решений.

Существующие системы автоматизированного проектирования РЭА решают комплекс вопросов по проектированию схем и конструкций аппаратуры.

Нам необходимо разработать печатный модуль РЭС с использованием учебных алгоритмов САПР.

1. Решение задачи компоновки

1.1 Общее описание алгоритма

Общая схема процесса последовательной компоновки по связности имеет следующий вид:

Пусть дана схема соединения элементов из множества . Определим последовательный процесс назначения элементов  в узлы Br(), на каждом шаге которого выбирается один из неразделенных элементов и приписывается очередному узлу.

Узел считается завершенным, если число элементов в узле равно заданному числу K.

После завершения очередного узла аналогичная процедура повторяется для следующего узла, причем кандидатами для назначения являются элементы, не включенные в предыдущие узлы. Процесс заканчивается, когда все элементы из множества E распределены.

Исходные данные являются:

– электрическая схема устройства (Рис.1);

– максимально допустимое число элементов в модуле.

Электрическую схему удобно представлять графом G=(E,V), где множество вершин Е соответствует элементам электрической схемы, а множество ребер V –электрическим связям между элементами.

В таком виде задача компоновки может быть сформулирована как задача разрезания графа

G=(E,V) на множество подграфов

Gr = (Er, Vr),

где r=1, 2, 3….

В каждом подграфе число вершин соответственно Er должно не превосходить ранее заданного ограничения на число элементовв в узле К. Для любого разбиения должны выполняться следующие условия:

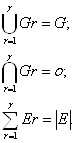 (1)

Рис.1

При проведении компоновки без учета ограничения на кол-во внешних выводов в узле все модули, кроме последнего, будут иметь полное заполнение и последнее условие примет вид

 (2)

1.2 Пошаговое описание алгоритма

Шаг 1.

Формирование очередного подграфа Gr(r=1,2,3…) начинается с выбора базовой вершины  из множества нераспределенных вершин Ir. В начале процесса все вершины считаются нераспределенными, т.е. Ir=E.

Критерием выбора вершины на роль базовой является ее степень () (под степенью вершины графа будем понимать кол-во ребер данного графа, инцидентных ей). Выбор происходит в соответствии со следующим условием:

  (3)

Базовая вершина будет первой по порядку вершиной подграфа Gr(Er,Vr), а оставшиеся вершины, принадлежащие множеству , являются кандидатами для включения в подграф Gr на последующих шагах алгоритма.

Базовая вершина  является, во-первых, как бы “центром” группирования, к которому прибавляются новые вершины, во-вторых, центром факторизации.

Шаг 2.

Из множества  выделяется подмножество Г () вершин, связанных с .

Шаг 3.

Для элемента X введем функционал:

L(x)=  (4)

определяющий число цепей, связывающих вершину X и вершины из множества Г и Ir\.

Для упрощения записей будем отождествлять элемент (множество элементов). Для формального вычисления функционала будем пользоваться формулой:

(5)

где  – число связей между вершинами  и .

Шаг 4.

Из всех вершин  выбирается  такая, у которой значение функционала минимально. Очевидно, что вершина, для которой это условие будет выполняться, максимально связана с . Эта вершина включается во множество Еr вершин Gr.

Множество вершин подграфа Gr приобретает следующий вид:

 (6)

где , а верхний индекс в обозначении  в общем случае указывает кол-во шагов выборки.

Шаг 5.

Происходит стягивание вершин подграфа Gr в вершину . Этот процесс далее будем называть факторизацией, вершину  – центром факторизации, а количество вершин стянутых в , кроме него самого, – степенью факторизации.

Центр факторизации со степенью факторизации , отличной от нуля, будем обозначать символом  и называть гипервершиной степени .

После данного процесса множество  преобразуют в одноэлементное множество  содержащее гипервершину степени .

В указанных обозначениях первый процесс факторизации запишется следующим образом:

. (7)

В общем случае на ом шаге выборки все указанные преобразования будут иметь вид:

. (8)

=1,2,3…,Кс-1,где Кс –допустимая мощность множества вершин формируемого подграфа (кол-во элементов в конструктивном узле).

Шаг 6.

Действия, описанные в шагах 2,3,4,5, повторяются до полного заполнения формируемого модуля.

Далее весь процесс повторяется до тех пор, пока не будет сформирован (-1) модуль. Последний же –й полностью включает в себя множество , так как

. (9)

1.3 Выполнение компоновки

Данную электрическую функциональную схему распределителя уровней на 10 каналов (рис. 1) разбиваем на 3 блока. Далее выполняем компоновку для каждого блока, для чего представляем их в виде графов, где множеству вершин соответствуют элементы электрической схемы блока, а множество ребер электрическим связям между этими элементами.

1.3.1 Компоновка первого блока

В исходной схеме выделяем однотипные логические элементы. Сведём их в блок 1.

Рис. 2. Блок 1

По блоку 1 составляем граф.

Рис. 3. Граф 1

По полученному графу составляем матрицу смежности.

Таблица 1

	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	X11	X12	X13	X14	X15
X1	0	0	0	0	1	1	1	1	0	1	1	0	1	0	1	8
X2	0	0	1	1	0	1	1	1	0	1	1	0	0	1	1	9
X3	0	1	0	1	1	1	0	0	1	0	0	1	1	1	1	9
X4	0	1	1	0	0	0	0	1	1	1	1	0	1	1	0	8
X5	1	0	1	0	0	1	1	0	1	1	1	0	1	1	0	9
X6	1	1	1	0	1	0	1	1	1	0	0	1	0	0	1	9
X7	1	1	0	0	1	1	0	0	0	0	1	1	1	1	0	8
X8	1	1	0	1	0	1	0	0	1	1	0	1	1	1	0	9
X9	0	0	1	1	1	1	0	1	0	1	1	1	0	0	1	9
X10	1	1	0	1	1	0	0	1	1	0	0	0	0	1	1	8
X11	1	1	0	1	1	0	1	0	1	0	0	0	1	0	1	8
X12	0	0	1	0	0	1	1	1	1	0	0	0	1	0	1	7
X13	1	0	1	1	1	0	1	1	0	0	1	1	0	0	0	8
X14	0	1	1	1	1	0	1	1	0	1	0	0	0	0	1	8
X15	1	1	1	0	0	1	0	0	1	1	1	1	0	1	0	9

За базовую принимаем вершину X2, т.к. она имеет максимальное значение, равное 9, и минимальный порядковый номер. Она связана с вершинами X3, X4, X6, X7, X8, X10, X11, X14, X15. Посчитаем для этих вершин функционалы:

L(X1)=8-0=8, L(X3)=9-1=8, L(X4)=8-1=7, L(X5)=9-0=9,

L(X6)=9-1=8, L(X7)=8-1=7, L(X8)=9-1=8, L(X9)=9-0=9, L(X10)=8-1=7, L(X11)=8-1=7, L(X12)=7-0=7, L(X13)=8-0=8, L(X14)=8-1=7, L(X15)=9-1=8.

Стягиваем вершину X4 с базовой в первый корпус, т.к. она имеет минимальный функционал, равный 7, и минимальный порядковый номер.

Таблица 2

	X1	X3	X5	X6	X7	X8	X9	X10	X11	X12	X13	X14	X15
X1	0	0	1	1	1	1	0	1	1	0	1	0	1	0
X3	0	0	1	1	0	0	1	0	0	1	1	1	1	2
X5	1	1	0	1	1	0	1	1	1	0	1	1	0	0
X6	1	1	1	0	1	1	1	0	0	1	0	0	1	1
X7	1	0	1	1	0	0	0	0	1	1	1	1	0	1
X8	1	0	0	1	0	0	1	1	0	1	1	1	0	2
X9	0	1	1	1	0	1	0	1	1	1	0	0	1	1
X10	1	0	1	0	0	1	1	0	0	0	0	1	1	2
X11	1	0	1	0	1	0	1	0	0	0	1	0	1	2
X12	0	1	0	1	1	1	1	0	0	0	1	0	1	0
X13	1	1	1	0	1	1	0	0	1	1	0	0	0	1
X14	0	1	1	0	1	1	0	1	0	0	0	0	1	2
X15	1	1	0	1	0	0	1	1	1	1	0	1	0	1
	0	2	0	1	1	2	1	2	2	0	1	2	1	0

Стягиваем вершину X7 с X4 и с базовой в первый корпус, т.к. вершина X7 также имеет функционал равный 7.

Таблица 3

	X1	X3	X5	X6	X8	X9	X10	X11	X12	X13	X14	X15
X1	0	0	1	1	1	0	1	1	0	1	0	1	1
X3	0	0	1	1	0	1	0	0	1	1	1	1	2
X5	1	1	0	1	0	1	1	1	0	1	1	0	1
X6	1	1	1	0	1	1	0	0	1	0	0	1	2
X8	1	0	0	1	0	1	1	0	1	1	1	0	2
X9	0	1	1	1	1	0	1	1	1	0	0	1	1
X10	1	0	1	0	1	1	0	0	0	0	1	1	2
X11	1	0	1	0	0	1	0	0	0	1	0	1	3
X12	0	1	0	1	1	1	0	0	0	1	0	1	1
X13	1	1	1	0	1	0	0	1	1	0	0	0	2
X14	0	1	1	0	1	0	1	0	0	0	0	1	3
X15	1	1	0	1	0	1	1	1	1	0	1	0	1
	1	2	1	2	2	1	2	3	1	2	3	1	0

Так как К155ЛА4 содержит три модуля, элементы X2, X4, X7 помещаем в одну микросхему. Для оставшихся несвязанных элементов будем продолжать компоновку.

Таблица 4

	X1	X3	X5	X6	X8	X9	X10	X11	X12	X13	X14	X15
X1	0	0	1	1	1	0	1	1	0	1	0	1	7
X3	0	0	1	1	0	1	0	0	1	1	1	1	7
X5	1	1	0	1	0	1	1	1	0	1	1	0	8
X6	1	1	1	0	1	1	0	0	1	0	0	1	7
X8	1	0	0	1	0	1	1	0	1	1	1	0	7
X9	0	1	1	1	1	0	1	1	1	0	0	1	8
X10	1	0	1	0	1	1	0	0	0	0	1	1	6
X11	1	0	1	0	0	1	0	0	0	1	0	1	5
X12	0	1	0	1	1	1	0	0	0	1	0	1	6
X13	1	1	1	0	1	0	0	1	1	0	0	0	6
X14	0	1	1	0	1	0	1	0	0	0	0	1	5
X15	1	1	0	1	0	1	1	1	1	0	1	0	8

За базовую принимаем вершину X5, т.к. она имеет максимальное значение, равное 8, и минимальный порядковый номер. Она связана с вершинами X1, X3, X6, X9, X10, X11, X13, X14. Посчитаем для этих вершин функционалы:

L(X1)=7-1=6, L(X3)=7-1=6, L(X6)=7-1=6, L(X8)=7-0=7, L(X9)=8-1=7, L(X10)=6-1=5, L(X11)=5-1=4, L(X12)=6-0=6, L(X13)=6-1=5, L(X14)=5-1=4, L(X15)=8-0=8.

Стягиваем вершины X11, X14 с базовой во второй корпус, т.к. они имеют минимальный функционал, равный 4.

Таблица 5

	X1	X3	X6	X8	X9	X10	X12	X13	X15
X1	0	0	1	1	0	1	0	1	1	2
X3	0	0	1	0	1	0	1	1	1	2
X6	1	1	0	1	1	0	1	0	1	1
X8	1	0	1	0	1	1	1	1	0	1
X9	0	1	1	1	0	1	1	0	1	2
X10	1	0	0	1	1	0	0	0	1	2
X12	0	1	1	1	1	0	0	1	1	0
X13	1	1	0	1	0	0	1	0	0	2
X15	1	1	1	0	1	1	1	0	0	2
	2	2	1	1	2	2	0	2	2	0

Так как К155ЛА4 содержит три модуля, элементы X5, X11, X14 помещаем в одну микросхему. Для оставшихся несвязанных элементов будем продолжать компоновку.

Таблица 6

	X1	X3	X6	X8	X9	X10	X12	X13	X15
X1	0	0	1	1	0	1	0	1	1	5
X3	0	0	1	0	1	0	1	1	1	5
X6	1	1	0	1	1	0	1	0	1	6
X8	1	0	1	0	1	1	1	1	0	6
X9	0	1	1	1	0	1	1	0	1	6
X10	1	0	0	1	1	0	0	0	1	4
X12	0	1	1	1	1	0	0	1	1	6
X13	1	1	0	1	0	0	1	0	0	4
X15	1	1	1	0	1	1	1	0	0	6

За базовую принимаем вершину X6, т.к. она имеет максимальное значение, равное 6, и минимальный порядковый номер. Она связана с вершинами X1, X3, X8, X9, X12, X15. Посчитаем для этих вершин функционалы:

L(X1)=5-1=4, L(X3)=5-1=4, L(X8)=6-1=5, L(X9)=6-1=5, L(X10)=4-0=4, L(X12)=6-1=5, L(X13)=4-0=4, L(X15)=6-1=5.

Стягиваем вершину X1, X3 с базовой в третий корпус, т.к. они имеют минимальный функционал, равный 4.

Таблица 7

	X8	X9	X10	X12	X13	X15
X8	0	1	1	1	1	0	2
X9	1	0	1	1	0	1	2
X10	1	1	0	0	0	1	1
X12	1	1	0	0	1	1	2
X13	1	0	0	1	0	0	2
X15	0	1	1	1	0	0	3
	2	2	1	2	2	3	0

Так как К155ЛА4 содержит три модуля, элементы X1, X3, X6 помещаем в одну микросхему. Для оставшихся несвязанных элементов будем продолжать компоновку.

Таблица 8

	X8	X9	X10	X12	X13	X15
X8	0	1	1	1	1	0	4
X9	1	0	1	1	0	1	4
X10	1	1	0	0	0	1	3
X12	1	1	0	0	1	1	4
X13