Теория игр

Глава I Основные положения Теории игр

1.1 Предмет и задачи теории игр

1.2 Решение матричной игры в чистых стратегиях

1.3 Решение матричной игры в смешанных стратегиях

1.4 Решение игр графическим методом

1.5 Сведение матричной игры к задаче линейного программирования

1.6 Игры с природой

Выводы по I главе

Глава II Разработка элективного курса “Элементы теории игр в начальной школе”

2.1 Место компьютера в начальной школе

2.3 Игра как метод обучения в начальной школе

2.4 Анализ программ и стандарта по информатике в начальной школе

2.5 Элективный курс

2.6 Педагогический эксперимент

2.7 Описание программного продукта

Выводы по II главе

Заключение

Список использованной литературы

Приложения

Введение

Теория игр была основана Джоном фон Нейманом и Оскаром Моргенштерном в их первой работе "The Theory of Games and Economic Behavior", изданной в 1944 году. В 1928 году в математических анналах фон Нейманом была опубликована статья "О теории общественных игр", в которой впервые было применено понятие "теория игр". Использование этого понятия объясняется схожестью логики принятия решений в таких играх, как шахматы и покер. Характерным для таких ситуаций является то, что результат для принимающего решение зависит не только от его решения, но и от того, какое решение примут другие. Поэтому оптимальный исход не может быть получен в результате принятия решения одним лицом.

Другим предшественником теории игр по праву считается французский математик Э. Борель (1871-1956). Некоторые фундаментальные идеи были независимо предложены А. Вальдом (1902-1950), заложившим основы нового подхода к статистической теории принятия решений.

Первые приложения теория игр нашла в математической статистике. Во время второй мировой войны и сразу после нее теорией игр серьезно заинтересовались военные, которые увидели в ней аппарат для исследования стратегических решений. Ее использовали как плодотворный источник теоретических моделей в экономике и социологии. Методы теории игр используются также в теории операций и в линейном программировании.

В начальной школе для обучения детей используют различные правила и инструкции, поэтому в этом возрасте можно развивать у них алгоритмическое мышление, которое не только приводит к более прочному усвоению знаний, но и к вхождению в компьютерный мир.

Изучение "Теории игр" в начальной школе поможет сформировать у детей умение анализировать условие задачи, продумывать последовательность действий, направленных на ее выполнение. Контролировать правильность своих действий на всех этапах работы и корректировать их в случаях допущенной ошибки, то есть направить учащихся на формирование широкого спектра умений, которые будут необходимы в дальнейшей учебной и учебно-трудовой деятельности ребенка, а в будущем и любой профессиональной деятельности.

Цель: изучение теоретических положений по теории игр и создание элективного курса "Элементы теории игр в начальной школе" с методической поддержкой.

Объект исследования: Теория игр

Предмет исследования: Обучение теории игр в начальной школе.

Задачи исследования:

изучить теоретический материал

отобрать задачи для практической реализации

разработать алгоритмы решения задач

программно реализовать отобранные задачи

разработать элективный курс

создать электронное пособие

Гипотеза: если в процессе обучения использовать понятие выигрышной стратегии, то это будет способствовать развитию логического мышления и сообразительности у младших школьников, а также повысит общий уровень подготовки по информатике.

Новизна работы заключается в следующем:

На данный момент не существует школьного курса по теме теории игр в начальной школе.

Создана программная поддержка, позволяющая осуществить эффективное изучение данной темы в начальной школе.

Разработан элективный курс “Элементы теории игр в начальной школе" и программно-методическая поддержка к нему.

Глава I Основные положения Теории игр

1.1 Предмет и задачи теории игр

В процессе целенаправленной человеческой деятельности возникают ситуации, в которых интересы отдельных лиц (участников, групп, сторон) либо прямо противоположны (антагонистичны), либо, не будучи непримиримыми, все же не совпадают. Простейшими и наиболее наглядными примерами таких ситуаций являются спортивные игры, арбитражные споры, военные учения (маневры), борьба между блоками избирателей за своих кандидатов, в международных отношениях - отстаивание интересов своего государства и т.п. Здесь каждый из участников сознательно стремится добиться наилучшего результата за счет другого участника. Подобного рода ситуации встречаются и в различных сферах производственной деятельности.

Все ситуации, когда эффективность действия одного из участников зависит от действий других, можно разбить на два типа: интересы участников совпадают, и они могут договориться о совместных действиях; интересы участников не совпадают. В этих случаях может оказаться невыгодным сообщать другим участникам свои решения, так как кто-нибудь из них сможет воспользоваться знанием чужих решений и получит больший выигрыш за счет других участников. Ситуации такого типа называются конфликтными.

Для указанных ситуаций характерно, что эффективность решений, принимаемых в ходе конфликта каждой из сторон, существенно зависит от действий другой стороны. При этом ни одна из сторон не может полностью контролировать положение, так как и той и другой стороне решения приходится принимать в условиях неопределенности. Так, при определении объема выпуска продукции на одном предприятии нельзя не учитывать размеров выпуска аналогичной продукции на других предприятиях. В реальных условиях нередко возникают ситуации, в которых антагонизм отсутствует, но существуют противоположные тенденции. Например, для нормального функционирования производства, с одной стороны, необходимо наличие запасов разнообразных ресурсов, но с другой - стремление к чрезвычайному увеличению этих запасов вызывает дополнительные затраты по их содержанию и хранению. В приведенных примерах конфликтные ситуации возникают в результате сознательной деятельности людей. Однако на практике встречаются неопределенности, которые порождаются не сознательным противодействием другой стороны, а недостаточной информированностью об условиях проведения планируемой операции.

Раздел математики, изучающий конфликтные ситуации на основе их математических моделей, называется теорией игр. Таким образом, теория игр - это математическая теория конфликтных ситуаций, разрабатывающая рекомендации по наиболее рациональному образу действий каждого из участников в ходе конфликтной ситуации, т.е. таких действий, которые обеспечивали бы ему наилучший результат. Игровую схему можно придать многим ситуациям в экономике. Здесь выигрышем могут быть эффективность использования дефицитных ресурсов, производственных фондов, величина прибыли, себестоимость и т.д.

Необходимо подчеркнуть, что методы и рекомендации теории игр разрабатываются применительно к таким специфическим конфликтным ситуациям, которые обладают свойством многократной повторяемости. Если конфликтная ситуация реализуется однократно или ограниченное число раз, то рекомендации теории игр теряют смысл.

Чтобы проанализировать конфликтную ситуацию по ее математической модели, ситуацию необходимо упростить, учтя лишь важнейшие факторы, существенно влияющие на ход конфликта.

Определение 1. Игрой называется упрощенная математическая модель конфликтной ситуации, отличающаяся от реального конфликта тем, что ведется по определенным правилам.

Игра - это совокупность правил, определяющих возможные действия (чистые стратегии) участников игры. Суть игры в том, что каждый из участников принимает такие решения в развивающейся конфликтной ситуации, которые, как он полагает, могут обеспечить ему наилучший исход. Исход игры - это значение некоторой функции, называемой функцией выигрыша (платежной функцией), которая может задаваться либо аналитически выражением, либо таблично (матрицей). Величина выигрыша зависит от стратегии, применяемой игроком.

Человечество издавна пользуется такими формализованными моделями конфликтных ситуаций, которые являются играми в буквальном смысле слова. Примерами могут служить шашки, шахматы, карточные игры и т.д. Все эти игры носят характер соревнования, протекающего по известным правилам и заканчивающего "победой" (выигрышем) того или иного игрока.

Такие формально регламентированные, искусственно организованные игры представляют собой наиболее подходящий материал для иллюстрации и усвоения основных понятий теории игр. Терминология, заимствованная из практики таких игр, применяется и при анализе других конфликтных ситуаций: стороны, участвующие в них, условно именуются "игроками", а результат столкновения - "выигрышем" одной из сторон.

Определение 2.Под "правилами игры" подразумевается система условий, регламентирующая возможные варианты действий обеих сторон.

Определение 3. Стратегией игрока называется совокупность правил, однозначно определяющих последовательность действий игрока в каждой конкретной ситуации, складывающейся в процессе игры.

Определение 4. Оптимальной называется стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш.

Основное предположение, исходя из которого находят оптимальные стратегии, состоит в том, что противник по меньшей мере так же разумен, как и сам игрок, и делает все для того, чтобы добиться своей цели.

Количество стратегий у каждого игрока может быть конечным или бесконечным, в зависимости от этого игры подразделяются на конечные и бесконечные.

Всякая игра состоит из отдельных партий.

Определение 5. Партией называется каждый вариант реализации игры определенным образом.

В свою очередь, в партии игроки совершают конкретные ходы.

Определение 6. Ходом называется выбор и реализация игроком одного из допустимых вариантов поведения.

Ходы бывают личные и случайные. При личном ходе игрок самостоятельно и осознанно выбирает и реализует ту или иную чистую стратегию. Набор возможных вариантов при каждом личном ходе регламентирован правилами игры и зависит от всей совокупности предшествующих ходов обеих сторон. Например, в шахматах каждый ход является личным. При случайном ходе выбор чистой стратегии производится с использованием какого-либо механизма случайного выбора, например с применением таблицы случайных чисел. Примером могут служить бросание монеты или игральной кости.

Конфликтные ситуации, встречающиеся в практике, порождают различные виды игр. Классифицировать игры можно по разным признакам. Различают, например, игры по количеству игроков. В игре может участвовать любое конечное число игроков.

Определение 7.Если в игре игроки объединяются в две группы, преследующие противоположные цели, то такая игра называется игрой двух лиц (парная игра).

В зависимости от количества стратегий в игре они делятся на конечные или бесконечные. В зависимости от взаимоотношений участников различают игры бескоалиционные (участники не имеют права заключать соглашения), или некооперативные, и коалиционные, или кооперативные. По характеру выигрышей игры делятся на игры с нулевой суммой и ненулевой суммой.

Определение 8. Игрой с нулевой суммой называется игра, в которой общий капитал игроков не меняется, а лишь перераспределяется в ходе игры, в связи с чем сумма выигрышей равна нулю (проигрыш принимается как отрицательный выигрыш).

В играх с ненулевой суммой сумма выигрышей отлична от нуля. Например, при проведении лотереи часть взноса участников идет организатору лотереи.

По виду функции выигрыша игры делятся на матричные, биматричные, непрерывные, выпуклые, сепарабельные и др.

Определение 9. Матричной игрой (при двух участниках) называется игра, в которой выигрыши первого игрока (проигрыши второго игрока) задаются матрицей.

В биматричных играх выигрыши каждого игрока задаются своей матрицей. Другие типы таких игр различаются видом аналитического выражения платежной функции. По количеству ходов игры делятся на одноходовые (выигрыш распределяется после одного хода каждого игрока) и многоходовые (выигрыш распределяется после нескольких ходов). Многоходовые игры в свою очередь делятся на позиционные, стохастические, дифференциальные и др. В зависимости от объема имеющейся информации различают игры с полной и неполной информацией.

В реальных конфликтных ситуациях каждый из игроков сознательно стремится найти наилучшее для себя поведение, имея общее представление о множестве допустимых для партнера ответных действий, но не ведая о том, какое же конкретное решение будет выбрано им в данный момент. В этом проявляется в равной мере неопределенность ситуации для каждого из партнеров.

Определение 10.Игры, в которых участники стремятся добиться для себя наилучшего результата, сознательно выбирая допустимые правилами игры способы действий, называются стратегическими.

Однако в экономической практике нередко приходится формализовать (моделировать) ситуации, придавая им игровую схему, в которых один из участников безразличен к результату игры. Такие игры называют играми с природой, понимая под термином "природа" всю совокупность внешних обстоятельств, в которых сознательному игроку (его называют иногда статистиком, а соответствующую игру - статистической) приходится принимать решение. Например, выбор агрономической службой сельскохозяйственного предприятия участков для посева той или иной культуры в надежде получить в предстоящем году наилучший урожай; определение объема выпуска сезонной продукции в ожидании наиболее выгодного для ее реализации уровня спроса; формирование пакета ценных бумаг в расчете на высокие дивиденды и т.п. Здесь в качестве второго игрока выступает: в первом примере - в буквальном смысле природа; во втором - уровень спроса; в третьем - размеры ожидаемой прибыли.

В играх с природой степень неопределенности для сознательного игрока (статистика) возрастает: если в стратегических играх каждый из участников постоянно ожидает наихудшего для себя ответного действия партнера, то в статистических играх "природа", будучи индифферентной в отношении выигрыша инстанцией, может предпринимать и такие ответные действия (будем говорить: реализовывать такие состояния), которые ей совершенно невыгодны, а выгодны сознательному игроку (статистику).

В дальнейшем мы будем рассматривать только парные матричные игры с нулевой суммой. Так как в случае конечной игры двух лиц функции выигрыша каждого из игроков удобно представлять в виде матрицы выигрышей, где строки представляют стратегии одного игрока, столбцы - стратегии другого игрока, а в клетках матрицы указываются выигрыши каждого из игроков в каждой из образующихся ситуаций. (9, 16, 17, 40, 46)

1.2 Решение матричной игры в чистых стратегиях

Рассмотрим простейшую математическую модель конечной конфликтной ситуации, в которой имеется два участника и выигрыш одного равен проигрышу другого. Такая модель называется антагонистической игрой двух лиц с нулевой суммой. Игра состоит из двух ходов: игрок А выбирает одну из возможных стратегий А_i, , а игрок В выбирает одну из возможных стратегий В_j, . Каждый выбор производится при полном незнании выбора соперника. В результате выигрыш игроков составит соответственно a_ij и - a_ij. Цель игрока А - максимизировать величину a_ij, а игрока В - минимизировать эту величину.

Определение 1. Матрица, составленная из величин a_ij, ,,

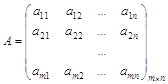
называется платежной матрицей, или матрицей игры. Каждый элемент платежной матрицыa_ij, ,равен выигрышу А (проигрышу В), если он выбрал стратегию А_i, , а игрок В выбирал стратегию В_j, .

Пример. В игре участвуют первый и второй игроки, каждый из них может записать независимо от другого цифры 1, 2 и 3. Если разность между цифрами, записанная игроками, положительна, то первый игрок выигрывает количество очков, равное разности между цифрами, и, наоборот, если разность отрицательна, то выигрывает второй игрок. Если разность равна нулю, то игра заканчивается вничью.

У первого игрока три стратегии (варианта действия): А₁ (записать 1), А₂ (записать 2), А₃ (записать 3); у второго игрока также три стратегии: В₁, В₂, В_{3 (}табл.1).

Таблица 1