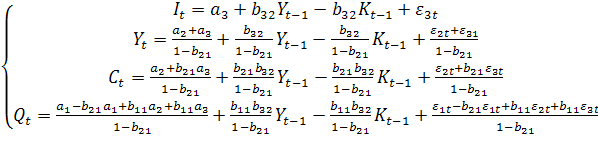Уравнения регрессии
УГСХА
Контрольная работа
по дисциплине «Эконометрика»
студента 1 курса
заочного отделения
экономического факультета
специальность 060500
«Финансы и кредит»
Кириллова Юрия Юрьевича
шифр 07045
Ульяновск 2008
Задание 1
Рассчитанные параметры уравнений линейной (I), степенной (II), полулогарифмической (III), обратной (IV), гиперболической парной (V), экспоненциальной (VI) регрессии приведены в таблице 1.
Во всех 6 уравнениях связь умеренная (r ~ 0.5), однако в уравнении IV связь обратная, во всех остальных – прямая. Коэффициент детерминации r² также различается не сильно. Наиболее сильное влияние вариации фактора на вариацию результата в уравнении I, наиболее слабое в уравнении V.
Средний коэффициент эластичности колеблется от 0,1277 в уравнении V до 0,1628 в уравнении III, из чего можно сделать вывод о слабом влиянии прожиточного минимума на размер пенсий.
Средняя ошибка аппроксимации чрезвычайно высока (96%) для третьего уравнения и незначительна (~3%) для остальных пяти.
Fтабл.=4,84 для α=0,05. Неравенство Fтабл. Итак, уравнение линейной регрессии является лучшим уравнением регрессии, применительно к данной задаче. Оно статистически надежно, обладает невысокой ошибкой аппроксимации и умеренным коэффициентом корелляции. Для уровня значимости α=0,05 доверительный интервал прогноза результата, при увеличении прогнозного значения фактора на 10% для уравнения I 231,44±19,324, для уравнения II 231,52±0,0377, для уравнения III 455,06±19,953, для уравнения IV 231,96±20,594, для уравнения V 231,39±0,0004, для уравнения VI 231,17±0,0842. Задание 2 Таблица 2. Исходные данные задания 2 (n=25). Для расчета значимости уравнений сначала необходимо найти стандартизированные коэффициенты регрессии по формуле По этой формуле получаем в первом уравнении β₁=0,6857, β₂=-0,2286, во втором уравнении β₁=0,7543, в третьем уравнении β₂=-0,4686. Из стандартизированных уравнений находим для первого уравнения Для второго уравнения для третьего Для второго и третьего уравнений Δr₁₁=1. Находим Для первого уравнения получаем Далее находим F-критерий Фишера Для первого уравнения Fфакт.=18,906>Fтабл.=3,44, что подтверждает статистическую значимость уравнения. Для второго уравнения Fфакт.=30,360>Fтабл.=4,28, что подтверждает статистическую значимость уравнения. Для третьего уравнения Fфакт.=6,472>Fтабл.=4,28, что подтверждает его статистическую значимость. Итак, F-критерий Фишера подтверждает значимость всех трех уравнений с вероятностью 95%. Для оценки значимости коэффициентов регрессии первого уравнения вычисляем t-критерий Стьюдента где частный F-критерий Получаем Показатели частной корелляции для первого уравнения вычисляются по формуле Получаем Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле Для первого уравнения получаем Задание 3 Исходная система уравнений содержит эндогенные четыре переменные В соответствии с необходимым условием идентификации D+1=H первое и второе уравнения сверхидентифицируемы (H=2, D=2), третье уравнение идентифицируемо (H=1, D=0), четвертое уравнение является тождеством и в проверке не нуждается. Для первого уравнения Для второго уравнения Для третьего уравнения Четвертое уравнение является тождеством и в проверке не нуждается. Достаточное условие идентификации выполняется для всех уравнений. Для оценки параметров данной модели применяется двухшаговый МНК. Приведенная форма модели ~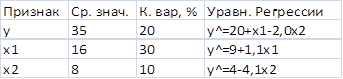
.
, 
, для второго уравнения 
, для третьего 
. Далее находим Δr и Δr₁₁. Для первого уравнения
,
.
,
.
.
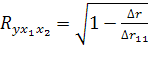, для второго 
, для третьего 
.
.
,
.
, 
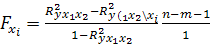. Отсюда 
, 
. Для α=0,05 
. Следовательно, коэффициент регрессии b₁ является статистически значимым, а коэффициент b₂ таковым не является.
.
, 
.
.
, 
, для второго уравнения 
, для третьего уравнения 
.
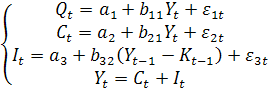
и две предопределенные 
.
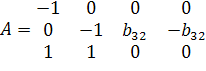, Det A*≠0, rk A=3.
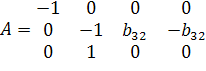, Det A*≠0, rk A=3.
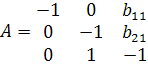, Det A*≠0, rk A=3.
~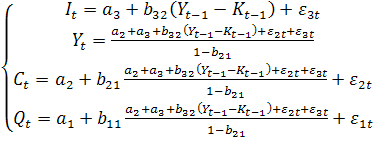