Среднеарифметический и среднегармонический индексы в анализе рыночных процессов
Глава 1. Теоретические основы среднеарифметического и среднегармонического индексов в анализе рыночных процессов
1.1 Понятие средней величины
1.2 Понятие индексов
1.3 Понятие о среднеарифметическом и среднегармоническом индексах
Глава 2. Расчетная часть
Задание 1
Задание 2
Задание 3
Задание 4
Глава 3. Аналитическая часть
3.1 Постановка задачи
3.2 Методика решения задачи
3.3 Технология выполнения компьютерных расчетов
Заключение
Список литературы
Введение
Методы статистики - это особые приемы и способы изучения массовых общественных явлений. Каждый метод ориентирован на особые представления изучаемого объекта, на его особую модель. Индексы являются незаменимым инструментом исследования в тех случаях, когда необходимо сравнить во времени или в пространстве две совокупности, элементы которых являются несоизмеримыми величинами. И поскольку объекты изучения индексов весьма разнообразны, то они широко применяются в экономической практике(1).
Целью работы является изучение методологии вычисления среднеарифметического и среднегармонического индексов (на примере индексов цен и физического объёма товарооборота).
Задачами работы являются: изучение среднеарифметического и среднегармонического индексов, решение задач по основам статистики и проведение статистического анализа конкретного явления.
В ходе выполнения работы применялись следующие методы исследования: монографический (использование специальной литературы), аналитический, расчётный, сравнение.
В теоретической части рассмотрены понятие о средних величинах вообще, понятие о индексах и понятие среднеарифметического и среднегармонического индексов с применением их в анализе рыночных отношений.
В расчетной части решены практические задания.
В аналитической части проведен анализ зависимости числа преступлений от количества безработных в центральном регионе России с применением пакета прикладных программ обработки электронных таблиц MSExcel в среде Windows.
Глава 1. Теоретические основы среднеарифметического и среднегармонического индексов в анализе рыночных процессов
1.1 Понятие средней величины
В процессе обработки и обобщения статистических данных возникает необходимость определения средних величин. Как правило, индивидуальные значения одного и того же признака у различных единиц совокупности неодинаковы. Средняя величина - обобщающая характеристика изучаемого признака в исследуемой совокупности..Она отражает его типичный уровень в расчете па единицу совокупности в конкретных условиях места и времени..
Например, при изучении доходов рабочих концерна обобщающей характеристикой служит средний доход одного рабочего. Для его определения общую сумму средств, направленных на потребление, в виде заработной платы, социальных и трудовых льгот, материальной помощи, дивидендов по акциям и процентов по вкладам в имущество концерна за рассматриваемый период (год, квартал, месяц) делят на численность рабочих концерна.
Естественно, индивидуальные значения дохода отдельных рабочих отличаются от среднего уровня в силу ряда причин (квалификации, стажа работы, наличия акций, суммы вклада в имущество концерна и др.). Средний доход в свою очередь характеризует то общее, что свойственно всей совокупности рабочих предприятия, т.е. уровень дохода массы рабочих в конкретных условиях функционирования данного концерна в рассматриваемом периоде.
При исчислении средней величины по массе единиц влияние случайных причин взаимопогашается, и средняя, абстрагируясь от индивидуальных особенностей отдельных единиц совокупности, выражает общие свойства, присущие всем единицам. Кетлс подчеркивал, что статистические средние представляют собой не просто метод математического измерения, а категорию объективной действительности. Принципиальная суть статистического познания состоит в погашении случайного, вызванного действием индивидуальных причин, и в выявлении закономерностей, обусловленных общими причинами.
Средние величины применяются для оценки достигнутого уровня изучаемого показателя, при анализе и планировании производственно-хозяйственной деятельности предприятий (объединений), фирм, банков и других хозяйственных единиц; средние используются при выявлении взаимосвязей явлений, при прогнозировании, а также расчете нормативов. Средняя величина всегда именованная, имеет ту же размерность (единицу измерения), что и признак у отдельных единиц совокупности.
Простая средняя арифметическая определяется по формуле:
![]() ; (1)
; (1)
где X. - индивидуальное значение признака каждой единицы совокупности; п - число единиц совокупности.
Итак, при выборе вида средней величины обычно исходят из логической сущности усредняемого признака и его взаимосвязи с итоговым (определяющим) показателем. Величина итогового показателя не должна изменяться при замене индивидуальных значений признака средней величиной.
Способность средних величин сохранять свойства статистических совокупностей называют определяющим свойством.
Общая формула степенной средней записывается следующим образом:
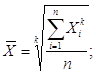 (2)
(2)
При k=-1 получим среднюю гармоническую величину:
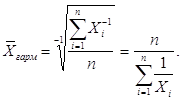 (3)
(3)
1.2 Понятие индексов
В статистике под индексом понимается относительная величина (показатель), выражающая изменение сложного экономического явления во времени, в пространстве или по сравнению с планом. В связи с этим различают динамические, территориальные индексы, а также индексы выполнения плана.
Многие общественные явления состоят из непосредственно несопоставимых явлений, поэтому основной вопрос - это вопрос сопоставимости сравниваемых явлений.
К какому бы экономическому явлению ни относились индексы, чтобы рассчитать их, необходимо сравнивать различные уровни, которые относятся либо к различным периодам времени, либо к плановому заданию, либо к различным территориям. В связи с этим различают базисный период (период, к которому относится величина, подвергаемая сравнению) и отчетный период (период, к которому относится сравниваемая величина). При исчислении важно правильно выбрать период, принимаемый за базу сравнения.
Индексы классифицируют по трем признакам: по характеру изучаемых объектов; степени охвата элементов совокупности; методам расчета общих индексов. По содержанию индексируемых величин индексы разделяют на индексы количественных (объемных) и индексы качественных показателей - эти индексы будут рассматриваться нами ниже в полном объеме. Индексы могут относиться либо к отдельным элементам сложного экономического явления, либо ко всему явлению в целом.
Индивидуальные индексы.
Показатели, характеризующие изменение более или менее однородных объектов, входящих в состав сложного явления, называются индивидуальными индексами. Индивидуальные индексы обозначаются i и снабжаются подстрочным знаком индексируемого показателя. Индивидуальные индексы относятся к одному элементу и не требуют суммирования данных. Они представляют собой относительные величины динамики, выполнения обязательств, сравнения. Выбор базы сравнения определяется целью исследования. Название индекс получает по названию индексируемой величины. В большинстве случаев в числителе стоит текущий уровень, а в знаменателе - базисный уровень. Исключением является индекс покупательной способности рубля. Индексы измеряются либо в виде процентов, либо в виде коэффициентов.
Общие индексы
Общие индексы отражают изменение всех элементов сложного явления. При этом под сложным явлением понимают такую статистическую совокупность, отдельные элементы которой непосредственно не подлежат суммированию (физический объем продукции, включающей разноименные товары цены на разные группы продуктов и т.д.). Общие индексы обозначаются буквой I и также сопровождаются подстрочным знаком индексируемого показателя. Методика расчета общих индексов сложнее, чем индивидуальных, и различна в зависимости от характера индексируемых показателей, наличия исходных данных и целей исследования.
Сводные индексы
Сложные явления, для которых рассчитывается сводный индекс, отличаются той особенностью, что элементы, их составляющие, неоднородны и, как правило, несоизмеримы друг с другом. Поэтому сопоставление простых сумм этих элементов невозможно. Сопоставимость может быть достигнута различными способами:
1) сложные явления могут быть разбиты на такие простые элементы, которые в известной степени являются однородными;
2) сравнение по стоимости, без разбиения на отдельные элементы.
Цель теории индексов - изучение способов получения относительных величин, используемых для расчета общего изменения ряда разнородных явлений.
Сводные индексы в агрегатной форме позволяют нам измерить не только относительное изменение отдельных элементов изучаемого явления и явления в целом в текущем периоде по сравнению с базисным, но и абсолютное изменение.(2)
1.3 Понятие о среднеарифметическом и среднегармоническом индексах
Индексы количественных показателей.
Необходимость в применении особых приемов построения индексов количественных показателей возникает, когда итоги по отдельным элементам сложного явления непосредственно несоизмеримы. Например, предприятие экспортирует станки, металл, товары широкого потребления. Если имеются сведения об экспорте продукции только в натуральном выражении, то динамику экспорта продукции предприятия в целом нельзя охарактеризовать показателем
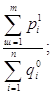 г
г
де qi - количество продукции данного вида в натуральном выражении.
Различные виды продукции неравноценны по количеству затраченного на них общественного труда и имеют разные потребительные стоимости. Поэтому было бы неправильно непосредственно суммировать итоги по этим видам продукции. Для получения общего итога необходимо данные по различным видам продукции привести к единой, общей мере, например, использовать стоимостную оценку экспорта продукции.
Если разделить стоимость продукции отчетного периода на стоимость продукции базисного периода, получим индекс стоимости продукции. В общем виде его можно записать:
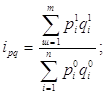 (4)
(4)
Приведенная формула характеризует изменение стоимости продукции, которая зависит от изменения уровня цен и количества выпускаемой продукции в отчетном периоде по сравнению с базисным. Поэтому индекс стоимости не дает количественного представления об изменении объема выпуска. Это представление мы получим, если элиминируем влияние изменения цен, для чего количество продукции, произведенной в отчетном и базисном периодах, умножим на одинаковые для обоих периодов цены:
 (5)
(5)
Такой индекс называют агрегатным индексом физического объема.
При вычислении индекса физического объема продукции возможны разные решения в зависимости от выбора коэффициента соизмерения.
Если принять за коэффициент соизмерения цены базисного периода, то индекс физического объема продукции будет иметь следующий вид:
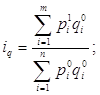 (6)
(6)
Такой вариант построения агрегатного индекса был предложен Э. Ласпейрссом в 1864 г.
Внешней отличительной особенностью агрегатного индекса является то, что в числителе и в знаменателе меняется индексируемая величина, значения же другой, являющейся соизмерителем, остаются неизменными. В приведенном варианте индекса количественных показателей значения соизмерителей принимаются на уровне базисного периода. Используя коэффициенты соизмерения базисного периода, берут базисные соотношения по yровню цен, но зато полностью элиминируют влияние на изменение стоимости продукции изменения самих цен.
В практике планирования при проведении экономико-статистического анализа не ограничиваются исчислением отдельных изолированных индексов, характеризующих изменение показателя за какой-то один период времени. Исчисляют, как правило не один индекс, а несколько индексов за последовательные периоды времени. При таком исчислении обычно применяют во всех индексах в качестве соизмерителей цены одного и того же периода. Например, для динамических сопоставлений роста выпуска объема продукции в промышленности, строительстве и т.д. Такие цены называются сопоставимыми (фиксированными или неизменными); в условиях стабильной экономики они применяются на протяжении длительного периода времени. При существенных различиях в соотношении уровней действующих и фиксированных цен производится пересмотр последних, и они меняются время от времени с изменением особенностей самого ценно- образования. В настоящее время в странах СНГ, учитывая нестабильное состояние экономики, при расчетах динамики валового; внутреннего продукта, национального богатства в качестве фиксированных используют цены предыдущего года.
Применяя в качестве соизмерителя неизменные цены, получим следующую формулу индекса физического объема продукции:
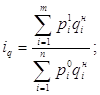 (7)
(7)
Преимущество такого варианта соизмерения продукции состоит и в том, что путем суммирования может быть получен итоговый показатель за период любой продолжительности, т.е. на основе данных о стоимости продукции за каждый месяц можно получить стоимость продукции за квартал, полугодие, год. Использование неизменных цен в учете продукции дает возможность изучать динамику выпуска не только отдельных видов продукции, но и по предприятиям, отраслям промышленности и промышленности в целом.
Агрегатный индекс с соизмерителями отчетного периода был предложен в 1874 г. Г. Пааше (Paashe).
Рассмотрим порядок вычисления индексов физического объема продукции на следующем условном примере. Имеются данные (табл.1) о фактическом выпуске продукции машиностроительным предприятием за два года:
Таблица 1
Объем выпуска продукции ОАО «Северсталь» по видам
| Виды продукции | Выпуск продукции в натуральном выражении | Цена производителя за единицу, млн руб. | Индивидуальные индексы физического объема продукции . я) 4 < | Индивидуальные индексы цен | ||
| базисный период | отчетный период | базисного периода | отчетного периода | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Оборудование, шт. | 2100 | 2000 | 75,00 | 82,50 | 0,9524 | 1,1000 |
| Литье, т | 11 500 | 12 000 | 8,75 | 10,10 | 1,0435 | 1,1543 |
По данным о выпуске продукции в натуральном выражении можно рассчитать индексы, характеризующие динамику выпуска отдельных видов продукции, или индивидуальные индексы. Индивидуальный индекс показывает, во сколько раз изменилось производство данного вида продукции в отчетном периоде по отношению к периоду, с которым проводилось сравнение.
Для вычисления индивидуальных индексов динамики определяют отношение объема выпуска продукции отчетного периода к объему выпуска в предшествующем периоде (см. гр. 6 табл.1):
 (8)
(8)
Индекс динамики объема производства оборудования составляет 95,24%, что означает снижение его выпуска на 4,7б%. В динамике же выпуска литья наблюдается противоположная тенденция: выпуск литья возрос па 4,35%. Общее изменение выпуска продукции предприятия может быть получено на основе определения агрегатной формы индекса физического объема продукции. Покажем расчет агрегатных индексов физического объема продукции в двух ва -риантах:
1) в качестве соизмерителей используются цены базисного периода - формула и 2) соизмерителями разнородной продукции предприятия являются текущие цены (цены отчетного периода). Стоимостные показатели выпуска продукции, необходимые для расчета индексов, приведены в табл. 2.
Таблица 2
Расчет стоимости выпуска продукции (млн. руб.)
| Виды продукции | Стоимость выпуска | Условная стоимость выпуска | Доля изделий в стоимости продукции предприятия j | |||
| базисного периода | отчетного периода | базисного периода в текущих ценах Р/Ч° | отчетного периода в базисных ценах р/Ч' | базисного периода | Отчётного периода | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Оборудо-вание | 157 500 | 165 000 | 173 250 | 150 000 | 0,6102 | 0,5765 |
| Литье | 100 625 | 121 200 | 116 150 | 105 000 | 0,3898 | 0,4235 |
| Итого | 258 125 | 286 200 | 289 400 | 255 000 | 1.0000 | 1.0000 |
Агрегатный индекс динамики физического объема продукции, рассчитанный по формуле Ласпейреса, составит 0,9879:
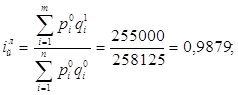
т.е. физический объем выпуска продукции предприятия снизился в отчетном периоде на 1,21%.
Величина агрегатного индекса физического объема, рассчитанная по формуле Пааше, равна 0,98894:
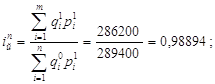
т.е. физический объем выпуска продукции предприятия уменьшился на 1,106%.
Если сопоставить величины двух индексов,то несмотря на некоторые отличия в величине, они отражают одну и ту же тенденцию - снижение физического объема выпуска продукции предприятия.
Величина агрегатного индекса физического объема зависит от индивидуальных индексов, так как общее изменение объема производимой продукции (при неизменности ассортимента) есть результат изменения объема выпуска каждого отдельного вида. Общий результат изменения определяется также удельным весом стоимости отдельных видов продукции в общей стоимости продукции.
Общий индекс физического объема, построенный на базе индивидуальных индексов, принимает форму среднего арифметического или гармонического индекса. Например, известна стоимость продукции каждого вида в базисном периоде и индивидуальные индексы физического объема. Исходной базой построения среднего из индивидуальных индексов служит агрегатная форма индекса Ласпейреса (6).
Из имеющихся данных непосредственно суммированием можно получить только знаменатель формулы. Числитель же может быть получен перемножением стоимости отдельного вида продукции базисного периода на индивидуальный индекс.
Тогда формула агрегатного индекса физического объема принимает вид:
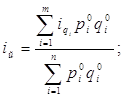 (9)
(9)
т.е. получим средний арифметический индекс физического объема, где весами служит стоимость отдельных видов продукции в базисном периоде. При выборе весов следует иметь в виду, что средний индекс должен быть тождествен агрегатному, который является основной формой индекса. Учитывая, что отношение
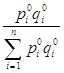
характеризует долю данного вида продукции в общей стоимости продукции базисного периода (di0), средний арифметический индекс физического объема будет иметь вид:
![]() (10)
(10)
Воспользуемся данными гр. 6 табл. 1 и гр. 2 табл. 2 для расчета среднего арифметического индекса физического объема продукции:
![]()
т.е. получим такой же результат, как и при расчете агрегатного индекса физического объема по формуле Ласпейреса.
Снижение общего объема выпуска продукции предприятия на 1,21% объясняется тем, что превалирующее влияние на величину агрегатного индекса оказывает изменение физического объема выпуска оборудования, поскольку доля оборудования в стоимости продукции предприятия в базисном периоде составляла 61,02% (см.гр. 6 табл. 2).
Допустим, что в наличии имеется информация о динамике объема выпуска каждого вида продукции и стоимость, каждого вида продукции в отчетном периоде.
Для определения общего изменения выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше, так как числитель формулы можно получить суммированием величин, а знаменатель - делением фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс
физического объема продукции.
Тогда:  (11)
(11)
Таким образом, в этом случае расчет выполняется по формуле среднего взвешенного гармонического индекса физического объема и величина его будет равна 0,98896 (используем данные гр. 6 табл.1 и гр. 3 табл.2):
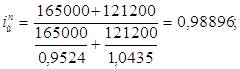
Вместе с тем общий индекс физического объема продукции не всегда может быть представлен средней величиной из индивидуальных индексов. Этого нельзя сделать в том случае, когда перечень (номенклатура) изделий в текущем периоде не совпадает с их перечнем в базисном периоде, т.е. средние индексы могут быть рассчитаны лишь по сравнимому кругу изделий. По несравнимой продукции нельзя определить индивидуальные индексы, а потому становится невозможным преобразование агрегатного индекса в адекватные ему средние индексы.
В промышленности наблюдается непрерывное обновление ассортимента выпускаемой продукции, в связи с чем объем выпуска ряда новых видов изделий не может быть сопоставлен ни с одним из предшествующих периодов. Если строго придерживаться формулы агрегатного индекса, то пришлось бы определить ин-дексы физического объема не по всей продукции, а только по тем ее видам, которые вырабатывались на протяжении всех изучаемых периодов времени. Индекс же физического объема продукции должен отразить изменение в общем объеме выпуска, которое происходит как вследствие увеличения (уменьшения) выпуска изделий в отчетном периоде по сравнению с базисным, гак и в результате появления новых видов изделий или исключения старых, ранее изготовляемых изделий. Чтобы индекс продукции мог отразить указанные изменения, числитель индекса должен состоять из двух слагаемых: стоимости сравнимой продукции, т.е. продукции, которая изготавливалась и в предшествующие периоды, и стоимости несравнимой продукции, т.е. тех новых изделий, которые ранее не вырабатывались. В знаменателе индекса физического объема продукции приводится стоимость всей продукции базисного периода, включая стоимость и той продукции, которая в отчетном периоде уже не выпускается.
И, наконец, расчет агрегатных индексов может производиться на основе данных о стоимостных (а не натуральных) объемах выпуска каждого вида продукции и индивидуальных индексах цен. В условиях рыночной экономики мониторинг цен имеет первостепенное значение.
Индексы качественных показателей (на примере индекса цен).
Наряду с индексами физического объема продукции в планировании и статистико-экономическом анализе деятельности предприятий и отраслей широко применяются индексы качественных показателей: цен, себестоимости, производительности труда, средней заработной платы и т.д. Качественный показатель характеризует уровень изучаемого результативного показателя в расчете на количественную единицу и определяется как отношение данного результативного показателя к связанному с ним количественному показателю (фактору), на единицу которого он определяется. Например, себестоимость единицы продукции определяется как отношение суммы затрат на производство этого вида продукции к количеству единиц продукции данного вида; средняя заработная плата определяется делением фонда заработной платы на численность работников и т.д.
Формулы индексов качественных показателей рассмотрим на примере расчета индексов цен по данным табл.1.
Индивидуальные индексы цен
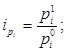 (12)
(12)
характеризуют относительное изменение уровня цен единицы каждого вида продукции в отчетном периоде по сравнению с базисным. Приведенные в гр. 7 табл.1 значения индивидуальных индексов цен показывают, что на оборудование цены выросли в 1,10 раза, или па 10%, а цены на литье - в 1,1543 раза, или на 15,43%.
Для определения общего изменения уровня цен на продукцию предприятия, включающую различные виды, нужно рассчитать агрегатный индекс цен. Непосредственное суммирование уровня цен одного станка и одной тонны литья не имеет экономического содержания. Несоизмеримость уровней в таком случае преодолевается путем взвешивания цены каждого вида продукции на количество произведенных единиц, т.е. для отчетного
и базисного периода определяются величины вида
![]()
которые и сравниваются между собой. Чтобы это сравнение отражало только изменение цен, необходимо, чтобы величина q фиксировалась в числителе и знаменателе индекса цен на уровне одного из периодов.
Общая формула агрегатного индекса цен записывается так:
 (13)
(13)
Очевидно, что как и в случае построения агрегатных индексов физического объема, возможен выбор в качестве веса количества продукции отчетного периода (формула Пааше) или количества продукции базисного периода (формула Ласпейреса).
Формула агрегатного индекса цен Ласпейреса:
 (14)
(14)
Воспользуемся данными табл.1 и итогами гр. 4 и 2 табл.2 для расчета этого индекса:
![]()
Полученная величина индекса означает, что цены на продукцию предприятия возросли в отчетном периоде па 12,12%. Формула агрегатного индекса цен Пааше:
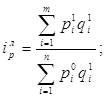 (15)
(15)
Используя данные табл.1 и 2, получим величину агрегатного индекса цен Пааше 1,1224:
![]()
По результатам расчета можно констатировать, что цены на всю продукцию предприятия возросли на 12,24%.
Широко применяется средний взвешенный гармонический индекс в статистике торговли при определении индексов розничных цен. Учет товарооборота ведется в денежном выражении но группам товаров, данные же о количестве проданных товаров в натуральном выражении во многих случаях отсутствуют. Поэтому непосредственно определить условную сумму товарооборота невозможно и тогда вместо агрегатной формы индекса вычисляется средний гармонический индекс с текущими весами (11).
Он алгебраически тождествен формуле Пааше и имеет точно такое же экономическое содержание.
Рассмотрим вычисление средних взвешенных индексов качественных показателей на примере. За отчетный месяц цена единицы изделия А возросла на 5% по сравнению с предыдущим месяцем, изделия Б - на 3%, изделия В - на 11%. Нужно определить общий (средний) процент роста цен по всем изделиям в отчетном месяце, если известно, что объем товарооборота в отчетном месяце составил (млн руб): по изделию А- 780, по изделию Б -520, по изделию В - 340. Имеющиеся данные представим в табл.3(гр.3 и 4).
Таблица З Динамика и структура товарооборота магазина
| Изделия | Объем товарооборота, Млн. руб. | Индивидуальные индексы цен | Условный объем товарооборота, Млн. руб. | Удельный вес стоимости изделия в общем объеме товарооборота | |||
| предшествующий месяц | отчетный месяц | отчетного месяца по ценам предыдущег | Предыду- щего месяца по ценам отчетного | Предыду- щего месяца | отчетного месяца | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| А | 750 | 780 | 1,05 | 742,86 | 787,5 | 47,02 | 47,56 |
| Б | 530 | 520 | 1,03 | 504,85 | 545,9 | 33,23 | 31,71 |
| В | 315 | 340 | 1,11 | 306,31 | 349,65 | 19,75 | 20, 73 |
| Итого | 1595 | 1640 | 1554,02 | 1683,05 | 100,00 | 100,00 | |
Определяем агрегатный индекс цен (по формуле Пааше):
 (16)
(16)
Числитель формулы приведен в итоговой строке гр. 3 табл. 3 равен 1640 млн. руб. Слагаемые знаменателя можно определить делением товарооборота данного вида продукции вотчетном году на индивидуальный индекс цен:
 (17)
(17)
Так, по изделию A этот индекс составит 742,86 млн. руб. и т.д. (см. гр. 5 табл.3).
Таким образом, получен общий объем товарооборота по ценам базисного периода. Общая его сумма стоит в знаменателе формулы. Разделив итог гр. 3 на итог гр. 5, получим, что в среднем цены возросли на 5,53%:
![]()
В данном случае агрегатный индекс цен представлен в форме среднего гармонического взвешенного индекса. В качестве весов используются фактические объемы товарооборота в отчетном месяце.
Поставим ту же задачу определения общего изменения цен на все изделия, но при условии, что известен товарооборот предыдущего месяца. Тогда при имеющейся информации об индивидуальных индексах цен и товарообороте предыдущего месяца (данные гр. 4 и 2 табл.3) рассчитать общий индекс цен можно с использованием агрегатного индекса Ласпейреса:
 (18)
(18)
В данном случае агрегатный индекс цен представлен формой среднего арифметического индекса, а в качестве весов используются фактические объемы товарооборота предыдущего месяца.
Учитывая, что
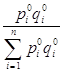
представляет собой удельный вес стоимости i-го изделия в общем объеме товарооборота предыдущего месяца, в качестве веса могут использоваться и показатели структуры товарооборота предыдущего месяца (см. гр. 7 табл.3). Используем итоги гр. 6 и 2 табл.3 для расчета агрегатного индекса цен и установим, что в среднем цены возросли на 5,52%:
![]()
Значения индексов iрп и iрл достаточно близки по величине, поскольку в структуре товарооборота в отчетном месяце не произошло значительных изменений, хотя нет и полного совпадения структуры товарооборота текущего и предшествующего месяца (сравните данные но строкам гр. 7 и 8 табл.3). Близость величины агрегатного индекса цен к величине индивидуального индекса цен изделия А объясняется тем, что на долю этого изделия приходится более 47% общего объема товарооборота. «Вклад» от -дельных изделий в общий рост цензависит от структуры товарооборота.
Приведенные варианты исчисления индексов отражают практику отечественной статистики. Во многих странах индексы физического объема и цен также исчисляются аналогичным образом.(3)
Глава 2. Расчетная часть
Задание 1
С целью изучения конъюнктуры рынка обследованы предприятия розничной торговли района (выборка 5%-ная механическая), в результате чего получены следующие данные за год о реализации условного товара А:
Таблица 4
Исходные данные
№ предприятия п/п | Объём продажи, т. | Средняя цена за 1 кг, руб. | № предприятя п/п | Объём продажи, т. | Средняя цена за 1 кг, руб. |
| 1 | 28 | 86 | 16 | 26 | 93 |
| 2 | 34 | 74 | 17 | 28 | 81 |
| 3 | 35 | 75 | 18 | 28 | 82 |
| 4 | 38 | 66 | 19 | 26 | 94 |
| 5 | 33 | 74 | 20 | 38 | 78 |
| 6 | 29 | 83 | 21 | 24 | 94 |
| 7 | 30 | 84 | 22 | 26 | 96 |
| 8 | 30 | 85 | 23 | 25 | 97 |
| 9 | 32 | 86 | 24 | 26 | 98 |
| 10 | 43 | 60 | 25 | 39 | 69 |
| 11 | 32 | 89 | 26 | 37 | 79 |
| 12 | 31 | 86 | 27 | 17 | 110 |
| 13 | 33 | 70 | 28 | 21 | 100 |
| 14 | 32 | 88 | 29 | 22 | 105 |
| 15 | 22 | 93 | 30 | 35 | 75 |
По исходным данным:
1. Постройте статистический ряд распределения предприятий по признаку – средняя цена товара, образовав пять групп с равными интервалами.
2. Рассчитайте характеристики интервального ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации, моду и медиану.
Сделайте выводы по результатам выполнения задания.
Решение
Построим статистический ряд распределения предприятий по признаку – средняя цена товара, образовав 5 групп с равными интервалами.
Определим величину интервала по средней цене продукции:
![]() руб.
руб.
где хmax - наибольший вариант, xmin - наименьший, - число групп.
Получим следующие интервальные группы предприятий по цене:
1 гр.: 60 – 70, 4 гр.: 90 – 100,
2 гр.: 70 – 80, 5 гр.: 100 – 110.
3 гр.: 80 – 90,
Таблица 5
Распределение предприятий по цене продукции
№ п/п | Ранжированный ряд по цене товара, руб. | Объём продажи, т. |
| 10 | 60 | 43<
Подобные работы:
Актуально:
|