Основы теории вероятности
Цель пособия
Цель создания данного пособия – на разных задачах, имеющих вероятностный характер, показать наиболее типичные алгоритмы их решения. С тем, чтобы не столько научить студента решать подобные задачи, сколько пробудить в нём интерес к теории вероятности.
На базе этого материала можно решать более сложные задачи теории вероятности.
Пособие будет полезным для самостоятельной работы студентов любых курсов специальностей: экономика, менеджмент, психология.
Раздел 1. Элементы комбинаторики
Соединения – это группы элементов некоторого конечного множества.
В элементарной алгебре рассматриваются 3 вида соединений: размещения, перестановки и сочетания (2)-(5). Остановимся на вопросе о подсчёте числа таких комбинаций.
Размещения – упорядоченные m-элементные подмножества данного множества из n элементов (m Число всех возможных комбинаций из n элементов по m обозначается Перестановки – упорядоченные n-элементные соединения из n элементов данного множества, отличающиеся лишь порядком элементов. Число перестановок из n элементов Например, Сочетания – неупорядоченные m-элементные соединения из n элементов данного множества, отличающиеся хотя бы одним элементом. Число различных сочетаний из n элементов по m обозначается символом Например, Кроме этого свойства числа сочетаний часто используется следующее: Кроме того, принята, по определению, запись: Задачи Задача №1. В розыгрыше первенства страны по футболу приняло участие 16 команд. Сколькими способами могут быть распределены золотые и серебряные медали? Решение. Золотую медаль может получить одна из 16 команд. После чего одна из 15 команд может иметь серебряную медаль. Общее число способов, которыми могут быть распределены золотая и серебряная медали, равно Задача №2. В кафе предлагают 5 первых блюд, 6 вторых и 4 третьих. Сколькими способами можно составить обед? Решение. Согласно правилу произведения число способов равно Задача №3. В классе изучают 10 предметов. В понедельник 6 уроков (все уроки разные). Сколькими способами можно составить расписание на понедельник? Решение. Здесь нужно воспользоваться формулой размещения из 10 элементов по 6: Задача №4. Сколькими способами можно разделить 6 шоколадок 14 лицам? (1 место – 1 плитка). Решение. 1.Все плитки различны. Число способов равно числу размещений из 14 по 6: 2.Все плитки одинаковы. Число способов равно числу сочетаний из 14 по 6: Задача №5. В группе 20 мальчиков и 20 девочек. Все умеют петь, танцевать, декламировать. Сколькими способами можно составить дуэты из учащихся групп? Решение. Число способов выбрать из 20 мальчиков певца, танцора и декламатора равно числу размещений из 20 по 3 - Задача №6. Необходимо укомплектовать экипаж космического корабля в составе: командир корабля, I его помощник, II его помощник, 2 бортинженера, 1 врач. Командующая тройка может быть отобрана из 25 готовящихся к полёту лётчиков; 2 бортинженера – из 20 специалистов, в совершенстве знающих устройство космического корабля; врач – из числа 8 медиков. Сколькими способами можно укомплектовать экипаж корабля? Решение. Задача №7. Из 30 последовательных натуральных чисел: 1, 2, 3, … 30 выбирают 3 числа так, чтобы их сумма была чётной. Сколько способов такого выбора? Решение. Сумма трёх чисел чётная, если все они чётные или из трёх 2 нечётные и 1 чётное. Например, 2 + 4 + 6 =12 и 3 + 5 + 2 = 10. Следовательно, число способов необходимого выбора равно сумме числа сочетаний из 15 чётных чисел по 3 и числа сочетаний из 15 нечётных чисел по 2, умноженного на число чётных, т.е. 15. Задача №8. Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли взять друг друга? Решение. Один из способов показан на рисунке, а общее число способов равно числу перестановок из восьми: рис.1 Задача №9. На тренировках занимаются 12 баскетболистов. Сколько разных стартовых пятёрок может образовать тренер? Решение. Т.к. нас интересует только состав, то имеем: Раздел 2. Классическое определение вероятности (теория урн) Вероятностью Р(А) события А называется отношение числа m результатов (исходов) эксперимента, благоприятствующих появлению события А, к числу n всех равновозможных результатов эксперимента: При этом Например, вероятность выпадения числа при одном бросании правильной монеты равна 1/2. Задачи Используя формулы и результаты решения задач раздела 1, решим задачи на вычисление вероятности события (по классическому определению). Задача №10. В урне 3 синих, 8 красных и 9 белых шаров, не различимых на ощупь. Шары тщательно перемешаны. Наудачу достают 1 шар. Найти варианты событий: извлечённый шар красный (событие А), синий (событие B), белый (событие С). Решение. Всего исходов эксперимента, состоящего в извлечении одного шара, 20=3+8+9, т.е. в формуле (2.1), n=20. Событию А благоприятствует 8 исходов, т.е. mА=8, аналогично mВ=3, mС=9. По формуле (2.1) имеем: Примечание. Если сложить полученные вероятности, то получим 1, т.е. Р(А) + Р(В) + Р(С) = 1, что говорит о том, что А, В и С составляют полную группу событий (см. раздел 3). Задача №11. В расписании 3 лекции по разным предметам. Всего на курсе изучается 10 предметов. Какова вероятность того, что студент, не знакомый с расписанием, угадает его, если все варианты составления расписания на день равновозможные. Решение. Всего комбинаций из 3-х предметов, выбранных из 10 и отличающихся друг от друга хоть одним предметом или порядком их следования, т.е. размещений из десяти элементов по три, можно получить: Нам нужна только одна комбинация Задача №12. На 8-ми одинаковых карточках написаны 2, 4, 6, 7, 8, 11, 12, 13. Найти вероятность того, что образованная из 2-х чисел дробь сократима. Решение. Всех исходов столько, сколько есть вариантов выбора двух карточек из 8 одинакового формата Þ Задача №13. Из 60 экзаменационных вопросов студент подготовил 50. Найти вероятность того, что вытянутый билет из 2 вопросов будет состоять из подготовленных вопросов. Решение. Задача №14. Из 30 карточек с буквами русского алфавита наудачу выбирают 4 карточки. Чему равна вероятность того, что эти 4 карточки в порядке выхода составят слово "небо"? Решение. Задача №15. На полке расставлено наудачу 10 книг. Определить вероятность того, что 3 определённые книги окажутся рядом. Решение. Пояснение. При вычислении m три указанные книги принимаем за одну. Задача №16. В лотерее 1000 билетов. Из них 500 выигрывают, 500 проигрывают. Куплено 2 билета. Найти вероятность того, что оба билета выиграют. Решение. Пусть случайное событие А={2 билета выигрывают}, тогда: Задача №17. Наудачу выбирается 5-тизначное число. Какова вероятность события: А = {число симметрично относительно центральной цифры}; В = {число кратно 5}; С = {число состоит из нечётных цифр}. Решение. Всего пятизначных чисел: Задача №18. В коробке 15 одинаковых изделий, 5 из них окрашены. Наугад извлекают 3 изделия. Найти вероятность того, что a) все 3 изделия окрашены; b) одно изделие окрашено. Решение. Рассмотрим события: А1 = {все 3 изделия окрашены}; А2 = {из всех 3 изделий только 1 окрашено}. Задача №19. Среди 12-ти студентов, 7 из которых девушки, раздают 5 билетов. Найти вероятность того, что среди обладателей билетов будут 3 девушки (событие А). Решение. Задача №20. Из колоды карт (36 штук) наудачу извлекают 3 карты. Найти вероятность того, что среди них окажется туз. Решение. Задача №21. Из 10 изделий, из которых 3 бракованные, наудачу извлекают три изделия для контроля. Найти вероятность того, что: a)в полученной выборке все изделия бракованные; b)в полученной выборке 2 изделия бракованные. Решение. А={в полученной выборке все изделия бракованные}; B={в полученной выборке 2 изделия бракованные}; Задача №22. Дано пять отрезков, длины которых составляют соответственно 1, 3, 5, 7, 9. Определить вероятность того, что из взятых наудачу 3-х отрезков из данных пяти можно построить треугольник (событие А). Решение. Всего отобрать 3 отрезка из заданных 5-ти можно Задача №23. Кандидаты в студенческий совет: 3 – от I-го курса, 5 – от II-го, 7 – от III-го. Выбираются наудачу 5 человек на конференцию. Найти вероятность того, что делегация будет состоять из 1-го первокурсника, 2-х второкурсников, 2-х третьекурсников. Решение. Пусть А = {делегация состоит из 1-го первокурсника, 2-х второкурсников, 2-х третьекурсников}. Тогда: Задача №24. Наугад выбирают 6 клеток из 49 (спортлото). Найти вероятность того, что будет правильно угадано 3 клетки (событие А), 6 клеток (событие В). Решение. Раздел 3. Алгебра событий Исходя из определения суммы и произведения событий, совместных и несовместных событий, зависимых и независимых событий, основных теорем алгебры событий (1),(2) запишем основные формулы, связанные с ними. Пусть рассматриваются события А и В, которые могут произойти в данном эксперименте с вероятностью Р(А) и Р(В) соответственно. Если эти события несовместны, то имеет место формула: Р(А+В)=Р(А)+Р(В). (3.1) Если события А и В совместные, то: Р(А+В)=Р(А)+Р(В)-Р(АВ). (3.2) Если события А и В независимые, то: в противном случае Здесь Р(В/А) и Р(А/В) – условные вероятности. Задачи Задача №25. Вероятность попадания стрелком в I-ю область мишени равна 0,45, во II-ю – 0,35, в III-ю – 0,15. Найти вероятность того, что при одном выстреле стрелок попадёт в I-ю или во II-ю область мишени (рис.2). Рис.2 Решение. Пусть: А1 ={попадание в I-ю область}, А2 ={попадание во II-ю область}. События А1и А2 несовместны при одном выстреле. Поэтому Задача №26. Из 10 тыс. лотерейных билетов: 10 – по 200 грн., 100 – по 100 грн., 500 – по 25 грн., 1000 – по 5 грн. выигрыша. Найти вероятность того, что купленный билет будет содержать выигрыш не менее 25 грн. Решение. Пусть события: А = {выигрыш в случайно купленном билете не менее 25 грн.}; А1 ={выигрыш составил 25 грн.}; А2 ={выигрыш составил 100 грн.}; А3 ={выигрыш составил 200 грн.}; Тогда вероятность выигрыша 25 грн. Очевидно, что событие А представляет собой сумму событий А1, А2, А3, несовместных между собой, поэтому: Р(А) = Р(А1) + Р(А2) + Р(А3) = 0,061. Задача №27. В первом ящике 2 белых и 10 чёрных шаров. Во втором ящике 8 белых и 4 чёрных шара. Из каждого вынули по шару. Найти вероятность того, что оба шара белые. Решение. Пусть: А={белый шар из 1го ящика}; В={белый шар из 2го ящика}. Тогда: События A и В независимы Задача №28. Три стрелка стреляют по цели. Вероятность попадания для 1-го стрелка (событие А) равна 0,75, для 2-го (событие В) – 0,8, для 3-го (событие С) – 0,9. Определить вероятность того, что все три стрелка одновременно попадут в цель (событие D). Решение. События A, B, C – независимы Задача №29. В условиях задачи №28 найти вероятность того, что в цель попадёт хотя бы один стрелок (событие R). Решение. Найдём вероятность того, что в цель не попадёт ни один стрелок (событие Т.к. Задача №30. Найти вероятность попадания стрелком в цель при одном выстреле (событие В), если вероятность события А={хотя бы одно попадание в цель при 4-х выстрелах}=0,9984 Вероятность непопадания при одном выстреле равна: Окончательно получаем: Задача №31. Студент обходит 3 библиотеки. Вероятность того, что книга есть в каждой из 3-х библиотек равна р1, вероятность того, что имеющаяся книга не выдана, равна р2. Какова вероятность того, что студент достанет книгу хотя бы в одной из библиотек. Решение. А1 = {достанет книгу в 1-ой библиотеке}; А2 = {достанет книгу во 2-ой библиотеке}; А3 = {достанет книгу в 3-й библиотеке}; В1 = {книга есть}; В2 = {книга не выдана}; Задача №32. Охотник выстрелил 3 раза по удалённой цели. Вероятность попадания в цель в начале стрельбы равна 0,8. Вероятность попадания в цель после каждого выстрела уменьшается на 0,1. Найти вероятность попадания в цель 2 раза (событие D). Решение. Пусть A= {попадание в цель при 1-ом выстреле}; B= {попадание в цель при 2-ом выстреле}; C={попадание в цель при 3-ем выстреле}. Тогда P {A} = 0,8; P {B} = 0,7; P {С} = 0,6. Задача №33. Вероятность того, что первый из 3-х человек придет, равна 0,8. Вероятность того, что второй придет, равна 0,4. Вероятность того, что придёт третий, равна 0,7. Найти вероятность того, что встреча состоится, если для этого нужно, чтобы пришли хотя бы двое из трёх. Решение. Пусть A={придёт первый}; B={придёт второй}; C={придёт третий}; Тогда: Ответ: 0,488. Задача №34. В зависимости от наличия сырья предприятие может отправить заказчикам в сутки определённое количество продукции от 1 до 100 ед. Найти вероятность того, что полученное количество продукции можно распределить без остатка: a) 3-м заказчикам (событие А); b) 4-м заказчикам (событие В); c) 12-ти заказчикам (событие С); d) 3-м или 4-м заказчикам (событие D). Решение. C=A События А и В совместные Задача №35. Рабочий обслуживает 2 станка. В течение 8-ми часов каждый из станков приостанавливается по разным причинам. Получасовые остановки равновероятны. Найти вероятность того, что в данный момент времени только 1 станок работает. Найти вероятность того, что работают оба станка. Решение. С={в данный момент работает только один станок}; D={в данный момент работают оба станка}; A1={работает первый станок}; A2={работает второй станок}. Задача №36. В читальном зале 6 учебников по теории вероятностей (т.в.). Из них 3 – в переплете. Библиотекарь наудачу взял 2 учебника. Найти вероятность того, что оба учебника в переплете. Решение. Пусть события: A= {I-ый учебник в переплете} B={II-ой учебник в переплете} С={оба учебника в переплете}. Тогда: Иначе: Задача №37. В ящике детали 3-х сортов: 5 – I-го сорта, 4 – II-го, 3 – III-го. Из ящика наудачу извлекается 1 деталь и не возвращается в ящик. Найти вероятность того, что при первом испытании появится деталь I-го сорта (событие А), при втором испытании – II-го сорта (событие В), при третьем – третьего сорта (событие С). Решение. Задача №38. Вероятность попадания в 1-ю мишень (событие А) для данного стрелка равно 2/3. Если стрелок попал в первый раз, то он получает право на второй выстрел по другой мишени. Вероятность поражения обеих мишеней при 2-х выстрелах равна 0,5. Найти вероятность поражения второй мишени. Решение. Пусть: А={поражение 1-й мишени}; В={поражение 2-й мишени}; С={поражение обеих мишеней}. По условию, Задача №39. 4% всей продукции – брак. 75% небракованных изделий удовлетворяют требованиям первого сорта. Найти вероятность того, что выбранное изделие первого сорта. Решение. Пусть: A={изделие первого сорта}; В={изделие небракованное}; Тогда: Задача №40. Абонент набирает наугад последнюю цифру телефона. Определите вероятность того, что: a) В1 ={придется звонить не более 3-x раз}; b) В2 ={то же, но при условии, что неизвестная цифра нечётная}. Решение. А1 ={в 1 раз набрал нужную цифру}; А2 ={во 2-й раз набрал нужную цифру}; А3 ={в 3-й раз набрал нужную цифру}. Вероятность того, что за 3 раза он не набрал нужную цифру, равна: Вероятность того, что в течение этих 3-х раз набрал хотя бы один раз нужную цифру, равна: При условии, что набираемая цифра нечётная, имеем: Задача №41. В лотерее имеются 10 билетов, из них 5 билетов стоимостью по 1 грн, 3 билета – по 3 грн, 2 билета – по 5 грн. Наудачу берут 3 билета. Найти вероятность того, что хотя бы 2 из этих билетов имеют одинаковую стоимость. Решение. Всего способов выбрать 3 билета из 10-ти Обозначим A={все 3 билета разные}. Событие Задача №42. Спортсмены на соревнованиях делают 1 упражнение с 3-х попыток. Вероятность успешного выполнения 1-й попытки равна 0,8. Вероятность успешного выполнения 2-й попытки равна 0,7. Вероятность успешного выполнения 3-й попытки равна 0,4. Найти вероятность того, что спортсмен успешно выполнить это упражнение (событие А). Решение. А1 = {успех в 1-й попытке}; А2 = {успех во 2-й попытке}; А3 = {успех в 3-й попытке}. Иначе: Задача №43. 68% мужчин, достигших 60-летия, достигают и 70-летия. Найти вероятность того, что 60-летний мужчина не достигнет своего 70-летия. Решение. Пусть: событие А={60-летний мужчина достигнет своего 70- летия}, тогда: Р( Задача №44. В лотерее n билетов, из которых m – выигрышные. Вы приобрели k билетов. Найти вероятность того, что: а) среди k билетов ровно l выигрышные (событие А); б) среди k билетов хотя бы 1 выигрышный (событие В). Решение. а) б) вероятность того, что среди k билетов хотя бы один выигрышный, равна: Задача №45. В некотором обществе 70% людей – курят, 40% – с больными лёгкими, 25% – и курят, и болеют. Найти вероятность того, что наудачу взятый человек из этого общества: a) не курит, но с больными лёгкими; b) курит, но не болеет; c) не курит и не болеет; d) курит и болеет; e) или курит, или болеет. Решение. Пусть А={человек курит}; В={человек с больными лёгкими}. Тогда: P(A)=0,7; P(B)=0,4; P( Имеем: а) b) c) d) e) Задача №46 (о легкомысленном члене жюри). В жюри из 3-х человек 2 члена независимо друг от друга принимают правильное решение с вероятностью р, а третий для вынесения решения бросает монету. Окончательное решение выносится большинством голосов. Жюри из одного человека выносит справедливое решение с вероятностью р. Какое из этих жюри вынесет справедливое решение с большей вероятностью? 2р(1-р) Вывод: Оба типа жюри имеют одинаковую вероятность вынести справедливое решение. Раздел 4. Основные теоремы теории вероятности 4.1 Формула полной вероятности Группа гипотез – полная группа несовместных событий (пусть это будет Н1, Н2 , …, Нn). Пусть событие А может наступить лишь при появлении одного из них. Тогда вероятность события А вычисляется по формуле: которая называется формулой полной вероятности. Здесь: Задачи Задача №47. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнения квалификационной нормы равна: для лыжников – 0,9, для велосипедистов – 0,8, для бегунов – 0,75. Найти вероятность того, что спортсмен, вызванный наудачу, выполнит норму. Решение. А = {спортсмен выполнил норму}; Н1 = {выполнил лыжник}; Н2 = {выполнил велосипедист}; Н3 = {выполнил бегун}. Задача №48. Стрельба производилась по 3-м мишеням. По 1-ой – 5 раз, по 2-ой – 3 раза, по 3-ей – 2 раза. Вероятность попадания по 1-ой мишени равна 0,4, по 2-ой мишени – 0,1, по 3-ей – 0,12. Найти вероятность одного попадания в мишень. Решение. Пусть A = {попадание в мишень при одном выстреле} H1 = {стреляли в 1-ю мишень} P(H1) = 0,5 H2 = {стреляли в 2-ю мишень} P(H2) = 0,3 H3 = {стреляли в 3-ю мишень} P(H3) = 0,2 P(A/H1) = 0,4 P(A/H2) = 0,1P(A/H3) = 0,12 Задача №49. В лаборатории 3 одинаковых клетки. В 1-й - 3 белых и 7 коричневых мыши, во 2-й – 5 белых и 6 коричневых. В 3-й – 7 белых и 2 коричневых. Случайным образом берут из одной клетки мышь. Найти вероятность того, что выбрана белая мышь (событие А). Решение. Пусть имеется 3 гипотезы: Н1 = {выбрана мышь из 1-й клетки}; Н2 = {выбрана мышь из 2-й клетки}; Н3 = {выбрана мышь из 3-й клетки}; Р(Н1)= Р(Н2)= Р(Н3)=1/3 Условные вероятности события А будут равны: Р(А/Н1)= 3/10; Р(А/Н2)=5/11; Р(А/Н3)=7/9. По формуле (4.1) имеем: Задача №50. Судостроительный завод получает от 3-х предприятий детали: от предприятия В – 60%, от С – 30%, от D – 10%. При этом на каждом из этих предприятий допускается брак, соответственно на В – 4%, на С – 5%, и на D – 6%. Какова вероятность того, что случайно выбранная деталь будет бракованной (событие А), если известно, от какого предприятия она поступила. Решение. В качестве гипотез событий примем: Н1 = {деталь поступила от предприятия В}; Н2 = {деталь поступила от предприятия С}; Н3 = {деталь поступила от предприятия D}. Р(Н1) = 0,6; Р(Н2) = 0,3; Р(Н3) = 0,1 Условные вероятности события А равны соответственно: Р(А/Н1)= 0,04;Р(А/Н2)=0,05;Р(А/Н3)=0,06. По формуле (4.1) имеем: Задача №51. В магазин поступили телевизоры от 5-ти фирм в следующем количестве: Рi Рi – вероятности того, что телевизоры исправны. Найти вероятности того, что купленный наугад телевизор исправно работает (событие А) Решение. 1) В качестве гипотез выберем события: 2) Найдём вероятности гипотез, учитывая, что п=40: Р(Н1) = 5/40; Р(Н2) = 10/40; Р(Н3) = 6/40; Р(Н4) = 8/40; Р(Н5) = 11/40. 3) Условные вероятности равны: Р(А/Н1) = 0,98; Р(А/Н2) = 0,8; Р(А/Н3) = 0,6; Р(А/Н4) = 0,3; Р(А/Н5) = 0,1. 4) По формуле (4.1) имеем: Задача №52. Имеются 3 одинаковых ящика, в каждом из которых по 20 однотипных деталей. Определить вероятность того, что извлечённая из наугад выбранного ящика деталь стандартная (событие А), если известно, что в 1-м ящике 18 стандартных деталей, во 2-м – 17, в 3-м – 16. Решение. Если в качестве i-й гипотезы (i = 1,2,3) выбрать событие Нi = {деталь из i-го ящика}, то Р(Нi) =1/3. Р(А/Н1) = 18/20; Р(А/Н2) = 17/20; Р(А/Н3) = 16/20. По формуле (4.1) имеем: 4.2 Формула Байеса (формула переоценки вероятности гипотез) Пусть событие А может наступить лишь при условии появления одной из гипотез Задачи Задача №53. 70% населения обследуемого региона имеет только среднее образование, среди которых 10% безработных, 30% населения – с высшим образованием, среди них 2% безработных. Если выбранный наугад человек является безработным, то какова вероятность того, что он закончил ВУЗ? Решение. В качестве гипотезы примем: Н1 = {выбранный наугад человек со средним образованием}; Н2 = { выбранный наугад человек со высшим образованием }. Р(Н1) = 0,7; Р(Н2) = 0,3. Пусть соб. А = {выбранный наудачу человек безработный}, тогда P(A/H1) = 0,1, P(A/H2) = 0,02. Нужно определить P( Имеем: Задача №54. На сборочный конвейер поступили детали с 3-х станков, производительность которых неодинакова: I-го – 50% плана, II-го – 30% плана, III-го – 20% плана. Вероятность получения годного узла равна 0,92, если деталь I-го станка, 0,95,если деталь со II-го станка, 0,82, если деталь с III-го станка. Определить вероятность того, что в сборку попали детали, изготовленные на первом станке, если узел годный. Решение. А = { узел годный}; Н1 = {деталь с I-го станка}; Н2 = {деталь со II-го станка}; Н3 = {деталь с III-го станка}; Р(Н1)=0,5; Р(Н2)=0,3; Р(Н3)=0,2. Р(А/Н1)=0,92; Р(А/Н2)=0,95; Р(А/Н3)=0,82. Задача №55. 30% приборов собирают специалисты высокой квалификации, 70% - средней квалификации. Надёжность работы прибора, собранного специалистом высокой квалификации – 0,9, а специалистом средней квалификации – 0,8. Взятый наугад прибор оказался надёжным. Определить вероятность того, что прибор собран специалистом высокой квалификации. Решение. Пусть событие А = {прибор работает безотказно}. До проверки прибора возможны 2 гипотезы: Н1 = {прибор собран специалистом высокой квалификации}; Н2 = { прибор собран специалистом средней квалификации }. Р(Н1) = 0,3, Р(Н2) = 0,7. Условные вероятности события А равны: P(A/H1) = 0,9, P(A/H2) = 0,8. Пусть событие А произошло, тогда Задача №56. Из 10 учащихся, которые пришли на экзамен по математике (нужно было подготовить 20 вопросов), трое подготовились на отлично (выучив по 20 вопросов), четверо – на хорошо, выучив по 16 вопросов, двое – на удовлетворительно, выучив по 10 вопросов, один не готовился и может ответить на 5 вопросов из 20. В билете 3 вопроса. Первый ученик ответил на все 3 вопроса своего билета. Какова вероятность того, что этот ученик подготовился на отлично? Решение. Пусть событие А = {1-й ученик ответил на 3 вопроса} и гипотезы: Н1 = {1-й ученик подготовлен на 5}; Н2 = {1-й ученик подготовлен на 4}; Н3 = {1-й ученик подготовлен на 3}; Н4 = {1-й ученик подготовлен на 2}. P(H1) = 0,3; P(H2) = 0,4; P(H3) = 0,2; P(H4) = 0,1 P(А/H1) = 1 (событие {1-й ученик ответил на 3 вопроса, при условии, что он выучил 20 из 20}, является достоверным). По формуле (4.2) имеем: Вывод: учителю придётся предложить ученику ещё дополнительные вопросы. Раздел 5. Случайные величины (с.в.) 5.1 Дискретные случайные величины Дискретной случайной величиной называют случайную величину, возможные значения которой есть изолированные числа (число их может быть конечным или бесконечным для счетного множества). При этом название закона распределения диктует формула, по которой вычисляются вероятности, соответствующие возможным значениям С.В. Ниже приведены наиболее часто встречающиеся на практике: - биномиальный закон распределения дискретной с.в. X – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна p. Вероятность возможного значения Х= k по формуле Бернулли равна: - если n велико, а p в каждом испытании очень мало, то используется приближённая формула (распределение Пуассона): Здесь - если вероятность появления события А в каждом испытании p ( Ряд вероятностей этого распределения будет бесконечной геометрической прогрессией со знаменателем q<1 и суммой, равной единице. Такое распределение называется геометрическим; - в задачах статистического контроля качества часто используется гипергеометрический закон распределения дискретной с.в. При этом применяется формула: Здесь из совокупности n элементов, которая содержит m элементов определённого свойства (напр., среди n деталей ровно m бракованных), отбираются случайным образом k элементов. P(X=l) – это вероятность того, что среди k отобранных элементов ровно l элементов с определённым свойством. - Кроме указанных законов распределения, на практике используются числовые характеристики с.в.: - математическое ожидание M(X); - дисперсия D(X); - среднее квадратическое отклонение Для биномиального распределения (формула (5.1)) имеем: M(X)=np (5.9) D(X)=npq (5.10) Для распределения Пуассона (формула (5.2)): M(Х)=D(Х)=np= Задачи Задача №57. В партии из 6-ти деталей 4 стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной с.в. Х
![]()
![]() (arrangement(фр.) - размещение) и вычисляется по формуле:
(arrangement(фр.) - размещение) и вычисляется по формуле:![]()
![]()
![]() (1.2)
(1.2)![]()
![]()
![]()
![]() и т.д.
и т.д.![]() (combinare (лат.) - соединять).
(combinare (лат.) - соединять).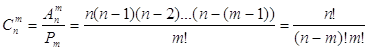 (1.3)
(1.3)![]()
![]() Используя основное свойство числа сочетаний
Используя основное свойство числа сочетаний ![]() , мы упростим вычисления
, мы упростим вычисления![]() .
.![]() .
.![]()
![]() (правило произведения).
(правило произведения).![]() .
.![]() .
.![]() .
.![]()
![]() . Аналогично из 20 девочек:
. Аналогично из 20 девочек: ![]() . Общее число способов выбора дуэтов певцов, танцоров и декламаторов по правилу произведения равно
. Общее число способов выбора дуэтов певцов, танцоров и декламаторов по правилу произведения равно ![]() способов.
способов.![]() .
.![]() .
.Ξ Ξ Ξ Ξ Ξ Ξ Ξ Ξ ![]()
![]()
![]() (2.1)
(2.1)![]() .
.![]()
![]() .
.![]() вероятность угадать расписание:
вероятность угадать расписание:![]() .
.![]() . Из них только
. Из них только ![]() карточек благоприятствуют событию А, т.к. только 5 чисел 2, 4, 6, 8, 12 сократимы Þ
карточек благоприятствуют событию А, т.к. только 5 чисел 2, 4, 6, 8, 12 сократимы Þ ![]() .
. .
.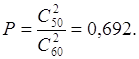
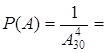
![]()
![]() 15
15![]() .
.![]() .
.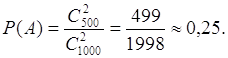
![]() (правило произведения).
(правило произведения).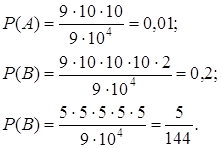
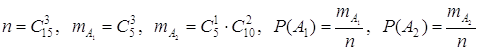
![]()
![]()
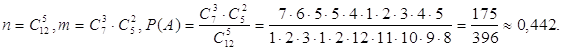
![]() .
.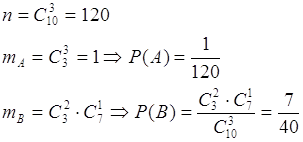 .
.![]() вариантами, т.е.
вариантами, т.е. ![]() ; благоприятных (a
; благоприятных (a![]() b>c или a-b
b>c или a-b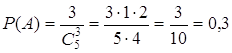 .
.![]()
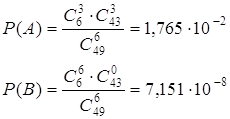
![]() , (3.3)
, (3.3)![]() (3.4)
(3.4)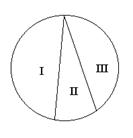
![]()
![]() .
.Аналогично,
![]()
![]()
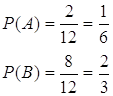
![]()
![]() .
.![]()
![]()
![]() ).
).![]() - событие, противоположенное событию R, оно равно
- событие, противоположенное событию R, оно равно ![]()
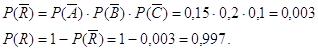
Решение
![]() =0,9984,
=0,9984, ![]() = {ни одного попадания в цель при 4-х выстрелах}
= {ни одного попадания в цель при 4-х выстрелах} ![]()
![]()
![]() =
= ![]()
![]() = {не достанет ни в одной библиотеке}.
= {не достанет ни в одной библиотеке}.![]() – вероятность того, что студент достанет книгу хотя бы в одной библиотеке.
– вероятность того, что студент достанет книгу хотя бы в одной библиотеке.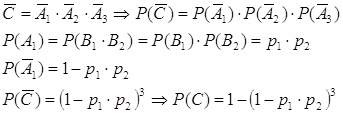
![]()
![]() .
. D={придут хотя бы двое из трёх}.
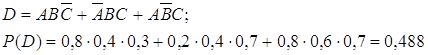
![]()
![]()
![]()
![]() B, D=A
B, D=A![]() B.
B.![]()
![]()
![]()
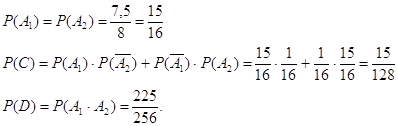
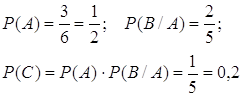
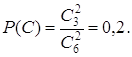
![]() (всего деталей 12)
(всего деталей 12)![]()
![]()
![]() , но т.к. А и В – события зависимые, то:
, но т.к. А и В – события зависимые, то: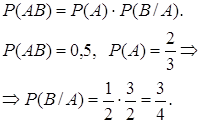
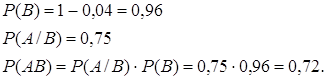
![]()
![]()
![]()
![]() .
.Тогда:
![]()
![]() {хотя бы 2 билета одинаковой стоимости} является противоположным событию А, поэтому:
{хотя бы 2 билета одинаковой стоимости} является противоположным событию А, поэтому:![]()
![]()
![]()
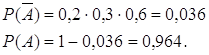
![]() {60-летний мужчина не достигнет своего 70-летия}.
{60-летний мужчина не достигнет своего 70-летия}.![]() )
)![]() Р(А)=
Р(А)=![]() =0,32.
=0,32.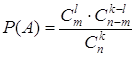
![]() {среди k билетов ни одного выигрышного}
{среди k билетов ни одного выигрышного}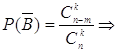
![]()
![]() =0,25.
=0,25.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Решение. Пусть оба (из 3-х) членов жюри сходятся во мнениях, тогда вероятность справедливого решения равна
Решение. Пусть оба (из 3-х) членов жюри сходятся во мнениях, тогда вероятность справедливого решения равна ![]() . При этом результат голосования 3-го жюри несущественен. Если судьи расходятся во мнениях, то вероятность справедливого решения 2-х судей –
. При этом результат голосования 3-го жюри несущественен. Если судьи расходятся во мнениях, то вероятность справедливого решения 2-х судей – ![]() . Полная вероятность вынесения справедливого решения жюри из 3х членов равна:
. Полная вероятность вынесения справедливого решения жюри из 3х членов равна:![]() р2
р2![]() р-р2
р-р2![]() р.
р.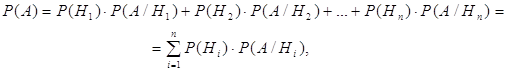 (4.1)
(4.1)![]() - вероятности гипотез;
- вероятности гипотез;![]() -условные вероятности события А.
-условные вероятности события А.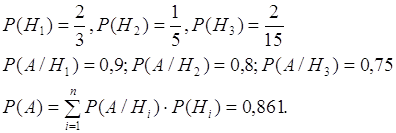
![]() По формуле (4.1) имеем:
По формуле (4.1) имеем: ![]() .
.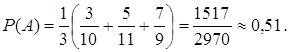
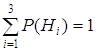
![]()
Фирма 1 2 3 4 5 Количество телевизоров 5 10 6 8 11 0,98 0,8 0,6 0,3 0,1 ![]() {телевизор i-й фирмы}, (i=
{телевизор i-й фирмы}, (i=![]() ).
).![]()
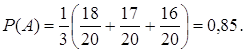
![]() (см п.4.1). Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса:
(см п.4.1). Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса: 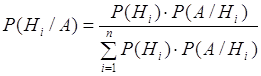 (4.2)
(4.2)![]() ) по формуле (4.2).
) по формуле (4.2).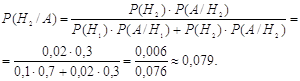
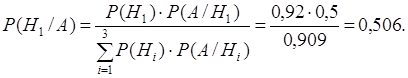
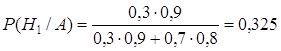 .
.![]() (вероятность правильного ответа на 1-й вопрос равна 16/20, на 2-й – 15/19, на 3-й – 14/18).
(вероятность правильного ответа на 1-й вопрос равна 16/20, на 2-й – 15/19, на 3-й – 14/18).![]()
![]()
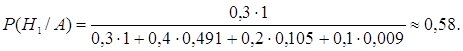
![]() Зависимость вероятностей от возможных значений с.в. есть закон распределения дискретной с.в., который может быть представлен в виде ряда распределения, многоугольника распределения, функции распределения с.в.
Зависимость вероятностей от возможных значений с.в. есть закон распределения дискретной с.в., который может быть представлен в виде ряда распределения, многоугольника распределения, функции распределения с.в.![]() (5.1)
(5.1) ,
, ![]() np (5.2)
np (5.2)![]() .
.![]() ), а Х – число испытаний до появления события А в серии независимых повторных испытаний, то пользуются формулой:
), а Х – число испытаний до появления события А в серии независимых повторных испытаний, то пользуются формулой: ![]() (5.3)
(5.3)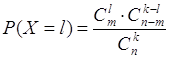 (5.4)
(5.4) ![]() X).
X).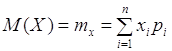 (5.5)
(5.5)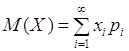 (5.6)
(5.6)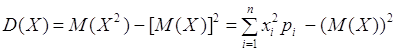 (5.7)
(5.7)![]() (5.8)
(5.8)![]() (5.11)
(5.11)