Логика. Суждение. Умозаключение
ПЛАН:
1. Логика как наука……………………………………………………………..3
а) Предмет и законы логики……………………………………………..............3
б) Понятие логической формы. Логические категории и символы……………5
2. Понятие как форма мысли…………………………………………………..7
а) Понятие как форма мысли. Логическая характеристика понятий…………..7
б) Соотношение между понятиями по объему………………………………….7
в) Деление понятий. Правила и виды делений………………………………….8
г) Обобщение и ограничение понятий………………………………………...10
3. Суждение как форма мысли………………………………………………11
а) Виды и структура суждений…………………………………………………11
б) Классификация простых атрибутивных суждений по количеству и качеству……………………………………………………………......................12
в) Распределенность терминов в простом атрибутивном суждении………....13
г) Правила вывода из суждений по логическому квадрату………….............15
4. Умозаключение как форма мысли………………………………………..16
а) Понятие и виды умозаключений……………………………………………..16
б) Простой категорический силлогизм: правила, фигуры и модусы…………18
в) Условное и разделительно – категорическое умозаключение……………..20
г) Условно – категорическое умозаключение: правильные и неправильные модусы…………………………………………………………………………....21
д) Условно – разделительное умозаключение. Сложные и простые модусы………………………………………………………………………..…..23
е) Сокращенный силлогизм…………………………………………………….24
ж) Индуктивные умозаключения. Виды индукции…………………………..26
з) Умозаключения по аналогии………………………………………………..27
СПИСОК ЛИТЕРАТУРЫ………………………………………………….…..28
1. Логика как наука
а) Предмет и законы логики
Логика - это наука об общезначимых формах и средствах мысли, необходимых для рационального познания в любой области.
Следовательно, предмет логики составляют:
1. Законы, которым подчиняется мышление в процессе познания
объективного мира.
2. Формы мыслительного процесса - понятия, суждения и умозаключения.
3. Методы получения нового выводного знания - сходства, различия
сопутствующих изменений, остатков и другие.
4. Способы доказательства истинности полученных знаний: прямое и
косвенное доказательство, опровержение и так далее.
Итак, логика (в наиболее широком понимании ее предмета) исследует структуру мышления, раскрывает лежащие в его основе закономерности. При этом абстрактное мышление, обобщенно, опосредствованно и активно отражая действительность, неразрывно связано с языком. Языковые выражения являются той реальностью, строение и способ употребления которой дает нам знание не только о содержании мыслей, но и об их формах, о законах мышления. Поэтому в исследовании языковых выражений и отношений между ними логика видит одну из своих основных задач. А язык в целом является при этом косвенным объектом ее внимания и интереса.
Логические законы.
1) Закон тождества.
Самый простой из всех логических законов – это, пожалуй, закон тождества. Он говорит: если утверждение истинно, то оно истинно, «если А, то А». Он утверждает только, что если вещь меняется, то она меняется, а если она остается одной и той же, то она остается той же.
2) Закон противоречия.
Закон противоречия говорит о противоречащих друг другу высказываниях, то есть о таких высказываниях, одно из которых является отрицанием другого. В одном из противоречащих высказываний что-то утверждается, в другом – это же самое отрицается.
Если обозначить буквой А произвольное высказывание, то выражение не-А, будет отрицанием этого высказывания.
Идея, выражаемая законом противоречия, кажется простой и даже банальной: высказывание и его отрицание не могут быть вместе истинными.
Закон противоречия говорит о противоречащих высказываниях – отсюда его название. Но он отрицает противоречие, объявляет его ошибкой и тем самым требует непротиворечивости – отсюда другое распространенное имя – закон непротиворечия.
3) Закон исключенного третьего
Закон исключительного третьего, как и закон противоречия, устанавливает связь между противоречащими друг другу высказываниями. И опять-таки идея, выражаемая им, представляется поначалу простой и очевидной: из двух противоречащих высказываний одно является истинным.
Истинность отрицания равнозначна ложности утверждения. В силу этого закон исключенного третьего можно передать и так: каждое высказывание является истинным или ложным.
Само название закона выражает его смысл: дело обстоит так, как описывается в рассматриваемом высказывании, иди так, как говорит его отрицание, и никакой третьей возможности нет.
4) Закон достаточного основания.
Четвертый основной закон формальной логики выражает то фундаментальное свойство логической мысли, которое называют обоснованностью или доказанностью. Формулируется он обычно так: всякая мысль истинна или ложна не сама по себе, а в силу достаточного основания. Это значит: любое положение, прежде чем стать научной истиной, должно быть подтверждено аргументами, достаточными для признания его твердо и неопровержимо доказанным. Закон достаточного основания был введен, как уже отмечалось, Лейбницем и не сразу получил признание логиков.
б) Понятие логической формы. Логические категории и символы
Формальная логика - наука о законах и формах правильного мышления. Логической формой конкретной мысли является строение этой мысли, то есть способ связи ее составных частей. Понятия, суждения, умозаключения имеют свои специфические формы (структуры).
Формальная логика в своем развитии прошла два основных этапа.
Начало первого этапа связано с работами древнегреческого философа и ученого Аристотеля (384 - 322 до н.э.), который впервые дал систематическое изложение логики.
Традиционная формальная логика включает разделы, понятие, суждение, умозаключение, законы логики, доказательства и опровержение, гипотеза. Основным содержанием аристотелевой логики является теория дедукции.
Вторым составляющим первого этапа является логика стоиков (античная философская школа, 3 в. до н.э.). В стоитской логике таковыми выступают развернутые суждения, обозначающие смысл ситуаций или развернутых фактов.
Новый, более высокий этап в развитии логики, начинается с 17 века. В рамках наряду с дедуктивной логикой логики индуктивной. Ее родоначальником стал Фрэнсис Бэкон.
Позднее она была систематизирована и развита английским философом Джоном Стюартом Миллем.
Категория (от греч. kategoria - высказывание, обвинение, признак) – предельно общее фундаментальное понятие, отражающее наиболее существенные, закономерные связи и отношения реальной действительности и познания. Будучи формами и устойчивыми организующими принципами процесса мышления, категории воспроизводят свойства и отношения бытия и познания во всеобщем и наиболее концентрированном виде. Характеристику некоторых особенностей категорий можно дать, опираясь на операцию обобщения понятий. К категориям относятся предельно широкие по своему объему понятия, то есть те, для которых нельзя найти более широкие родовые понятия. Как правило, категории являются философские понятия – «бытие», «субъект», «сущность», «качество», «количество», «материя», «сознание» и тому подобное. В каждой конкретной науке имеется своя система категорий. В логике к числу наиболее общих и фундаментальных понятий относятся понятия логического вывода, суждения, умозаключения, индукции, дедукции и другие. Категории изменяются вместе с развитием нашего познания: обогащается их содержание, изменяются взаимосвязи между категориями, меняется их состав и тому подобное.
Символ (от греч. symbolon – знак, опознавательная примета) - идея, образ или объект, имеющий собственное содержание и одновременно представляющий в обобщенной, неразвернутой форме некоторое иное содержание. Символ стоит между (чистым) знаком, у которого собственное содержание ничтожно, и моделью, имеющей прямое сходство с моделируемым объектом, что позволяет модели замещать последний в процессе исследования. Символ используется человеком в некоторых видах деятельности и имеет в силу этого определенную цель. Он всегда служит обнаружению чего-то неявного, не лежащего на поверхности, непредсказуемого. Если цель отсутствует, то нет и символа как элемента социальной жизни, а есть то, что обычно называется знаком и служит для простого обозначения объекта. Роль символа в человеческой практике и познании мира невозможно переоценить. Разъяснение смысла символа неизбежно ведет к новым символам; которые не только не способны исчерпать всю его глубину, но и сами требуют разъяснения.
2. Понятие как форма мысли
а) Понятие как форма мысли. Логическая характеристика понятий
Понятие как форма мышления отражает предметы и их совокупность в абстрактной, обобщенной форме на основании их существенных признаков.
Понятие – одна из основных форм научного познания. Формируя понятие, наука отражает в них изучаемые ею предметы, явления, процессы.
Кроме единичных (индивидуальных) и общих признаков логика выделяет признаки существенные и несущественные.
Признаки, необходимо принадлежащие предмету, выражающие его сущность, называют существенными. Они могут быть общими и единичными. Понятия, отражающие множество предметов, включают общие существенные признаки (напр. способность создавать орудие труда). Понятие, отражающее один предмет (напр. «Аристотель»), наряду с общими существенными признаками (человек, древнегреческий философ) включает единичные признаки.
Признаки, которые могут принадлежать, но могут и не принадлежать предмету и которые не выражают его сущность, называются несущественными.
Понятие качественно отличается от форм чувственного познания: ощущений, восприятия и представлений, существующих в сознание человека в виде наглядных образов отдельных предметов или их свойств. Восприятие и представление – это чувственно-наглядный образ какого-либо конкретного предмета. Понятие лишено наглядности.
Отражая существенное, понятия не содержат всего богатства индивидуальных признаков предмета и в этом смысле они беднее форм чувственного познания – восприятия и представления. Вместе с тем, они позволяют глубже проникнуть в действительность, отобразить её с большей полнотой, на что не способно чувственное познание.
б) Соотношение между понятиями по объему
Предмет, о котором известно только то, что он подходит под то или иное понятие, и больше ничего, есть целиком мыслительное образование и называется абстрактным предметом. Совокупность абстрактных предметов, соответствующих одному и тому же понятию, составляет его объем.
Множество предметов, которое мыслится в понятии, называется объемом понятия.
Объем понятия, составляют все другие понятия, для которых оно является общим. Например, понятие машины является общим для таких понятий, как автомобиль, грейдер, экскаватор и так далее. Такой объем можно было бы назвать объемом разнообразия, потому что он показывает, как велико число разновидностей данного явления, как разнообразно оно: объем понятия – все предметы, к которым относится данное понятие.
Объём понятия не может состоять из реальных предметов, а может состоять лишь из мыслей. объем понятия составляют утверждения о наличии (существовании) конкретных предметов (или их категорий, понимаемых как одно целое), которые обладают свойствами, подходящими под данное понятие, что позволяет быть реальным и данному понятию. Объемы, составленные из утверждений о существовании предметов, соответствующих данному понятию; могут быть названы количественными.
При обращении с объемами понятий возможна следующая ошибка: части предмета могут полагаться частями объёма. Получается сколько у предмета частей, таков и его объем. Но части предмета – это не экземпляры, не категории и разновидности предмета. Плавник не есть разновидность рыбы, потому объемы этих двух понятий не соприкасаются.
в) Деление понятий. Правила и виды делений
При изучении какого-либо понятия нередко встает задача раскрыть его объем, то есть распределить предметы, которые мыслятся в понятии, на отдельные группы. Логическая операция, раскрывающая объем понятия, называется делением.
Различают деление:
1) Деление по видоизменению признака.
Основанием деления является признак, при изменении которого образуются видовые понятия, входящие в объем делимого (родового) понятия. Например, государства в зависимости от формы государственного устройства делятся на унитарные и федеративные.
Основанием деления могут быть различные признаки делимого понятия. Выбор признака зависит от цели деления, от практических задач. Вместе с тем к основанию деления должны предъявляться некоторые требования, важнейшее из которых – объективность основания.
Правила деления
В процессе деления понятия необходимо соблюдать четыре правила, которые обеспечивают четкость и полноту деления.
1. Деление должно быть соразмерным.
Задача деления заключается в том, чтобы перечислить все виды делимого понятия. Поэтому объем членов деления должен быть равен в своей сумме объему делимого понятия.
Правило соразмерности будет нарушено и в том случае, если будут указаны лишние члены деления, то есть понятия, не являющиеся видами данного рода.
2. Деление должно производиться только по одному основанию.
В процессе деления избранный нами признак должен оставаться одним и тем же и не подменяться другим признаком.
3. Члены деления должны исключать друг друга.
Это правило вытекает из предыдущего. Если выбрано не одно основание, то члены деления - видовые понятия - будут находиться в отношении частичного совпадения, как в приведенном выше примере.
4. Деление должно быть непрерывным.
В процессе деления родового понятия нужно переходить к ближайшим видам, не пропуская их. Но нельзя переходить от деления на виды одного порядка к делению на виды другого порядка, такое деление лишено последовательности, оно называется скачком в делении.
Дихотомическое деление, или дихотомия, представляет собой деление объема делимого понятия на два противоречащих понятия. Дихотомическое деление не всегда заканчивается установлением двух противоречащих понятий. Иногда отрицательное понятие вновь делится на два понятия, что помогает выделить из большого круга предметов группу предметов, интересующих нас в каком-либо отношении.
По сравнению с делением по видоизменению признака дихотомическое деление имеет ряд преимуществ. В дихотомии не надо перечислять все виды делимого рода: мы выделяем один вид, а затем образуем противоречащее понятие, в которое включаются все другие виды.
Вместе с тем этот вид деления имеет недостатки. Во-первых, объем отрицательного понятия оказывается слишком широким по объему и неопределенным. Во-вторых, строгим и последовательным является, по существу, лишь деление на два первых противоречащих понятия; при дальнейшем делении эта строгость и последовательность нарушаются. Поэтому дихотомическое деление обычно сводится к делению первого понятия.
Поэтому деление всегда соразмерно. Деление производится только по одному основанию - в зависимости от наличия или отсутствия у предметов некоторого признака.
г) Обобщение и ограничение понятий
Обобщить понятие - значит, перейти от понятия с меньшим объемом, но с большим содержанием к понятию с большим объемом, но с меньшим содержанием.
Обобщение понятия не может быть беспредельным. Наиболее общими являются понятия с предельно широким объемом – категории, например «материя», «сознание, «отношение» и тому подобное. Категории не имеют родового понятия, обобщить их нельзя.
Ограничение понятия представляет собой операцию, противоположенную операции обобщения.
Ограничить понятие -значит, перейти от понятия с большим объемом, но с меньшим содержанием к понятию с меньшим объемом, но большим содержанием.
Пределом ограничения понятия является единичное понятие. Таким образом, изменяя объем исходного понятия, мы изменяем и его содержание, осуществляя тем самым переход к новому понятию – с большим объемом и меньшим содержанием (обобщение) или меньшим объемом и большим содержанием (ограничение).
Логические операции обобщения и ограничения понятий широко применяются в практике мышления: переходя от понятий одного объема к понятиям другого объема, мы уточняем предмет нашей мысли, делаем наше мышление более определенным и последовательным.
Обобщение и ограничение понятий не следует смешивать с мысленным переходом от части к целому и выделением части из целого. Например, сутки делятся на часы, часы на минуты, минуты на секунды. Каждое последующее понятие не является видом предыдущего, которое в свою очередь нельзя рассматривать как родовое. Поэтому переход от понятия «час» к понятию «сутки» – не обобщение, а переход от части к целому; переход от понятия «час» к понятию «минута» – не ограничение, а выделение части из целого.
3. Суждение как форма мысли
а) Виды и структура суждений
Виды простых суждений, которые классифицируются по следующим основаниям.
1. По объему субъекта (по количеству).
Единичные - суждения, включающие утверждение или отрицание об одном предмете. Формула такого суждения:
Частные суждения, в которых что-либо утверждается или отрицается о части предметов некоторого класса. Эта часть может быть неопределенной и определенной. В зависимости от данного обстоятельства частные суждения подразделяются на неопределенные и определенные.
Внеопределенных суждениях логическая схема такова: «Некоторые 8 есть Р». Слово «некоторые» придает им неопределенность.
Определенное частное суждение содержит знание и о той, и о другой части субъекта суждения. Оно имеет такую логическую схему:
Общие - суждения, в которых что-либо утверждается или отрицается в каждом предмете данного класса. Логическая схема таких суждений имеет вид:
«Все S есть Р» или «Ни одно S не есть Р»
2. По качеству связки суждения могут быть утвердительные или отрицательные.
Следует различать отрицательное суждение и негативную форму выражения утвердительного суждения. Такого вида суждения не всегда идентичны.
3. По содержанию предиката суждения делятся на суждения свойства (атрибутивные), суждения отношения (релятивные) и суждения существования (экзистенциальные).
Суждения свойства отражают принадлежность или непринадлежность предмету мысли того или иного свойства, состояния.
Суждения отношения выражают различные связи между предметами мысли по месту, времени, величине и прочее.
Суждения существования призваны решать вопрос о наличии предмета нашей мысли - любого явления природы, общества или духовной жизни.
б) Классификация простых атрибутивных суждений по количеству
и качеству
По качеству и количеству различают четыре вида простых атрибутивных высказываний:
A – от лат. Affirmo – Общеутвердительные («Все люди смертны»)
Общеутвердительное суждение - общее по объему и утвердительное по качеству связки. Его структура: «Все S есть Р»,а символом служит латинская буква «А».
I – от лат. Affirmo – Частноутвердительные («Некоторые люди – студенты»)
Частноутвердительное суждение - частное по объему субъекта и утвердительное по качеству связки. Его структура: «Некоторые S есть Р». Символом частноутвердительных суждений служит буква «I».
E – от лат. Nego – Общеотрицательные («Ни один кит не рыба»)
Общеотрицательное суждение - общее по объему субъекта и отрицательное по качеству связки. Его структура: «Ни одно S не есть Р». Символом общеотрицательных суждений служит буква «Е».
O – от лат. Nego – Частноотрицательные («Некоторые люди не являются студентами»)
Частноотрицательное суждение - частное по объему и отрицательное по качеству связки. Его структура: «Некоторые S не есть Р», а символом служит буква «О».
Единичные высказывания (такие, в которых субъект является единичным термином) приравниваются к общим.
в) Распределенность терминов в простом атрибутивном суждении
Субъект всегда распределен в общем высказывании и никогда не распределен в частном высказывании.
Предикат всегда распределен в отрицательном высказывании и никогда не распределен в утвердительном высказывании.
В качестве предиката, в некоторых случаях, может выступать субъект
В логических операциях с суждениями возникает необходимость установить, распределены или не распределены его термины – субъект и предикат.Термин считается распределенным, если он взят в полном объеме. Термин считается нераспределенным, если он взят в части объема.
Рассмотрим, как распределены термины в суждениях А, Е,I, О.
Суждение А (Все S суть Р). «Все студенты нашей группы (S) сдали экзамены (Р)». Субъект распределен, он взят в полном объеме: речь идет обо всех студентах нашей группы. Предикат этого суждения не распределен, так как в нем мыслится только часть лиц, сдавших экзамены, совпадающая со студентами нашей группы.
Таким образом, в общеутвердительных суждениях S распределен, а Р не распределен. Однако в общеутвердительных суждениях, субъект и предикат которых имеют одинаковый объем, распределен не только субъект, но и предикат. К таким суждениям относятся общевыделяющие суждения, а также определения, подчиняющиеся правилу соразмерности.
Суждение Е (Ни одно S не есть Р). «Ни один студент нашей группы (S) не является неуспевающим (Р)». И субъект, и предикат взяты в полном объеме. Объем одного термина полностью исключается из объема другого: ни один студент нашей группы не входит в число неуспевающих, и ни один неуспевающий не является студентом нашей группы. Следовательно, в общеотрицательных суждениях и S, и Р распределены.
Суждение I (Некоторые S суть Р). «Некоторые студенты нашей группы (S) – отличники (Р)». Субъект этого суждения не распределен, так как в нем мыслится только часть студентов нашей группы, объем субъекта лишь частично включается в объем предиката. Но и объем предиката лишь частично включается в объем субъекта: не все, а только некоторые отличники – студенты нашей группы.
Следовательно, в частноутвердительном суждении ни S, ни Р не распределены.
Суждение О (некоторые Sне суть Р). «Некоторые студенты нашей группы (S) – не отличники (Р)». Субъект этого суждения не распределен, предикат распределен, в нем мыслятся все отличники, ни один из которых не включается в ту часть студентов нашей группы, которая мыслится в субъекте. Следовательно, в частноотрицательном суждении S не распределен, а Р распределен.
г) Правила вывода из суждений по логическому квадрату
Несравнимыми среди простых являются суждения, имеющие различные субъекты или предикаты. Таковы, например, два суждения: «Среди космонавтов есть летчики»; «Среди космонавтов есть женщины».
Сравнимыми являются суждения с одинаковыми субъектами и предикатами и различающиеся связкой или квантором. Обычно их называют суждениями одинаковой материи. Например: «Все американские индейцы живут в резервациях»; «Некоторые американские индейцы не живут в резервациях».
Отношения между простыми суждениями обычно рассматриваются с помощью мнемонической схемы, называемойлогическим квадратом. Его вершины символизируют простые категорические суждения – А, Е, I, О; стороны и диагонали – отношения между суждениями.
Противоположность (контрарность)
| Противоречие (контрадикторность) |
Среди сравнимых различаютсовместимые и несовместимыесуждения.
К совместимым относятся суждения, которые одновременно могут быть истинными. Различают три вида совместимости: 1)эквивалентность (полная совместимость), 2)частичная совместимость (субконтрарность) и 3)подчинение.
1. Эквивалентными являются такие суждения, которые имеют одинаковые логические характеристики: одинаковые субъекты и предикаты, однотипную – утвердительную или отрицательную – связку, одну и ту же выраженную квантором количественную характеристику. С помощью логического квадрата отношения между простыми эквивалентными суждениями не иллюстрируются.
2. Частичная совместимость характерна для суждений I u О, которые могут быть одновременно истинными, но не могут быть одновременно ложными.
3. Подчинение имеет место междусуждениями А и I, Е и О. Для них характерны следующие две зависимости.
При истинности общего суждения частное всегда будет истинным
При ложности частного суждения общее суждение также будет ложным
Отношение несовместимости.
Несовместимыми являются суждения А и Е, А и О, Е и I, которые одновременно не могут быть истинными. Различают два вида несовместимости: противоположность и противоречие.
1. Противоположными (контрарными) являются суждения А и Е, которые одновременно не могут быть истинными, но могут быть одновременно ложными.
2. Противоречащими (контрадикторными) являются суждения А и О, Е и I, которые одновременно не могут быть ни истинными, ни ложными.
Hесовместимые единичные суждения могут находиться лишь в отношении противоречия и не могут находиться в отношении противоположности, ибо каждому отдельному предмету может быть либо присущ, либо не присущ определенный признак.
4. Умозаключение как форма мысли
а) Понятие и виды умозаключений
Умозаключение - это форма мышления, позволяющая из одного или нескольких суждений, называемых посылками, извлекать с помощью правил логики новое суждение - заключение.
В умозаключении различают посылки - высказывания, представляющие исходное знание, и заключение - высказывание, к которому мы приходим в результате умозаключения. В естественном языке существуют слова и словосочетания, указывающие как на заключение («значит», «следовательно», «отсюда видно», «поэтому», «из этого можно сделать вывод» и тому подобное), так и на посылки умозаключения («так как», «поскольку», «ибо», «принимая во внимание, что...», «ведь» и тому подобное). Представляя суждение в некоторой стандартной форме, в логике принято указывать вначале посылки, а потом заключение, хотя в естественном языке их порядок может быть произвольным: вначале заключение - потом посылки; заключение может находиться «между посылками». В приведенном в начале главы примере посылками служат два первых высказывания, а заключением - третье высказывание («плотность Земли не одинакова во всех ее частях»),
Понятие умозаключения как логической операции тесно связано с понятием логического следования. Учитывая эту связь, мы различаем правильные и неправильные умозаключения. Умозаключение, представляющее собой переход от посылок к заключению, является правильным, если между посылками и заключением имеется отношение логического следования. В противном случае - если между посылками и заключением нет такого отношения - умозаключение неправильно. Естественно, что логику интересуют лишь правильные умозаключения. Что же касается неправильных, то они привлекают внимание логики лишь с точки зрения выявления возможных ошибок. В делении умозаключений на правильные и неправильные мы должны различать отношение логического следования двух видов дедуктивное и индуктивное. Первое гарантирует истинность заключения при истинности посылок. Второе - при истинности посылок - обеспечивает лишь некоторую степень правдоподобия заключения (некоторую вероятность его истинности). Соответственно этому умозаключения делятся на дедуктивные и индуктивные. Первые иначе еще называют демонстративными (достоверными), а вторые – правдоподобными (проблематичными).
б) Простой категорический силлогизм: правила, фигуры и модус
В силлогизм входит ровно три термина:
· S – меньший термин: субъект заключения (входит также в меньшую посылку);
· P – больший термин: предикат заключения (входит также в большую посылку);
· M – средний термин: входит в обе посылки, но не входит в заключение
Подлежащие S (субъект) – то, относительно чего мы высказываем (делится на два вида):
1. Определенное: Единичное, Частное, Множественное
· Единичные (суждения) – в которых подлежащее является индивидуальным понятием. Прим: «Ньютон открыл закон тяготения»
· Частное суждение – в котором подлежащим суждения является понятие, взятое в части своего объема. Прим: «Некоторые S суть P»
· Множественное суждение - это те, в которых несколько подлежащих классовых понятий. Прим: «насекомые, пауки, раки есть членистоногие»
2. Неопределенное. Прим: «светает», «больно» и тому подобное.
Сказуемое P (предикат) – то, что мы высказываем (3 вида суждений):
· Повествовательные – это суждение относительно событий, состояний, процессов или деятельности скоропроходящих. Прим: «Роза в саду цветет».
· Описательные – когда одному или многим предметам приписывается какое-нибудь свойство. Субъектом всегда является определенная вещь. Пример: «Огонь горяч», «снег бел».
Отношение между подлежащим и сказуемым:
1. Суждения тождества – понятия субъекта и предиката имеют один и тот же объем. Прим: «всякий равносторонний треугольник есть равноугольный треугольник»
2. Суждения подчинения – понятия с менее широким объемом подчиняется понятию с более широким объемом. Прим: «Собака есть домашнее животное»
3. Суждения отношения - именно пространства, времени, отношения. Прим: «Дом находится на улице»
Фигурами силлогизма называются формы силлогизма, отличающиеся расположением среднего термина в посылках:
| Фигура 1 | Фигура 2 | Фигура 3 | Фигура 4 | |||||
| Бо́льшая посылка: | M–P | P–M | M–P | P–M | ||||
| Меньшая посылка: | S–M | S–M | M–S | M–S | ||||
| Заключение: | S–P | S–P | S–P | S–P |
Каждой фигуре отвечают модусы – формы силлогизма, различающиеся количеством и качеством посылок и заключения. Модусы изучались ещё средневековыми школами, и для правильных модусов каждой фигуры были придуманы мнемонические имена:
| Фигура 1 | Фигура 2 | Фигура 3 | Фигура 4 | |||
| Barbara | Cesare | Darapti | Bramantip | |||
| Celarent | Camestres | Disamis | Camenes | |||
| Darii | Festino | Datisi | Dimaris | |||
| Ferio | Baroco | Felapton | Fesapo | |||
| Bocardo | Fresison | |||||
| Ferison |
в) Условное и разделительно – категорическое умозаключение
Чисто условным называется умозаключение, обе посылки которого являются условными суждениями.
Схема чисто условного умозаключения:
(р -» q) ^ (q-> г) р->г
Вывод в чисто условном умозаключении основывается на правиле:следствие следствия есть следствие основания.
Умозаключение, в котором заключение получается из двух условных посылок, относится к простым. Однако заключение может следовать из большего числа посылок, которые образуют цепь условных суждений. Такие умозаключения называются сложными.
Условно-категорическим называется умозаключение, в котором одна из посылок –условное, а другая посылка и заключение – категорические суждения.
Это умозаключение имеет два правильных модуса: 1) утверждающий и 2) отрицающий.
1. В утверждающем модусе посылка, выраженная категорическим суждением, утверждает истинность основания условной посылки, а заключение утверждает истинность следствия;
рассуждение направлено от утверждения истинности основания к утверждению истинности следствия.
2. В отрицающем модусе посылка, выраженная категорическим суждением, отрицает истинность следствия условной посылки, а заключение отрицает истинность основания. Рассуждение направлено от отрицания истинности следствия к отрицанию истинности основания.
Из четырех модусов условно-категорического умозаключения, исчерпывающих все возможные комбинации посылок, достоверные заключения дают два: утверждающий (modus ponens) (1) и отрицающий (modus tollens) (2). Они выражают законы логики и называются правильными модусами условно-категорического умозаключения. Эти модусы подчиняются правилу: утверждение основания ведет к утверждению следствия и отрицание следствия – к отрицанию основания. Два других модуса (3 и 4) достоверных заключений не дают. Они называются неправильными модусами и подчиняются правилу: отрицание основания не ведет с необходимостью к отрицанию следствия и утверждение следствия не ведет с необходимостью к утверждению основания.
г) Условно – категорическое умозаключение: правильные и
неправильные модусы
Формула ((а - Ь) л Ь) -» а (3) не является законом логики. Она означает, что нельзя достоверно умозаключить от утверждения следствия к утверждению основания. Люди иногда неправильно умозаключают так: Если бухта замерзла, то суда не могут входить в бухту. Суда не могут входить в бухту. Бухта замерзла. Заключение будет лишь вероятностным суждением, то есть вероятно, что бухта замерзла, но возможно и то, что дует сильный ветер, или бухта заминирована, или существует другая причина, по которой суда не могут входить в бухту. Вероятностное заключение получится и в таком умозаключении: Если данное тело – графит, то оно электропроводно. Данное тело электропроводно. Вероятно, данное тело – графит. Второй вероятностный модус. Это второй модус, не дающий достоверного заключения. Структура его:
Если а, то Ь. Не-а._____ Вероятно, не-Ь. Схема: а -» Ь ~а Вероятно, Ъ
Формула ((а -» Ь) л a) -» b (4) не является законом логики. Она означает, что нельзя принимать заключение за достоверное, умозаключая от отрицания основания к отрицанию следствия.Некоторые врачи ошибочно рассуждают так: Если человек имеет повышенную температуру, то он болен. Данный человек не имеет повышенной температуры.____ Данный человек не болен.
Учащиеся в школе также допускают логические ошибки при построении умозаключений. Вот пример: Если тело подвергнуть трению, то оно нагреется. Тело не подвергли трению. Тело не нагрелось.
Заключение здесь только вероятностное, но не достоверное, ибо тело могло нагреться по какой-либо другой причине (от солнца, в печи и так далее).
Заметим, что приведение такого рода примеров вполне достаточно для того, чтобы показать, что формы умозаключений, выражаемые формулами (3) и (4), неправильны. Но никакое количество примеров применения форм, соответствующих формулам (1) и (2), не в состоянии – если мы оперируем только примерами – обосновать их логической правильности. Для такого обоснования требуется уже некоторая логическая теория. Такая теория, фактически отсутствующая в традиционной логике, содержится в алгебре логики. Если формула, в которой конъюнкция посылок и предполагаемое заключение соединены знаком имп
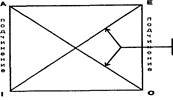 Частичная совместимость (субконтрарность)
Частичная совместимость (субконтрарность)