Золотая пропорция – критерий гармонии и красоты

Существует неразрывная связь между математикой и искусством. Для математики также как и для искусства характерны красота и гармония. В этом можно убедиться при изучении такого математического понятия как «золотая пропорция».

С древних времен люди в своих творениях предпочитают правильные геометрические формы – квадрат, круг, пирамиду и т.д. Симметричные фигуры предпочтительнее, чем несимметричные.

При создании произведений искусства пользовались различными пропорциями. Но из многих пропорций, которыми издавна пользовался человек, существует одна, единственная и неповторимая, обладающая уникальными свойствами. Она отвечает такому делению целого на две части, при котором отношение большей части к меньшей равно отношению целого к большей части. Эту пропорцию называли по разному: «золотой», «божественной», «золотым сечением», «золотым числом».

Если симметричность в архитектуре придает зданиям величественность, совершенность, но она «холодная», «неподвижная», то золотая пропорция придает зданиям грацию, неповторимую индивидуальность, особую гармонию – «подвижную» и «одухотворенную».

Если определении золотой пропорции перевести на язык формул, то получим:

, т.к. x > 0, то

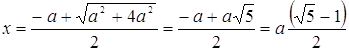
Принято обозначать: 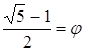. Число носит название коэффициента золотого сечения; =0,61803389… или =0,618. Заметим, что:

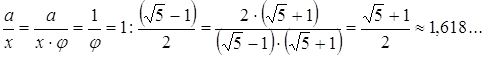
Принято обозначать:

.

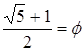Актуальность выбора темы обусловлена необходимостью эстетического развития, а также необходимостью показать неразрывную связь математики и искусства.

Практическая ценность – данный материал может быть использован студентами, школьниками, педагогами.

1. об истоке золотой пропорции

Древнейшие сведения о золотой пропорции относятся ко времени расцвета античной культуры. О ней упоминается в трудах великих философов Греции: Пифагора, Платона, Евклида. Сведения о геометрическом делении отрезка в крайнем и среднем отношении встречаются во второй книге «Начал» Евклида (III в. до н.э.). После Евклида исследованием золотой пропорции занимались Гипсикл (II в. до н.э.), Папп Александровский (III в. до н.э.) и другие исследователи.

Платон привел формулировку золотого сечения, одну из самых древних, дошедшую до нашего времени. Сущность ее сводится к тому, что для соединения двух частей с третьей совершенным образом необходима пропорция, которая бы «скрепила» их в единое целое. При этом одна часть целого должна так относиться к другой, как целое к большей части.

В эпоху итальянского Возрождения золотая пропорция возводится в ранг главного эстетического принципа. Леонардо да Винчи именует ее «Sectio autea», откуда и получил начало термин «золотое сечение». По мнению белорусского ученого Э.Сороко, термин «золотое сечение» идет от Клавдия Птоломея, который дал это название числу 0,618. Лука Пачоли в 1509г. Пишет первое сочинение о золотой пропорции, названной им «Божественной». Иоганн Кеплер говорит о ней как о «бесценном сокровище», как об одном из двух сокровищ геометрии.

После И.Кеплера золотое сечение было предано забвению, и около 200 лет о нем никто не вспоминал. Лишь в 1850 году немецкий ученый Цейзинг открыл его снова.

Сейчас невозможно достоверно установить ни человека, впервые открывшего золотую пропорцию, ни время, когда это произошло. Очевидно, ее неоднократно открывали, забывали и открывали заново в разное время и в различных странах. Многие исследователи считают первооткрывателем золотой пропорции греческого математика и философа Пифагора.

Он родился в 570г. до н.э. на острове Самосее. В Кротоне основал «Пифагорейский союз». Музыка, гармония и числа – эти три понятия неразрывно связаны друг с другом в учении пифагорейцев. Математика являлась одной из основ их религии. Они сделали много открытий, написали труды по математике, музыке, философии, но эти труды не сохранились, о них можно судить лишь на основании более поздних публикаций ученых древности.

Ямвлих во «Введении в Никомахову арифметику» говорит, что Пифагор нашел золотую пропорцию и что этому … он научился у вавилонян.

Эстафета знаний древности ведет от Греции к Египту, а от него к Вавилону. Но ведь и знания народов Двуречья не возникли на пустом месте, их корни также уходят в другие эпохи и другие страны. В поисках истоков золотой пропорции следует прежде всего направиться в Древний Египет, к его загадочным пирамидам – хранилищам многих неразгаданных тайн. Их создание свидетельствует о значительном уровне знаний в области геометрии, которыми владели зодчие.

Невозможно с полной уверенностью утверждать, что египетские зодчие имели научное представление о золотой пропорции и ее математических свойствах. Но бесспорно, что они знали и сознательно применяли замечательные треугольники: священный со сторонами 3:4:5, треугольник со сторонами 1:2:, гармонический треугольник с отношением сторон 1: и 1:, а в них содержится золотая пропорция и «около нее нельзя было пройти мимо». (7)

Чем больше изучаешь древние культуры, тем больше убеждаешься в наличии глубоких корней, в преемственности многих знаний. Ведь и египетская наука не возникла на пустом месте. Она наследовала знания других народов, других эпох, и прежде всего Двуречья. Существует гипотеза, что некоторые свои знания египтяне получили от жителей Атлантиды. Возможно, что истоки открытия золотой пропорции кроются в Двуречье, Атлантиде.

Однако, следы золотой пропорции удалось обнаружить 20-25 тыс. лет назад, при археологических раскопках на реке Ангаре в Сибири. М.Герасимов обнаружил прямоугольную пластинку, изготовленную из бивня мамонта. Пластинка декорирована сложным рисунком спиральной формы, в центре ее отверстие. Размеры пластинки 13,6 8,2 см, что с точностью до 1мм отвечает золотой пропорции.

Около 15 тыс. лет назад в пещерах Франции также обнаружены подобные пропорции. Макс Рафаэль в 1946г. Писал, что изображения бизонов, мамонтов и лошади в этих пещерах находятся в размерах золотой пропорции.

А.Окладников нашел на скалах возле села Шишкино на реке Лене палеолитические рисунки диких коней и козла, размеры которых таковы, что они находятся в соответствии с пропорцией золотого сечения.

Нет необходимости доказывать, что у людей палеолита не было научного представления о золотой пропорции. Применение ими золотой пропорции было итогом творческой интуиции, интуитивного познания мира, итогом стремления к гармонии и красоте.

2. Применение золотой пропорции в различных видах искусства

Искусству присуще стремление к стройности, соразмерности, гармонии. От проявляются в пропорциях архитектуры и скульптуры, в расположении предметов и фигур, сочетании красок в живописи, в чередовании рифм и мерности ритма в поэзии, в последовательности музыкальных звуков. Одна из пропорций, которая чаще всего встречается в искусстве - «золотое сечение».

Многие художники, поэты, скульпторы истинные ценители прекрасного, восхищались красотой человеческого тела.

Эталонами красоты человеческого тела, образцами гармонического телосложения издавна и по праву считаются великие творения греческих скульпторов: Фидия, Поликтета, Мирона, Праксителя. В создании своих творений греческие мастера использовали принцип золотой пропорции. Центр золотой пропорции строения человеческого тела располагается точно в месте пупка. И не случайно величину золотой пропорции принято обозначать буквой ; это сделано в честь Фидия – творца бессмертных скульптурных произведений.

Одним из высших достижений классического греческого искусства может служить статуя «Дорифор» (рис.1) («Копьеносец»), изваянная Поликтетом (рис.1).

Фигура юноши выражает единство прекрасного и доблестного, лежащих в основе греческих принципов искусства. Статуя полна спокойной уверенности; гармония линий, уравновешенность частей олицетворяют могущество физической силы. Широкие плечи почти равны высоте туловища, половина высоты тела приходится на лонное сращение, высота головы 8 раз укладывается в высоте тела, а золотой пропорции отвечает положение пупка на теле атлета.

Шедевром красоты считается Афродита Милосская (III-II вв. до н.э.), созданная Александром. Статуя богини любви и красоты, изваянная Праксителем для храма на острове Книд, считалась его современниками величайшим чудом, превосходящие все другие художественные произведения мира.

В таких работах Фидия, как Зевс Олимпийский, Афина Парфенос, Аполлон Бельведерский, золотое сечение заложено в различных пропорциях человеческого тела. Не только вся статуя, но и отдельные её части делятся в золотом отношении. (3)

В особый вид изобразительного искусства Древней Греции следует выделить изготовление и роспись всевозможных сосудов. В изящной форме амфор и кратеров, а также в их росписи легко угадываются пропорции золотого сечения. (4)

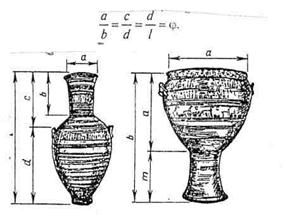
Например, для амфоры (рис 2а) выполняются отношения a/b=c/d=d/e= Амфора на (рис.2б) выдержана в следующих пропорциях: а/b=m/а=. Свои знания в искусстве греки переняли и развили из египетского искусства. Достижения египтян удивляли и восхищали художников Древней Греции.

Они специально совершали путешествия в Египет, чтобы поучиться умению пользоваться каноном.

В живописи, скульптуре храмов, на предметах домашнего обихода древние египтяне чаще всего изображали богов и фараонов. Для этого они установили специальные каноны изображения стоящего человека, идущего, сидячего, колено­преклонённого и т.д. На основе золотого сечения созданы пропорции древнеегипетского канона - восемь пропорциональных величин, который также использовался для создания канонических статуй и рельефов.

В эпоху средневековья достижения античного искусства были преданы забвению. Безвозвратно погибли драгоценные рукописи, в которых содержались теория и математические выкладки по композиции и рисунку величин мастеров.

Рисунок стал условным и схематическим. Нарушены все пропорции человеческой фигуры. (рис.З.)

Наглядно убеждения, что, потеряв знания о математических соразмерностях фигур, художники потеряли и изобразительную силу искусства. Чтобы возродить былые реалистические традиции, нужно было начинать всё сначала. Это выпало на долю художников эпохи Возрождения.

Леонардо да Винчи предпринял ряд измерений, из которых он вычислил средние размеры человека, рассчитал пропорции тела человека и опять приходит к «золотому сечению».

Золотая пропорция занимает ведущее место в художественных канонах Леонардо да Винчи и Дюрера. В соответствии с этими канонами золотая пропорция отвечает не только делению тела на 2 неравные части линией талии, но и высота лица относится к вертикальному расстоянию между дугами бровей и нижней частью подбородка, как расстояние между нижней частью носа и нижней частью подбородка относится к расстоянию между углами губ и нижней частью подбородка; в строении костей пальцев человека, в соотношении чисел различных органов.

При возведении памятников наиболее распространено отношение на основе золотого сечения. Общая высота памятника обычно относится к высоте фигуры, как высота фигуры к постаменту.

Даже в музыке огромное значение имеют пропорции, соотношение частей между собой и отношение каждой части к целому, т.е. и в музыке присутствует золотая пропорция. Если «измерять» музыкальное произведение по времени его исполнения, то точка золотого сечения служит ориентиром формообразования, часто на нее приходится кульминация. Это может быть также самый яркий или самый тихий момент, самое плотное по фактуре место или самое звуковысотное. Но случается и так, что в точке золотого сечения появляется новая музыкальная тема.

По наблюдениям Л.Сабанеева, в музыкальных произведениях различных композиторов обычно констатируется не одно золотое сечение, а целая серия подобных сечений. Каждое такое сечение отражает свое музыкальное событие, качественный скачок в развитии музыкальной темы. В изученных им 1770 сочинениях 42 композиторов наблюдалось 3275 золотых сечений, в 1338 сочинениях наблюдалось хотя бы 1 золотое сечение. Наибольшее количество музыкальных произведений, в которых имеется золотое сечение у Аренского(95%), Бетховена(97%), Гайдна(97%), Моцарта(91%), Скрябина(90%), Шопена(92%), Шуберта(91%).

Проводя аналогию между математикой и литературой, опираясь на данные ученых, можно придти к следующему выводу: в строении стихотворений должна проявляться закономерность музыкальной гармонии, а следовательно, и золотая пропорция.

В коротких стихотворениях размером 4-8 строк, как правило, выражается 1 мысль, 1 эмоциональное состояние поэта. Но стихотворения большие, 12-14 строк или 20-22 строки, очень часто включают в себя 2 мысли, 2 эмоциональных состояния. Поэтому такие стихотворения состоят как бы из 2-х частей, часто эти части не равны по размеру, ассиметричны, отношение большей части к меньшей очень часто близко к золотой пропорции.

Так, например, некоторые стихотворения А.С.Пушкина очень четко отвечают этой закономерности внутренней композиции. К таким стихотворениям относятся: притча «Сапожник» состоящая из 2-х частей 8 и 5 строк; стихотворение «Он между нами жил» - 2 части 13 и 8 строк. Роман «Евгений Онегин» - произведение высочайшего художественного уровня, а 8-я глава – драгоценная жемчужина. Эта глава наиболее совершенна, наиболее отточена, насыщена эмоциональная структура главы, многоплановая, с подъемами и спадами. Письмо Татьяны делит главу на 2 части 32 и 19 стихов, их отношение близко к золотой пропорции.

Рассматривая композицию «Пиковой дамы» приходишь к выводу, что кульминационный момент – приходится на 535 строку из 853 строк. Эта строка расположена почти точно в месте золотого сечения 853:535=1,6.

Наличие золотой пропорции определяет основной план композиции «Пиковой дамы», придает ей ассиметричность – медленное нарастание эмоционального напряжения, кульминация и постепенный спад накала. Повесть состоит из 6 глав, и каждая узловатая точка глав отвечает точке золотого сечения:

1 глава – 110 строк – узловатая точка 68 строка;

2 глава – 219 строк – кульминационный момент 135 строка;

3 глава – 212 строк – золотое сечение соответствует 131 строке;

4 глава – 113 строк – золотая пропорция приходится на 70 строку;

5 глава – 75 строк – 46-я строка соответствует золотому сечению.

Золотая пропорция присутствует и в композиции других произведений А.С.Пушкина: «Станционный смотритель», «Метель», «Гробовщик».

Совпадение кульминационных моментов в произведениях прозы у А.С.Пушкина с золотой пропорцией удивительно близкое, в пределах 1-3 строк. Чувство гармонии у него было развито необыкновенно, что объективно подтверждает гениальность великого поэта и писателя.

Аналогично, золотую пропорцию можно обнаружить и в некоторых произведениях В.Брюсова, например «Сонет к форме».

Многие исследователи находили проявления золотой пропорции в произведениях великих художников. Речь идет не только о пропорциях обнаженного тела, а о композиционных основах произведений живописи. Наличие золотой пропорции в композиции произведений художников придавало им гармоническую законченность, совершенство и одновременно подвижность, динамизм, оживляло композицию. (10)

Характерным примером такого рода могут служить картины известного японского художника Хокусая: «Фудзи и путник», «Мост Парчового пояса», «Фудзи в гору», «Перевал Инуме в провинции Кай»; картина Сурикова «Барыня Морозова» и другие.

Изучая явления и объекты живой и неживой природы исследователи пришли к выводу, что и здесь проявляется золотая пропорция.

Например, ее можно обнаружить в строении листа клена, в отношениях длин хвоста и корпуса стрекозы, в строении цветка розоцветных и другое.

Закономерности золотой пропорции широко распространены в природе, проявляются на самых различных уровнях – от атомных сочетаний до строения тел высших животных.

Проявление золотой пропорции в различных видах искусства дает основание предполагать наличие единых критериев гармонии, общих как для творений природы, так и для произведений, созданных художниками, композиторами, поэтами, скульпторами. Это единство роднит произведения искусства и творения природы, определяет их преемственность, сущность прекрасного.

3.ЗАКОНОМЕРНОСТИ ЗОЛОТОЙ ПРОПОРЦИИ В АРХИТЕКТУРЕ

«Божественную пропорцию» использовали при возведении величественных греческих храмов, пирамид.

Одно из семи чудес света - египетские пирамиды. Эти фигуры поражают своими размерами, совершенством геометрических фигур.

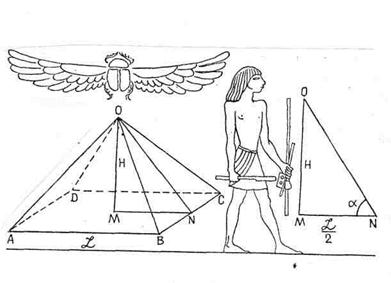Исследователи довольно подробно изучали пирамиду Хеопса - угол наклона граней пирамиды равен 51⁰51^/, tg 51⁰51^/ = 1,27306 или отвечает отклонению высот пирамиды к половине ее основания, что очень близко к корню квадратному золотой пропорции = 1,27202. Высота пирамиды ОН - 318 локтей, сторона основания АВ - 500 локтей, апофема боковой грани ON = 404,5 локтя (рисунок 4).

MN=AB;

Как видно, отклонение длины апофемы боковой