Люминесцентные свойства нанокристаллов сульфида кадмия

В настоящее время наблюдается интенсивное развитие физики полупроводников, размеры которых порядка нанометров. Полупроводниковые наноразмерные частицы находятся в области перехода между молекулярной структурой и твердым телом. Оптические, электронные и каталитические свойства полупроводникового нанокристалла существенно отличаются от таковых для макрокристаллического вещества и зависят от размера частицы (эффект размерного квантования). Такие полупроводники дают возможность управлять их оптическими, электрическими и структурными свойствами, изменяя размеры частиц. Особенно сильное изменение оптических свойств наблюдается в случае, когда размер нанокристалла меньше, чем диаметр основного экситона.

С тех пор, как эффект размерного квантования был впервые обнаружен, научные исследования этого явления стремительно развиваются. Некоторые группы ученых уже показали возможные сферы применения таких материалов: солнечные элементы, светодиоды, точечные транзисторы, светофильтры, полосу поглощения которых можно изменять только изменением размеров частиц. А также как новый класс - нелинейные оптические материалы.

В случае точечных транзисторов, применение основано на дискретности электронных уровней полупроводника в сильно-квантованном режиме.

На сегодняшний день качество образцов значительно улучшается, теперь существует возможность приготовить нанокристалл любого диаметра в пределах от 2-5 до 50 нм с ошибкой не менее 5%.

В связи с таким бурным развитием данного направления физики полупроводников возникает необходимость изучения свойств полупроводниковых нанокристаллов. Особо актуальным является вопрос о стабильности оптических и люминесцентных характеристик нанокристаллов в процессе их хранения.

В связи с вышеизложенным целью моей работы являлось изучение люминесцентных свойств нанокристаллов сульфида кадмия и исследование зависимости полос люминесценции от воздействия внешних факторов.

1.ЛЮМИНЕСЦЕНТНЫЕ СВОЙСТВА СУЛЬФИДА КАДМИЯ

1.1. Эффект размерного квантования в полупроводниках

В последние годы появились эксперименты (1-3, 4-9), в которых исследуются оптические свойства систем, представляющих диэлектрическую матрицу с вкрапленными в нее частицами полупроводника. Технология этих систем такова, что полупроводниковые частички с достаточно хорошей точностью можно считать шарообразными, причем дисперсия их радиусов сравнительно невелика. Очень важно, что технология позволяет получать системы, в которых средний радиус полупроводниковых частиц меняется практически непрерывно. Поэтому исследования оптических свойств этих систем в зависимости от радиуса шаров представляет мощный метод изучения параметров полупроводников, в значительной мере аналогичный магнитооптическому.

В полупроводниковом шаре возникает размерное квантование электронных и дырочных состояний, приводящих к тому, что оптические линии смещаются в зависимости от радиуса шара (1-3). Авторы предлагают здесь теоретическое описание этого явления в рамках простейшей модели, использующей стандартную зонную схему.

Предполагалось, что зоны электронов и дырок имеют параболическую форму с массами m_e и m_h соответственно, причем m_e<h. Тогда характер размерного квантования определяется соотношением трех длин: a, a_e, a_h, где a_e>a_h; а – радиус шара, a_e, a_h– боровские радиусы электронов и дырок, соответственно, в полупроводнике с диэлектрической проницаемостью e. Предполагаемая теория построена в приближении метода эффективной массы, т.е. в предположении, что существенные длины велики по сравнению с постоянной решетки. Волновая функция электронов и дырок будет считаться равной нулю на поверхности шара, что соответствует бесконечно высокой потенциальной стенке.

Рассмотрим случай сильного размерного квантования, когда a>>a_h. Расстояние между уровнями размерного квантования для электронов и дырок порядка ħ²/(m_e·a²) и ħ²/(m_h·a²).

При межзонном поглощении должна наблюдаться серия дискретных линий. Порогом поглощения является величина

(1.1),

где - ширина запрещенной зоны; - приведенная масса.

Учет дисперсии шаров по размерам приводит к замене выражения для порога поглощения (1.1) на следующее:

(1.2).

Отсюда виден закон, по которому эффективная ширина запрещенной зоны увеличивается с уменьшение радиуса шара а, прочие линии сдвигаются в коротковолновую сторону по закону

(1.3),

где - корни функции Бесселя.

Если ширина линий сравнима с расстоянием между ними, то размерное квантование должно проявляться апериодическими осцилляциями поглощения, причем максимумы осцилляций должны сдвигаться в коротковолновую сторону по закону 1/а².

1.2. Методы получения и оптические свойства наночастиц сульфида кадмия

Как было недавно обнаружено (6), трехмерные микрокристаллы полупроводниковых соединений могут быть выращены в объеме прозрачной диэлектрической матрицы силикатного стекла, и их образование может быть непосредственно детектировано по спектрам оптического поглощения. При этом оказалось, что средний размер микрокристаллов в матрице можно направленно менять в процессе выращивания в широких пределах от десятков до нескольких сотен ангстрем.

Синтез полупроводниковых соединений в диэлектрической матрице, кроме принципиально важной возможности получения кристаллов микроскопических размеров, имеет еще одно преимущество. Действительно, поскольку концентрации кристаллической фазы в матрице относительно невелика, оказывается возможной непосредственно записывать спектры поглощения кристаллов на относительно толстых образцах, получаемых механической полировкой (3). Таким образом, подобные гетерогенные стекла оказываются новым, чрезвычайно удобным объектом для исследования размерных эффектов в полупроводниках.

В работе (6) рассматривается выращивание микрокристаллов в многокомпонентном силикатном стекле, в котором полупроводниковая фаза, концентрации приблизительно 1%, была растворена в течение синтеза. При вторичной термической обработке стеклянных образцов зародышеобразование и рост полупроводниковых микрокристаллов происходит в результате диффузионного фазового разложения пересыщенного твердого раствора.

На рис.1.1 показана экспериментальная зависимость среднего радиуса микрокристалла CdS как функция времени нагрева для ряда температур. Величина среднего радиуса микрокристалла для образца была определена методом малоуглового рентгеновского рассеяния в аппроксимации сферических частиц. Наблюдаемые зависимости описаны выражением, полученным в теоретической статье для диффузного фазового разложения пересыщенного твердого раствора в стадии переконденсации:

(1.4),

где - коэффициент диффузии, α – коэффициент, который определен граничным поверхностным натяжением, и t – время термообработки. Таким образом, выбирая надлежащие условия термической обработки (температура и время), можно варьировать размер микрокристаллов управляемым способом (7). Было также показано, что

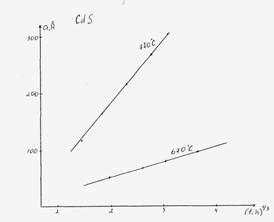
Рис. 1.1. Зависимость среднего радиуса микрокристалла CdS от времени нагрева t при различных температурах термообработки (7).

стадия роста переконденсации характеризуется стационарным (установившимся) состоянием распределения по размерам, которое не зависит от начальных условий, и для этого распределения было получено аналитическое выражение. Это выражение фактически описывает распределение по размерам полупроводниковых частиц, выращенных по рассматриваемой методике (6). Этот факт дает возможность принять во внимание дисперсию размеров микрокристаллов при выполнении количественного анализа экспериментальных результатов, рассмотренную в этом параграфе.

Также наночастицы CdS получали (10, 11) путем быстрого смешивания при комнатной температуре водных растворов сульфата кадмия, содержащих стабилизатор с эквимолярными количествами сульфида натрия в небольшом объеме воды. В качестве стабилизаторов использовали желатин и поливиниловый спирт (ПВС). Величина смещения края полосы поглощения, как показали опыты, зависит от природы стабилизатора, его количества, а так же от содержания образовавшегося сульфида кадмия. У частиц, стабилизированных добавками ПВС, она невелика и составляет лишь 15-20 нм (рис.1.2 а, спектр 1) , тогда как при стабилизации желатином край полосы поглощения может сдвигаться на 60 нм (рис.1.2 а, спектр 3) и даже больше. Использование корреляционной зависимости между пороговой длиной волны поглощения и диаметром кристаллита позволило получить оценочные величина среднего размера частиц, характеризующихся спектрами 1 и 3 (рис.1.2 а). Они имеют значения, близкие к 5 нм и к 3 нм, соответственно. Необходимо отметить при этом, что наличие в спектре (рис.1.2) достаточно хорошо разрешенного экситонного пика при 360 нм может служить указанием на относительно узкое распределение частиц по размерам в растворах, стабилизированных желатином. При большей концентрации CdS этот пик становится менее выраженным, появляется дополнительное поглощение в области 370-450 нм и край полосы, характеризующийся максимумом при 360 нм, поскольку смещается в длинноволновую сторону (рис.1.2 а, спектр 2). Все это свидетельствует о том, что наряду с частицами, которым принадлежит спектр 3, присутствуют также более крупные образования.

Как видно из рис.1.2 б, на спектры поглощения коллоидных растворов CdS существенное влияние оказывает концентрация желатина. В растворах, содержащих 0.5 и 0.25% желатина, образуются наборы малых частиц с узким распределением по размерам (спектры 1 и 2). При переходе к более разбавленным растворам происходят изменения, подобные тем, которые наблюдаются при повышении концентрации CdS (спектры 3 и 4), а при стабилизации 0.01% желатином получаются частицы, которые, судя по краю полосы, расположенному около 500 нм, имеют диаметр, близкий к 5 нм (спектр 5). В противоположность рассмотренному случаю, варьирование концентрации ПВС от 0.1 до 5% практически не влияет на спектры поглощения; они во всех случаях остаются такими же, как спектр 1 на рис. 1.2,а.