Корни многочленов от одной переменной

§1. Многочлены от одной переменной

Понятие многочлена. Степень многочлена

Равенство многочленов. Значение многочленов

Операции над многочленами

Схема Горнера

Корни многочленов

Кратные корни многочлена

Рациональные корни многочлена

§ 2. Задачи о многочленах

Заключение

Список литературы

Введение

Тема моей курсовой работы "Многочлены".

В ней я хочу дать понятие многочлена, определить операции над ними, рассмотреть способы нахождения остатков при делении: схема Горнера. А так же рассмотреть виды корней: рациональные, кратные.

Для этого мне нужно изучить научную и методическую литературу, подобрать и решить задачи по данной теме, включая олимпиадные.

В первой главе своей работы я рассматриваю основное понятие многочлена, операции над ними, ввожу определение и основные понятия схемы Горнера, рассматриваю кратные и рациональные корни многочлена. Во второй главе решаю задачи, включая олимпиадные.

§1. Многочлены от одной переменной

Понятие многочлена. Степень многочлена

Многочленом от переменной х будем называть выражение вида

a_nxⁿ+a_n-1x^n-1+... +a₁x+a_0,где n - натуральное число; а_n,a_n-1,..., a₁, a₀ - любые числа, называемые коэффициентами этого многочлена. Выражения a_nxⁿ, a_n-1x^n-1,..., a₁х, a₀ называются членами многочлена, а₀ - свободным членом.

Часто будем употреблять и такие термины: a_n - коэффициент при хⁿ, а_n-1- коэффициент при х^n-1 и т.д.

Примерами многочленов являются следующие выражения: 0х⁴+2х³+ (-3) х³+ (3/7) х+; 0х²+0х+3; 0х²+0х+0. Здесь для первого многочлена коэффициентами являются числа 0, 2, - 3, 3/7, ; при этом, например, число 2 - коэффициент при х³, а - свободный член.

Многочлен, у которого все коэффициенты равны нулю, называется нулевым.

Так, например, многочлен 0х²+0х+0 - нулевой.

Из записи многочлена видно, что он состоит из нескольких членов. Отсюда и произошел термин ‹‹многочлен›› (много членов). Иногда многочлен называют полиномом. Этот термин происходит от греческих слов πολι - много и νομχ - член.

Многочлен от одной переменной х будем обозначать так: f (x), g (x), h (x) и т.д. например, если первый приведённых выше многочленов обозначить f (x), то можно записать: f (x) =0x⁴+2x³+ (-3) x²+3/7x+.

Для того чтобы запись многочлена выглядела проще и выглядела компактнее, договорились о ряде условностей.

Те члены не нулевого многочлена, у коэффициенты равны нулю, не записывают. Например, вместо f (x) =0x³+3x²+0x+5 пишут: f (x) =3x²+5; вместо g (x) =0x²+0x+3 - g (x) =3. Таким образом, каждое число - это тоже многочлен. Многочлен h (x), у которого все коэффициенты равны нулю, т.е. нулевой многочлен, записывают так: h (x) =0.

Коэффициенты многочлена, не являющиеся свободным членом и равные 1, тоже не записывают. Например, многочлен f (x) =2x³+1x²+7x+1 можно записать так: f (x) =x³+x²+7x+1.

Знак ‹‹-›› отрицательного коэффициента относят к члену, содержащему этот коэффициент, т.е., например, многочлен f (x) =2x³+ (-3) x²+7x+ (-5) записывают в виде f (x) =2x³-3x²+7x-5. При этом, если коэффициент, не являющийся свободным членом, равен - 1, то знак "-" сохраняют перед соответствующим членом, а единицу не пишут. Например, если многочлен имеет вид f (x) =x³+ (-1) x²+3x+ (-1), то его можно записать так: f (x) =x³-x²+3x-1.

Может возникнуть вопрос: зачем, например, уславливаться о замене 1х на х в записи многочлена, если известно, что 1х=х для любого числа х? Дело в том, что последнее равенство имеет место, если х - число. В нашем же случае х - элемент произвольной природы. Более того запись 1х мы пока не имеем права рассматривать как произведение числа 1 и элемента х, ибо, повторяем х - это не число. Именно таким обстоятельством и вызваны условности в записи многочлена. И если мы дальше говорим все-таки о произведении, скажем, 2 и х без всяких оснований, то этим допускаем некоторую нестрогость.

В связи с условностями в записи многочлена обращаем внимание на такую деталь. Если имеется, например, многочлен f (x) =3х³-2х²-х+2, то его коэффициенты - это числа 3, - 2, - 1,2. Конечно, можно было бы сказать, что коэффициентами являются числа 0, 3, - 2, - 1, 2, имея в виду такое представление данного многочлена: f (x) =0x⁴-3x²-2x²-x+2.

В дальнейшем для определенности будем указывать коэффициенты, начиная с отличного от нуля, в порядке их следования в записи многочлена. Так, коэффициентами многочлена f (x) =2x⁵-x являются числа 2, 0, 0, 0, - 1, 0. Дело в том, что хотя, например, член с х²в записи отсутствует, это лишь означает, что его коэффициент равен нулю. Аналогично свободного члена в записи нет, поскольку он равен нулю.

Если имеется многочлен f (x) =a_nxⁿ+a_n-1x^n-1+... +a₁x+a₀ и a_n≠0, то число n называют степенью многочленаf (x) (или говорят: f (x) - -й степени) и пишут ст. f (x) =. В этом случае a_n называется старшим коэффициентом, а a_nxⁿ - старшим членом данного многочлена.

Например, если f (x) =5x⁴-2x+3, то ст. f (x) =4, старший коэффициент - 5, старший член - 5х⁴.

Рассмотрим теперь многочлен f (x) =a, где а - число, отличное от нуля. Чему равна степень этого многочлена? Легко заметить, что коэффициенты многочлена f (x) =a_nxⁿ+a_n-1x^n-1+... +a₁x+a₀ пронумерованы справа налево числами 0, 1, 2, …, -1, и если a_n≠0, то ст. f (x) =. Значит, степень многочлена - это наибольший из номеров его коэффициентов, отличных от нуля (при той нумерации, о которой только что говорилось). Вернемся теперь к многочлену f (x) =a, a≠0, и пронумеруем его коэффициенты справа налево числами 0, 1, 2, … коэффициент а при этом получит номер 0, а так как все остальные коэффициенты - нулевые, то это и есть самый большой из номеров коэффициентов данного многочлена, отличных от нуля. Значит ст. f (x) =0.

Таким образом, многочлены нулевой степени - это числа, отличные от нуля.

Осталось выяснить, как обстоит дело со степенью нулевого многочлена. Как известно, все его коэффициенты равны нулю, и поэтому к нему нельзя применить данное выше определение. Так вот, условились нулевому многочлену не присваивать никакой степени, т.е. что он не имеет степени. Такая условность вызвана некоторым обстоятельством, которые будут рассмотрены несколько позже.

Итак, нулевой многочлен степени не имеет; многочлен f (x) =a, где а - число, отличное от нуля, имеет степень 0; степень же всякого другого многочлена, как легко заметить, равна наибольшему показателю степени переменной х, коэффициент при которой равен нулю.

В заключение напомним еще несколько определений. Многочлен второй степени f (x) =ax2+bx+c называется квадратным трехчленом. Многочлен первой степени вида g (x) =x+c называется линейным двучленом.

Равенство многочленов. Значение многочленов

Два многочлена f (x) и g (x) считаются равными, если равны их коэффициенты при одинаковых степенях переменной х и свободные члены (или, короче, равны их соответствующие коэффициенты). В этом случае пишут: f (x) =g (x).

Например, многочлены f (x) =x³+2x²-3x+1 и g (x) =2x²-3x+1 не равны, ибо у первого из них коэффициент при х³равен 1, а у второго - нулю (согласно принятым условностям мы можем записать: g (x) =0x³+2x²-3x+1. В этом случае пишут: f (x) ≠g (x). Не равны и многочлены h (x) =2x²-3x+5, s (x) =2x²+3x+5, так как у них коэффициенты при х различны. А вот многочлены f₁ (x) =2x⁵+3x³+bx+3 и g₁ (x) =2x⁵+ax³-2x+3 равны тогда и только тогда, когда а=3, а =-2.

Пусть даны многочлен f (x) =a_nxⁿ+a_n-1x^n-1+... +a₁x+a₀ и некоторое число с. Число f (c) =a_ncⁿ+a_n-1c^n-1+... +a₁c+a₀ называется значением многочлена f (x) при х=с.

Таким образом, чтобы найти f (c), в многочлен вместо х нужно подставить с и провести необходимые вычисления. Например, если f (x) =2x³+3x²-x+5, то f (-2) =2 (-2) ³+ (-2) ²- (-2) +5=3.

Рассмотрим многочлен f (x) =a и найдем, например, f (2). Для этого в многочлен вместо х надо подставить число 2 и произвести необходимые вычисления. Однако в нашем случае f (x) =a и переменной х в явном виде нет. Вспомним, что рассматриваемый многочлен можно записать в видеf (x) =0x+a. Теперь все в порядке, можно подставить значение х=2: f (2) =02+a=a. Заметим, что для данного многочлена f (c) =a при любом с. В частности, нулевой многочлен при любом с принимает значение, равное нулю.

Вообще говоря, многочлен при различных значениях переменной х может принимать различные значения. Нас же довольно часто будут интересовать те значения х, при которых многочлен принимает значение 0. Число с называется корнем многочленаf (x), еслиf (c) =0.

Например, если f (x) =x²-3x+2, то числа 1 и 2 являются корнями этого многочлена, ибо f (1) =0 и f (2) =0. А вот многочлен f (x) =5 корней вообще не имеет. В самом деле, при любом значении х он принимает значение 5, а значит, никогда не принимает значение 0. Для нулевого же многочлена, как легко заметить, каждое число является корнем.

Поиск корней многочленов является одной из важнейших задач алгебры. Находить корни линейных двучленов и квадратных трехчленов учат еще в школе. Что касается многочленов более высоких степеней, то для них такая задача является весьма трудной и не всегда разрешимой. В дальнейшем мы неоднократно будем ею заниматься. А сейчас заметим только, что найти корни многочлена f (x) =a_nxⁿ+a_n-1x^n-1+... +a₁x+a₀ и решить уравнение a_nxⁿ+a_n-1x^n-1+... +a₁x+a₀=0 - это эквивалентные задачи. Поэтому, научившись находить корни многочлена, мы научимся решать соответствующие уравнения, и наоборот.

Обратим внимание на различие между двумя утверждениями: "многочлен f (x) равен нулю (или, что то же самое, многочлен f (x) - нулевой)" и "значение многочлена f (x) при х=с равно нулю". Например, многочлен f (x) =x²-1 не равен нулю, ибо у него есть ненулевые коэффициенты, а его значение при х=1 равно нулю. Короче, f (x) ≠0, а f (1) =0.

Между понятиями равенства многочленов и значения многочлена существует тесная взаимосвязь. Если даны два равных многочлена f (x) и g (x), то их соответствующие коэффициенты равны, а значит, f (c) = g (c) для каждого числа с. Другими словами, если f (c) = g (c) для каждого числа c, то равны ли многочлены f (x) и g (x)? Попробуем ответить на этот вопрос в частном случае, когда f (x) = px² +qx+r, а g (x) = kx+m. Так как f (c) = g (c) для каждого числа с, то, в частности, f (0) = g (0),f (1) = g (1),f (-1) = g (-1).

Вычислив фигурирующие в этих равенствах значения рассматриваемых многочленов, получим систему

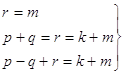
Из этой системы следует, что p = 0, q = k, r = m, а значит, f (x) = g (x).

Таким образом, для рассмотренного примера ответ на поставленный вопрос положителен. Оказывается, это справедливо и в общем случае, после ознакомления с некоторыми другими понятиями и утверждениями теории многочленов.

Операции над многочленами

Многочлены можно складывать, вычитать и умножать по обычным правилам раскрытия скобок и приведения подобных членов. При этом в результате снова получается многочлен. Указанные операции обладают известными свойствами:

f (x) +g (x) =g (x) +f (x),

f (x) + (g (x) +h (x)) = (f (x) +g (x)) +h (x),

f (x) g (x) =g (x) f (x),

f (x) (g (x) h (x)) = (f (x) g (x)) h (x),

f (x) (g (x) +h (x)) =f (x) g (x) +f (x) h (x).

Установим еще несколько полезных свойств операций над многочленами.

Пусть даны два многочлена f (x) =a_nxⁿ+a_n-1x^n-1+... +a₁x+a₀, a_n≠0, и g (x) =b_mx^m+b_m-1x^m-1+... +b₁x+b_m≠0. Ясно, что ст. f (x) =, а ст. g (x) =m. Нетрудно заметить, что если перемножить эти два многочлена, получится многочлен вида f (x) g (x) =a_nb_mx^m+n+... +a₀b₀. Так как a_n≠0 и b_n≠0, то a_nb_m≠0, а значит, ст. (f (x) g (x)) =m+n. Отсюда следует важное утверждение.

Степень произведения двух ненулевых многочленов равна сумме степеней сомножителей, или, короче, ст. (f (x) g (x)) =ст. f (x) +ст. g (x).

Легко доказать, что аналогичное утверждение имеет место для любого конечного числа ненулевых сомножителей, т.е. что ст. (f₁ (x) f₂ (x)... f_s (x)) = ст. f₁ (x) +ст. f₂ (x) +... +ст. f_s (x).

Из рассуждений, приведенных выше для степени произведения двух многочленов, следует два полезных утверждения, которые легко распространяются на любое конечное число сомножителей.

Старший член (коэффициент) произведения двух ненулевых многочленов равен произведению старших членов (коэффициентов) сомножителей.

Свободный член произведения двух многочленов равен произведению свободных членов сомножителей.

Степени многочленов f (x),g (x) и f (x) ±g (x) связаны следующим соотношением: ст. (f (x) ±g (x)) ≤ max ст. f (x), ст. g (x) .

Напомним, что многочлен - выражение вид a_nxⁿ+a_n-1x^n-1+ … + +a₁x+a₀.

Будут ли многочленами выражения: 2x²+4+3x³; (x²-1) (2x+5); (x²+1) (x-3) + 2x?

Попробуем разобраться в этом.

Первое выражение можно рассматривать как сумму многочленов f₁ (x) =2x², f₂ (x) +4, f_a (x) +3x³. Но, как известно, сумма многочленов - это тоже многочлен. Значит, первое выражение можно считать неудачно записанным многочленом. Воспользовавшись тем, что при сложении многочленов слагаемые можно переставлять местами, получим 2x²+4+3x³ = f₁ (x) +f₂ (x) + f₃ (x) =f₃ (x) +f₁ (x) +f₂ (x) =3x³+2x²+4.

Аналогично второе выражение - это произведение многочленов g₁ (x) =x²-1 и g₂ (x) =2x+5, а значит, тоже многочлен. Легко убедиться, что и третье выражение также является многочленом.

Теперь познакомимся с еще одной операцией над многочленами - суперпозицией.

Суперпозицией многочленов f (x) и g (x) называется многочлен, обозначаемый f (g (x)), который получается если в многочлене f (x) вместо x подставить многочлен g (x).

Например, если f (x) =x²+2x-1 и g (x) =2x+3, то f (g (x)) =f (2x + 3) = (2x+ 3) ²+2 (2x+3) - 1=4x²+16x+14,g (f (x)) =g (x²+2x-1) =2 (x²+2x - 1) +3=2x²+4x+1.

Видно, что f (g (x)) ≠g (f (x)), т.е. суперпозиция многочленов f (x), g (x) и суперпозиция многочленов g (x), f (x) различны. Таким образом, операция суперпозиции не обладает свойством переместительности.

Схема Горнера

Разделить с остатком многочлен f (x) на ненулевой многочлен g (x) - это значит представить f (x) в виде f (x) =g (x) s (x) +r (x), где s (x) и r (x) -многочлены и либо r (x) =0, либо ст. r (x) < ст. g (x). S (x) назовем неполным частным, а r (x) - остатком при делении f (x) на g (x).

Неполное частное при делении можно найти с помощью простого правила, называемого схемой Горнера, которое, кстати, позволяет найти и остаток.

Пусть f (x) =a_nxⁿ+a_n-1x^n-1+ … +a₁x+a_0, a_n≠0 - многочлен n-й степени. При делении его на x - c мы получим неполное частное s (x) и остаток r, т.е.f (x) = (x - c) s (x) + r. Так как ст. f (x) = n, а ст. (x - c) = 1, то

ст. s (x) = n - 1, т.е. s (x) = b_n-1x^n-1 + b_n-2x^n-2 + … + b₁x+ b₀, b_n-1 ≠ 0. Таким обрзом, имеем равенство

a_nxⁿ+a_n-1x^n-1+ … +a₁x+a₀ = (x - c) (b_n-1x^n-1+b_n-2x^n-2+ …+b₁x+b₀) +r.

Многочлены, стоящие в левой и правой частях этого соотношения, равны, а значит, равны их соответствующие коэффициенты. Приравняем их, раскрыв предварительно скобки и приведя подобные члены в правой части данного равенства. Получим:

a= b_n-1,a_-1 = b_n-2 - cb_n-1,a_-2 = b_n-3 - cb_n-2,

a₂ = b₁ - cb_2,a₁ = b₀ - cb_1,a₀ = r - cb₀.

Напомним, что требуется найти неполное частное, т.е. его коэффициенты, и остаток.

Выразим их из полученных равенств:

b_n-1 = a_n,

b _n-2 = cb_n-1 + a_n-1,b _n-3 = cb_n-2 + a _n-2,

b₁ = cb₂ + a_2,b₀ = cb₁ +a_1,r = cb₀ + a_0.

Мы нашли формулы, по которым можно вычислять коэффициенты неполного частного s (x) и остаток r. При этом вычисления оформляются в виде следующей таблицы; она называется схемой Горнера.

Таблица 1.

Коэффициенты f (x)