Интегральные схемы с перестраиваемой структурой. Особенности экспериментального и математического моделирования

УО БГУИР

Кафедра ЭВС

РЕФЕРАТ

На тему:

"Интегральные схемы с перестраиваемой структурой. Особенности экспериментального и математического моделирования"

МИНСК, 2008

ИС с перестраиваемой структурой.

Разработка каждой новой ИС сопряжена со значительными затратами. В силу известных трудностей унификации аналоговых и импульсных ИС все же велико. Поэтому в настоящее время разрабатываются схемы с перестраиваемой структурой. Перестройку можно осуществлять двумя методами: с помощью формирования недостающих соединений печатного монтажа ИС и с помощью электрического управления.

Сущность первого метода проиллюстрируем на примере логических монолитных ИС марки ХС-157, выпускаемой фирмой "Моторола".

В кремниевой подложке сформированы 12 одинаковых ДТЛ, принципиальная схема которых приведена на рис. 1.17. ДТЛ-схема выполняет операцию НЕ-ИЛИ. В каждой ДТЛ-схеме отсутствуют соединения диодов с выходными нагрузочными резисторами. Все 12 схем электрически изолированы друг от друга. Все межэлементные соединения, указанные на рис. 1, выполняются фирмой-изготовителем ИС. Они формируются в виде однослойного печатного монтажа. Сверху наносится изоляционная маска из стекла или SiO₂ таким образом, чтобы через ее "окна" были открыты контактные площадки ДТЛ-схем. Второй слой межэлементных соединений проектирует и наносит фирма-потребитель ИС.

Рис. 1. Не полностью "собранная" логическая схема.

Сущность второго метода сводится к переключению отдельных участков схемы с помощью электронных ключей. Внешние выводы ключей всегда находится под управляющим потенциалом. Этот метод еще не

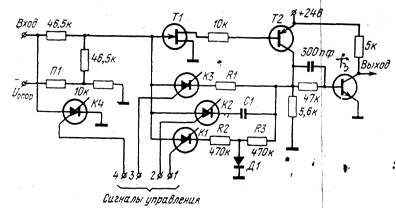доведен до промышленного применения. Проиллюстрируем его на примере схемы детектора уровня, изображенной на рис. 2.

Рис. 2. Схема с перестраиваемой структурой.

В схеме предусмотрены четыре p—n—p—n-переключателя, подключающих или отключающих Основные элементы и участки схемы. Сигналы на управляющие электроды переключателей подаются от внешних цепей. При включении только переключателя Кл1 схема работает следующим образом. Положительный входной сигнал вместе с опорным напряжением, снимаемым с делителя П1, подается на затвор полевого транзистора 77. При достижении потенциала насыщения полевой транзистор открывается и включает в работу обычный биполярный транзистор Т2, который в свою очередь открывает диод Д1. В результате на вход схемы через цепь о. с. подается небольшой по величине синфазный сигнал. Величину этого сигнала (коэффициент обратной связи) и запаздывание схемы можно регулировать, изменяя сопротивление цепи обратной связи, в частности R2. Выбирая это сопротивление достаточно большим, мы устанавливаем режим работы детектора уровня. Транзистор ТЗ согласует схему с нагрузкой. При включении только переключателя КлЗ (вместо цепочки R2, R3, Д1 включается R1) схема работает как бистабильный мультивибратор, запускаемый знакопеременной последовательностью импульсов. При включении только переключателя Кл2 (вместо R1 включается С1) и подаче на вход стробирующих сигналов схема работает как генератор стробов. При одновременном включении Кл2 и Kл4 (вход заземляется), а также при определенном подборе опорного напряжения U_оп схема работает как мультивибратор.

На этапе анализа параметров электрическая схема — модель исследуется как аналитически, так и экспериментально. В процессе анализа уточняются ее внешние параметры и характеристики и определяются количественные зависимости изменений этих параметров и характеристик от вариации параметров элементов схемы^*. Анализ обычно проводится методами граничных испытаний , частичных испытаний, наихудшего случая, математического моделирования на ЭВМ (1.48, и другими методами.

Особенности экспериментального моделирования.

Прежде всего вызывает затруднение практическая ограниченность вариации параметров схемных элементов. Если резисторы, емкости и индуктивности, параметры которых должны изменяться в заданном диапазоне величин, можно отразить в схеме соответственно потенциометрами, конденсаторами переменной емкости и вариометрами, то гипотетический транзистор с переменными параметрами не имеет практического аналога. Поэтому в процессе эксперимента одни транзисторы (а также другие элементы с нерегулируемыми параметрами) постоянно заменяются в схеме на другие, параметры которых отличаются нужным образом от первых. Это обстоятельство снижает гибкость эксперимента и увеличивает его трудоемкость.

Исследуемая схема-модель должна как можно точнее отражать реальную ИС. Для этого необходимо, во-первых, чтобы элементы схемы-модели были бы точными аналогами соответствующих элементов ИС и, во-вторых, чтобы электрические связи в схеме-модели точно отражали бы связи соответствующих элементов ИС. Реально ни первое, ни второе требование полностью не удовлетворяются, особенно для монолитных (полупроводниковых) ИС.

Резисторы, конденсаторы и транзисторы ИС обладают специфическими паразитными параметрами. В частности, полупроводниковые диффузионные резисторы и конденсаторы имеют паразитную емкость относительно подложки, величина которой зависит от напряжения обратного смещения. Эта паразитная емкость носит распределенный характер и замена её дискретной емкостью является известным приближением. То же самое относится ко всём паразитным ёмкостями, образуемым изолирующими переходами.

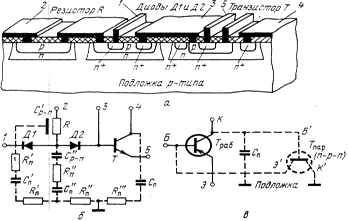
Рис. 3.Участок полупроводниковой ИС (а), его упрощённая эквивалентная электрическая схема (б), условная эквивалентная схема интегрального транзистора с изолирующим p—n-переходом (в).

Планарный транзистор полупроводниковой ИС часто электрически изолируется от других элементов p—n-переходом (см. рис. 3, а). В итоге транзисторная структура получается четырехслойной с тремя p—n-переходами. Эквивалентная схема такой структуры отражает два транзистора: рабочий и "паразитный". Паразитный транзистор в одних случаях улучшаёт импульсные параметры рабочего транзистора, уменьшая накопленный заряд, а в других случаях (в схемах с непосредственными связями) ухудшает их, увеличивая сдвиг входных характеристик при насыщении. Естественно, что указанные ограничения уменьшают гибкость эксперимента. В качестве иллюстрации к сказанному на рис. 3, б, в приведены принципиальная схема участка полупроводниковой ИС и его упрощенная эквивалентная схема. В схеме транзистор T_раб, резистор R и два диода Д1 и Д2 являются основными или рабочими элементами, а транзистор Т_пар — паразитным. Емкости С_п, С^’_п и С^”_п п между подложкой и n-слоем транзисторной, резисторной и диодных структур, а также ёмкости С^'_p—n и С^”_p—n между n- и p-слоями резисторной и диодных структур, сопротивления R^'_п и R^”_п n-слоев и сопротивления R^'_п, R^”_п и R^”’_п подложки являются паразитными элементами. Ёмкость С^'_p—n имеет распределённый характер.

Математическое моделирование.

Теоретический анализ или моделирование схем обычно производится с помощью ЭВМ. Анализ состоит из следующих последовательных этапов: формализация схемы, составление ее математической модели, разработка алгоритма и программы моделирования, процесс моделирования работы схемы на вычислительной машине, исследование полученных данных. При формализации реальную схему заменяют ее более упрощенным эквивалентом, отражающим главные исследуемые свойства реальной схемы. Математическая модель схемы, как правило, отражает систему дифференциальных уравнений, описывающих протекающие в схеме электрические процессы, а также ограничения, выраженные в виде равенств, неравенств, числовых коэффициентов и т. п.

Алгоритм составляется независимо от конкретного типа вычислительной машины. Программа моделирования работы схемы обычно содержит ряд типовых подпрограмм, отражающих моделирование отдельных сложных элементов (транзисторов и др.). К программе предъявляются требования универсальности, возможности применения для моделирования широкого класса схем, удобства вмешательства на разных этапах моделирования и компактности выдачи конечных результатов. Составление больших программ является сложным и трудоемким процессом.

В настоящее время разработаны стандартные программы моделирования электронных схем на ЭВМ. Примерами таких программ могут служить ПАЭС (программа анализа электронных схем) и "Фрехта" (программа расчета и анализа частотных характеристик линейных аналоговых схем).

В программе ПАЭС предусматривается расчет переходных процессов схемы, статистический анализ статических и динамических характеристик схемы и расчет схемы на предельный случай. В ее состав входит внешняя программа-диспетчер, цифровая модель схемы и комплекс подпрограмм цифрового моделирования. Общая структура ПАЭС представлена на рис. 4. В ПАЭС входит серия типовых подпрограмм: подпрограммы расчета параметров нелинейных элементов (транзистора, диода и др.), подпрограммы определения входных импульсов и выходных параметров различного класса схем, подпрограмма интегрирования дифференциальных уравнений по методу Эйлера с автоматическим выбором шага интегрирования, подпрограмма выработки случайных чисел и другие. Включение в работу тех или иных подпрограмм в нужной последовательности, показанной на рис. 4 строками, осуществляется внешней программой. Для типовых алгоритмов анализа схем определенного класса ведущая программа остается неизменной. Автоматизация программирования с помощью создания подпрограмм упрощает процесс подготовки задачи к решению и позволяет более экономно использовать емкость памяти машины. Цифровая модель программируется заново для каждой конкретной схемы.

Процесс получения математической модели схемы в виде системы дифференциальных уравнений несложен; он состоит из ряда формальных процедур, описанных в литературе. Рассмотрим порядок получения математической модели транзистора, используемой при цифровом моделировании интегральных схем. Все существующие его модели получены на основе использования известных уравнений непрерывности и переноса, а также принятия ряда известных допущений.

Рис 4. Общая структура ПАЭС (программы анализа электронных схем)

Эквивалентная схема p—n—p-транзистора приведена на рис. 5. Этой схеме соответствует следующая система дифференциальных уравнений:

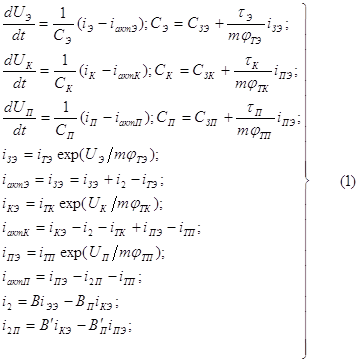
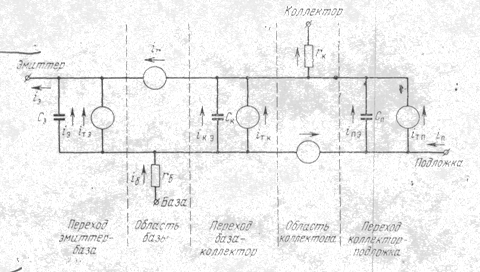
Рис. 5. Эквивалентная схема транзистора.

Индексы "э", "к" и "п" относят соответствующую величину к переходу эмиттер—база, коллектор—база и подложка—коллектор; — падение напряжения на переходе; — выходной ток транзистора; — активная составляющая тока через переход; — емкость перехода, включающая зарядную и диффузионную составляющие;, , , —тепловые токи переходов; , , —температурные потенциалы переходов; , , — зарядные емкости переходов; , , , — коэффициенты передачи тока соответственно от эмиттера к коллектору, от коллектора к эмиттеру, от базы к подложке и от подложки к базе; , , — постоянные времени переходов; и — объемные сопротивления базы и коллектора.

При численном интегрировании системы уравнений (1) токи определяются на каждом шаге интегрирования из уравнений, описывающих схему, в состав которой входит транзистор. Емкости и активные составляющие токов переходов зависят от напряжений на переходах, вычисленных на предыдущем шаге; и от параметров транзистора.

Взаимосвязь подпрограмм моделирования нелинейных элементов с общей программой ПАЭС вытекает из следующего. Для двухполюсника, изображенного на рис. 6, при численном интегрировании системы дифференциальных уравнений на i-м.шаге

. (2)

Определение не связано с решением уравнений, описывающих процессы в активной части двухполюсника A, а определение не связано с решением уравнений внешней цепи. Это и обусловливает возможность определения с помощью основной программы (а также задание этого тока как входной величины для подпрограммы моделирования двухполюсника А). В соответствии с этим эквивалентную схему транзистора можно свести к совокупности трех двухполюсников (по числу переходов), зашунтированных емкостями переходов и сопротивлениями и . Если исключить из эквивалентной схемы двухполюсники А, то мы получим схему замещения транзистора, изображенную на рис. 7. При подготовке к моделированию схемы транзистор представляется схемой замещения и программируются только формулы для вычисления . Затем программируется обращение к подпрограмме транзистора, в которой вычисляются и напряжение

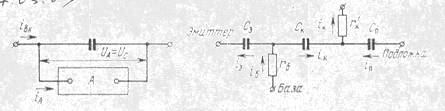Рис. 6. Схема двухполюсника. Рис. 7. Схема замещения

транзистора

Оптимизация схемы (модели).

На основании анализа результатов моделирования схему оптимизируют. В нашем распоряжении имеется семейство зависимостей выходных характеристик схемы от вариации параметров ее элементов. В качестве примера на рис. 8 показано изменение зоны разброса передаточной характеристики типовой логической схемы в зависимости от вариации параметров ее элементов, где — минимальное напряжение логической "единицы"; — максимальное напряжение логического "нуля"; — максимально допустимое напряжение логического "нуля" на входе, при котором на выходе сохраняется логический "нуль". Величина управляющего напряжения ограничена полушириной запрещённой зоны 0,6 эВ (Si); 0,7 эв (GaAs); 0,4 эВ (Ga) из-за протекания прямого тока через затвор в область канала.

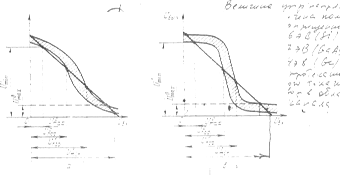
Рис. 8. Зона разброса передаточной характеристики логической схемы.

Границы зоны разброса передаточной характеристики соответствуют наихудшему случаю вариации параметров (величина, знак, вероятность распределения) элементов схем, изменить который мы не можем, так как нам заданы технологический разброс, диапазон изменения параметров внешней среды (температуры), зависимости старения материалов. Предположим, что полученный разброс параметров передаточной характеристики нас не удовлетворяет (не соответствует техническому заданию). Тогда мы вынуждены последовательно изменять номинал элементов схемы, в отдельных случаях и ее структуру для достижения удовлетворительного разброса. Каждое указанное изменение сопровождается циклом расчетного моделирования на машине. Результаты расчетов непрерывно сравниваются с контрольными параметрами (в данном случае — с величиной разброса напряжений), и при достижении удовлетворительного решения оптимизация схемы прекращается. На рис. 1.24, б показан такой случай. Однако в результате оптимизации схемы увеличилась ее нелинейность. Следует отметить, что при проектировании ИС любых типов стремятся построить их таким образом, чтобы они работали с максимально возможным разбросом параметров элементов при сохранении внешних характеристик в допустимых пределах. Выполнение этого условия тесно связано с величиной производственного брака при изготовлении ИС: чем больше допустимый разброс параметров элементов, тем меньше брака и ниже стоимость ИС^*.

Однако улучшение выходных характеристик системы с помощью ее оптимизации не всегда связано с проблемой допусков. В ряде случаев необходимо улучшить такие параметры схемы, как надежность, чувствительность, избирательность, устойчивость, помехозащищенность и др. Из-за сложности решения задач оптимизации обычно выбирают один или два таких критерия, придавая неопределенные весовые (удельные) значения. Одновременно с этим выбирают ограничения оптимизации (допустимый разброс параметров элементов, напряжения питания, однородность схемы и др.). На основе математической модели схемы составляют так называемую целевую функцию, представляющую зависимость оптимизируемого внешнего параметра схемы от параметров ее элементов. Целевая функция моделируется на ЭВМ. Как и при расчете допусков, последовательно изменяются сначала параметры элементов схемы, а затем в случае необходимости и сама структура схемы.

ЛИТЕРАТУРА

1. Петров К.С. Радиоматериалы, радиокомпоненты и электроника: Учебное пособие для вузов. – СПб: Питер, 2003. – 512 с.

2. Опадчий Ю.Ф. и др. Аналоговая и цифровая электроника: Учебник для вузов / Ю.Ф.Опадчий, О.П.Глудкин, А.И.Гуров; Под.ред. О.П.Глудкина. М.: Горячая Линия – Телеком, 1999. – 768 с.

3. Акимов Н.Н. и др. Резисторы, конденсаторы, трансформаторы, дроссели, коммутационные устройства РЭА: Справочник / Н.Н.Акимов, Е.П.Ващуков, В.А.Прохоренко, Ю.П.Ходоренок. Мн.: Беларусь, 2004. – 591 с.