Парная регрессия
Контрольная работа
по теме: "Парная линейная регрессия"
Данные, характеризующие прибыль торговой компании "Все для себя" за первые 10 месяцев 2004 года (в тыс. руб.), даны в следующей таблице:
| январь | февраль | март | апрель | май | июнь | июль | август | сентябрь | октябрь |
| 367 | 418 | 412 | 470 | 485 | 470 | 525 | 568 | 538 | 558 |
В контрольной работе с использованием табличного процессора Ехсеl необходимо выполнить следующие вычисления и построения:
1. Построить диаграмму рассеяния.
2. Убедится в наличии тенденции (тренда) в заданных значениях прибыли фирмы и возможности принятия гипотезы о линейном тренде.
3. Построить линейную парную регрессию (регрессию вида ![]() ). Вычисление коэффициентов 0, 1 выполнить методом наименьших квадратов.
). Вычисление коэффициентов 0, 1 выполнить методом наименьших квадратов.
4. Нанести график регрессии на диаграмму рассеяния.
5. Вычислить значения статистики F и коэффициента детерминации R2. Проверить гипотезу о значимости построенного уравнения регрессии.
6. Вычислить выборочный коэффициент корреляции и проверить гипотезу о ненулевом его значении.
7. Вычислить оценку дисперсии случайной составляющей эконометрической модели.
8. Проверить гипотезы о значимости вычисленных коэффициентов 0, 1 .
9. Построить доверительные интервалы для коэффициентов 0, 1.
10. Построить доверительные интервалы для дисперсии случайной составляющей эконометрической модели.
11. Построить доверительную область для условного математического ожидания М(![]() )( по оси Х откладывать месяцы январь - декабрь). Нанести границы этой области на диаграмму рассеяния.
)( по оси Х откладывать месяцы январь - декабрь). Нанести границы этой области на диаграмму рассеяния.
12. С помощью линейной парной регрессии сделать прогноз величины прибыли на ноябрь и декабрь месяц и нанести эти значения на диаграмму рассеяния. Сопоставить эти значения с границами доверительной области для условного математического ожидания М(![]() ) и сделать вывод о точности прогнозирования с помощью построенной регрессионной модели.
) и сделать вывод о точности прогнозирования с помощью построенной регрессионной модели.
Решение.
Используя исходные данные, строим диаграмму рассеяния:
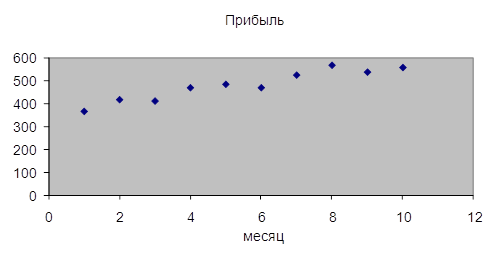
На основе анализа диаграммы рассеяния убеждаемся в наличии тенденции увеличения прибыли фирмы и выдвигаем гипотезу о линейном тренде.
Полагаем, что связь между факторами Х и У может быть описана линейной функцией ![]() . Решение задачи нахождения коэффициентов 0, 1 основывается на применении метода наименьших квадратов и сводится к решению системы двух линейных уравнений с двумя неизвестными 0, 1 :
. Решение задачи нахождения коэффициентов 0, 1 основывается на применении метода наименьших квадратов и сводится к решению системы двух линейных уравнений с двумя неизвестными 0, 1 :
0n + 1 Уxi = Уyi,
0 Уxi + 1 Уxi2 = Уxiyi.
Составляем вспомогательную таблицу:
| № | х | y | x2 | ху | y2 |
| 1 | 1 | 367 | 1 | 367 | 134689 |
| 2 | 2 | 418 | 4 | 836 | 174724 |
| 3 | 3 | 412 | 9 | 1236 | 169744 |
| 4 | 4 | 470 | 16 | 1880 | 220900 |
| 5 | 5 | 485 | 25 | 2425 | 235225 |
| 6 | 6 | 470 | 36 | 2820 | 220900 |
| 7 | 7 | 525 | 49 | 3675 | 275625 |
| 8 | 8 | 568 | 64 | 4544 | 322624 |
| 9 | 9 | 538 | 81 | 4842 | 289444 |
| 10 | 10 | 558 | 100 | 5580 | 311364 |
| сумма | 55 | 4811 | 385 | 28205 | 2355239 |
Для нашей задачи система имеет вид:
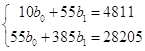
Решение этой системы можно получить по правилу Крамера:
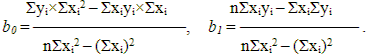
Получаем:
![]() ,
, ![]() .
.
Таким образом, искомое уравнение регрессии имеет вид:
y =364,8 + 21,145x.
4. Нанесем график регрессии на диаграмму рассеяния.
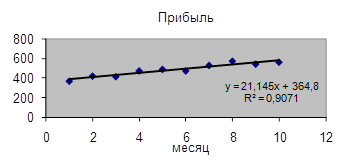
5. Вычислим значения статистики F и коэффициента детерминации R2. Коэффициент детерминации рассчитаем по формуле R2 = rxy2= 0,9522 = 0,907. Проверим адекватность модели (уравнения регрессии) в целом с помощью F-критерия. Рассчитаем значение статистики F через коэффициент детерминации R2 по формуле:
![]()
Получаем: ![]() . Зададим уровень значимости б =0,01, по таблице находим квантиль распределения Фишера F0,01;1;8 = 11,26, где 1 – число степеней свободы.
. Зададим уровень значимости б =0,01, по таблице находим квантиль распределения Фишера F0,01;1;8 = 11,26, где 1 – число степеней свободы.
Fфакт. > F0,01;1;8, т.к. 78,098 > 11,26.
Следовательно, делаем вывод о значимости уравнения регрессии при 99% - м уровне значимости.
6. Вычислим выборочный коэффициент корреляции и проверим гипотезу о ненулевом его значении.
Рассчитаем выборочный коэффициент корреляции по формуле:
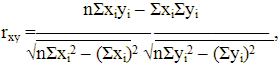
Получаем:
![]()
Проверка существенности отличия коэффициента корреляции от нуля проводится по схеме:если 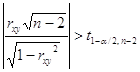 , то гипотеза о существенном отличии коэффициента корреляции от нуля принимается, в противном случае отвергается.
, то гипотеза о существенном отличии коэффициента корреляции от нуля принимается, в противном случае отвергается.
Здесь t1-б/2,n-2 – квантиль распределения Стьюдента, б - уровень значимости или уровень доверия, n – число наблюдений, (n-2) – число степеней свободы. Значение б задается. Примем б = 0,05, тогда t1-б/2,n-2 = t0,975,8 = 2,37. Получаем:
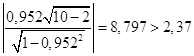 .
.
Следовательно, коэффициент корреляции существенно отличается от нуля и существует сильная линейная связь между х и у.
С использованием табличного процессора Ехсеl проведем регрессионную статистику:
Вывод итогов:
| Регрессионная статистика | |
| Множественный R | 0,952409 |
| R-квадрат | 0,907083 |
| Нормированный R-квадрат | 0,895468 |
| Стандартная ошибка | 21,7332 |
| Наблюдения | 10 |
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 1 | 36888,245 | 36888,25 | 78,09816 | 2,119E-05 |
| Остаток | 8 | 3778,6545 | 472,3318 | ||
| Итого | 9 | 40666,9 | |||
| Коэфф. | Станд. ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 364,8 | 14,846599 | 24,57128 | 8,04E-09 | 330,56368 | 399,0363 |
| Переменная X 1 | 21,14545 | 2,3927462 | 8,837316 | 2,12E-05 | 15,627772 | 26,66314 |
Вычисленные значения коэффициентов 0, 1,значения статистики F, коэффициента детерминации R2 выборочного коэффициента корреляции rxy совпадают с выделенными в таблице.
7. Оценка дисперсии случайной составляющей эконометрической модели вычисляется по формуле ![]() .
.
Используя результаты регрессионной статистики, получаем:
![]() .
.
8. Проверим значимость вычисленных коэффициентов 0, 1 по t-критерию Стьюдента. Для этого проверяем выполнение неравенств:
![]() и
и ![]() ,
,
где
![]() ,
, ![]() ,
, 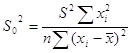 ,
, 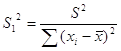 .
.
Используем результаты регрессионной статистики:
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 364,8 | 14,846599 | 24,57128 | 8,04E-09 | 330,56368 | 399,0363 |
| Переменная X 1 | 21,14545 | 2,3927462 | 8,837316 | 2,12E-05 | 15,627772 | 26,66314 |
Получаем: ![]() ;
; ![]() Примем б = 0,05, тогда t1-б/2,n-2 = t0,975,8 = 2,37.
Примем б = 0,05, тогда t1-б/2,n-2 = t0,975,8 = 2,37.
Так как ![]() и
и ![]() , делаем вывод о значимости коэффициентов линейного уравнения регрессии.
, делаем вывод о значимости коэффициентов линейного уравнения регрессии.
9. Доверительные интервалы для коэффициентов 0, 1 получаем с помощью результатов регрессионной статистики.
Доверительный интервал для коэффициента 0 уравнения регрессии:
![]()
Доверительный интервал для коэффициента 1 уравнения регрессии:
![]()
10. Построим доверительный интервал для дисперсии случайной составляющей эконометрической модели по формуле:
![]() .
.
Примем б = 0,05, тогда по таблице для 10-элементной выборки q= 0,65.
Получаем:
![]() ,
,
![]() .
.
11. Построим доверительную область для условного математического ожидания М(![]() ).
).
Доверительные интервалы для уравнения линейной регрессии: ![]() находятся по формуле:
находятся по формуле:
![]()
где ![]() соответственно верхняя и нижняя границы доверительного интервала;
соответственно верхняя и нижняя границы доверительного интервала; ![]() значение независимой переменной
значение независимой переменной ![]() для которого определяется доверительный интервал,
для которого определяется доверительный интервал, ![]() квантиль распределения Стьюдента,
квантиль распределения Стьюдента, ![]() доверительная вероятность, (n-2) – число степеней свободы;
доверительная вероятность, (n-2) – число степеней свободы;
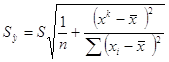
![]()
Рассмотрим уравнение: y =364,8 + 21,145x. Пусть ![]() тогда
тогда ![]() . Зная
. Зная ![]() и
и ![]() , заполним таблицу:
, заполним таблицу:
|
|
|
|
|
|
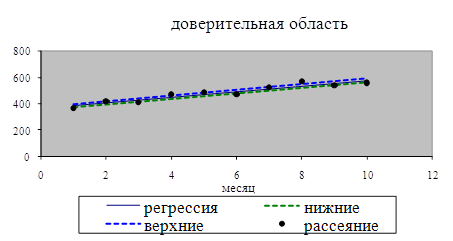
| 1 | 385,95 | 20,25 | 4,634 | 377,327 | 394,564 |
| 2 | 407,09 | 12,25 | 5,215 | 397,391 | 416,791 |
| 3 | 428,24 | 6,25 | 5,738 | 417,564 | 438,908 |
| 4 | 449,38 | 2,25 | 6,217 | 437,819 | 460,945 |
| 5 | 470,53 | 0,25 | 6,661 | 458,138 | 482,917 |
| 6 | 491,67 | 0,25 | 7,078 | 478,508 | 504,838 |
| 7 | 512,82 | 2,25 | 7,471 | 498,921 | 526,715 |
| 8 | 533,96 | 6,25 | 7,845 | 519,372 | 548,556 |
| 9 | 555,11 | 12,25 | 8,202 | 539,854 | 570,365 |
| 10 | 576,25 | 20,25 | 8,544 | 560,363 | 592,146 |
| сумма | 82,5 | ||||
| 11 | 597,4 | 30,25 | 8,873 | 580,897 | 613,903 |
| 12 | 618,55 | 42,25 | 9,190 | 601,453 | 635,638 |
График уравнения регрессии, доверительная полоса, диаграмма рассеяния:
12. С помощью линейной парной регрессии сделаем прогноз величины прибыли на ноябрь и декабрь месяц:
![]() 597,4,
597,4, ![]() 618,55.
618,55.
Нанесем эти значения на диаграмму рассеяния.
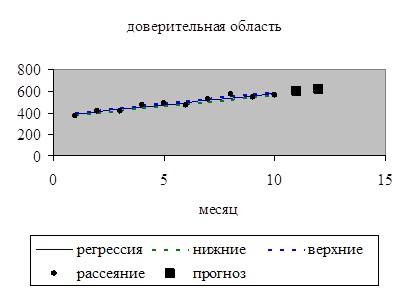
Эти значения сопоставимы с границами доверительной области для условного математического ожидания М(![]() ).
).
Точность прогнозирования: с вероятностью 0,95 прибыль в ноябре находится в интервале (487,292; 515,508); прибыль в декабре находится в интервале (497,152; 526,376).