Доказательство Великой теоремы Ферма с помощью метода бесконечных (неопределенных) спусков

Доказательство Великой теоремы Ферма

с помощью метода бесконечных (неопределенных) спусков

§1.

Решение задач в науке определяется верифицированным методом доказательства. Как мы видим из разнообразной литературы по проблеме решения Великой теоремы Ферма неразличение исторических счастливых случайных, и оттого многообразных, находок и логических т.е. теоретических нормальных закономерных изобретений сделало из числового уравнения задачу «икс» для многих поколений математиков.

Анализ монографий и учебников по самым различным наукам и, в том числе, т.н. математическим показывает, что представление наук «об их предмете» является самым слабым звеном. Затем идет «представление о методе», о «научном законе» и «языке науки».

Как соотносится решение конкретной задачи с представлением наук о предмете, методе, научном законе и языке конкретной науки? Обычно этим вопросом никто и не задается. Но первое же действие по решению задачи привело автора к необходимости определиться, узнать, с помощью какой науки или совокупности наук надо подойти к решению задачи, какой инструмент необходим? При нынешнем плюрализме в науках уже одно это занятие ставит исследователя в неловкое положение. Что говорить, если даже из предмета т.н. точных, математических наук явно не увидеть явно то, чем занимается наука (предмет науки).

Условия задачи указывают на необходимость привлечения к исследованию науки о числах и науки о действиях с числами (и в общем виде с величинами). С наукой о числах больших проблем не возникло, это область теории чисел, но вот то, что действие с числами это предмет алгебры – может догадаться только очень искушенный в т.н. математических трудах исследователь. И то неявно. Недоумение вызвал и тот факт, что понятие границ величины автор так и не нашел. Т.е. как математики отличают величину от не-величны в явном виде автор так и не смог определить (для себя принял условие, что границы величины должны быть несоизмеримы с величиной и выражаются нулевым числом т.е. они могут соизмеряться с величиной, но должны быть меньше самой малой дискретной меры величины).

Сама математика при изучении ее фактического материала представляется автору, скорее, в виде научной дисциплины по созданию моделей с определенными (описанными) величинами, которая использует закономерности всего круга т.н. математических наук.

Вместе с тем, гипотеза Ферма, доказать которую мы беремся в данной работе, сформулирована таким образом, что указывает нам на необходимость привлечения еще и науки о геометрических формах и представлениях числа.

В настоящей статье предлагается использовать теоретико-числовой и алгебраический метод доказательства, с наглядной геометрической верификацией, который был изобретен П.Ферма, автором Великой гипотезы (и как мы увидим далее - теоремы), названной в его честь. Изобретенный им метод доказывания, называемый методом бесконечных (неопределенных) спусков основан на интеллектуальной возможности производить определенные (имеющие свойства) действия с существующими числами и действительными числовыми выражениями.

Этот математический метод П. Ферма описывал в своем письме к Каркави (август 1659 года) следующим образом:

«Если бы существовал некоторый прямоугольный треугольник в целых числах, который имел бы площадь, равную квадрату, то существовал бы другой треугольник, меньший этого, который обладал бы тем же свойством. Если бы существовал второй, меньший первого, который имел бы то же свойство, то существовал бы, в силу подобного рассуждения, третий, меньший второго, который имел бы то же свойство, и, наконец, четвертый, пятый, спускаясь до бесконечности. Но если задано число, то не существует бесконечности по спуску меньших его (я все время подразумеваю целые числа). Откуда заключают, что не существует никакого прямоугольного треугольника с квадратной площадью».

Дано утверждение (в лексике П.Ферма(1)):

«Нельзя разложить куб на два куба, ни квадрато-квадрат (т. е. четвертую степень числа) на два квадрато-квадрата, ни вообще никакую степень выше квадрата и до бесконечности нельзя разложить на две степени с тем же показателем». Далее автор утверждения – П.Ферма делает заметку: «Я открыл этому поистине чудесное доказательство, но эти поля (имеется ввиду книги которую он читал книги – авт.) для него слишком узки».

«Наоборот, невозможно разложить ни куб на два куба, ни биквадрат на два биквадрата и вообще ни в какую степень, большую квадрата, на две степени с тем же показателем».

На современном математическом языке.

Дано: уравнение aⁿ + ⁿ = cⁿ при натуральном⊂N, n > 2,не имеет решения в ненулевых целых числах а’ , ’, c’ ,{a’, ’, c’}⊂ Z .

Доказательство:

Рассмотрим метод бесконечных (неопределенных) спусков, который мы собираемся применить для доказательства.

Дано уравнение:a² + ² = c²;

Решения данного уравнения выражаются в следующей геометрической форме:прямоугольный треугольник с катетами a , и гипотенузойc.

Предположим, что уравнение a² + ² = c² имеет решение в целых числах a', ’, c’

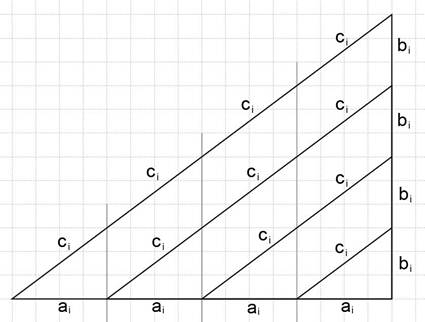
Метод бесконечного (неопределенного) утверждает, что если существует прямоугольный треугольник со сторонами a', ’, c’ выраженным в натуральных числахто, будет существовать бесконечное число прямоугольных треугольников имеющих стороны:

aпропорционально a’ ,

пропорционально ’,

cпропорционально c’,

Т.е. если есть решение уравнения (существует треугольник a', ’, c’) то мы можем найти бесконечное пропорциональное количество решений уравнения

a² + ² = c²

где

a_i = k_i· а’ ;

b_i = k_i·b’;

c_i = k_i·c’;

где к – любое действительное число, аi - произвольный нумератор решений множества решений

Iсостоящее из решений совокупности связанных решений (a_i, b_{i ,} c_i) определяемых через любое существующее решение (a’,’,c’) .

Таким образом, i -тое решение уравнения a² + ² = c² позволяет нам найти определить I -тое коммутативное множество решений уравнения.

Принципиальная невозможность решения уравнения a² + ² = c² позволяет нам утверждать невозможности получения всего множества решений уравнения.

Верификация метода бесконечных (неопределенных) спусков:

Стороны уравнения a² + ² = c² в силу закона ассоциативности могут быть умножены на любое рациональное число К выраженное через действительное число к в виде К = к ²: мы можем сделать преобразование и в целых числах a', ’, c’ представить уравнение a² + ² = c² выражением в виде:

К · (a’ ² + ’ ²) = К · c’ ²

в силу закона дистрибутивности (или распределительности) можно сделать следующее преобразование и получить выражение в виде:

K·a’² + K· ’² = K· c’²

где К – любое рациональное число и К = к ² где к – любое действительное числоследующее преобразование приводит уравнение

aⁿ + bⁿ = cⁿк виду:

k²a² + k²b² = k²c²

(ka)² + (kb)² = (kc)²

где К – любое рациональное число K∈ { Q },где Q – поле рациональных чисел, образованное из действительного числа k по формуле К = k^{2 ,} где число k ∈ { R },где R – поле действительных чисел

Действительное число к множества действительных чисел – позволяет работать во всем действительном числовом поле решений, представленных в виде (k_ia’, k_ib’, k_ic’) даже при единственном возможном решении где a', ’, c’ – целые числа

Множество всех действительных чисел составляют натуральные, целые, рациональные и иррациональные числа

N ⊂ Z ⊂ Q ⊂ R , J⊂ R решения { k_ia’, k_ib’, k_ic’ } ⊂R.

Это значит, что если не существует решения a² + ² = c² (a', ’, c’) не существует и ни одного решения (k_ia’, k_ib’, k_ic’) во всем множестве целых чисел

(a, , c)⊂ Z

Верификация метода бесконечных (неопределенных) спусков в геометрическом виде представлена(2) на рис. 1: