Дисциплины обслуживания вызовов. Простейшая модель обслуживания
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Кафедра сетей и устройств телекоммуникаций
РЕФЕРАТ
На тему:
«Дисциплины обслуживания вызовов. Простейшая модель обслуживания»
Минск, 2008
Дисциплины обслуживания вызовов
Поступающие потоки сообщений могут обслуживаться без потерь и с потерями. В первом случае для передачи каждого сообщения немедленно представляется требуемое соединение, а вот втором – часть сообщений получает отказ в обслуживании, или обслуживание их задерживается на некоторое время.
Обслуживание с явными потерями предполагает, что сообщение и соответствующий ему вызов при получении отказа в немедленном соединении полностью теряются и на обслуживание больше не поступают.
Обслуживание с условными потерями предполагает, что большинство вызовов получает немедленное обслуживание, а другие обслуживаются с задержкой сверх допустимого срока.
Обслуживание с условными потерями может быть организовано по системе с ожиданием соединения и с повторными вызовами.
 |
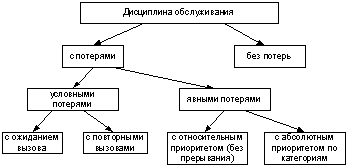На практике целесообразно использовать обслуживание с потерями для систем с коммутацией каналов (рис. 1).
Рис. 1 Классификация дисциплин обслуживания
Модель с явными потерями
На вход КС поступает входящий поток вызовов, к выходам подключаем пучок исходящих линий емкостью 
, это означает, что одновременно система может обслужить только входящих вызовов (рис. 2).
Рис.5 Модель с потерями
Если через 
обозначить число вызовов, находящихся на обслуживании в момент 
, то данную дисциплину обслуживания с потерями можно описать так: поток вызовов, поступающий в состоянии , причем 
, получает немедленное обслуживание.
При 
вызов получает отказ и больше на обслуживание не поступает. Вызов и связанное с ним информационное сообщение теряются.
Характеристики качества обслуживания
Для систем с явными потерями качество обслуживания оценивается с помощью вероятности потерь сообщений. Различают потери по времени (
) и потери по вызовам (
).
Вероятность потерь по вызовам 
- это отношение математического ожидания, потерянных вызовов 
к математическому ожиданию поступивших 
.
Вероятность потерь по вызовам совпадает с вероятностью явной потери поступившего сообщения.
Вероятность потерь по времени 
характеризует вероятность занятости всех доступных данному источнику соединительных путей требуемых в данном направлении.
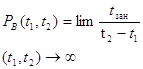
На практике потери по времени определяют как долю конечного интервала наблюдения 
в течение которой заняты все каналов обслуживания:
Таким образом характеризует потенциальную возможность потери вызова в промежутке 
.
Как связаны эти 2 две величины и ?
Рассмотрим систему с N ресурсами (соединительных линий, каналов). Измерим время, в течение которого все ресурсы заняты, и отнесем к рассматриваемому периоду. Это может быть числом минут (или секунд) в данном часе, когда заняты все линии. Эта доля дает оценку вероятности того, что все N ресурсов заняты, которая и является вероятностью потерь по времени или вероятностью блокировки системы - .
В качестве другой возможной меры перегрузки подсчитаем общее число вызовов, поступающих в течение достаточно длительного промежутка времени, и отметим те из них, которые оказались потерянными из-за нехватки ресурсов. Вызовы теряются, если в момент его поступления все N исходящих каналов оказались занятыми. Отношение числа потерянных вызовов к их общему числу, поступивших в течение времени наблюдения, дает оценку вероятности потерь , или потерь по вызовам.
Для того чтобы связать эти две величины, воспользуемся следующим подходом.
Пусть 
- условная вероятность того, что вызов поступает, когда система заблокирована (т.е. все N каналов заняты). Пусть 
- безусловная вероятность поступления вызова. Вероятность поступления вызова , умноженная на вероятность того, что поступающий вызов застает систему в заблокированном состоянии, должна быть равна вероятности того, что система заблокирована, умноженной на вероятность 
того, что вызов поступает, когда система заблокирована. В результате получаем:
,
Если условная вероятность не зависит от блокирующего состояния системы, т.е. если =, то =.
Пропускная способность системы
Под пропускной способностью коммутационной системы понимается интенсивность обслуженной коммутационной системой нагрузки при заданном качестве обслуживания в рассматриваемый промежуток времени, т.е. вероятности потерь вызовов в системе с явными потерями.
Пропускная способность системы зависит от:
· свойств поступающего потока вызовов;
· закона распределения времени обслуживания;
· структуры, емкости коммутационной системы;
· дисциплины обслуживания;
· нормы качества обслуживания.
Простейшая модель обслуживания
Рассмотрим модель обслуживания, показанную на рис. 3.
Рис. 3 Модель однолинейной системы обслуживания
Вызовы поступают случайным образом со средней интенсивностью 
и обслуживаются со средней скоростью 
. Параметр 
называется средней продолжительностью занятия.
Если интенсивность поступления вызовов приближается к скорости обработки вызовов , то и поступление последующих вызовов будет заблокировано.
Таким образом стабильность работы системы обеспечивается при <. Введем параметр 
- коэффициент использования канала (линии), который определяется как отношение нагрузки системы к ее пропускной способности. Таким образом для существования равновесия необходимо, чтобы интенсивность поступлений или нагрузка системы должна быть меньше ее интенсивности обслуживания , т.е. <1.
Если это условие нарушается, то система не будет работать стабильно.
Модели потока требований
Поступающие на вход системы массового обслуживания требования (заявки, запросы) образуют поток дискретных событий, полностью определяемый множеством моментов времени их поступления 
. Для детерминированного потока значения tn задаются таблицей или формулой. На практике этот поток случайный и значения моментов поступления запросов есть значения случайной величины, задаваемой функциями распределения вероятности tn либо интервала между поступлениями Dt : 
.
В зависимости от вида функции распределения вероятности потоки требований наделяют соответствующими названиями. В общем случае случайные потоки можно классифицировать по наличию или отсутствию трех основных свойств: стационарности, последействия и ординарности.
Стационарность - независимость вероятностных характеристик от времени. Так вероятность поступления определенного числа требований в интервал времени длиной t для стационарных потоков не зависит от выбора начала его измерения.
Последействие - вероятность поступления требований в интервале (t1, t2) зависит от событий, произошедших до момента t1.
Ординарность - вероятность поступления двух и более требований за бесконечно малый интервал времени Δt есть величина бесконечно малая более высокого порядка, чем Δt.
К основным характеристикам случайных потоков относят ведущую функцию, параметр потока и интенсивность потока.
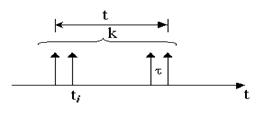
Ведущей функцией потока
называют математическое ожидание числа требований в промежутке времени (0,t).
Параметр потока вместе с интенсивностью потока являются важнейшими характеристиками темпа поступления требований. Это плотность вероятности поступления требований в момент времени t и характеризуется тем, что вероятность поступления хотя бы одного требования в бесконечно малом промежутке времени пропорциональна с точностью до бесконечно малой более высокого порядка длине этого промежутка. 
. Откуда:
.
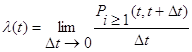Для стационарного потока параметр потока постоянный и равен:
.
Интенсивность потока учитывает возможную неординарность потока, т.е. одновременно поступающие требования и определяется как математическое ожидание числа вызовов в единицу времени в данный момент. Для ординарных потоков интенсивность потока и есть его параметр.
Пуассоновский (простейший) поток запросов
Стационарный ординарный поток без последействия называют простейшим. Он задается набором вероятностей Pi(t) поступления i требований в промежутке длиной t.
Можно показать, что при этих предположениях формула для Pi(t) дается формулой Пуассона (Poisson):
.
Проанализируем основные характеристики пуассоновского потока. Рассмотрим отношение Pi(t)/Pi-1(t). При i ≤ λt вероятность растет, а при обратном соотношении – убывает. Графики функции распределения Пуассона в зависимости от величины λt для различных значений k приведены на рис. 4.
Рис. 4 Графики Пуассоновского распределения в зависимости от lt для различных k.
Наряду с распределением Pi(t) используют вероятности поступления не менее i требований в интервал t или не более i требований за время t:
Если рассмотреть закон распределения вероятностей промежутка между поступлением соседних требований τ, то можно показать, что
.
Дифференцируя, получаем плотность распределения вероятностей: 
.
Случайная величина с такой плотностью вероятностей называется экспоненциально - распределенной (с показательным распределением). Математическое ожидание экспоненциально распределенной случайной величины равно
,
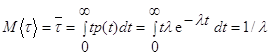а дисперсия и среднеквадратическое отклонение соответственно будут равны:
,
.
Определим математическое ожидание и дисперсию числа требований за промежуток t :
,
.
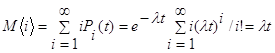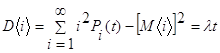Одним из важных свойств пуассоновского потока является аддитивность.
Если образовать поток заявок как объединенный из нескольких пуассоновских потоков, то его суммарная интенсивность будет равна сумме интенсивностей каждого отдельного потока 
.
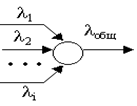
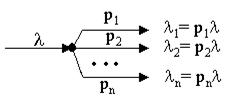
При разъединении пуассоновского потока на несколько потоков так, что каждое требование исходного потока с вероятностью i (Si =1) поступает на i-тоенаправление, поток i направления будет также пуассоновским с интенсивностью l i.
Нестационарный пуассоновский поток
Это ординарный поток без последействия, для которого в любой момент времени существует конечный параметр потока λ(t). Пусть Pi(t0,τ) – вероятность поступления i-требований за интервал (t0,t0+τ), которая определяется формулой:
, где 
.
Этот параметр имеет смысл среднего числа требований на промежутке (t0,t0+τ). Средняя интенсивность определяется как: 
.
Выбором закона изменения λ(t) можно описать реальные потоки заявок на АТС (например, отразить наличие ЧНН).
Стационарный поток без последействия.
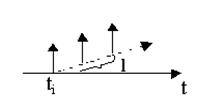
Это неординарный (групповой) пуассоновский поток. События – моменты вызовов, представляют собой простейший пуассоновский поток с параметром λ. В каждый момент времени tiс вероятностью pl поступает группа из l ( l = 1,2,…r) одинаковых заявок. Величинаl– характеристика неординарности. Обозначим параметр al= λpl. Вероятность поступления k требований в промежутке времени длиной t :
.
Суммирование в этой формуле производится по всем j, удовлетворяющим соотношению: 
.
Это означает, что любой неординарный пуассоновский поток можно представить как k независимых неординарных пуассоновских потоков с постоянной характеристикой неординарности l и соответствующими параметром al и интенсивностью lal. Параметр неординарного потока определяется как: 
,
а интенсивность такого потока : 
.
В качестве одного из примеров применения неординарного потока можно привести пуассоновский поток с неординарными заявками, т.е. использующим для своего обслуживания l серверов. В сотовой системе связи в том случае, когда происходит звонок с мобильного телефона на телефоны не расположенные в зоне обслуживания одной базовой станции или на телефоны городской сети, требование обслуживается одним сервером – голосовым каналом, а при осуществлении звонка на мобильный телефон, обслуживаемый одной и той же базовой станцией требуется сразу два сервера – голосовых канала. Следовательно, поток вызовов от мобильных телефонов может рассматриваться как неординарный с характеристикой неординарности равной двум.
Литература
1. Л.Н. Волков, М.С. Немировский, Ю.С. Шинаков. Системы цифровой радиосвязи: базовые методы и характеристики. Учебное пособие.-М.: Эко-трендз, 2005.
2. М.В. Гаранин, В.И. Журавлев, С.В. Кунегин. Системы и сети передачи информации. - М.: Радио и связь, 2001.
3. Н.В. Захарченко, П.Я. Нудельман, В.Г. Кононович. Основы передачи дискретных сообщений. –М.: Радио и связь, 1990.
4. Дж. Прокис. Цифровая связь. - М.: Радио и связь, 2000.
5. Скляр. Цифровая связь. - М.: Радио и связь, 2001.