Конструирование и расчет элементов железобетонных конструкций многоэтажного здания (без подвала) с наружными каменными стенами и внутренним железобетонным каркасом
Федеральное агентство по образованию и науке
Кубанский государственный технологический университет
Кафедра строительных конструкций и гидротехнических сооружений
Пояснительная записка
к курсовому проекту №1
по дисциплине « Железобетонные и каменные конструкции»
На тему:
«Конструирование и расчет элементов железобетонных конструкций многоэтажного здания (без подвала) с наружными каменными стенами и внутренним железобетонным каркасом»
Краснодар 2005г.
1. Компоновка конструктивной схемы сборного перекрытия
Выбираем поперечное расположение ригелей относительно длины здания, за счет чего достигается повышение жесткости, что необходимо в зданиях с большими проемами. На средних опорах ригели опираются на консоли колонн, а по краям заделываются в несущие стены. Принимаем прямоугольную форму сечения ригеля как наиболее простую для расчета.
Исходя из технико-экономического анализа, выбираем продольное расположение плит относительно длины здания, что позволяет в целом сэкономить около двух кубометров железобетона по сравнению с поперечным расположением плит относительно здания.
Поскольку нормативная нагрузка (6,4кПа) больше 5 кПа, принимаем ребристые предварительно напряженные плиты номинальной шириной 1400 мм. Связевые плиты располагаем по рядам колонн. В крайних пролётах помимо основных плит принято по доборному элементу шириной 500 мм.
Принимаем привязку осей 200х310 мм.
В продольном направлении жесткость здания обеспечивается вертикальными связями, устанавливаемыми в одном среднем пролете по каждому ряду колонн.
В поперечном направлении жесткость здания обеспечивается по связевой системе: ветровая нагрузка через перекрытия, работающие как горизонтальные жесткие, передается на торцевые стены, выполняющие функции вертикальных связевых диафрагм, и поперечные рамы. Поперечные же рамы работают на вертикальную и горизонтальную нагрузку.
Исходя из климатических условий района строительства, принимаем толщину стен в два кирпича, то есть 510мм.
Поскольку длина здания больше 40 м, в середине здания в поперечном направлении устраиваем деформационный шов.
2. Расчет ребристой предварительно напряжённой плиты перекрытия по двум группам предельных состояний
2.1 Расчет плиты по предельным состояниям первой группы
2.1.1 Расчетный пролет и нагрузки
Для установления расчетного пролета плиты задаёмся размерами сечения ригеля:
- высота:
![]()
![]()
- ширина:
![]()
![]()
При опирании на ригель по верху расчётный пролёт равен:
![]()
![]()
где ![]() - расстояние между разбивочными осями, м
- расстояние между разбивочными осями, м
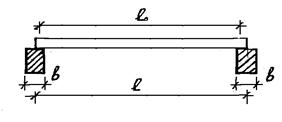 |
Рисунок 2 – К определению расчетного пролета плиты
Таблица 1- Нагрузка на 1м2 междуэтажного перекрытия
| № п/п | Наименование нагрузки | Нормативная нагрузка, Н/м2 | Коэфф. надёжности по нагрузке | Расчётная нагрузка. Н/м2 |
| 1 | Постоянная Собственный вес ребристой плиты:
то же керамических плиток, ИТОГО: | 2450 440 240 | 1,1 1,3 1.1 | 2695 575 265 |
| 3130 | - | 3535 | ||
| 2 | Временная В том числе: Длительная кратковременная | 6400 4480 1920 | 1,2 1,2 1,2 | 7680 5380 2300 |
| 3 | Полная нагрузка В том числе: постоянная и длительная кратковременная | 9530 7610 1920 | - - - | 11215 - - |
Расчётная нагрузка на 1 м при ширине плиты 1,4 м с учётом коэффициента
надёжности по назначению здания![]()
постоянная ![]()
полная ![]()
![]()
![]()
временная ![]()
Нормативная нагрузка на 1 м длины:
постоянная ![]()
полная ![]()
в том числе постоянная и длительная: ![]()
2.1.2 Усилия от расчетных и нормативных нагрузок
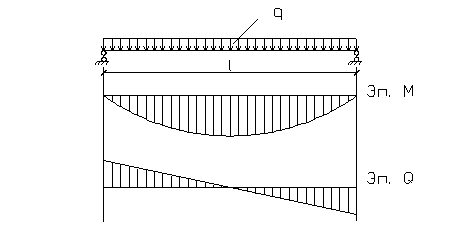
Рисунок 3- Расчетная схема плиты
От расчетной нагрузки:
![]()
![]()
![]()
От нормативной нагрузки:
![]()
![]()
![]()
![]()
От нормативной постоянной и длительной нагрузки:
![]()
![]()
2.1.3 Установление размеров сечения плиты
Высота сечения ребристой предварительно напряженной плиты ![]() .
.
Рабочая высота сечения ![]()
Ширина продольных ребер понизу ![]()
Ширина верхней полки ![]() .
. ![]()
В расчетах по предельным состояниям первой группы расчетная толщина сжатой полки таврового сечения ![]() ; отношение
; отношение ![]() при этом в расчет вводится вся ширина полки
при этом в расчет вводится вся ширина полки ![]() .
.
Расчетная ширина ребра ![]()

a) проектное сечение
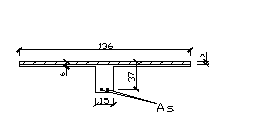
б) приведенное сечение
Рисунок 4- Поперечные сечения ребристой плиты
2.1.4 Характеристики прочности бетона и арматуры
Ребристую предварительно напряженную плиту армируем стержневой арматурой класса А-VI c электротермическим напряжением на упоры форм.
К трещиностойкости плиты предъявляют требования 3-й категории. Изделие подвергаем тепловой обработке при атмосферном давлении.
Бетон тяжелый класса В40, соответствующий напрягаемой арматуре.
Призменная прочность нормативная ![]() ;
;
расчетная![]() ; коэффициент условий работы бетона
; коэффициент условий работы бетона ![]() ;
;
нормативное сопротивление при растяжении ![]() ; расчетное
; расчетное ![]() ; начальный модуль упругости бетона
; начальный модуль упругости бетона ![]() .
.
Арматура продольных ребер –класса А-VI, нормативное сопротивление
![]() , расчетное сопротивление
, расчетное сопротивление ![]() ,
,
модуль упругости ![]() .
.
Предварительное напряжение арматуры принимаем равным
![]()
Проверяем выполнение условия при электротермическом способе натяжения:
![]()
![]()
![]() условие выполняется.
условие выполняется.
Вычисляем предельное отклонение предварительного напряжения:
D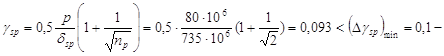 принимаем
принимаем
![]()
где n=2 – число напрягаемых стержней плиты.
Коэффициент точности натяжения при благоприятном влиянии
предварительного напряжения ![]() D
D![]()
При проверке по образованию трещин в верхней зоне плиты при обжатии принимаем: ![]()
Предварительное напряжение с учётом точности натяжения:
![]()
2.1.5 Расчёт прочности плиты по сечению, нормальному к продольной оси
![]()
Сечение тавровое с полкой в сжатой зоне.
Условие:![]() :
:
![]()
Т.к. ![]() , условие выполняется, т.е. нижняя граница сжатой зоны располагается в пределах полки,
, условие выполняется, т.е. нижняя граница сжатой зоны располагается в пределах полки, ![]()
Вычисляем:
![]()
![]()
По таблице 3.1(1) находим: ![]() ;
; ![]() ;
;
![]()
- нейтральная ось проходит в пределах сжатой полки;
Вычисляем граничную высоту сжатой зоны:
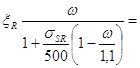
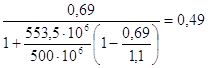
![]()
![]() -при электротермическом способе натяжения;
-при электротермическом способе натяжения;
![]() , т.к.
, т.к. ![]()
![]()
- характеристика деформативных свойств бетона;
Коэффициент условий работы, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести:
![]()
![]() для арматуры класса А-VI; принимаем
для арматуры класса А-VI; принимаем ![]()
Вычисляем площадь сечения растянутой арматуры:
![]()
Принимаем 2Ø14 А-VI с ![]() .
.
2.1.6 Расчёт полки на местный изгиб
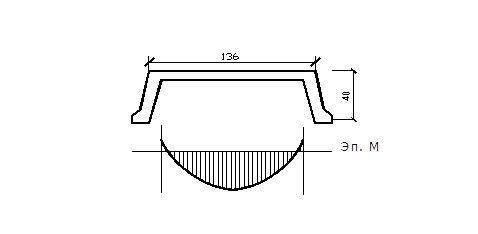
Рисунок 5- К расчету полки плиты на местный изгиб
Расчётный пролёт при ширине рёбер вверху 0,09 м составит
![]() ,
,
Нагрузка на ![]() полки:
полки:
Расчётная нагрузка на ![]() полки составляет:
полки составляет:
![]()
где ![]() - расчётная постоянная нагрузка на плиту от пола,
- расчётная постоянная нагрузка на плиту от пола, ![]()
![]() - расчётная нагрузка от собственного веса полки,
- расчётная нагрузка от собственного веса полки, ![]()
![]()
Изгибающий момент для полосы шириной 1м определяем с учётом частичной заделки в рёбрах ![]()
Рабочая высота сечения ![]()
Арматура Ø4 Вр-I с ![]()
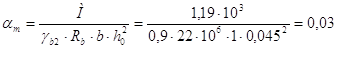
![]()
![]()
![]()
Принимаем 6Ø4Вр-I с ![]() с шагом
с шагом ![]() и нестандартную сварную сетку из одинаковых в обоих направлениях стержней Ø4Вр-I;
и нестандартную сварную сетку из одинаковых в обоих направлениях стержней Ø4Вр-I;
марка сетки:
![]() с
с ![]() .
.
2.2 Расчёт ребристой плиты по предельным состояниям II группы
2.2.1 Геометрические характеристики приведённого сечения
Отношение модулей упругости:
![]()
Площадь приведённого сечения:
![]()
Статический момент площади приведённого сечения относительно нижней грани:
![]()
Расстояние от нижней грани до центра тяжести приведенного сечения:
![]()
Момент инерции приведённого сечения:
![]()
![]()
где ![]() момент инерции
момент инерции ![]() части сечения относительно оси, проходящей через центр тяжести этой части сечения;
части сечения относительно оси, проходящей через центр тяжести этой части сечения;
Момент сопротивления приведённого сечения по нижней зоне
![]()
Момент сопротивления приведённого сечения по верхней зоне
![]()
Расстояние от ядровой точки, наиболее удаленной от растянутой зоны (верхней) до центра тяжести приведённого сечения:
![]()
То же, наименее удаленной от растянутой зоны (нижней):
![]()
Упругопластический момент сопротивления по растянутой зоне:
![]()
где ![]() - коэффициент, принимаемый для тавровых сечений с полкой в сжатой зоне.
- коэффициент, принимаемый для тавровых сечений с полкой в сжатой зоне.
Упругопластический момент по растянутой зоне в стадии изготовления и обжатия элемента:
![]()
где ![]() - коэффициент, принимаемый для таврового сечения с полкой в растянутой зоне при
- коэффициент, принимаемый для таврового сечения с полкой в растянутой зоне при ![]() и
и ![]()
2.2.2Определение потерь предварительного напряжения арматуры
Коэффициент точности натяжения арматуры при этом ![]()
Потери от релаксации напряжений в арматуре при электротермическом способе натяжения канатов:
![]() .
.
Потери от температурного перепада, между натянутой арматурой и упорами ![]() , так как при пропаривании форма с упорами нагревается вместе с изделием.
, так как при пропаривании форма с упорами нагревается вместе с изделием.
Усилие обжатия с учётом полных потерь:
![]()
Эксцентриситет этого усилия относительно центра тяжести приведённого сечения:
![]()
Напряжение в бетоне при обжатии:
![]()
Устанавливаем величину передаточной прочности бетона из условия:
![]()
Принимаем ![]() , тогда
, тогда ![]()
Вычисляем сжимающие напряжения в бетоне на уровне центра тяжести напрягаемой арматуры от усилия обжатия ![]() и с учётом изгибающего момента от массы:
и с учётом изгибающего момента от массы: ![]() , тогда
, тогда
![]()
Потери от быстронатекающей ползучести:
![]() и при
и при ![]()
составляет ![]()
Первые потери:
![]()
С учетом ![]() напряжение
напряжение ![]() равно:
равно:
![]()
![]()
Потери от усадки бетона ![]()
Потери от ползучести бетона при ![]() составляют
составляют
![]()
Вторые потери: ![]()
Полные потери: ![]()
т.е. больше установленного минимального значения потерь.
Усилие обжатия с учётом полных потерь:
![]()
2.2.3 Расчёт прочности плиты по сечению, наклонному к продольной оси
![]()
Влияние продольного усилия обжатия ![]()
![]()
Проверяем, требуется ли поперечная арматура по расчёту.
Условие: ![]() - удовлетворяется. При:
- удовлетворяется. При:
![]()
![]() ,
,
принимаем ![]()
Другое условие:
![]()
![]() - условие удовлетворяется.
- условие удовлетворяется.
Следовательно, поперечная арматура не требуется по расчету.
На приопорных участках длиной ![]() устанавливаем конструктивно в каждом ребре плиты поперечные стержни Ø6 А-I с шагом
устанавливаем конструктивно в каждом ребре плиты поперечные стержни Ø6 А-I с шагом![]() , в средней части пролета шаг
, в средней части пролета шаг ![]() .
.
Поскольку поперечные стержни приняты конструктивно, проверку прочности не производим.
2.2.4 Расчёт по образованию трещин, нормальных к продольной оси
Выполняем для выяснения необходимости проверки по раскрытию трещин. При этом для элементов, к трещиностойкости которых предъявляют требования 3-й категории, принимаем значения коэффициента надежности по нагрузке: ![]()
![]()
![]()
![]()
Условие: ![]()
Вычисляем момент образования трещин по приближённому способу ядровых моментов:
![]()
Здесь ядровый момент усилия обжатия при ![]()
![]()
Поскольку ![]() ,трещины в растянутой зоне образуются.
,трещины в растянутой зоне образуются.
Проверяем, образуются ли начальные трещины в верхней зоне плиты при её обжатии при значении коэффициента точности натяжения ![]() . Изгибающий момент от собственной массы плиты
. Изгибающий момент от собственной массы плиты ![]()
Расчётное условие: ![]()
![]()
![]()
Поскольку ![]() , условие удовлетворяется, начальные трещины не образуются:
, условие удовлетворяется, начальные трещины не образуются:
здесь ![]() - сопротивление бетона растяжению соответствующее передаточной прочности бетона
- сопротивление бетона растяжению соответствующее передаточной прочности бетона ![]() .
.
2.2.5 Расчет по раскрытию трещин, нормальных к продольной оси
Предельная ширина раскрытия трещин: непродолжительная ![]() , продолжительная
, продолжительная ![]() . Изгибающие моменты от нормативных нагрузок: постоянной и длительной
. Изгибающие моменты от нормативных нагрузок: постоянной и длительной ![]() полной
полной ![]()
Приращение напряжений в растянутой арматуре от действия постоянной и длительной нагрузок:
![]()
где ![]() плечо внутренней пары сил;
плечо внутренней пары сил;
![]() так как усилие обжатия Р2 приложено в центре тяжести нижней напрягаемой арматуры;
так как усилие обжатия Р2 приложено в центре тяжести нижней напрягаемой арматуры;
![]() момент сопротивления сечения по растянутой арматуре;
момент сопротивления сечения по растянутой арматуре;
Поскольку приращение напряжений ![]() , трещины в растянутой зоне плиты от действия этого вида нагрузок не образуются и, соответственно, нет прогиба плиты.
, трещины в растянутой зоне плиты от действия этого вида нагрузок не образуются и, соответственно, нет прогиба плиты.
Приращение напряжений в арматуре от действия полной нагрузки:
![]()
Вычисляем:
- ширину раскрытия трещин от непродолжительного действия полной нагрузки:
![]()
где ![]()
![]()
d-диаметр продольной арматуры, м
Непродолжительная ширина раскрытия трещин:
![]()
Продолжительная ширина раскрытия трещин:
![]()
Следовательно, конструкция в целом отвечает требованиям трещиностойкости.
2.2.6 Расчёт плиты на усилия, возникающие в период изготовления, транспортирования и монтажа
Расчет ведем на совместное действие внецентренного сжатия и нагрузки от собственного веса.
За расчётное сечение принимаем сечение, расположенное на расстоянии 1 м от торца панели.
Нагрузка от собственного веса:
![]()
Момент от собственного веса:
![]()
Определяем ![]()
![]() , тогда
, тогда ![]()
![]()
Принимаем арматуру 2Ø22 А-II с ![]() для каркасов КП-1.
для каркасов КП-1.
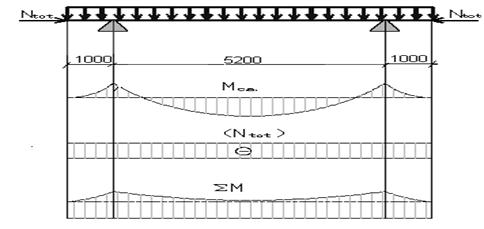
Рисунок 6 - Расчетная схема плиты в период изготовления, транспортирования и монтажа
3. Расчет трехпролетного неразрезного ригеля
Расчетный пролет ригеля между осями колонн ![]() , а в крайних пролетах:
, а в крайних пролетах:
![]()
где ![]() привязка оси стены от внутренней грани, м
привязка оси стены от внутренней грани, м
![]() глубина заделки ригеля в стену, м
глубина заделки ригеля в стену, м
3.1 Материалы ригеля и их расчетные характеристики
Бетон тяжелый класса: В20, ![]()
![]()
![]() , коэффициент
, коэффициент
условий работы бетона ![]() .
.
Арматура:
- продольная рабочая из стали кл.А-III ![]() ; модуль упругости
; модуль упругости ![]()
- поперечная из стали класса А – I, ![]()
3.2 Статический расчет ригеля
Предварительно определяем размеры сечения ригеля:
- высота ![]()
- ширина ![]()
Нагрузка от собственного веса ригеля: ![]()
Нагрузку на ригель собираем с грузовой полосы шириной, равной
номинальной длине плиты перекрытия.
Вычисляем расчетную нагрузку на 1м длины ригеля.
Постоянная:
- от перекрытия с учётом коэффициента надёжности по назначению здания
![]() :
: ![]()
- от массы ригеля с учётом коэффициента надёжности
![]() и
и ![]()
![]()
Итого: ![]()
Временная нагрузка с учётом коэффициента надёжности по назначению здания ![]() :
:
![]()
Полная расчетная нагрузка:
![]()
![]()
Расчетные значения изгибающих моментов и поперечных сил находим в предположении упругой работы неразрезной трехпролетной балки. Схемы загружения и значения M и Q в пролетах и на опорах приведены в табл.2![]()
Таблица 2- Определение изгибающих моментов и поперечных сил
| Схема загружения | M1 | M2 | M3 | MВ | MС | QА | QВ1 | QВ2 |
| 0,08* *26,79**5,552= =66,02 | 0,025* *26,79**5,62= =21 | 66,02 | -0,1* *26,79* *5,62= =-84,01 | -84,01 | 0,4* *26,79* *5,55= =59,47 | -0,6* *26,79* *5,55= =-89,21 | 0,5* *26,79* *5,6= =75,01 |
| 0,101* *52,53* *5,552= =163,42 | -0,05* *52,53* *5,62= =-82,37 | 163,42 | -0,05* *52,53* *5,62= =-82,37 | -82,37 | 0,45* *52,53* *5,55= =131,19 | -0,55* *52,53* *5,55= =-160,35 | 0 |
| -0,025* *52,53* *5,552= =-40,45 | 0,075* *52,53* *5,62= =123,55 | -40,45 | -0,05* *52,53* *5,62= -82,37 | -82,37 | -0,05* *52,53* 5,55= =-14,58 | -0,05* *52,53* *5,55= =-14,58 | 0,5* *52,53* *5,6= =147,08 |
| 117,07 | 82,37 | -21,74 | -0,117* *52,53* *5,62= =-192,74 | -0,033* *52,53* *5,62= =-54,36 | 0,383* *52,53* *5,55= =111,66 | -0,617* *52,53* *5,55= =-179,88 | 0,583* *52,53* *5,6= =171,5 |
| Наиневыгоднейшая комбинация | 1+2 229,44 | 1+3 144,55 | 1+2 229,44 | 1+4 -276,75 | 1+2 -166,38 | 1+2 190,66 | 1+4 -269,09 | 1+4 246,51 |
По данным табл.2 строим эпюры изгибающих моментов и поперечных сил для различных комбинаций нагрузок. При этом значения M и Q от постоянной нагрузки – схема I – входят в каждую комбинацию. Далее производим перерасчет усилий.
Для обеих промежуточных опор устанавливаем одинаковое значение опорного момента, равное сниженному на 30% максимальному значению момента на опоре «В»:
![]() .
.
Исходя из принятого опорного момента, отдельно для каждой комбинации осуществляем перераспределение моментов между опорными и промежуточными сечениями добавлением треугольных эпюр моментов.
Опорный момент ригеля по грани колонны на опоре «В» со стороны второго пролета при высоте сечения колонны ![]()
![]()
Для расчета прочности по сечениям, наклонным к продольной оси, принимаем значения поперечных сил ригеля, большие из двух расчетов: упругого расчета и с учетом перераспределения моментов.
3.3 Расчёт прочности ригеля по сечениям, нормальным к продольной оси
Высоту сечения ригеля уточняем по опорному моменту по грани колонны при ![]() , поскольку на опоре момент определен с учетом образования пластического шарнира. Принятую высоту затем проверяем по пролетному наибольшему моменту так, чтобы относительная высота сжатой зоны была
, поскольку на опоре момент определен с учетом образования пластического шарнира. Принятую высоту затем проверяем по пролетному наибольшему моменту так, чтобы относительная высота сжатой зоны была ![]() и исключалось неэкономичное переармирование сечения. По табл. III.1.(1) при
и исключалось неэкономичное переармирование сечения. По табл. III.1.(1) при ![]() находим значение
находим значение ![]() , а по формуле определяем граничную высоту сжатой зоны:
, а по формуле определяем граничную высоту сжатой зоны:
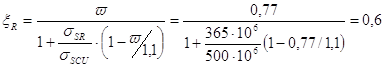
![]()
характеристика деформативных свойств бетона.
![]() , т.к.
, т.к. ![]()
Определяем рабочую высоту сечения ригеля:
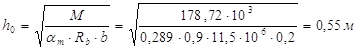
Полная высота сечения:
![]()
С учетом унификации принимаем ![]() ,
, ![]()
Для опорных и пролётных сечений принято расстояние от границы растянутой грани до центра тяжести растянутой арматуры а=0,06 м при расположении арматуры в 2 ряда и а =0,03 м при расположении арматуры в 1 ряд.
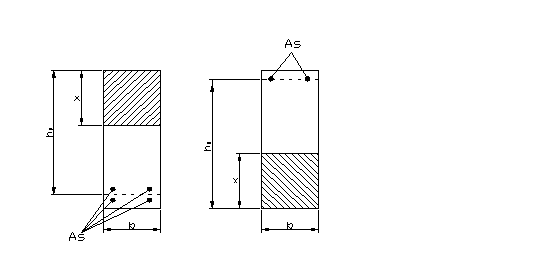 Рисунок 8- К расчету прочности ригеля – сечение
Рисунок 8- К расчету прочности ригеля – сечение
- в пролете (а) - на опоре (б)
Сечение в первом пролёте: ![]() ,
, ![]()
Расчет сечения арматуры выполняем, используя вспомогательные таблицы, вычисляем
![]()
По табл.![]() находим
находим ![]() ,
, ![]()
Проверяем принятую высоту сечения ригеля. Поскольку ![]() , сечение не будет переармированным.
, сечение не будет переармированным.
Определяем площадь сечения продольной арматуры:
![]()
По сортаменту принимаем для армирования 2Ø18А-III+ 2Ø20А-III с
![]() .
.
Сечение в среднем пролёте ![]()
![]()
![]()
![]()
По сортаменту принимаем ![]() 4Ø14А-III c
4Ø14А-III c![]()
Количество верхней арматуры определяем по величине опорных изгибающих моментов.
Сечение на опоре «В», ![]()
![]()
![]()
![]()
Для армирования опорных сечений принимаем:
- со стороны 1го пролета 2Ø10А-III +2Ø22A-III c ![]()
- со стороны 2го пролета : сечение арматуры, доводимой до опор, определяем исходя из значения отрицательного момента, ![]() ,
, ![]()
Вычисляем:
![]()
![]()
Сечение арматуры:
![]()
Следовательно, до опор должна доводиться арматура не менее 2Ø 16 А-III с ![]()
Принимаем 2Ø16 А-III +2Ø18A-III c ![]() .
.
3.4 Расчёт прочности ригеля по сечениям, наклонным к продольной оси
Максимальная поперечная сила (на первой промежуточной опоре слева) ![]()
Диаметр поперечных стержней устанавливаем из условия сварки с продольной арматурой диаметром d=22 мм и принимаем равным d=8 мм класса А-I с ![]() .Шаг поперечных стержней по конструктивным условиям принимаем s=h/3=0,6/3=0,2м. На всех приопорных участках длиной 0,25L принимаем шаг s=0,2м; в средней части пролета шаг s=(3/4)h=0,75х0,6=0,45м.
.Шаг поперечных стержней по конструктивным условиям принимаем s=h/3=0,6/3=0,2м. На всех приопорных участках длиной 0,25L принимаем шаг s=0,2м; в средней части пролета шаг s=(3/4)h=0,75х0,6=0,45м.
Вычисляем:
![]()
![]()
![]()
Условие ![]() выполняется.
выполняется.
Требование ![]() - выполняется.
- выполняется.
При расчете прочности вычисляем:
![]()
Поскольку
![]() ,
,
вычисляем значение (с) по формуле:
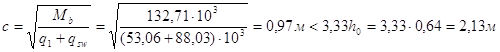
Тогда ![]()
Поперечная сила в вершине наклонного сечения
![]() .
.
Длина проекции расчетного наклонного сечения
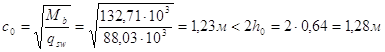
Вычисляем ![]()
Условие
![]() удовлетворяется.
удовлетворяется.
Проверка прочности по сжатой наклонной полосе:
![]()
![]()
![]()
![]()
Условие прочности:
![]()
удовлетворяется.
3.5 Построение эпюры арматуры
Эпюру арматуры строим в такой последовательности:
- определяем изгибающие моменты М, воспринимаемые в расчетных сечениях, по фактически принятой арматуре;
- устанавливаем графически или аналитически на огибающей эпюре моментов по ординатам М места теоретического обрыва стержней;
- определяем длину анкеровки обрываемых стержней
![]() , причем поперечная сила Q в месте теоретического обрыва стержня принимаем соответствующей изгибающему моменту в этом сечении; здесь d – диаметр обрываемого стержня.
, причем поперечная сила Q в месте теоретического обрыва стержня принимаем соответствующей изгибающему моменту в этом сечении; здесь d – диаметр обрываемого стержня.
- в пролете допускается обрывать не более 50% расчетной площади сечения стержней, вычисленных по максимальному изгибающему моменту.
Рассмотрим сечение первого пролёта. Арматура 2Ø18А-III+ 2Ø20А-III c ![]()
Определяем момент, воспринимаемый сечением, для чего рассчитываем необходимые параметры:
![]()
![]()
![]() ,
, ![]()
![]()
Арматура 2Ø18A-III обрывается в пролете, а стержни 2Ø20 А-III c ![]() доводятся до опор.
доводятся до опор.
Определяем момент, воспринимаемый сечением с этой арматурой:
![]()
![]()
![]() ,
, ![]()
![]()
Графически определяем точки обрыва двух стержней 2Ø18А-III . В первом сечении поперечная сила ![]() , во втором
, во втором ![]() . Интенсивность поперечного армирования в первом сечении при шаге хомутов
. Интенсивность поперечного армирования в первом сечении при шаге хомутов ![]() равна:
равна:
![]()
Длина анкеровки
![]()
Во втором сечении при шаге хомутов ![]()
![]()
![]()
Сечение во втором пролете: принята арматура 4Ø14А-III c![]() .
.
Определяем момент, воспринимаемый сечением, для чего рассчитываем необходимые параметры:
![]()
![]()
![]() ,
, ![]()
![]()
Арматура 2Ø14A-III обрывается в пролете, а стержни 2Ø14А-III c ![]() доводятся до опор. Определяем момент, воспринимаемый сечением с этой арматурой :
доводятся до опор. Определяем момент, воспринимаемый сечением с этой арматурой :
![]()
![]()
![]() ,
, ![]()
![]()
Графически определяем точки обрыва двух стержней Ø14 A-III. Поперечная сила в сечении ![]() . Интенсивность поперечного армирования при шаге хомутов
. Интенсивность поперечного армирования при шаге хомутов ![]() равна:
равна:
![]()
Длина анкеровки
![]()
На первой промежуточной опоре слева принята арматура 2Ø10А-III+
+2Ø22A-III c ![]() .
.
![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]()
Стержни 2Ø10А-III c ![]() доводятся до опор.
доводятся до опор.
Определяем момент, воспринимаемый сечением с этой арматурой:
![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]() .
.
Поперечная сила ![]() . Интенсивность поперечного армирования при шаге хомутов
. Интенсивность поперечного армирования при шаге хомутов ![]() равна:
равна:
![]()
![]() . Принимаем
. Принимаем ![]() .
.
На первой промежуточной опоре справа принята арматура 2Ø16А-III+ +2Ø18A-III c ![]() .Определяем момент, воспринимаемый сечением c этой арматурой:
.Определяем момент, воспринимаемый сечением c этой арматурой:
![]() ,
, ![]() ,
,
![]()
![]()
![]()
Стержни 2Ø16А-III с ![]() доводятся до опор:
доводятся до опор:
![]() ,
,![]()
![]()
![]()
![]()
Поперечная сила ![]() . Интенсивность поперечного армирования при шаге хомутов
. Интенсивность поперечного армирования при шаге хомутов ![]() :
: ![]()
Длина анкеровки
![]()
Принимаем ![]() .
.
3.6 Расчет стыка ригеля с колонной
Рассматриваем вариант бетонированного стыка. В этом случае изгибающий момент на опоре воспринимается соединительными стержнями в верхней растянутой зоне и бетоном, заполняющим полость между торцом ригелей и колонной.
Принимаем бетон для замоноличивания класса В20, ![]()
![]() стыковые стержни из арматуры класса A-III;
стыковые стержни из арматуры класса A-III; ![]()
Изгибающий момент ригеля на грани колонны ![]() , рабочая высота сечения
, рабочая высота сечения ![]()
![]()
по табл.III.I.(1) находим соответствующее значение ![]() и определяем площадь сечения стыковых стержней
и определяем площадь сечения стыковых стержней
![]()
Принимаем арм