Автоматизация измерений, контроля и испытаний

1. Основы метрологического обеспечения

Под метрологическим обеспечением (МО) понимается установление и применение научных и организационных основ, технических средств, правил и норм, необходимых для достижения единства и требуемой точности измерении. Основной тенденцией в развитии МО является переход от существовавшей ранее сравнительно узкой задачи обеспечения единства и требуемой точности измерений к принципиально новой задаче обеспечения качества измерений.

Качество измерений понятие более широкое, чем точность измерений. Оно характеризует совокупность свойств СИ, обеспечивающих получение в установленный срок результатов измерений с требуемыми точностью (размером допускаемых погрешностей), достоверностью, правильностью, сходимостью и воспроизводимостью.

Понятие "метрологическое обеспечение" применяется, как правило, по отношению к измерениям (испытанию, контролю) в целом. В то же время допускают использование термина "метрологическое обеспечение технологического процесса (производства, организации)", подразумевая при этом МО измерений (испытаний или контроля) в данном процессе, производстве, организации. Объектом МО являются все стадии жизненного цикла (ЖЦ) изделия (продукции) или услуги. Под ЖЦ понимается совокупность последовательных взаимосвязанных процессов создания и изменения состояния продукции от формулирования исходных требований к ней до окончания эксплуатации или потребления.

Так, на стадии разработки продукции для достижения высокого качества изделия производится выбор контролируемых параметров, норм точности, допусков, средств измерения, контроля и испытания. Так же осуществляется метрологическая экспертиза конструкторской и технологической документации. При разработке МО необходимо использовать системный подход, суть которого состоит в рассмотрении указанного обеспечения как совокупности взаимосвязанных процессов, объединенных одной целью достижением требуемого качества измерений. Такими процессами являются:

• установление рациональной номенклатуры измеряемых параметров и оптимальных норм точности измерений при контроле качества продукции и управлении процессами;

• технико-экономическое обоснование и выбор СИ, испытаний и контроля и установление их рациональной номенклатуры;

• стандартизация, унификация и агрегатирование используемой контрольно-измерительной техники;

• разработка, внедрение и аттестация современных методик выполнения измерения, испытаний и контроля (МВИ);

• поверка, метрологическая аттестация и калибровка контрольно-измерительного и испытательного оборудования (КИО), применяемого на предприятии;

• контроль за производством, состоянием, применением и ремонтом КИО, а также за соблюдением метрологических правил и норм на предприятии;

• участие в разработке и внедрении стандартов предприятия;

• внедрение международных, государственных и отраслевых стандартов, а также иных нормативных документов Госстандарта;

• проведение метрологической экспертизы проектов нормативной, конструкторской и технологической документации;

• проведение анализа состояния измерений, разработка на его основе и осуществление мероприятий по совершенствованию МО;

• подготовка работников соответствующих служб и подразделений предприятия к выполнению контрольно-измерительных операций.

Метрологическое обеспечение имеет четыре основы: научную, организационную, нормативную и техническую. Отдельные аспекты МО рассмотрены в рекомендации МИ 2500-98 по метрологическому обеспечению малых предприятий. Разработка и проведение мероприятий МО возложено на метрологические службы (МС). Метрологическая служба служба, создаваемая в соответствии с законодательством для выполнения работ по обеспечению единства измерений и осуществления метрологического контроля и надзора.

2. Цифровые устройства: шифраторы и дешифраторы, сумматоры, счетчики, мультиплексоры, регистры, магнитоэлектронные переключатели

Интегральные счетчики

Интегральный счетчик — цифровое устройство (цифровая микросхема или ее часть), выполненное на интегральных триггерах со схемами управления разной структуры и осуществляющее счет поступающих на его вход импульсов. Счет импульсов в счетчик представляется определенными комбинациями состояний триггеров. При поступлении на вход схемы очередной логической 1 в счетчике устанавливается новая комбинация состояний триггеров, соответствующая числу, превышающему предыдущее на единицу. Такие счетчики называют суммирующими. В цифровой измерительной технике применяют и вычитающие счетчики, в которых в процессе счета входные числа последовательно убывают на единицу, а также реверсивные счетчики, способные переключаться из режима суммирования в режим вычитания и наоборот.

Для представления чисел в счетчиках используются в основном двоичная, десятичная и двоично-десятичная системы счислений. При применении двоичной системы счисления логические уровни на прямых выходах триггеров определяют цифры двоичных разрядов числа. В этом случае каждый разряд числа в счетчике обеспечивается определенным состоянием одного триггера. Максимальное число импульсов, которое может быть записано, составляет N = 2^л-1, где п — число разрядов (число триггеров) в счетчике.

Рассмотрим простейший двоичный кольцевой счетчик, представляющий собой три замкнутых в кольцо JК-триггеров (рис.1, а), по которым под воздействием входных импульсов (точка Вх) циркулирует одна пли несколько кодовых единиц.

В рассматриваемой схеме прямой выход каждого предыдущего триггера соединен с входом J последующего триггера. Тактовые входы С всех триггеров объединены (узел Вх.) и на них поступают счетные импульсы. Перед началом счета первый триггер импульсным сигналом Уст. устанавливается в состояние 1, остальные триггеры — в состояние 0. Этому состоянию счетчика соответствует 0 на выходе Q ₃ последнего триггера. После отключения сигнала Уст, начинается счет, и триггеры функционируют как обычные JK-триггеры.

Поскольку на информационных входах первого триггера было установлено J = 0 и К = 1, в момент окончания первого входного импульса он перейдет в состояние логического 0. Второй триггер примет состояние 1, так как на его входах было J = К = 1. Третий триггер не изменит своего предыдущего состояния. Таким образом, кодовая 1 перешла с первого триггера на второй. По окончании каждого следующего входного импульса 1 будет перемещаться от предыдущего триггера к последующему, т.е. переходить по схеме вправо (см. таблицу истинности на рис. 1, б).

рис.1. Кольцевой счетчик:

а – схема; б – таблица истинности

Шифраторы и дешифраторы

Прежде чем перейти к рассмотрению специфических устройств цифровой измерительной техники- шифраторов и дешифраторов, обратимся к системам отображения цифровой информации.

Системы счисления и коды, применяемые в цифровой измерительной технике. Для изображения любых чисел существует некоторое ограниченное число знаков и порядок их написания — это и есть система счисления. В наиболее привычной для нас десятичной системе таких знаков десять: 0, 1, 2,..., 9. Форма записи числа в десятичной систем счисления имеет вид:

(1)

где 10 ⁱ — десятичный разряд; а_i — значение символа в соответствующем разряде, которое может быть любым от 0 до 9.

Например, число 583 с помощью трех десятичных разрядов запишется как: N = 583 = 10²-5 + 10'-8 + 10°-3.

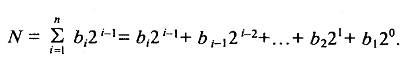Аналогично записывается целое число и в двоичной системе счисления:

Здесь коэффициенты b _i, принимают лишь два значения: 0 и 1. Например, число 583 в двоичной системе запишется в виде

N= 1^.2⁹+0^.2⁸ + 0.2⁷ + 1^. 2⁶+0.2⁵+0^.2⁴+0.2³+ 1. 2² + 1^.2'+ 1^.2°. (3)

Следовательно, числу 583 в десятичной системе соответствует число в двоичной - 1001000111. Последнее принято называть кодом числа в двоичной системе счисления. Написание числа в двоичном коде оказывается удобным для проведения арифметических действий по законам булевой алгебры, что применяется в вычислительных устройствах и, в частности, в компьютерах.

При использовании десятичной системы счисления для образования кода требуется десять различных импульсов, например отличающихся амплитудой, длительностью и пр. Такое представление кодов не применяют, так как для образования и его распознавания требуется сложная аппаратура, в то время как для образования и обработки двоичного кода могут быть использованы простые, двоичные элементы, имеющие всего два состояния: единица и нуль. Двоичный код наиболее компактен (экономичен) и пока является основным кодом в компьютерной технике. Однако двоичный код неудобен для управления десятичным цифровым отсчетным устройством измерительной аппаратуры.

Поэтому в цифровой измерительной аппаратуре широко используется двоично-десятичные и тетрадно-десятичные коды, так как представление измеряемой величины на индикаторе должно быть выполнено в привычном для наблюдающего человека десятичном виде, а перевод двоичного кода в десятичный — сложная задача для оператора.

В тетрадно-десятичной системе каждая десятичная цифра (0...9) кодируется четырьмя двоичными числами 0 и 1 (тетрада) при различных носовых коэффициентах. Широко распространен в цифровых измерительных приборах (ЦИП) код 8421, в котором весовыми коэффициентами являются цифры 8, 4, 2, 1 (табл.1).

Таблица 1. Двоично-десятичный код 8421

Десятичные цифры	0	1	2	3	4	5	6	7	8	9
Код 8421	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001

Если вернуться к числу 583, то в коде 8421 оно будет представлено следующим образом:

583=10²(8-0+41+2-0+1-1)+10'(8-1+4-0+20+1-0)+10°(8-0+4-0+21 + 11). (4)

Соответственно тетрадно-десятичная запись имеет вид

0101 1000 0011

Помимо двоично-десятичного кода при построении цифровых измерительных приборов применяются коды и с другими весовыми коэффициентами (тетрадно-десятичные коды), например: 4 2 2 1 и др. Эти коды неоднозначные (т.е. числа можно получить разными комбинациями), но требуют меньше символов, что иногда важно. Для устранения неоднозначности принимают специальные меры.

В широко используемых в цифровой измерительной технике десятичных (декадных) счетчиках цифры разрядов десятичного числа представляются в четырехразрядной двоичной форме, т.е. используется двоично-десятичная система исчисления. При этом для каждого разряда десятичного числа используется четыре триггера и, если число десятичных разрядов к, то для регистрации чисел в десятичном счетчике необходимо задействовать 4к триггеров. Максимальное число записанных импульсов в счетчике в этом случае составляет N = 10^k- 1. Десятичные счетчики широко применяют в случаях, когда число поступающих импульсов необходимо представить в привычной для человека десятичной системе счисления.

Шифратор(называемый часто кодером) — устройство, преобразующее десятичные числа в двоичную систему счисления. Пусть в шифраторе имеется т входов, последовательно пронумерованных десятичными числами (0, 1, 2, 3,..., т - 1), и п выходов. Поступление сигнала на один из входов вызывает появление на выходах n-разрядного двоичного числа, соответствующего номеру возбужденного входа.

Из теории передачи информации известно, что построить шифраторы с большим числом входов т технически трудно, поэтому они используются для преобразования в двоичную систему счисления небольших десятичныхчисел. Для преобразования больших десятичных чисел используются специальные методы.

Шифраторы часто снабжаются клавиатурой, каждая клавиша которой связана с определенным входом шифратора, и на его выходе воспроизводится двоичное число, соответствующее написанному на клавише символу.

На рис.2 показано условное изображение шифратора, преобразующего первые десять цифр десятичного счисления 0, 1, 2,..., 9 в двоичное представление. Символ CD в обозначении образован из букв, входящих в английское слово CODER, Слева на схеме показано десять входов, обозначенных соответствующими десятичными числами. Справа представлены выходы шифратора: цифрами 1, 2, 4, 8 обозначены весовые коэффициенты двоичных разрядов, соответствующих отдельным выходам.

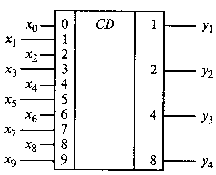Рис.2. Условное изображение шифратора

Дешифратор(называемый также декодером) предназначен для обратного преобразования двоичных чисел в сравнительно небольшие по значению десятичные числа. Входы дешифратора служат для подачи двоичных чисел, выходы последовательно нумеруются десятичными числами. Дешифраторы широко используются в цифровой измерительной технике. В частности, их применяют в устройствах, печатающих на бумаге выводимые из цифровой схемы текст или числа. В таких устройствах двоичное число, поступая на соответствующий вход дешифратора, вызывает появление сигнала на его определенном выходе.

На рис. 3. в качестве примера приведено условное изображение одной из простейших структурных схем дешифратора. Символ DC образован из букв английского слова DECODER.

Слева от схемы представлены входы шифратора: цифрами 1, 2, 4, 8 обозначены весовые коэффициенты дешифратора двоичных разрядов. Справа показаны десять выходов, пронумерованных десятичными числами, соответствующими отдельным комбинациям входного двоичного числа. На каждом выходе дешифратора при строго определенной комбинации входного двоичного кода вырабатывается логическая 1.

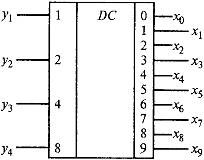
Рис.3. Условное изображение дешифратора

Сумматоры.

Основной элементарной операцией, выполняемой над кодами чисел в цифровых устройствах, является арифметическое сложение.

Сумматор — логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учёт знаков чисел, выравнивание порядков слагаемых и тому подобное. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры.

Сумматоры классифицируют по различным признакам.

В зависимости от системы счисления различают:

· двоичные;

· двоично-десятичные (в общем случае двоично-кодированные);

· десятичные;

· прочие (например, амплитудные).

По количеству одновременно обрабатываемых разрядов складываемых чисел:

· одноразрядные,

· многоразрядные.

По числу входов и выходов одноразрядных двоичных сумматоров:

· четвертьсумматоры (элементы “сумма по модулю 2”; элементы “исключающее ИЛИ”), характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма;

· полусумматоры, характеризующиеся наличием двух входов, на которые подаются одноимённые разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма в данном разряде, а на другом — перенос в следующий (более старший разряд);

· полные одноразрядные двоичные сумматоры, характеризующиеся наличием трёх входов, на которые подаются одноимённые разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма в данном разряде, а на другом — перенос в следующий (более старший разряд).

По способу представления и обработки складываемых чисел многоразрядные сумматоры подразделяются на:

· последовательные, в которых обработка чисел ведётся поочерёдно, разряд за разрядом на одном и том же оборудовании;

· параллельные, в которых слагаемые складываются одновременно по всем разрядам, и для каждого разряда имеется своё оборудование.

Параллельный сумматор в простейшем случае представляет собой n одноразрядных сумматоров, последовательно (от младших разрядов к старшим) соединённых цепями переноса. Однако такая схема сумматора характеризуется сравнительно невысоким быстродействием, так как формирование сигналов суммы и переноса в каждом i-ом разряде производится лишь после того, как поступит сигнал переноса с (i-1)-го разряда. Таким образом, быстродействие сумматора определяется временем распространения сигнала по цепи переноса. Уменьшение этого времени — основная задача при построении параллельных сумматоров.

Для уменьшения времени распространения сигнала переноса применяют: конструктивные решения, когда используют в цепи переноса наиболее быстродействующие элементы; тщательно выполняют монтаж без длинных проводников и паразитных ёмкостных составляющих нагрузки и (наиболее часто) структурные методы ускорения прохождения сигнала переноса.

По способу организации межразрядных переносов параллельные сумматоры, реализующие структурные методы, делят на сумматоры:

· с последовательным переносом;

· с параллельным переносом;

· с групповой структурой;

· со специальной организацией цепей переноса.

Среди сумматоров со специальной организацией цепей переноса можно указать:

· сумматоры со сквозным переносом, в которых между входом и выходом переноса одноразрядного сумматора оказывается наименьшее число логических уровней;

· сумматоры с двухпроводной передачей сигналов переноса;

· сумматоры с условным переносом (вариант сумматора с групповой структурой, позволяющий уменьшить время суммирования в 2 раза при увеличении оборудования в 1,5 раза);

· асинхронные сумматоры, вырабатывающие признак завершения операции суммирования, при этом среднее время суммирования уменьшается, поскольку оно существенно меньше максимального.

Сумматоры, которые имеют постоянное время, отводимое для суммирования, независимое от значений слагаемых, называют синхронными.

По способу выполнения операции сложения и возможности сохранения результата сложения можно выделить три основных вида сумматоров:

· комбинационный, выполняющий микрооперацию “S = A плюс B”, в котором результат выдаётся по мере его образования (это комбинационная схема в общепринятом смысле слова);

· сумматор с сохранением результата “S = A плюс B”;

· накапливающий, выполняющий микрооперацию “S = S плюс B”.

Последние две структуры строятся либо на счётных триггерах (сейчас практически не используются), либо по структуре “комбинационный сумматор – регистр хранения” (сейчас наиболее употребляемая схема).

Важнейшими параметрами сумматоров являются:

· разрядность;

· статические параметры: Uвх, Uвх, Iвх и так далее, то есть обычные параметры интегральных схем;

· динамические параметры. Сумматоры характеризуются четырьмя задержками распространения:

· от подачи входного переноса до установления всех выходов суммы при постоянном уровне на всех входах слагаемых;

· от одновременной подачи всех слагаемых до установления всех выходов суммы при постоянном уровне на входе переноса;

· от подачи входного переноса до установления выходного переноса при постоянном уровне на входах слагаемых;

· от подачи всех слагаемых до установления выходного переноса при постоянном уровне на входах слагаемых.

Четвертьсумматор

Простейшим двоичным суммирующим элементом является четвертьсумматор. Происхождение названия этого элемента следует из того, что он имеет в два раза меньше выходов и в два раза меньше строк в таблице истинности по сравнению с полным двоичным одноразрядным сумматором. Наиболее известны для данной схемы названия: элемент “сумма по модулю 2” и элемент “исключающее ИЛИ”. Схема (рис. 4) имеет два входа а и b для двух слагаемых и один выход S для суммы. Работу её отражает таблица истинности 1 (табл. 2), а соответствующее уравнение имеет вид