Высшая математика
Основные теоремы и определения
Определение. Сумма членов бесконечной числовой последовательности ![]() называется числовым рядом.
называется числовым рядом.
![]()
При этом числа ![]() будем называть членами ряда, а un – общим членом ряда.
будем называть членами ряда, а un – общим членом ряда.
Определение. Суммы ![]() , n = 1, 2, … называются частными (частичными) суммами ряда.
, n = 1, 2, … называются частными (частичными) суммами ряда.
Таким образом, возможно рассматривать последовательности частичных сумм ряда S1, S2, …,Sn, …
Определение. Ряд ![]() называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.
называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.
![]()
Определение. Если последовательность частных сумм ряда расходится, т.е. не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся и ему не ставят в соответствие никакой суммы.
Свойства рядов.
1) Сходимость или расходимость ряда не нарушится если изменить, отбросить или добавить конечное число членов ряда.
2) Рассмотрим два ряда ![]() и
и ![]() , где С – постоянное число.
, где С – постоянное число.
Теорема. Если ряд ![]() сходится и его сумма равна S, то ряд
сходится и его сумма равна S, то ряд ![]() тоже сходится, и его сумма равна СS. (C ¹ 0)
тоже сходится, и его сумма равна СS. (C ¹ 0)
3) Рассмотрим два ряда ![]() и
и ![]() . Суммой или разностью этих рядов будет называться ряд
. Суммой или разностью этих рядов будет называться ряд ![]() , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
Теорема. Если ряды ![]() и
и ![]() сходятся и их суммы равны соответственно S и s, то ряд
сходятся и их суммы равны соответственно S и s, то ряд ![]() тоже сходится и его сумма равна S + s.
тоже сходится и его сумма равна S + s.
![]()
Разность двух сходящихся рядов также будет сходящимся рядом.
Сумма сходящегося и расходящегося рядов будет расходящимся рядом.
О сумме двух расходящихся рядов общего утверждения сделать нельзя.
При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
Критерий Коши.
(необходимые и достаточные условия сходимости ряда)
Для того, чтобы последовательность ![]() была сходящейся, необходимо и достаточно, чтобы для любого
была сходящейся, необходимо и достаточно, чтобы для любого ![]() существовал такой номер N, что при n > N и любом p > 0, где р – целое число, выполнялось бы неравенство:
существовал такой номер N, что при n > N и любом p > 0, где р – целое число, выполнялось бы неравенство:
![]() .
.
1.3 Определение. Ряд ![]() называется равномерно сходящимся на отрезке (a,b), если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
называется равномерно сходящимся на отрезке (a,b), если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
Теорема. (Критерий Коши равномерной сходимости ряда)
Для равномерной сходимости ряда ![]() необходимо и достаточно, чтобы для любого числа e>0 существовал такой номер N(e), что при n>N и любом целом p>0 неравенство
необходимо и достаточно, чтобы для любого числа e>0 существовал такой номер N(e), что при n>N и любом целом p>0 неравенство
![]()
выполнялось бы для всех х на отрезке (a,b).
Теорема. (Признак равномерной сходимости Вейерштрасса)
(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)
Ряд ![]() сходится равномерно и притом абсолютно на отрезке (a,b), если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :
сходится равномерно и притом абсолютно на отрезке (a,b), если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :
![]()
т.е. имеет место неравенство:
![]() .
.
Еще говорят, что в этом случае функциональный ряд ![]() мажорируется числовым рядом
мажорируется числовым рядом ![]() .
.
ряд ![]() называется положительным, если Un≥0, для всех n € N
называется положительным, если Un≥0, для всех n € N
Интегральный признак Коши.
Если j(х) – непрерывная положительная функция, убывающая на промежутке (1;¥), то ряд j(1) + j(2) + …+ j(n) + … = ![]() и несобственный интеграл
и несобственный интеграл ![]() одинаковы в смысле сходимости.
одинаковы в смысле сходимости.
Пример. Ряд ![]() сходится при a>1 и расходится a£1 т.к. соответствующий несобственный интеграл
сходится при a>1 и расходится a£1 т.к. соответствующий несобственный интеграл ![]() сходится при a>1 и расходится a£1. Ряд
сходится при a>1 и расходится a£1. Ряд ![]() называется общегармоническим рядом.
называется общегармоническим рядом.
Следствие. Если f(x) и j(х) – непрерывные функции на интервале (a, b) и ![]() то интегралы
то интегралы 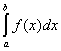 и
и 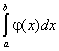 ведут себя одинаково в смысле сходимости.
ведут себя одинаково в смысле сходимости.
Степенные ряды.
Определение. Степенным рядом называется ряд вида
![]() .
.
Для исследования на сходимость степенных рядов удобно использовать признак Даламбера.
Пример. Исследовать на сходимость ряд ![]()
Применяем признак Даламбера:
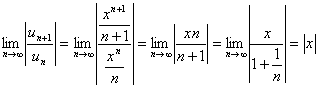 .
.
Получаем, что этот ряд сходится при ![]() и расходится при
и расходится при ![]() .
.
Теперь определим сходимость в граничных точках 1 и –1.
При х = 1: ![]() ряд сходится по признаку Лейбница (см. Признак Лейбница. ).
ряд сходится по признаку Лейбница (см. Признак Лейбница. ).
При х = -1: ![]() ряд расходится (гармонический ряд).
ряд расходится (гармонический ряд).
1 теорема Абеля.
(Нильс Хенрик Абель (1802 – 1829) – норвежский математик)
Теорема. Если степенной ряд ![]() сходится при x = x1 , то он сходится и притом абсолютно для всех
сходится при x = x1 , то он сходится и притом абсолютно для всех ![]() .
.
Доказательство. По условию теоремы, так как члены ряда ограничены, то
![]()
где k- некоторое постоянное число. Справедливо следующее неравенство:
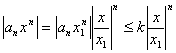
Из этого неравенства видно, что при x
Поэтому на основании признака сравнения делаем вывод, что ряд ![]() сходится, а значит ряд
сходится, а значит ряд ![]() сходится абсолютно.
сходится абсолютно.
Таким образом, если степенной ряд ![]() сходится в точке х1, то он абсолютно сходится в любой точке интервала длины 2
сходится в точке х1, то он абсолютно сходится в любой точке интервала длины 2![]() с центром в точке х = 0.
с центром в точке х = 0.
Следствие. Если при х = х1 ряд расходится, то он расходится для всех ![]() .
.
Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что ![]() ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех ![]() ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.
ряд расходится. При этом число R называется радиусом сходимости. Интервал (-R, R) называется интервалом сходимости.
Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым.
Радиус сходимости может быть найден по формуле:
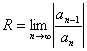
Определение. Тригонометрическим рядом называется ряд вида:
![]()
или, короче, ![]()
Действительные числа ai, bi называются коэффициентами тригонометрического ряда.
Определение. Тригонометрическим рядом называется ряд вида:
![]()
или, короче, ![]()
3,3
2 Теорема Абеля. Если степенной ряд ![]() сходится для положительного значения х=х1 , то он сходится равномерно в любом промежутке внутри
сходится для положительного значения х=х1 , то он сходится равномерно в любом промежутке внутри ![]() .
.
Признак сравнения рядов с неотрицательными членами.
Пусть даны два ряда ![]() и
и ![]() при un, vn ³ 0.
при un, vn ³ 0.
Теорема. Если un £ vn при любом n, то из сходимости ряда ![]() следует сходимость ряда
следует сходимость ряда ![]() , а из расходимости ряда
, а из расходимости ряда ![]() следует расходимость ряда
следует расходимость ряда ![]() .
.
Доказательство. Обозначим через Sn и sn частные суммы рядов ![]() и
и ![]() . Т.к. по условию теоремы ряд
. Т.к. по условию теоремы ряд ![]() сходится, то его частные суммы ограничены, т.е. при всех n sn < M, где М – некоторое число. Но т.к. un £ vn, то Sn £ sn то частные суммы ряда
сходится, то его частные суммы ограничены, т.е. при всех n sn < M, где М – некоторое число. Но т.к. un £ vn, то Sn £ sn то частные суммы ряда ![]() тоже ограничены, а этого достаточно для сходимости.
тоже ограничены, а этого достаточно для сходимости.
Пример. Исследовать на сходимость ряд ![]()
Т.к. ![]() , а гармонический ряд
, а гармонический ряд ![]() расходится, то расходится и ряд
расходится, то расходится и ряд ![]() .
.
Пример. Исследовать на сходимость ряд ![]()
Т.к. ![]() , а ряд
, а ряд ![]() сходится ( как убывающая геометрическая прогрессия), то ряд
сходится ( как убывающая геометрическая прогрессия), то ряд ![]() тоже сходится.
тоже сходится.
Также используется следующий признак сходимости:
Теорема. Если ![]() и существует предел
и существует предел ![]() , где h – число, отличное от нуля, то ряды
, где h – число, отличное от нуля, то ряды ![]() и
и ![]() ведут одинаково в смысле сходимости.
ведут одинаково в смысле сходимости.
Разложение функций в степенной ряд имеет большое значение для решения различных задач исследования функций, дифференцирования, интегрирования, решения дифференциальных уравнений, вычисления пределов, вычисления приближенных значений функции.
Возможны различные способы разложения функции в степенной ряд. Такие способы как разложение при помощи рядов Тейлора и Маклорена были рассмотрены ранее. (См. Формула Тейлора. )
Существует также способ разложения в степенной ряд при помощи алгебраического деления. Это – самый простой способ разложения, однако, пригоден он только для разложения в ряд алгебраических дробей
Рассмотрим способ разложения функции в ряд при помощи интегрирования.
С помощью интегрирования можно разлагать в ряд такую функцию, для которой известно или может быть легко найдено разложение в ряд ее производной.
Находим дифференциал функции ![]() и интегрируем его в пределах от 0 до х.
и интегрируем его в пределах от 0 до х.
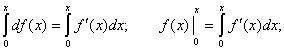
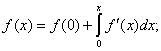
2) Теорема о почленном интегрировании ряда.
Равномерно сходящийся на отрезке (a,b) ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку (a,b) , сходится к интегралу от суммы ряда по этому отрезку.
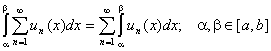
3) Теорема о почленном дифференцировании ряда.
Если члены ряда ![]() сходящегося на отрезке (a,b) представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных
сходящегося на отрезке (a,b) представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных ![]() сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
![]()
На основе того, что сумма ряда является некоторой функцией от переменной х, можно производить операцию представления какой – либо функции в виде ряда (разложения функции в ряд), что имеет широкое применение при интегрировании, дифференцировании и других действиях с функциями.
На практике часто применяется разложение функций в степенной ряд.
Ряд Тейлора.
(Пьер Альфонс Лоран (1813 – 1854) – французский математик)
Функция f(z), аналитическая в круге ![]() , разлагается в сходящийся к ней степенной ряд по степеням (z – z0).
, разлагается в сходящийся к ней степенной ряд по степеням (z – z0).
Коэффициенты ряда вычисляются по формулам:

![]()
Степенной ряд с коэффициентами такого вида называется рядом Тейлора.
Правая часть линейного неоднородного дифференциального уравнения имеет вид:
![]()
где ![]() - многочлен степени m.
- многочлен степени m.
Тогда частное решение ищется в виде:
![]()
Здесь Q(x)- многочлен той же степени, что и P(x), но с неопределенными коэффициентами, а r – число, показывающее сколько раз число a является корнем характеристического уравнения для соответствующего линейного однородного дифференциального уравнения.
Правая часть линейного неоднородного дифференциального уравнения имеет вид:
![]()
Здесь Р1(х) и Р2(х) – многочлены степени m1 и m2 соответственно.
Тогда частное решение неоднородного уравнения будет иметь вид:
![]()
где число r показывает сколько раз число ![]() является корнем характеристического уравнения для соответствующего однородного уравнения, а Q1(x) и Q2(x) – многочлены степени не выше m, где m- большая из степеней m1 и m2.
является корнем характеристического уравнения для соответствующего однородного уравнения, а Q1(x) и Q2(x) – многочлены степени не выше m, где m- большая из степеней m1 и m2.
Заметим, что если правая часть уравнения является комбинацией выражений рассмотренного выше вида, то решение находится как комбинация решений вспомогательных уравнений, каждое из которых имеет правую часть, соответствующую выражению, входящему в комбинацию.
Т.е. если уравнение имеет вид: ![]() , то частное решение этого уравнения будет
, то частное решение этого уравнения будет ![]() где у1 и у2 – частные решения вспомогательных уравнений
где у1 и у2 – частные решения вспомогательных уравнений
![]() и
и ![]()
Предельный признак Даламбера.
Предельный признак Даламбера является следствием из приведенного выше признака Даламбера.
Если существует предел ![]() , то при r < 1 ряд сходится, а при r > 1 – расходится. Если r = 1, то на вопрос о сходимости ответить нельзя.
, то при r < 1 ряд сходится, а при r > 1 – расходится. Если r = 1, то на вопрос о сходимости ответить нельзя.
Пример. Определить сходимость ряда ![]() .
.
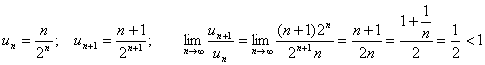
Вывод: ряд сходится.
Пример. Определить сходимость ряда ![]()
![]()
Вывод: ряд сходится.
Нормальные системы обыкновенных дифференциальных уравнений.
Определение. Совокупность соотношений вида:
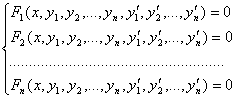
где х- независимая переменная, у1, у2,…,уn – искомые функции, называется системой дифференциальных уравнений первого порядка.
Определение. Система дифференциальных уравнений первого порядка, разрешенных относительно производных от неизвестных функций называется нормальной системой дифференциальных уравнений.
Такая система имеет вид:
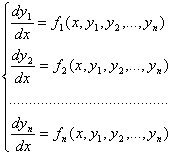 (1)
(1)
Для примера можно сказать, что график решения системы двух дифференциальных уравнений представляет собой интегральную кривую в трехмерном пространстве.
Теорема. (Теорема Коши). Если в некоторой области (n-1) –мерного пространства функции ![]()
![]() …
… ![]() непрерывны и имеют непрерывные частные производные по
непрерывны и имеют непрерывные частные производные по ![]() , то для любой точки
, то для любой точки ![]() этой области существует единственное решение
этой области существует единственное решение
![]()
системы дифференциальных уравнений вида (1), определенное в некоторой окрестности точки х0 и удовлетворяющее начальным условиям ![]()
Определение. Общим решением системы дифференциальных уравнений вида (1) будет совокупность функций ![]() ,
, ![]() , …
, … ![]() , которые при подстановке в систему (1) обращают ее в тождество
, которые при подстановке в систему (1) обращают ее в тождество
Ряды с неотрицательными членами.
При изучении знакопостоянных рядов ограничимся рассмотрением рядов с неотрицательными членами, т.к. при простом умножении на –1 из этих рядов можно получить ряды с отрицательными членами.
Теорема. Для сходимости ряда ![]() с неотрицательными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены.
с неотрицательными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены.
Признак сравнения рядов с неотрицательными членами.
Пусть даны два ряда ![]() и
и ![]() при un, vn ³ 0.
при un, vn ³ 0.
Теорема. Если un £ vn при любом n, то из сходимости ряда ![]() следует сходимость ряда
следует сходимость ряда ![]() , а из расходимости ряда
, а из расходимости ряда ![]() следует расходимость ряда
следует расходимость ряда ![]() .
.
Доказательство. Обозначим через Sn и sn частные суммы рядов ![]() и
и ![]() . Т.к. по условию теоремы ряд
. Т.к. по условию теоремы ряд ![]() сходится, то его частные суммы ограничены, т.е. при всех n sn < M, где М – некоторое число. Но т.к. un £ vn, то Sn £ sn то частные суммы ряда
сходится, то его частные суммы ограничены, т.е. при всех n sn < M, где М – некоторое число. Но т.к. un £ vn, то Sn £ sn то частные суммы ряда ![]() тоже ограничены, а этого достаточно для сходимости.
тоже ограничены, а этого достаточно для сходимости.
Также используется следующий признак сходимости:
Теорема. Если ![]() и существует предел
и существует предел ![]() , где h – число, отличное от нуля, то ряды
, где h – число, отличное от нуля, то ряды ![]() и
и ![]() ведут одинаково в смысле сходимости.
ведут одинаково в смысле сходимости.
Признак Коши. (радикальный признак)
Если для ряда ![]() с неотрицательными членами существует такое число q<1, что для всех достаточно больших n выполняется неравенство
с неотрицательными членами существует такое число q<1, что для всех достаточно больших n выполняется неравенство
![]() ,
,
то ряд ![]() сходится, если же для всех достаточно больших n выполняется неравенство
сходится, если же для всех достаточно больших n выполняется неравенство
![]()
то ряд ![]() расходится.
расходится.
Следствие. Если существует предел ![]() , то при r<1 ряд сходится, а при r>1 ряд расходится.
, то при r<1 ряд сходится, а при r>1 ряд расходится.
Интегральный признак Коши.
Если j(х) – непрерывная положительная функция, убывающая на промежутке (1;¥), то ряд j(1) + j(2) + …+ j(n) + … = ![]() и несобственный интеграл
и несобственный интеграл ![]() одинаковы в смысле сходимости.
одинаковы в смысле сходимости.
Пример. Ряд ![]() сходится при a>1 и расходится a£1 т.к. соответствующий несобственный интеграл
сходится при a>1 и расходится a£1 т.к. соответствующий несобственный интеграл ![]() сходится при a>1 и расходится a£1. Ряд
сходится при a>1 и расходится a£1. Ряд ![]() называется общегармоническим рядом.
называется общегармоническим рядом.
Следствие. Если f(x) и j(х) – непрерывные функции на интервале (a, b) и ![]() то интегралы
то интегралы 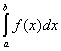 и
и 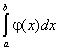 ведут себя одинаково в смысле сходимости.
ведут себя одинаково в смысле сходимости.
Знакочередующиеся ряды.
Знакочередующийся ряд можно записать в виде:
![]()
где ![]()
Признак Лейбница.
Если у знакочередующегося ряда ![]() абсолютные величины ui убывают
абсолютные величины ui убывают ![]() и общий член стремится к нулю
и общий член стремится к нулю ![]() , то ряд сходится.
, то ряд сходится.
Признаки Даламбера и Коши для знакопеременных рядов.
Пусть ![]() - знакопеременный ряд.
- знакопеременный ряд.
Признак Даламбера. Если существует предел 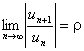 , то при r<1 ряд
, то при r<1 ряд ![]() будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
Признак Коши. Если существует предел ![]() , то при r<1 ряд
, то при r<1 ряд ![]() будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.
Пример. Разложить в ряд функцию ![]()
при помощи интегрирования.
При ![]() получаем по приведенной выше формуле:
получаем по приведенной выше формуле:
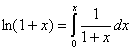
Разложение в ряд функции ![]() может быть легко найдено способом алгебраического деления аналогично рассмотренному выше примеру.
может быть легко найдено способом алгебраического деления аналогично рассмотренному выше примеру.
![]()
Тогда получаем: 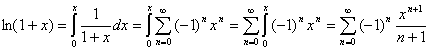
Окончательно получим: ![]()
Абсолютная и условная сходимость рядов.
Рассмотрим некоторый знакопеременный ряд (с членами произвольных знаков).
![]() (1)
(1)
и ряд, составленный из абсолютных величин членов ряда (1):
![]() (2)
(2)
Теорема. Из сходимости ряда (2) следует сходимость ряда (1).
Доказательство. Ряд (2) является рядом с неотрицательными членами. Если ряд (2) сходится, то по критерию Коши для любого e>0 существует число N, такое, что при n>N и любом целом p>0 верно неравенство:
![]()
По свойству абсолютных величин:
![]()
![]()
То есть по критерию Коши из сходимости ряда (2) следует сходимость ряда (1).
Определение. Ряд ![]() называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд ![]() .
.
Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают.
Определение. Ряд ![]() называется условно сходящимся, если он сходится, а ряд
называется условно сходящимся, если он сходится, а ряд ![]() расходится.
расходится.
Свойства абсолютно сходящихся рядов.
1) Теорема. Для абсолютной сходимости ряда ![]() необходимо и достаточно, чтобы его можно было представить в виде разности двух сходящихся рядов с неотрицательными членами.
необходимо и достаточно, чтобы его можно было представить в виде разности двух сходящихся рядов с неотрицательными членами.
Следствие. Условно сходящийся ряд является разностью двух расходящихся рядов с неотрицательными стремящимися к нулю членами.
2) В сходящемся ряде любая группировка членов ряда, не изменяющая их порядка, сохраняет сходимость и величину ряда.
3) Если ряд сходится абсолютно, то ряд, полученный из него любой перестановкой членов, также абсолютно сходится и имеет ту же сумму.
Перестановкой членов условно сходящегося ряда можно получить условно сходящийся ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
4) Теорема. При любой группировке членов абсолютно сходящегося ряда (при этом число групп может быть как конечным, так и бесконечным и число членов в группе может быть как конечным, так и бесконечным) получается сходящийся ряд, сумма которого равна сумме исходного ряда.
5) Если ряды ![]() и
и ![]() сходятся абсолютно и их суммы равны соответственно S и s, то ряд, составленный из всех произведений вида
сходятся абсолютно и их суммы равны соответственно S и s, то ряд, составленный из всех произведений вида ![]() взятых в каком угодно порядке, также сходится абсолютно и его сумма равна S×s - произведению сумм перемножаемых рядов.
взятых в каком угодно порядке, также сходится абсолютно и его сумма равна S×s - произведению сумм перемножаемых рядов.
Если же производить перемножение условно сходящихся рядов, то в результате можно получить расходящийся ряд.
Тригонометрический ряд.
Определение. Тригонометрическим рядом называется ряд вида:
![]()
или, короче, ![]()
Действительные числа ai, bi называются коэффициентами тригонометрического ряда.
Если ряд представленного выше типа сходится, то его сумма представляет собой периодическую функцию с периодом 2p, т.к. функции sinnx и cosnx также периодические функции с периодом 2p.
Пусть тригонометрический ряд равномерно сходится на отрезке (-p; p), а следовательно, и на любом отрезке в силу периодичности, и его сумма равна f(x).
Определим коэффициенты этого ряда.
Для решения этой задачи воспользуемся следующими равенствами:
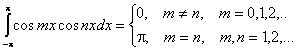
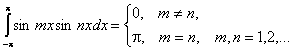
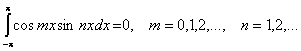
Справедливость этих равенств вытекает из применения к подынтегральному выражению тригонометрических формул. Подробнее см. Интегрирование тригонометрических функций.
Т.к. функция f(x) непрерывна на отрезке (-p; p), то существует интеграл
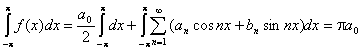
 Такой результат получается в результате того, что
Такой результат получается в результате того, что 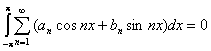 .
.
Получаем: 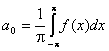
Далее умножаем выражение разложения функции в ряд на cosnx и интегрируем в пределах от -p до p.
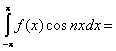
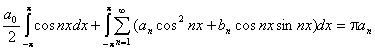
Отсюда получаем: 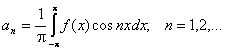
Аналогично умножаем выражение разложения функции в ряд на sinnx и интегрируем в пределах от -p до p.
Получаем: 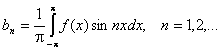
Выражение для коэффициента а0 является частным случаем для выражения коэффициентов an.
Таким образом, если функция f(x) – любая периодическая функция периода 2p, непрерывная на отрезке (-p; p) или имеющая на этом отрезке конечное число точек разрыва первого рода, то коэффициенты
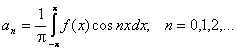
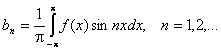
существуют и называются коэффициентами Фурье для функции f(x).
Определение. Рядом Фурье для функции f(x) называется тригонометрический ряд, коэффициенты которого являются коэффициентами Фурье. Если ряд Фурье функции f(x) сходится к ней во всех ее точках непрерывности, то говорят, что функция f(x) разлагается в ряд Фурье.
Функциональные ряды.
Определение. Частными (частичными) суммами функционального ряда ![]() называются функции
называются функции ![]()
Определение. Функциональный ряд ![]() называется сходящимся в точке (х=х0), если в этой точке сходится последовательность его частных сумм. Предел последовательности
называется сходящимся в точке (х=х0), если в этой точке сходится последовательность его частных сумм. Предел последовательности ![]() называется суммой ряда
называется суммой ряда ![]() в точке х0.
в точке х0.
Определение. Совокупность всех значений х, для которых сходится ряд ![]() называется областью сходимости ряда.
называется областью сходимости ряда.
Определение. Ряд ![]() называется равномерно сходящимся на отрезке (a,b), если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
называется равномерно сходящимся на отрезке (a,b), если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
Теорема. (Критерий Коши равномерной сходимости ряда)
Для равномерной сходимости ряда ![]() необходимо и достаточно, чтобы для любого числа e>0 существовал такой номер N(e), что при n>N и любом целом p>0 неравенство
необходимо и достаточно, чтобы для любого числа e>0 существовал такой номер N(e), что при n>N и любом целом p>0 неравенство
![]()
выполнялось бы для всех х на отрезке (a,b).
Определение. Рядом Фурье для функции f(x) называется тригонометрический ряд, коэффициенты которого являются коэффициентами Фурье. Если ряд Фурье функции f(x) сходится к ней во всех ее точках непрерывности, то говорят, что функция f(x) разлагается в ряд Фурье.
Достаточные признаки разложимости в ряд Фурье.
Теорема. (Теорема Дирихле) Если функция f(x) имеет период 2p и на отрезке
(-p;p) непрерывна или имеет конечное число точек разрыва первого рода, и отрезок
(-p;p) можно разбить на конечное число отрезков так, что внутри каждого из них функция f(x) монотонна, то ряд Фурье для функции f(x) сходится при всех значениях х, причем в точках непрерывности функции f(x) его сумма равна f(x), а в точках разрыва его сумма равна ![]() , т.е. среднему арифметическому предельных значений слева и справа. При этом ряд Фурье функции f(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f(x).
, т.е. среднему арифметическому предельных значений слева и справа. При этом ряд Фурье функции f(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f(x).
Функция f(x), для которой выполняются условия теоремы Дирихле называется кусочно – монотонной на отрезке (-p;p).
Теорема. Если функция f(x) имеет период 2p, кроме того, f(x) и ее производная f’(x) – непрерывные функции на отрезке (-p;p) или имеют конечное число точек разрыва первого рода на этом отрезке, то ряд Фурье функции f(x) сходится при всех значениях х, причем в точках непрерывности его сумма равна f(x), а в точках разрыва она равна ![]() . При этом ряд Фурье функции f(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f(x).
. При этом ряд Фурье функции f(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f(x).
Функция, удовлетворяющая условиям этой теоремы, называется кусочно – гладкой на отрезке (-p;p).
Разложение в ряд Фурье непериодической функции.
Задача разложения непериодической функции в ряд Фурье в принципе не отличается от разложения в ряд Фурье периодической функции.
Допустим, функция f(x) задана на отрезке (a, b) и является на этом отрезке кусочно – монотонной. Рассмотрим произвольную периодическую кусочно – монотонную функцию f1(x) c периодом 2Т ³ ïb-aï, совпадающую с функцией f(x) на отрезке (a, b).
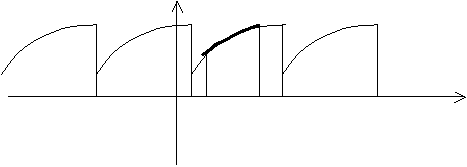 y
y
f(x)
a - 2T a a b a+2T a + 4T x
Таким образом, функция f(x) была дополнена. Теперь функция f1(x) разлагается в ряд Фурье. Сумма этого ряда во всех точках отрезка (a, b) совпадает с функцией f(x), т.е. можно считать, что функция f(x) разложена в ряд Фурье на отрезке (a, b).
Таким образом, если функция f(x) задана на отрезке, равном 2p ничем не отличается от разложения в ряд периодической функции. Если же отрезок, на котором задана функция, меньше, чем 2p, то функция продолжается на интервал (b, a + 2p) так, что условия разложимости в ряд Фурье сохранялись.
Вообще говоря, в этом случае продолжение заданной функции на отрезок (интервал) длиной 2p может быть произведено бесконечным количеством способов, поэтому суммы получившихся рядов будут различны, но они будут совпадать с заданной функцией f(x) на отрезке (a,b)
Свойства равномерно сходящихся рядов.
1) Теорема о непрерывности суммы ряда.
Если члены ряда ![]() - непрерывные на отрезке (a,b) функции и ряд сходится равномерно, то и его сумма S(x) есть непрерывная функция на отрезке (a,b).
- непрерывные на отрезке (a,b) функции и ряд сходится равномерно, то и его сумма S(x) есть непрерывная функция на отрезке (a,b).
2) Теорема о почленном интегрировании ряда.
Равномерно сходящийся на отрезке (a,b) ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку (a,b) , сходится к интегралу от суммы ряда по этому отрезку.
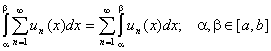
3) Теорема о почленном дифференцировании ряда.
Если члены ряда ![]() сходящегося на отрезке (a,b) представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных
сходящегося на отрезке (a,b) представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных ![]() сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно.
![]()
На основе того, что сумма ряда является некоторой функцией от переменной х, можно производить операцию представления какой – либо функции в виде ряда (разложения функции в ряд), что имеет широкое применение при интегрировании, дифференцировании и других действиях с функциями.
На практике часто применяется разложение функций в степенной ряд
Теорема. (Признак равномерной сходимости Вейерштрасса)
(Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик)
Ряд ![]() сходится равномерно и притом абсолютно на отрезке (a,b), если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :
сходится равномерно и притом абсолютно на отрезке (a,b), если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :
![]()
т.е. имеет место неравенство:
![]() .
.
Еще говорят, что в этом случае функциональный ряд ![]() мажорируется
мажорируется