Производная и ее применение в алгебре, геометрии, физике
0.Периметр убывает в промежутке 0 Следовательно, периметр прямоугольника имеет наименьшее значение (минимум), если длина его 6 м и ширина 36/6 м = 6 м, т. е. когда он квадрат. Задачи на отыскание наибольших и наименьших значений величин имеют важное значение в технике и, как это ясно из примеров, сводятся к отысканию максимума и минимума функции. 2. Функция f(x) имеет при x= с минимум, если ее значение при х=с меньше, чем при любом другом значении х, взятом в некоторой окрестности точки х=с. Термины "максимум" и "минимум" объединяются в один общий для них термин "экстремум". Значение аргумента, которое дает максимум (или минимум) функции, называется точкой максимума (минимума), или точкой экстремума. Функция может иметь только максимум, например функция y = 60x— 2х2 (черт. 111), или только минимум, например функция у = 2х+72/x (черт. 112), или иметь максимум и минимум, как, например, функция у = х3— — х2 — 8х+2 (черт. 108). Функция может иметь несколько максимумов и минимумов (черт. 113), причем в этом случае максимумы и минимумы чередуются. Функция может не иметь ни максимума, ни минимума. Например, функции у = х3, y = ctgx, y = ax не имеют ни максимума, ни минимума, так как при возрастании х от — ∞ до +∞ первая и третья функции возрастают, а вторая только убывает. 1°. Теорема (необходимый признак). Если в окрестности 2δ точки х=с: 1) функция f(х) дифференцируема, 2) значение х=с есть точка экстремума функции f(x), то ее производная в точке с равна нулю, m. e. f '(c) = 0. Доказательство. Пусть для определенности х=c есть точка максимума (черт. 111). Представим значения независимого переменного х левой полуокрестности точки с в виде с — Δx:, а правой в виде с+ Δx, где 0< Δx < δ. Значение функции f(x) в точке с есть f(c), в левой полуокрестности оно равно f(с — Δx), а в правой f(c + Δx). Значения f(x) в окрестности 2δ точки с поставлены, таким образом, в зависимость от значений Δx, причем значение х = с -/+ Δx неограниченно приближается к числу с, если Δx стремится к нулю. По определению максимума функции: f(c- Δx) Отсюда: f(c-Δx)-f(c)<0 и f(c + Δx)-f(с)<0. Левые части неравенств выражают приращение функции в точке х = с при изменении аргумента соответственно на — Δx и + Δx. Составив отношение приращения функции к приращению аргумента, получаем: lim ((f(c - Δx)-f(c))/(—Δx)) = f‘(c) и lim ((f(c + Δx)-f(c))/(+Δx)) = f‘(c). - Δx→0 + Δx→0 Из неравенства (1) следует, что f '(с) либо положительна, либо равна нулю, а неравенство (2) показывает, что f '(с) не может быть положительной. Следовательно, f‘(c) = 0, что и требовалось доказать. 2°. Теорема (достаточный признак). Если в окрестности 2δ точки x = с: 1) функция f(x) непрерывна, 2) ее производная, f '(х), слева от точки х = с положительна, а справа отрицательна, то значение х = с есть точка максимума функции. lim f(c - Δx) = f(c) и lim f(c + Δx) = f(c). - Δx→0 + Δx→0Если х = →0 3 4 5 6 7 8 →∞ То у = →∞ 30 26 24,4 24 24,3 25 →∞ Максимум и минимум функции
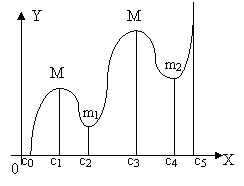Определение. 1. Функция f(x) имеет при х=с максимум, если ее значение при х=с больше, чем при любом другом значении х, взятом в некоторой окрестности точки х=с.
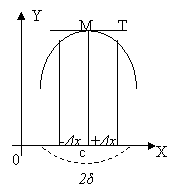Максимум (минимум) функции может не быть наибольшим (наименьшим) значением ее. Так, изображенная на черт. 113 функция имеет в точке с. значение, большее максимумов с1М1 и с3М2, а в точке с0 значение, меньшее минимума c2m1, и c4m2, минимум c4m2 больше максимума с1М1. Максимум (минимум) функции в данной точке вообще есть наибольшее (наименьшее) значение функции по сравнению с ее значениями в точках, лежащих слева и справа от точки экстремума лишь в достаточной близости к ней.Признаки существования экстремума
(f(c —Δx)—f(с))/(-Δx))>0 (1); (f(с + Δx)—f(с)/(+Δx))<0 (2) Оба отношения (1) и (2) имеют один и тот же предел при Δx → 0, так как по условно функция f(x) имеет в точке с определенную произвольную:
Доказательство. Данная функция непрерывна в точке c, поэтому число f(с) есть общий предел для f(c — Δx) и f(c+Δx) при Δx → 0 (как и в предыдущей теореме, здесь и в последующем 0 < Δx< δ):
Данная функция f(x) в левой полуокрестности точки с — возрастающая, так как ее производная слева от точки с положительна, а в правой полуокрестности — убывающая, так как ее производная справа от точки с отрицательна (черт.), и вследствие этого ее значения
f(c —Δx) и f(c+Δx)
Другими словами, как f(c — Δx), так и f(c+Δx) приближаются к своему пределу f(с) так, что для каждого значения Δx ≠ 0: f(c - Δx) < f(c) и f(c + Δx) < f(c). Но в таком случае f(c) есть максимум функции f(x) в точке х = с. 3°. Так же можно доказать, что если в окрестности 2δ точки х = с: 1) функция f(x) непрерывна, 2) производная f '(x) слева от точки х = с отрицательна, а справа положительна, то значение х = с есть точка минимума функции (черт.). 4°. Как в точке максимума, так и в точке минимума производная равна нулю (1°). Обратное неверно. Функция может не иметь ни максимума, ни минимума в точке, в которой производная равна нулю. Например, функция у = х3 имеет в точке x =0 производную, равную нулю. Однако в точке х = 0 нет ни максимума, ни минимума, функция у = х3 при всех значениях х, в том числе и при x = 0, возрастает. Отсюда, в точке х=с функция f(x) не имеет на максимума, ни минимума, если при х = с ее производная равна нулю и имеет один и тот же знак как слева, так и справа от точки х = с. 5°. Определение. Значения аргумента х, при которых производная f '(х) равна нулю, называются стационарными точками. Касательная в стационарных точках параллельна оси Ох. В окрестности точки максимума касательная составляет с осью абсцисс острый угол, если точка лежит слева от точки максимума, и тупой угол, если справа от нее (черт.). В случае минимума, напротив, касательная составляет с осью абсцисс тупой угол, если точка находится слева от точки минимума, и острый, если справа от нее (черт.). 1°. Чтобы найти экстремум функции, надо: 1) найти производную данной функции; 2) приравнять производную нулю и решить полученное уравнение; из полученных корней отобрать действительные и расположить их (для удобства) по их величине от меньшего к большему; в том случае, когда все корни оказываются мнимыми, данная функция не имеет экстремума; 3) определить знак производной в каждом из промежутков, отграниченных стационарными точками; 4) если производная положительна в промежутке, лежащем слева от данной стационарной точки, и отрицательна в промежутке, лежащем справа от нес, то данная точка есть точка максимума функции, если же производная отрицательна слева и положительна справа от данной стационарной точки, то данная точка есть точка минимума функции; если производная имеет один и тот же знак как слева, так и справа от стационарной тонки, то в этой точке нет ни максимума, ни минимума, функции; 5) затенить в данном выражении функции аргумент значением, которое дает максимум или минимум функции; получим значение соответственно максимума или минимума функции. Если функция имеет точки разрыва, то эти точки должны быть включены в число стационарных точек, разбивающих Ох на промежутки, в которых определяется знак производной. 1°. Лемма. Если при х = с производная положительна (или отрицательна), то в достаточно малой окрестности точки х = с приращение функции и приращение аргумента в точке с имеют одинаковые (или разные) знаки. lim (∆y/∆x)>0. ∆x→0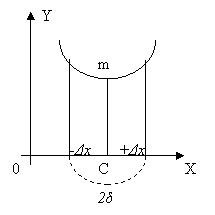
возрастают при стремлении Δx к нулю (по определению убывающей функции, меньшему значению аргумента отвечает большее значение функции, т. е. при x1>x2 f(x1)Правило нахождения экстремума
Нахождение экстремума при помощи второй производной
Доказательство от противного. Пусть для определенности f '(c)>0, т. е.
Предположим, что при стремлении ∆x к нулю приращения ∆y и ∆x имеют разные знаки. Тогда отношение ∆y/∆x отрицательно и его предел
f '(c) ≤ 0,
что противоречит условию.
Так же доказывается и вторая часть леммы.
2°. Теорема. Если при х = с первая производная функции f(x) равна нулю, f '(c)=0, а вторая производная положительна, f "(c)>0, то в точке х = с функция f(x) имеет минимум;
если же вторая производная отрицательна, f "(с) < 0, то в точке х = с функция f(x) имеет максимум.
f ’’(c) = lim ((f’(c + ∆x)-f ’(c))/∆x)>0. ∆x→0 |
Согласно лемме, если при х = с производная (в данном случае вторая) положительна, то в достаточно малой окрестности 2δ точки с приращение функции (в данном случае первой производной) имеет тот же знак, что и приращение аргумента. Слева от точки с приращение аргумента отрицательно, значит, и приращение функции отрицательно, т.е.
f '(c — ∆x)—f(c)<0, (0 < ∆x < δ).
Отсюда:
f '(c-∆x) Справа от точки с приращение аргумента положительно, т. е. f '(c +∆x)-f '(c)>0. Отсюда: f '(c + ∆x)>f '(c) = 0. (2) Получили: первая производная функции f(x) слева от точки с отрицательна (1), а справа положительна (2). Значит, в точке х = с функция f(x) имеет минимум, как это и требовалось доказать. Так же доказывается теорема и в случае f "(с)<0. 3°. Доказанная теорема определяет второй способ нахождения экстремума. Он отличается от первого тем, что третья и четвертая операции первого способа заменяются: а) нахождением второй производной и б) определением ее знака в стационарной точке. Результат исследования можно выразить так: плюс минус минимум максимум Если f '(с) = 0, то исследование функции на максимум и минимум надо провести первым способом. 4°. Пример 1. Исследовать вторым способом на максимум и минимум функцию: у = 5 — х2 — х3 — x4/4. Решение. 1. Находим первую производную: y ' = - 2х - Зx2 — x3 2. Приравниваем первую производную нулю и решаем полученное уравнение: — 2x — Зx2 — x3 = 0, или x(x2+3х+2) = 0, отсюда x = 0 или x2+ 3х + 2 = 0. Решая квадратное уравнение x2 + 3х + 2 = 0, получаем: x = (-3 + 1)/2. Стационарных точек три: x1 = — 2, x2 = — 1 и х3 = 0. 3. Находим вторую производную: у" = — 2 - бx — Зx2. 4. Определяем знак второй производной, заменяя х его значением сначала в первой, затем во второй и потом в третьей стационарной точке: при х = — 2 у'' = — 2 — 6(— 2) — 3(— 2)2 = — 2, при х = — 1 у" = — 2 — 6(— 1) — 3(— l)2 = + 1, при x = 0 у" = — 2. Следовательно, данная функция имеет минимум при х = —1 и максимум при х = — 2 и при х =0, Пример 2, Исследовать на максимум и минимум функцию: у = х4. Решение: 1) y' = 4x3; 2) 4х3 = 0; х = 0; 3) y" = 12x2; 4) при х = 0 y" = 0. Так как оказалось, что вторая производная равна нулю, то исследование ведем первым способом: при х < 0 у' = 4x3 < 0, а при х > 0 у' = 4x3 > 0. Следовательно, функция у = х4 имеет минимум в точке x = 0. 5°. Второй способ нахождения экстремума имеет смысл применять в том случае, когда вторая производная отыскивается просто; если же дифференцирование сопровождается трудными преобразованиями и не упрощает выражение первой производной, то первый способ может быстрее привести к цели. Пусть две точки M1 и M2 имеют одну и ту же абсциссу. Если при этом ордината точки M1 более (менее) ординаты точки M2, то говорят, что точка M1 лежит выше (ниже) точки M2. Говорят также, что в промежутке а<х f(x)> φ(x) (или f(x)< φ(x)). Определение. В промежутке а < х < b кривая— график дифференцируемой функции y=f(x) — называется вогнутой вверх (вниз), если она лежит выше (ниже) касательной в любой точке данного промежутка. 2°. В более подробных курсах анализа доказывается, что если производная f '(х) — возрастающая (убывающая) функция в промежутке а < х < b, то кривая y=f(х) является вогнутой вверх (вниз) в этом промежутке. Чтобы уяснить эту теорему, наметим на оси Ох (черт.) произвольно ряд точек и проведем через каждую из них прямую так, чтоб и угловом коэффициент прямой возрастал с возрастанием абсциссы намеченных точек; затем, приняв эти прямые за касательные к некоторой кривой линии (tgφ = f '(x)), построим эту кривую линию. Мы видим, что она может лежать только выше каждой из проведенных касательных. 3°. Достаточный признак вогнутости вверх (вниз). Если в промежутке а<х Действительно, если в промежутке а<х Если f "(x) = 0 не в отдельных точках, а в некотором промежутке, то в этом промежутке f '(x) — постоянная функция, a f(x) — линейная функция, график ее — прямая линия, и говорить о вогнутости не имеет смысла. 1°. Определение, Если в некоторой окрестности точки х = с кривая —график дифференцируемой функции y = f(x) — имеет слева и справа от точки х = с вогнутости противоположного направления, то значение х = с называется точкой перегиба. 2°. Так как слева и справа от точки перегиба х = с вогнутости кривой y=f(x) разного направления, то вторая производная f "(x) имеет слева и справа от точки х = с разные знаки или равна нулю. Полагая вторую производную непрерывной и окрестности точки х = с, заключаем, что в точке перегиба она равна нулю, т. е. f(c) = 0. 3°. Отсюда следует правило нахождения точек перегиба: 1) найти вторую производную данной функции; 2) приравнять ее нулю и решить полученное уравнение (или найти те значения х, при которых производная теряет числовой смысл), из полученных корней отобрать действительные и расположить их no величине от меньшего к большему; 3) определить знак второй производной в каждом, из промежутков, отграниченных полученными корнями; 4) если при этом в двух промежутках, отграниченных исследуемой точкой, знаки второй производной окажутся разными, то имеется точка перегиба, если одинаковыми, то точки перегиба нет. 4°. Примеры. Найти точки перегиба и определить промежутки вогнутости вверх и вниз кривых: 1) у = lп х. Р е ш е н и е. Находим вторую производную: y '=1/x; y ''= -1/x2. При всяком значении x = (0 < х <+∞) у" отрицательна. Значит, логарифмика точек перегиба не имеет и обращена вогнутостью вниз. 2) у = sin x. Решение. Находим вторую производную: y' =cos x, y'' = -sin x. Полагая - sin x = 0, находим, что x = kπ, где k - целое число. Если 0 < x< π, то sin x положителен и y '' отрицательна, если же π < x< 2π, то sin x отрицателен и y'' положительна и т. д. Значит, синусоида имеет точки перегиба 0, π, 2π,... В первом промежутке 0 < x< π она обращена вогнутостью вниз, во втором - вогнутостью вверх и т. д. Предположим, что точка движется прямолинейно и пройденный ею путь определяется уравнением s = f(t), где t время. Скорость v в момент времени t есть производная от пути по времени, т. е. v=ds/dt. Скорость изменения скорости в момент времени t есть ускорение а, a=(v)' = (ds/dt)' = (d2s/dt2). Вторая производная от пути по времени есть ускорение прямолинейного движения в данный момент времени. Пример. Прямолинейное движение точки совершается по закону: s = (t3 — 2) м. Определить ускорение в момент t = 10 сек. Решение. Ускорение а = d2s/dt2. Дифференцируя функцию s=t3 — 2, находим d2s/dt2 =6t Следовательно, a = 6t = 6*10 = 60; a = 60 мсек2. 2°. Если движение неравномерное, то сила F, производящая его, непостоянна, каждому моменту времени t соответствует определенное значение действующей силы F, и сила, таким образом, есть функция времени t, F=f(t). По закону Ньютона, в каждый момент времени действующая сила F равна произведению массы т на ускорение а, т. е. F=ma, или f(t) = ma. При прямолинейном движении a =d2s/dt2, поэтому f(t) = m*d2s/dt2. Зная уравнение прямолинейного движения, можно дифференцированием найти значение действующей силы в каждый момент времени. Пример. Определить силу, под действием которой материальная точка совершает прямолинейные колебания по закону s = А*sin(ωt + ω0). Решение. f(f) = m*d2s/dt2, поэтому находим вторую производную функции: s = А*sin(ωt + ω0), ds/dt = А*cos(ωt+ω0)* ω, d2s/dt2=— А*sin (ωt + ω0)* ω2 = — s*ω2 = — ω2s; f(t) = — mω2s, т. е. рассматриваемые колебания совершаются под действием силы, пропорциональной перемещению s и направленной в противоположную сторону. 1°. Составим отношение бесконечно малых, приближающихся к нулю по различным законам, так что каждому рассматриваемому моменту приближения к нулю одной из бесконечно малых отвечает определенное значение каждой из рассматриваемых бесконечно малых. Например, пусть в те моменты приближения к нулю, когда значения α = 10;1; 0.1; 0,01 и т.д.; значения β =1000; 1; 0,001; 0,000001 и т.д. Отношение β/α =100; 1; 0, 01; 0, 0001 и т.д., т.е. значение отношения бесконечно малых не остается неизменным в процессе приближения их к нулю. Отношение бесконечно малых, таким образом,—величина переменная, и у нее может существовать предел, конечный (равный нулю, как в примере, или отличный от нуля) или бесконечный, а может предела и не существовать. 2°. Определения: 1) β называется бесконечно малой высшего порядка малости, чем α, если предел отношения β/α равен нулю, т. е. если limβ/α =0; 2) β называется бесконечно малой низшего порядка малости, чем α, если limβ/α = ∞; 3) β и α называются бесконечно малыми одинакового порядка малости, если предел их отношения есть число k, отличное от нуля, т. е. если limβ/α = k, где k ≠ 0 и k ≠ ∞ 4) β и α называются несравнимыми бесконечно малыми, если предела их отношения не существует. 3°. Примеры. 1. В рассмотренном выше примере limβ/α = 0, β высшего порядка малости, чем α, a limα/β = ∞ и α низшего порядка, чем β. lim (β/α) = lim (1+x) =2. х→1Если знак числа f "(с), то при х = с f(x) имеет Направление вогнутости кривой
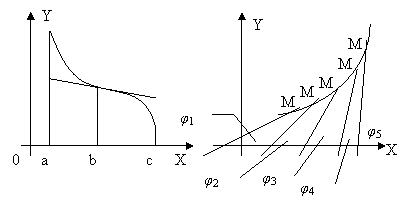Кривая, изображенная на черт., является вогнутой, вверх в промежутке а < х < b и вогнутой вниз в промежутке b < х < с.Точки перегиба
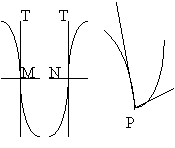Точку М кривой (черт.), абсцисса которой х = с, называют также точкой перегиба, она отделяет дугу кривой, вогнутую вверх, от дуги, вогнутой вниз. Точкой перегиба может быть только та точка, в которой к кривой имеется касательная. В окрестности точки перегиба кривая лежит по обе стороны от касательной: выше и ниже ее. Заметим, что она расположена также по обе стороны от нормали. Но такая точка, как Р (черт.), в которой единственной касательной не имеется, точкой перегиба не является.Механическое значение второй производной
Дифференциал
Сравнение бесконечно малых
2. α =1—х и β=1— x2 —бесконечно малые, если х→1. Отношение β/α=(1- x2)/(1-x) = 1+x.
Значит, 1—х и 1—x2 —бесконечно малые одинакового порядка малости при х→1.
3. Сравним 1 —cosx с х при x→ 0.
lim((1-cosx)/x) = lim((2sin2(x/2))/x) = lim((sin(x/2))*sin(x/2)/(x/2))= x→0 x→0 x/2→0 =lim((sin(x/2))/(x/2))*lim(sin(x/2)) = 1*0 = 0 x/2→0 x/2→0 |
т. е. 1—cos x при х → 0 есть бесконечно малая высшего порядка малости, чем х.
Дифференциал функции
1°. Определение. Дифференциалом (dy) функции y=f(x) называется произведение значения производной f '(х) на произвольное приращение ∆x аргумента х, т. е.
| dy=f '(x)*∆x |
(I)
2°. Для получения значения дифференциала функции необходимо знать два числа: начальное значение аргумента, х, и его приращение, ∆x.
Пример. Вычислить дифференциал функции у = x2 при изменении значения аргумента х от 3 до 3,1.
Решение. dy=f '(х)* ∆х. Найдем dy сначала для произвольных значений х и ∆x.
f '(x) = (x2)' =2x.
Поэтому
dy=2x*∆x.
Начальное значение аргумента х=3, приращение его ∆x = 3,1 — 3 = 0,1. Подставляя эти значения в выражение dy находим:
dy =2*3*0,1=0,6.
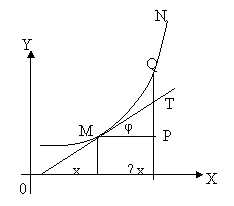Для данного значения независимого переменного х дифференциал функции f(x) есть линейная функция приращения независимого переменного ∆х.
3°. Рассмотрим геометрический смысл дифференциала функции. На черт. в точке х проведена касательная к графику функции y=f(x). Из ∆MPT следует, что
PT = MP*tgφ = ∆x*f '(x).
Но по определению f '(х) *∆x = dy, поэтому PT = dy.
Дифференциал функции f(x) при данном значении х геометрически выражается приращением ординаты касательной к графику функции y=f(x) в точке х.
4°. Дифференциал dy и приращение ∆у вообще не равны между собой. На черт. dy = PT менее ∆y=PQ.
Очевидно, dy может быть и более ∆y. Это будет, например, если поднимающаяся кривая MN будет вогнута вниз.
5°. Пример. Для функции у=x2 при изменении х от 3 до 3,1 приращение ∆y = 2x*∆x + + ∆x2 = 2*3*0,1 + 0, 12 = 0, 61 Дифференциал dy = 2х *∆x = 2*3 * 0, 1 = 0,6. Принимая dy за приближенное значение ∆у, имеем: абсолютная погрешность приближения равна разности ∆у—dy=0,01, а относительная погрешность приближения есть отношение:
(∆y—dy)/dy=00,1/0,60=1,7%
6°. Разность между приращением и дифференциалом функции, ∆у—dy, высшего порядка малости, чем приращение аргумента, ∆x.
Действительно, отношение ∆y/∆x отличается от своего предела f '(x) на бесконечно малую α, причем α → 0 при стремлении ∆x к нулю,
∆y/∆x — f '(x)= α.
Производя вычитание в левой части равенства, получаем:
(∆y-f '(x)*∆x)/∆x = α, или (∆у - dy) ∆x= α,
lim((∆y-dy)/ ∆x) = lim α = 0. ∆x → 0 ∆x → 0 |
7°. Из сказанного следует: дифференциал функции есть приближенное значение ее приращения с относительной погрешностью, стремящейся к нулю вместе с приращением аргумента.
8°. Из изложенного следует, что дифференциал dy функции y=f(x) обладает двумя свойствами:
1) dy пропорционален ∆x (dy = k∆x, где k=y');
2) отношение (∆y—dy)/∆x стремится к нулю при стремлении ∆x к нулю.
Обратно. Если величина z обладает двумя свойствами:
1) z=k∆x и 2) то z есть дифференциал функции у.
Доказательство. Внося из (1) значение z во (2), имеем:
т. е. k = y',
а следовательно,
z = k∆x = y’∆x,
т. е. z есть дифференциал функции у.
Таким образом, эти два условия полностью определяют дифференциал.
Дифференциал аргумента. Производная как отношение дифференциалов
1°. Определение. Дифференциалом (dx) аргумента х называется, его приращение, ∆x:
dx = ∆х (II)
Может быть, некоторым основанием к этому служит то, что дифференциал функции у=х и приращение ее аргумента совпадают. Действительно,
dy = (x)' ∆x, или dy = ∆x.
Но так как
dy = dx, то dx = ∆x,
т.е. дифференциал функции у =х и приращение ее аргумента совпадают.
2°. Внеся в формулу (I) значение ∆x=dx, получаем:
| dy = f ’(x)*dx, |
(III)
т. е. дифференциал функции есть произведение ее производной на дифференциал аргумента.
3°. Формула (III) обладает замечательным свойством, именно: формула dy = f '(x)dx справедлива и в том случае, если x не является независимой переменной величиной, а является функцией другого аргумента, например и.
Действительно, если х есть функция от и, то f(x) есть сложная функция от u приращение dx обусловлено приращением ∆u, и dy надо вычислять по формуле;
dy = f 'u (x)* ∆u.
Но
f 'u (x)= f’x (x)* x’u
Значит,
dy = f’(x)—x'u * ∆u.
Но так как, по определению,
x'u ∆u = dx,
то, следовательно,
dy = f '(x)dx.
4°. Пример. Найти дифференциал функции:
_____________________
у = √ (e2x—1).
Решение. По формуле (III)
dy = у'*dx.
Находим у': ________ ________
y’ = e2x*2/( 2√ (e2x—1)) = e2x/ √ (e2x—1).
Значит _______
dy = e2x*dx/ √ (e2x—1)
5°. Из формулы (III) следует;
f’(x)=dy/dx,
т. е. производная функции равна отношению дифференциала функции к дифференциалу аргумента. Это иллюстрирует черт., где
dy/dx = PT/MP = tgφ=f '(x)
для произвольного значения dx = MP.
Приложения понятия дифференциала к приближенным вычислениям
1°. Разность ∆y—dy—бесконечно малая высшего порядка малости, чем ∆x, поэтому при достаточно малом ∆x
| ∆y ≈ dy =f '(х)∆x |
(IV)
Это означает, что при малых изменениях аргумента (от начального значения х) величину изменения функции y=f(x) можно приближенно считать пропорциональной величине изменения аргумента с коэффициентом пропорциональности, равным значению производной f '(x); кривую y=f (x) при этом можно приближенно заменить касательной к ней в точке х.
Так как ∆у = f(х + ∆x)—f (x), то, заменяя в формуле (IV) ∆у его выражением, имеем: f(x+∆x) - f(x) ≈ f '(x)* ∆x
| f(x+∆x) ≈ f(x) + f '(x)* ∆x |
(V)
В математике производную применяют для:
Исследования функции на монотонность, экстремумы.
Нахождения касательной к графику.
Нахождения наибольших, наименьших значений функций.
Нахождения дифференциала для приближенных вычислений.
Для доказательства неравенств.
Рассмотрю некоторые примеры применения производной в алгебре, геометрии и физике.
Задача 1. Найти сумму 1+2*1/3+3(1/3)2+…+100(1/3)99;
Решение.
Найду сумму g(x)=1+2x+3x2+…+100x99 и подставлю в нее x=1/3.
Для этого потребуется вспомогательная функция f(x)=x+x2+…+x100.
Ясно, что f ’(x)=g(x).
f(x) — сумма геометрической прогрессии.
Легко подсчитать, что f(x)=(x—x101)/(1—x). Значит,
g(x) = f ’(x) = ((1—101x100)(1—x)—(x—x100)(-1))/(1—x)2=(1—102x100+101x101)(1—x)2.
Подставлю x = 1/3.
Ответ: 0,25(9—205*3-99)
Задача 2. Найти сумму 1+2*3+3*32+…+100*399;
Решение.
Найду сумму g(x)=1+2x+3x2+…+100x99 и подставлю в нее x=1/3.
Для этого потребуется вспомогательная функция f(x)=x+x2+…+x100.
Ясно, что f ’(x)=g(x).
f(x) — сумма геометрической прогрессии.
Легко подсчитать, что f(x)=(x—x101)/(1—x). Значит,
g(x) = f ’(x) = ((1—101x100)(1—x)—(x—x100)(-1))/(1—x)2=(1—102x100+101x101)(1—x)2.
Подставлю x = 3.
Ответ: ≈ 2,078176333426855507665737416578*1050.
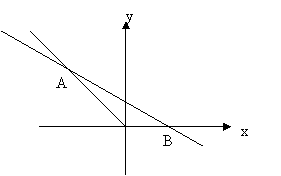
Задача 3. Найдите площадь треугольника AMB, если A и B — точки пересечения с осью OX касательных, проведенных к графику y = (9—x2)/6 из точки M(4;3).
Решение.
т. A = укас1∩OX Решение:
т. B = укас2∩OX укас =y(x0)+у’(x0)(x—x0);
y = (9—x2)/6 y’(x0) = -2x*1/6 = -x/3;
M(4;3)________ т.к. укас проходит через M(4;3), то
SAMB —? 3 = (9—x02) — (4—x0)* x0/3 | *3
18 = 9—x02—2x0(4—x0);
x02—8 x0—9 = 0;
Д/4 = 16 + 9;
x0 = 4+5 = 9;
x0 = 4—5 = -1
укас1 = -12 — (x—9)*9/3 = -3x+15;
укас1 = 4/3 + (x+1)*1/3 = x/3+5/3;
A(5;0); B(-5;0);
AM = √10 (ед.);
AB = 10 (ед.);
BM = 3√10 (ед.);
p — полупериметр; __
p = (4√10 + 10)/2 = 2√10 + 5;
__ __ __ __ __ __
S = √(2√10 + 5) (2√10 + 5—√10) (2√10 + 5—3√10) (2√10 + 5—10) =
= √(2√10 + 5)(√10 + 5)(5—3√10)(2√10—5) =
= √(40—25)(25—10) = 15 (ед2);
Ответ: 15 (ед2).
Задача 4. Какая наименьшая плоскость может быть у треугольника OAB, если его стороны OA и OB лежат на графике функции y = (|x|—x)/2, а прямая AB проходит через точку M(0;1).
Решение:
-x, x<0
y =
0, x>0
A(a;-a); B(b;0);_
AO = |a|√2 = -a√2 (т.к. a<0);
BO = b;
Для т. B:
у1 = kx +z;
т.к. у1—график линейной пропорциональности, проходящий через т M(0;1), то z = 1.
0=kx+1;
k=-1/b;
Для т. A:
у1=kx+1;
-a=kx+1;
k=(-1-1a)/a;
у1A= у1B
(-a—a)/a = -1/b;
b+ab=a;
a(1—b)=b;
a = b/(1-b);
S∆AOB=0,5*AO*OB*sin/_AOB
ÐAOB =180o—45o = 135o
S∆AOB=0,5*(√2/2)* (-a)b√2 = -ab/2;
S∆AOB = -b2/(2(1—b)) = b2/(2(1—b)); D(y): b>1(т.к. при b<1 не образует ∆AOB.);
т.к. функция непрерывна и дифференцируема на b>1, то найду ее производную:
S’ = (4b(b—1)—b2)/(4(b—1)2) = (4b2—4b—2b2)/(4(b—1)2) = 2b(b—2)/(4(b—1)2) =
= b(b—2)/(2(b—1)2);
S’ = 0;
точки экстремума:
b=0;
b=1;
b=2;
но b>1, значит
Sнаим =S(2) = 4/(2(2—1))=2(ед2);
Ответ: 2 ед2.
Задача 5. В прямоугольном параллелепипеде ABCDA1B1C1D1 с ребрами CD = 24, AD= 6 и DD1 =4 проведена плоскость через центр симметрии грани A1B1C1D1 , вершину А и точку Р, лежащую на ребре DC. Какую наименьшую площадь может иметь сечение параллелепипеда этой плоскостью? На какие части делит точка P ребро DC в этом случае?
Решение. Проведем плоскость и построим сечение (рис.). АО Î АA1C1С - линия, принадлежащая данной плоскости. Продолжим АО до пересечения с CC1 в точке S. Тогда SP - линия пересечения грани DD1C1C и данной плоскости, а сечение ANMP - параллелограмм. Sсеч = SAMNP = SK*AP/2 , потому что SK/2— высота параллелограмма ANMP. Это видно из следующего рассуждения.
В ΔASC ОC1 - средняя линия (значит SC1 = 4), в ΔPSC также средняя линия МC1, а плоскость A1B1C1D1 делит пополам любую линию между S и плоскостью ABCD, а значит и SK.
Пусть PC = x; ΔCLP подобен ΔDAP,
LC/AD = x/(24—x), LC = 6x/(24—x);_____________ ____________
Из ΔCLP: KC = (6x*x/(24—x))/(√(36x2/(24—x)2)+x2) = 6x/(√(36+ (24—x)2);
________ ___________________ __________________
Из ΔSCK: SK = √SC2+ KC2 = √64+36x2/(36+(24—x)2) = 2√16+9x2/(36+(24—x)2) ;
Из ΔADP: AP = √36+(24—x)2;_____ _________________ __________________
Sсеч = AP*SK/2 = 0,5*(√36+(24—x)2) 2√16+9x2/(36+(24—x)2) = √16(36+(24—x)2)+9x2;
Если S’(x) = 0, то 18x+16*2(24—x)(-1) = 0;
50x—32*24 = 0, x = 32*24/50 = 32*12/25 = 384/25 (это точка min);
Sсеч = 312;
DP = 24—16*24/25 = 216/25;
Ответ: 312 кв. ед.; DC: 384/25; 216/25.
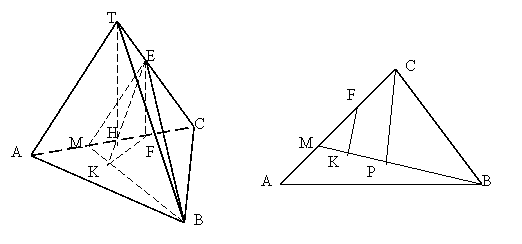Задача 6. Высота пирамиды TABC с основанием ABC проходит через середину ребра AC. Выберите на AC точку М так, чтобы площадь сечения пирамиды плоскостью, проходящей через точку M, середину ребра TC и вершину B, была наименьшей, если AB=BC=AC=TC=2.
Решение. HF=FC=1/2;
S∆BME = BM*EK*1/2;___ _
Из ∆TCH => TH = √4—1=√3;
EF = TH/2=√3/2;
Пусть MC = x.
Из ∆BMC по теореме косинусов MB2= x2+4—2*2*x*1/2;
MB = √x2—2x+4; _ _
S∆BMC = 0,5*MC*BC*sinC=(x/2)*2√3 /2 = x√3/2;
S∆BMC = 0,5*BM*PC, _ ________
PC = (2S∆BMC)/BM, PC = x√3/√x2—2x+4 ;
∆KMF подобен ∆PMC(по двум углам):
KF/PC = MF/MC(рис 2),_____ _ _________
KF = x√3(x—1/2)/(x√x2—2x+4) = √3(x—1/2)/(√x2—2x+4);
________ ______________________
Из ∆KEF => KE = √ KF2+EF2 = √3(x—1/2)2/(x2—2x+4)+3/4; _
S∆BME = 0,5√x2—2x+4 *√3(x—1/2)2/(x2—2x+4)+3/4 = 0,5√3(x—1/2)2+(x2—2x+4)*3/4;
Если S’(x) = 0, то
6(x—1/2)+(2x—2)*3/4 = 0;
15x—9 = 0;
x = 3/5; __
S(3/5) = √15/5 кв.ед.
Ответ: √15/5 кв.ед.
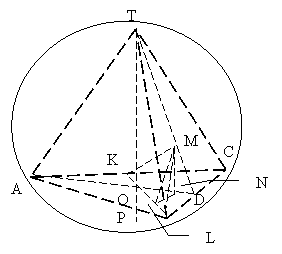
Задача 7. В сферу радиусом R вписана правильная треугольная пирамида, у которой боковое ребро образует с высотой пирамиды угол 60o. Какую наименьшую площадь может иметь треугольник MBK, если точка M лежит на апофеме пирамиды, а BK — высота основания пирамиды, не пересекающая апофему?
Решение. TP = 2R, ÐATO = 60o.
Пусть AB = BC = CA = a(рис.)
Тогда AO = a√3/3,
AD = BK = a√3/2, _ _
TO = AO*ctg60o= a√3/3*1/√3 = a/3,
OD = a√3 /6,
AO2 = TO*OP = TO(2R - TO),
a2/3 = a(2R – a/3)/3, a = 3R/2.
S∆MBK = BK*LM*1/2, BK = const,
S∆MBK = f(LM),__
LM = √MN2+NL2
Пусть MD = x, тогда MN = x cos / NMD; _
cos Ð NMD = TO/TD = a/(3√a2/9+a2/12 = 2/√7, MN = 2x/√7 .
Из ∆ONL: LN = ON cos30o (ÐONL = 30o);
ON = OD – ND, _ _ _ _ _
ND = x sin ÐNMD = x √3/√7, ON = a√3/6 - x√3/√7,
LN = (a√3/6 - x√3/7)√3/2 = (a/4 – 3x/(2√7)),
LM = √4x2/7+(a/4 – 3x/(2√7))2. _ _
Если LM’(x) = 0, то 8x/7+2(a/4 – 3x/(2√7))(-3/2√7) = 0,
8x/7 – 3a/4√7 + 9x/14 = 0,
25x/14 = 3a/4√7,
x = 21a/50√7. __ __
MN = (21a/50√7)*(2/√7) = 3a/25,
LN = a/4 – (3/2√7)*(21a/50√7) = 4a/25,
LM = √a2/625 + 9a2/625 = a√10/25. _
S∆MBK = a√3/2*a/5*1/2 = a√3/20 = 9√3 R2/80.
Ответ: 9√3 R2/80.
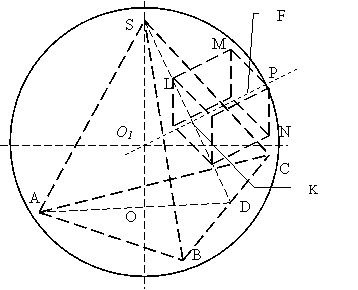
Задача 8. В сферу радиусом R вписана правильная треугольная пирамида, высота которой в 1,5 раза меньше высоты основания. Между боковой гранью пирамиды и сферой расположена правильная четырехугольная призма, одно из оснований которой (ближнее к центру сферы) лежит в плоскости боковой грани пирамиды, а вершины другого основания принадлежат сфере. Какой должна быть высота призмы, чтобы ее объем был наибольшим? Найти этот объем.
Решение. SABC – правильная треугольная пирамида (рис), вписанная в сферу радиусом R,
SO*1,5 = AD,
LMN – правильная четырехугольная призма.
Найти. Vпр = f(LM).
Пусть SO = H, тогда AD = 1,5H;
SO1 = R – радиус сферы; LM = x –высота призмы.
∆SKO1 подобен ∆SOD => O1K/OD = SO1/SD => OK1 = OD*SO1/SD.
Из ∆AO1O: R2 = AO2 + O1O2 = (2AD/3)2 + (AD*2/3 - R)2,
R2 = 4AD2/9 + 4AD2/9 –AD*R*4/3,
8AD2/9 = AD*R*4/3 => AD = 3R/2.
Отсюда OD = R/2;
AO1 = R и SO1 = R; _
SD = √R2 + R2/4 = R√5/2, _
OK1 = 2*R*R/(2R√5) = R√5/5;
O1K = R√5/5.
Из ∆O1FN => R2 = (O1K + x)2 + NF2,
 |
NF = √R2 – R2/5 – 2x(√5)2/5 – x2 ,
Sосн = 2NF2. _
Vпр = Sосн*x = 2(R2 – R2/5 – 2x√5 R/5 - x2)*x;
Vпр = 2(4R2x/5 – 2x2√5 R/5 - x3);
V’пр(x) = 2(4R2/5 – 2x√5 R/5 - 3x2) = 0; _
x 1,2 = (2R√5/5 + √4R2/5 + 12R2/5)/(-3) = (2R√5/5 + 4R/√5)/(-3);
x = 2√5 R/15 _ _
Vпр.max = 2(4R2*2√5R/(5*15) – 2√5R*4R2/(45*5) - _ 40√5R3/(225*15)) = 16R3√5(1 – 1/3 – 5/45)/75 = 16√5R3/135.
Ответ: 16√5R3/135 м3 при H = 2√5R/15.
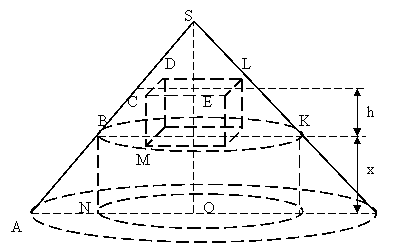Задача 9. В конус вписан цилиндр, одно из оснований которого лежит в плоскости основания конуса, а окружность другого основания принадлежит боковой поверхности конуса. Правильная четырехугольная призма расположена так, что ее нижнее основание лежит в плоскости верхнего основания цилиндра, вершины верхнего основания принадлежат боковой поверхности конуса. Отношение длины диагонали основания призмы к ее высоте равно отношению длины диаметра цилиндра к его высоте. При какой высоте цилиндра объем призмы будет наибольшим? Найти этот объем призмы, если высота конуса – H и радиус основания – R.
Дано. ASO – конус;
SO = H;
AO = R;
CL/CM = BK/BN;
Найти. BN, чтобы Vпр = max
Решение. BN = x, CM = h, Vпр = Sосн CM = CL2h/2.
∆CSD подобен ∆ASO: CD/AO = SD/SO;
CD/R = (H – x - h)/H;
CD = R(H – x -h)/H.
∆BSE подобен ∆ASO: BE/AO = SE/SO;
BE/R = (H - h)/H;
BE = R(H - h)/H.
Находим отношение CD/BE = (H – x - h)/(H - x).
Исходя из условия (CL/CM = BK/BN) задачи делаем вывод,
что CD/BE = h/x, т. е. (H – x - h)/(H - x) = h/x => h = (Hx – x2)/H
Тогда CD = R(H – x – (Hx – x2)/H)/H = R(H2 – Hx – Hx +x2)/H2 = R(H - x)2/H2,
CL = 2CD = 2R(H - x)2/H2.
V = 4R2(H - x)4(H - x)x/(2H*H4) = 2R2(H - x)5x/H5;
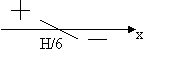V’(x) = 2R2((H - x)5 – 5(H - x)4 x)/H5 = 0,
(H – x) – 5x = 0, x = H/6.
V = 2HR2(5H/6)5/(6H5) = 2R2H*55/66.
Ответ: при H/6, Vmax = 2R2H*55/66.
В физике производная применяется в основном для вычисления наибольших или наименьших значений для каких-либо величин.
Задача 1.Потенциальная энергия U поля частицы, в котором находится другая, точно такая же частица имеет вид: U = a/r2 – b/r, где a и b — положительные постоянные, r — расстояние между частицами.
Найти:
а) значение r0 соответствующее равновесному положению частицы;
б) выяснить устойчиво ли это положение;
в) Fmax значение силы притяжения;
г) изобразить примерные графики зависимости U(r) и F(r).
U = a/r2 – b/r; Решение:
a и b — counts; Для определения r0 соответствующего равновесному
r0