Дискретизация и квантование изображений
ИСТОРИЧЕСКИЙ ОЧЕРК.
Еще с середины 40-ых годов , специалисты по радиоэлектроники начали задумываться над возможностью применения специализированных цифровых устройств для решения разнообразных задач ,связанных с обработкой сигналов . Нечего и говорить , что в то время выводы не были благоприятными . С точки зрения стоимости, размеров и надежности предпочтение следовало отдать аналоговой фильтрации и аналоговым методам спектрального анализа . В 50-ых годах теория управления , частично основанная на работе Гуревича ( 1945 г.) , уже утвердилась как самостоятельное научное направление ; были глубоко изучены принципы дискретизации колебаний и возникающие при этом спектральные эффекты , а математический аппарат теории z-преобразования , существовавший еще со времен Лапласа , начал находить применение в радиоэлектроники и смежных дисциплинах . Однако достигнутый уровень развития техники позволял получить практические результаты только в задачах управления медленными процессами и обработке низкочастотных сейсмических сигналов . К середине 60-ых годов были оценены потенциальные возможности интегральных микросхем , что позволило представить полную систему обработки сигналов , для которых наилучшая техническая реализация была бы именно цифровой .
Первый крупный вклад в теорию цифровой обработки сигналов , касающийся анализа и синтеза цифровых фильтров , был сделан Кайзером ( фирма Bell ) ; он показал , как можно рассчитывать цифровые фильтры с нужными характеристиками , используя билинейное преобразование . Примерно тогда же ( 1965 г.) появилась статья Кули и Тьюки о быстром методе вычисления дискретного преобразования Фурье , давшая мощный толчек развитию этого нового технического направления . Позже метод был развит и стал широко известен как быстрое преобразование Фурье ( БПФ ) . Ценность этого метода заключается в сокращении времени вычисления дискретного преобразования Фурье ( на один-два порядка для большинства практических задач ). Опубликование статьи Кули и Тьюки ускорило развитие строгой и достаточно полной теории цифровой фильтрации . Важнейшее значение метода БПФ состояло в том , что он наглядно продемонстрировал , насколько цифровые методы при спектральном анализе могут оказаться экономичнее аналоговых . После создания метода БПФ интенсивность исследований в области цифровой фильтрации резко возросла , и в настоящее время цифровые методы широко используются для спектрального анализа самых разнообразных сигналов , начиная с низкочастотных колебаний в сейсмологии и звуковых колебаний в гидрологии и при анализе речи и кончая видеосигналами в радиолокации .
Первой попыткой исчерпывающего изложения теории цифровой обработки сигналов была книга Гоулда и Рэйдера ( 1969 г.) . Эту книгу применяли в качестве учебного пособия для аспирантов, и как руководство для инженеров ,работающих в промышленности . Естественно , что книга не могла удовлетворить и тех и других . Не нужно доказывать , что хорошее учебное пособие может быть составленно только на основе курса , читавшегося в течении по крайней мере несколько лет , и подходящего набора задач .
ПРИЧИНЫ ВНЕДРЕНИЯ ЦОС В
ЭЛЕКТРОСВЯЗЬ.
1. Сложность ( нередко невозможность ) решения некоторых задач аналоговым методом .
2. Прогресс в развитии электроники ( создание высокоскоростных многоразрядных АЦП , разработка сигнальных процессоров ) .
3. ЦОС позволяет реализовать универсальные модемы , в которых изменением программы осуществляется переход с одного вида сигнала на другой ( т.е. с одной модуляции на другую ).
4. ЦОС позволяет строить адаптивные радиоприемные устройства, работающие во все усложняющейся электромагнитной обстановке ( т.е. спектр постоянно загружается сигналами ) .
5. Простота , автоматически сменных , алгоритмов ЦОС и высокая точность их реализации .
6. ЦОС позволяет реализовать более сложные алгоритмы радио приема ( разнесенный прием , компенсация и подавление сосредоточенных помех и прием в целом ) .
7. При использование ЦОС значительно меньше влияет разброс параметров и действие дестабилизирующих факторов.
8. Высокая интеграция цифровых микросхем позволяет реализовать очень сложные алгоритмы приема сигналов , сохраняя приемлемый объем и стоимость аппаратуры .
9. Цифровая аппаратура легко поддается миниатюризации. Высокая технологичность и отсутствие регулировки понижает стоимость.
10.Проектирование цифровых устройств легче чем аналоговых и поддается автоматизации ( легко модулируются на ЭВМ ) .
11.ЦОС облегчает работу по созданию спецэфектов на ТВ ( работа режиссеров на теле-студии ) .
12.ЦОС позволяет существенно повысить качество изображения.
ПРОБЛЕМЫ РАЗВИТИЯ ЦОС .
1. Для ЦОС необходимо преобразовать аналоговый сигнал в цифровой ( требуется достаточно большой уровень сигнала - порядка 1в ) .
2. Преобразование аналогово сигнала в цифровой приводит к появлению погрешности дискретизации во времени и к погрешности квантования по уровню ( специфические погрешности ) .
3. Процесс обработки сигналов сопровождается погрешностями , вызванными округлениями результатов ( это приводит к ошибкам - шумам ) .
4.Требуется увеличение динамического диапазона и ширины спектра преобразуемых аналоговых сигналов ( т.к. каналы с ограниченной полосой пропускания и сложной помеховой обстановкой ) . Чтобы достигнуть возможности аналоговой техники нужно иметь динамический диапазон АЦП 120-130 дб с df=100 кГц . Таких АЦП пока нет . Реализуемый при df=100 кГц динамический диапазон АЦП 70-80 дб . Для широкополосных сигналов при df=100 Мгц динамический диапазон 6-24 дб .
5. Низкая скорость работы цифровых вычислительных устройств. (Сигнальные процессоры : КМ1813ВЕ11 , ТМS320.10 , ТМS320.20 , ТМS320.30 , ДSР5600 , ТМS320.50 .)
ТЕОРЕМА КОТЕЛЬНИКОВА .
Любой сигнал с ограниченным спектром ( бесконечный во времени ) однозначно определяется своими отсчетами , взятыми через интервал времени dt=1/2F т.е.
, где u(kDt)-аналоговая величина;
Эта теорема утверждает , что если сигнал f(t) имеет преобразование Фурье Sf(w) отличное от нуля при частотах меньших 2pFm . То в отсчетах сигнала f(kDt) взятых через интервал Dt=1/2Fm содержится вся информация о непрерывной функции f(t) . Из теоремы следует , что эти отсчеты содержат информацию о сигнале f(t) в любой момент времени . Однако частота отсчетов должна быть по крайней мере в два раза больше высшей частоты сигнала Fm .
Доказательство.:
Дан сигнал f(t) , его спектр : S(w)=
при |w|<2pFm ,
0 , при |w|>2pFm.
Представим некоторую реализацию сигнала f(t) и его спектр S(f):
Если отсчеты сигнала брать с помощью бесконечно узких импульсов,расположенных в непосредственной близости друг от друга , мы однозначно определим любую функцию . Если интервал между импульсами увеличивать , то где-то мы начнем терять информацию о сигнале . Рассмотрим случай ,когда в качестве отсчетных импульсов используется периодическая последовательность импульсов длительностью t , повторяемых через Dt=1/2Fm . Временное и спектральное представление этих импульсов:
Спектр отсчетных импульсов можно записать в виде ряда Фурье , т.е.
yD(t)=A1coslt+A2coslt+A3coslt+............ Процедуру взятия отсчетов удобно рассматривать как умножение функции f(t) на функцию yD(t) . Результирующий дискретизованный сигнал можно представить в виде суммы последовательностей импульсов ,амплитуды которых равны значению функции f(t) в момент отсчета , а спектр такого сигнала представляет собой периодически повторяющуюся функцию Sf(w) с периодом l ,т.е.мы наблюдаем изменение амплитуды импульсов отсчета по закону f(t) и соответственно имеем амплитудную модуляцию каждой гармоники спектра импульсов отсчета сигналa :
Для восстановления првоначального сигнала нам достаточно отфильтровать полученный сигнал ФНЧ с частотой среза расположенной в интервале от Fm до 1/Dt-Fm . Рассмотрим какова может быть наименьшая частота следования счетных D импульсов, что бы еще имелась возможность отфильтровать полезный сигнал. В случае , если 1/D t=2Fm мы еще имеем возможность отфильтровать полезный сигнал если же 1/Dt<2Fm ,то произойдет наложение спектральных составляющих и восстановление первоначального сигнала без ошибки станет невозможным. Следовательно , для восстановления сигнала ,полученные отсчетные импульсы необходимо подать на вход ФНЧ с частотой среза равной Fm. Реакция идеального ФНЧ на узкий импульс единичной амплитуду представляет
собой функцию вида : y(t)=sin2pFt/2pFt
На вход фильтра мы подаем сумму импульсов с амплитудами равными f(kDt) Разложение сигнала f(t) в ряд Котельникова указывает на технический способ передачи непрерывной функции (сигнала) f(t)с ограниченным спектром путем передачи отсчетных импульсов ,который сводиться к следующему:
и со сдвигом один относительно другого на Dt=1/2Fm . Сигнал на выходе фильтра представляет собой сумму откликов ,т.е. 
Что соответствует ряду Котельникова .
Восстановление сигналов по его отсчетам .
1)взятие отсчета f(kDt) функции f(t) в моменты kDt ;
2)значение полученных отсчетов передаются на приемную сторону с использованием любогометода кодирования и модуляции ;
3)на приемной стороне вырабатываются короткие импульсы ,амплитуды которых пропорциональны принятым значениям отсчетов ;
4)полученные импульсы подаются на идеальный ФНЧ с частотой среза Fм . На выходе фильтра получается функция f '(t) , пропорциональная переданной функции f(t) . Идеальный ФНЧ с полосой пропускания Fм при действии на его вход единичного импульса d(t) дает на выходе напряжение ,соответствующее функции : y(t)=sin2p Fmt/2pFmt При восстановлении функции f(t) на вход фильтра подают короткие импульсы с амплитудами , соответствующими f(kDt) и с интервалами Dt. На выходе фильтра получается напряжение , соответствующее сумме откликов фильтра на каждый из импульсов . В моменты времени kDt функция f(t) восстанавливается совершенно точно , так как в этот момент только одна из отсчетных функций y(t-kDt) не равна нулю . В остальные моменты времени для точного восстановления необходимо суммировать бесконечное число отсчетных функций .
Ошибки восстановления сигнала по отсчетам Котельникова.
Как было отмечено выше , точное восстановление сигнала возможно только при строго ограниченном спектре сигнала и при использовании идеального ФНЧ .НА практике мы имеем дело с сигналами конечными во времени, т.е. бесконечным , теоретически , спектром и для восстановления используем реальные ФНЧ . Рассмотрим ошибки восстановления , вызванные реальностью сигнала (сигнал ограничен во времени , т.е. не ограничен по частоте ). Основная энергия сигнала сосредоточена в диапазоне частот до Fm и только малая доля будет выходить за Fm .
1)На основании т. Котельникова мы не можем восстановить спектральные составляющие , лежащие выше частоты Fm .
2)В спектре восстановленного сигнала появяться дополнительные составляющие , представляющие собой зеркальное отображение " вниз " по частоте спектральных составляющих сигнала относительно оси совпадающей с частотой среза идеального ФНЧ и равной Fm .Поясним
это на рисунке: фнч
S f(f) S1(f) S2(f) S3(f)
0 Fm 3Fm f
Огибающая спектральной плотности сигнала f(t) представляет собой функцию S1(f) . Спектр отсчетных импульсов SDf(f) представляет собой периодически повторяемую функцию S1(f) с периодом 2Fm . Идеальный ФНЧ с частотой среза Fm не пропускает составляющие основного сигнала и пропускает составляющие сектра амплитудно-модулируемой первой гармоники спектра отсчетных импульсов (2Fм) .
3)При восстановлении сигнала конечной длительности следует иметь ввиду что :
а) точность восстановления в средней части сигнала будет наибольшей, а по краям наименьшей;
б) в моменты , соответствующие отсчетам сигнал восстанавливается точно, а в средней части между отсчетными моментами ошибка максимальна
ВЫБОРКИ ИЗ АНАЛОГОВОГО СИГНАЛА.
Схема взятия выборки из аналогового сигнала.
1-Умножитель
2-Схема хранения УВХ
3-Квантователь
4-Преобразователь АЦП
5-Регистр
УВХ-устройство выборки и хранения. Перед умножителем стоит фильтр для уменьшения помех. Квантователь находит ближайший оцифрованный уровень. Устройство хранения дает время квантователю для принятия решения. Устройство хранения-конденсатор,окруженный ключами с большим сопротивлением ( т.е.RC-цепочкой с малой емкостью).Постоянная времени t стремится к единице, это переходный процесс в цепочке (т.е. конденсатор заряжается). За время Dt изменение сигнала мало,т.к. очень большое входное сопротивление преобразователя.Это и есть хранение. Преобразователь -преобразует вид кода (т.е. переводит его в бинарную систему счисления, за счет пороговых устройств). Регистр-считывает этот код, а за тем последовательно, побитно передает в линию.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ.
Квантование перидического сигнала.
W=2p/T
cosWT, cos2WT, ... , cosnWT.
n=3 n=Ґ
Много ли W нужно иметь и от чего это зависит (зависит от того насколько
гладкий сигнал).Если ширина спектра периодического сигнала конечно,
то он описывается конечным числом гармоник .N-кол-во отсчетов на один период.
ДПФ строго описывает периодический сигнал с конечным спектром ( если это не
соблюдается ,то появляется ошибка в представлении сигнала ДПФ ).
N-1
Cд(t)=е Ckd(t-kDt), где Т=NDt, Ck=C(kDt).
k=0
Ґ
т C(t)d(t-t)dt=C(t)-фильтрующее свойство d-функции.
-Ґ
Ґ
Cд(t)=е Cn*exp(j2npk/T) Пара преобразований Фурье
-Ґ
T
Cn=1/T тCд(t)exp(-j2npt/T)dt
0
NDt N-1
Сn=1/NDt т е Ckd(t-kDt)exp(-j2npt/T)dt={сжали ось времени symbol 120 \f "Symbol" \s 10xsymbol 61 \f "Symbol" \s 10=t/symbol 68 \f "Symbol" \s 10Dtsymbol 125 \f "Symbol" \s 10=
0 k=0
N N-1 N-1 N
=1/N т е Ckd(x-k)exp(-j2pnx/n)dx=1/N е Ck т d(x-k)exp(-j2npx/N)dx=
0 k=0 k=0 0
N-1
=1/N е Ckexp(-j2npk/N)
k=0
T=NDt
N-1
Cn=1/N е Ck exp(-j2npk/N) Пара дискретного преобразования Фурье
k=0
N-1
Ck= е Cn exp(jk2np/N)
0
Cn-комплексная гармоника, а N-кол-во отсчетов.
СВОЙСТВА ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ.
1. Линейность - если в цепи отклик на сумму воздействий равен сумме откликов.
Спектр суммы сигналов равен сумме спектров сигналов.
N-1
Ck= е Сxn exp(j2npk/N)
0 Выборки двух сигналов.
N-1
Uk= е Cyn exp(j2npk/N)
0
Zk=Ck+Uk , Линейность преобразования Фурье
Сzn=Cxn+Cyn ( для интегралов и сумм).
2. Для дискретного сигнала кол-во отсчетов спектра ( Сn) равно кол-ву
отсчетов сигнала.
3.Коэффициент (Со) дает постоянную составляющую.
N-1
Со=1/N е Ck ѕ это математическое ожидание.
k=0
4. Если N-четное ,то тогда
N-1 k
Cn/2=1/N е Ck(-1)
k=0
5. Если Ck - вещественные, то Cn ,расположенные симметрично
относительно Cn/2 образуют комплексно сопряженные пары.
N-1 N-1 +
C =1/N е Ck exp(-j2pk(N-n)/N)=1/N е Ck exp(j2kp/N)=Cn
N-n k=0 k=0
Отсчеты выше C повторяют спектр от Co до C .
N/2 N/2
Но мы не нарушаем теорему Котельникова, т.к. Сn комплексное число,
оно требует два числа для своего представления. Следовательно нужно
ровно N отсчетов ,как и по Котельникову ( N=2FT=T/Dt).
ЦАП и АЦП.
1 3 5
4
2 ЦАП АЦП 2
+5в +15в +5в
6 7 6
1.Стробирующий импульс ( аналоговая величина, соответствующая дис-
кретному слову).
2. N-разрядное дискретное слово (код).
3.Опорное аналоговое напряжение (определяет от какого сигнала ведется
счет т.е. служит для получения единиц измерения в дискретных долях).
4.Аналоговый сигнал.
5.Пуск (внешний сигнал - для конкретного момента времени будет получен
код).
6.Логическое питание.
7.Аналоговое питание.
Отдельные земли обеспечивают подавление импульсных помех ( т.е.возрастает
помехоустойчивость) по питанию.
Входные и выходные сигналы ЦАП и АЦП.
Сигналы ЦАП АЦП
аналоговый на выходе ; напряжение вход ; напряжение ; полярность ;
или ток ; полярность ; ве- величина ; ( есть однополярные
личина ( бывают одно- и двуполярные АЦП ) ;
и двуполярные ЦАП ) (2.5В , 5В , 10В , 10.24В , 20В)
(2.5В,5В,10В,10.24В,20В)
(1мА,1.2мА,1.5мА,2.5мА)
цифровое вход ; послед. или парал. выход ; последовательный
слово ( шина ) включение ; или параллельный ;
логические уровни :
ттл-5В ; эсл- -5В,-2.5В ;
кмоп-3В,15В ; источник
питания : анал.±15,±12В ;
дискр.+5В .
сигналы стробирующий импульс а) входной импульс начала
управления ( при завершении ввода преобразования.
слова , т.е. тактовый ввод) б) вых. “состояние”
( говорит , что на выходе
появился код )
Dt между сигналами а
и б - это врнмя , затрачи-
ваемое АЦП на преобра-
зование.
опорный эталонное напряжение , эталонное напряжение ;
относительно которого внешнее , внутреннее ;
ведется счет ; можно использавать перемен-
ное
При преобразовании мы можем получать прямой код Uвых. ( 0-10В ), или
двуполярный ( ± 10В ). При использовании ЦАП и АЦП необходимо обра-
тить внимание на используемый код ( т.к. они различны ).
Однополярные : как правило старший разряд обеспечивает 0,5 Uопор. ,
следующий разряд 0,25 Uопор. , ... , младший 1/ 2 Uопор. .
Двуполярные : первый разряд дает знак , следующий 0,5 Uопор. ,
n-1
младший 1/2 Uопор. .
-0,51 ё -0,38 ® 000 Декодирование аналогового
-0,38 ё -0,26 ® 001 напряжения в бинарное число
-0,26 ё -0,13 ® 010 DU = 0,128 - шаг квантования.
-0,13 ё 0 ® 011 Uразмаха = 1,024 В.
0 ё 0,13 ® 100 ( ошибка не больше 0,5 DU ).
0,13 ё 0,26 ® 101
0,26 ё 0,38 ® 110
0,38 ё 0,51 ® 111
ОСНОВНЫЕ ТИПЫ ЦАП.
1.Цепочка взвешенных резисторов.
R R Rвх.оу№0 ,Rключей№0 (удается реали-
зовать ключи с сопротивлением R»10 Ом)
2R Uвых~еIвх
4R Недостатки:
ОУ Слишком большой разброс сопротивлений
8R Uвых и как следствие трудность в изготовление
их на одной микросхеме .
Влияние Rвх.оу на цепь.
Uопорное
2.Цепочка R-2R .
+Uопорн
2R Uвых Достоинства:
Более технологична ,т.к.всего два
номинала сопротивлений.
-Uопорн 2R R Rн
2R R
2R R
2R
АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ.
А).АЦП последовательного приближения (скоростные).
xi(t) УВХ Ком- схема Umax
пар. управл Uвх
1/2Umax
ЦАП RG
Uвых Umin
цап n
вых 1 2 3 4 5
1.При подачи пускового импульса , после УВХ обнуляется регистр (RG),
затем в старший разряд регистра дается “1”,на выходе ЦАП появляется
напряжение равное 0.5Umax .Если Uвых.увх>Uвых.цап ,то ”1” в старшем
разряде остается ( иначе она стирается ).
2.Опять ставят “1” в следующий разряд регистра .......................................
.......................................................................................................................
Кол-во шагов соответствует кол-ву разрядов АЦП.
Б).АЦП параллельного действия .
Uопорн. В качестве опорного на каждый
компаратор (К) подается сетка
УВХ R напряжений - Uопорн.
xi(t) K n
2 n
R Kол-во компараторов = 2 .
K При подачи сигнала на вход АЦП ,
R ДЕКО- все компараторы у которых
K ДЕР Q2 Uопорн. дадут единици. R Q1 Наивысший номер компаратора K находящегося в единичном состоя- R Q0 нии соответствует выходному коду K АЦП. R Недостатки: K Эти АЦП малоразрядные (4-5) R (т.к.необходимо много компара- K торов). R K R КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ. x t)= x(t)+jh(t)=E(t)exp{ jy(t)} x(t) x ` ` h(t) пре- образ. При определенных правилах связи комплексное число дает аналитический сигнал ( т.е. непрерывный вместе со своими производными ) . E(t) Описание сигнала через огибающюю E(t) и фазу y(t) . y(t) 0 x(t) x(t)=Re{x(t)}=E(t)cosy(t) ` Нам нужно установить правило выбора сомножителей E(t) и cos(y(t)) т.к. если мы узнаем один , то легко найдем другой . Понятие огибающей очень расплывчато , поясним это на примерах : ( ) -огибающие для одного процесса разные . Первый дал понятие огибающей и фазе Гильберт , он дал определение мнимой составляющей ( т.е. ввел комплексные величины ) . Ґ (t)=1/p тxi(t )/ t-t dt Гильберта Ґ x(t)=1/p т h(t)/ t-t. dt -Ґ Преобразование Гильберта - широкополосный фазовращатель , оно поворачивает все спектральные составляющие на 90° . E(t)= Ц x(t) + h(t) - огибающая понятия применимые для любого сигнала . w(t)=dy(t) - частота на 90° ). x(t)= Acosw t +Asinw t = A Схема получения АМ ОБП .
h(t)
Пара преобразований -Ґ
ѕѕѕѕѕy(t)=arctg( (t)/ x(t)) - фаза
dt
x(t)=Acosw t ; h(t)=Asinw t ( т.е. h(t) получается приповороте x(t)
l 1/2cos(w -l)t+1/2cos(w +l )t
x(t) x(t)cosw t
генератор
cosw t
cos(w - l)t
+
j=p/2 j=p/2
sinlt sinw t h(t)sinw t
1\2cos(w - l)t- 1/2cos(w +l)t
+ Получили АМ ОБП без использования фильтров .
Мы оперируем комплексными функциями для того
чтобы убрать основную часть энергии несущей .
Огибающие и фаза УПСП (узко-полосного случайного процесса ).
Квадратурные составляющие огибающей .
Dw< 460 465 470 f,кГц y(t) = w0t- j(t) t t Фаза УПСП разбивается на две составляющие флуктуированную j(t) и мат.ожидания w0t . x(t) =Е(t)cosy(t)=E(t)cos(w0t -j(t))=E(t)cosj(t)cosw0t+E(t)sinj(t)sinw0t A(t) B(t) A(t) и B(t) медленно меняющиеся функции . Получаются , как случайные функции времени . x(t)=A(t)cosw0t + B(t)sinw0t , где A(t) и B(t) - квадратурные составляющие огибающей . В этом колебание вектор Е(t) будет колебаться , т.е. показывать флуктуацию. 4. Справедливо свойство ортогональности . ѕѕѕѕ ѕѕѕ h(t)x(t)=0 A(t)B(t)=0 5.-Ґ <=A(t) < Ґ ; -Ґ <=B(t)<Ґ;E(t)>=0 . ѕ ѕ 6. Если Гауссовский шум то A(t)=0 и B(t)=0 ( Т.е. нулевые мат. ожидания ) . Если A(t)=F то это значит что в случайном процессе x(t)=A(t)cosw0t + B(t)sinw0t+ Fcosw0t
w0 - ( ) j(t)
y(t)- ( )
A(t)
E(t)
j(t)
B(t)
Свойства функций :
1. Энергетические спектры G (w) иG (w) одинаковые .
2. Законы распределения одинаковые w (x)=w (x)=wa(x)=wб(x).3. Коррелляционные функции равны Bx(t )=B (t ) .появилась детерменированная ф-ия .
7. A (t)=B (t) =Gx - мощность реализации .
ѕ ѕ ѕ
E (t)= A (t)+B (t) =2Gx - мощность огибающей .
8. Ba(t)=Bб(t) ( т.к. скорости изменения одинаковы )
9. Bx(t)=Ba(t)cosw0t
ДИСКРЕТНАЯ СВЕРТКА.
Ґ
f(t)=тC(t)y(t-t)dt - Свертка -интеграл Дюамеля (прохождение
-Ґ сигнала через нелинейную инерционную
цепь)
N-1
fm=1/N* е CkUm-k - Свертка дискретных сигналов.
k=0 m=0,1,2,3,...,N-1.Т.к.число отсчетов описывающее
сигнал Х(t) ,будет описывать и функцию fn.
N-1
Ck=еСxn exp(j2pk/N) ;Cxn-амплитуда “n”-ой гармоники спектра.
n=0
N-1
Ym-k=е Cyl exp(j2pk/N)
l=0
N-1 N-1 N-1
fm=1/N е ( е Cxn exp(j2pk/N))( е Cyl exp(j2pl(m-k)/N))=
k=0 n=0 l=0
N-1 N-1 N-1
=1/N е е CxnCyl exp(j2plm/N) е exp(j2p(n-l)k/N)
n=0 l=0 k=0
N-1
При n=l , е exp(j2p(n-l)k/N)=N (Если n№l ,то сумма равна “0”).
k=0
Тогда получаем:
N-1
fm= е Cfn exp(j2pmn/N) ,где Cfn=CxnCyn
n=0
Если в одном из пространств пары преобразования Фурье мы
производим умножение ,то во втором пространстве будет про-
изводиться свертка .Это требуется для анализа длинной после-
довательности ,где легче перемножить спектры ,а потом взять
обратное преобразование Фурье .
Ck 2 2 2 Yk 3
2
1
 | | ||||||||
| |||||||||
 | |||||||||
 | |||||||||
| |||||||||
-1 0 1 2 -1 0 1 2
CmY(0-m) еXmY(1-m)
еXmY(2-m) еXmY(3-m)
еXmY(4-m)
fm
12
6
0 1 2 3 4 m
4.2.2. Дискретизация и квантование изображений
Сформированное и записанное изображение необходимо преобразовать в форму, пригодную для цифровой обработки. Если изображения записываются фотоэлектронным способом, то это обычно не составляет трудности, так как из сканирующего фотоэлемента поступает электрический ток, пригодный для дискретизации и квантования. Таким образом, данный случай можно рассматривать как распространение соответствующих методов цифровой обработки одномерных сигналов на двумерные сигналы. При этом ошибки квантования можно учесть введением в блок-схему дополнительного .источника шума (11). Расстояние между отсчетами должно удовлетворять теореме Найквиста для двумерных колебаний (1).
Устройства для дискретизации и квантования изображений основаны на технике микроденситометрии. В подобных системах на пленку проектируется луч света с интенсивностью I1. Интенсивность I2 света, прошедшего сквозь пленку (или отраженного от нее), измеряется фотоумножителем. По коэффициенту пропускания
Т=
(4.16)
с помощью соотношения (4.5) можно вычислить оптическую плотность. После этого световое пятно на пленке можно сместить скачком и таким образом получить отсчеты изображения. Математически этот процесс описывается соотношением
g1(x, y) =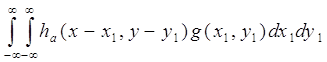
(4.17)
где g - изображение на пленке; ha распределение яркости в сечении луча, освещающего пленку; g1 эквивалентное изображение, из которого берутся отсчеты (т.е. в дискретных точках x = j
x, y = ky сканирующий фотоприемник измеряет именно g1). Матрица отсчетов g1 ( jx, ky ) представляет собой дискретизованное, или цифровое, изображение.
Из равенства (4.17) (справедливого также для случая дискретизации изображений, полученных фотоэлектронными средствами) видно, что в процессе дискретизации записанное изображение подвергается искажениям. За счет правильного выбора распределения ha и расстояния между отсчетами изображение можно фильтровать в процессе дискретизации. Фильтрацию, связанную с процессом дискретизации (согласно формуле (4.17)), можно использовать для подавления эффектов наложения, возникающих из-за того, что ширина спектра изображения обычно не ограничена (из-за шума зернистости пленки и других высокочастотных составляющих) (12). Дискретизация коэффициента пропускания эквивалентна дискретизации яркостного изображения, а дискретизация плотности эквивалентна дискретизации плотностного изображения. Часто можно услышать, что предпочтительнее квантовать плотность, так как логарифмическая зависимость приводит к уменьшению динамического диапазона. Однако подобные упрощенные рассуждения могут приводить к ошибкам (13).
4.2.3. Восстановление и демонстрация цифровых изображений
При цифровой обработке одномерных сигналов восстановление аналогового сигнала из последовательности чисел достигается путем низкочастотной фильтрации, что теоретически обосновывается теоремой об интерполяции колебаниями с ограниченным спектром (11). В идеальном случае для такой интерполяции следует применять функцию вида sin 
. Однако данная функция не имеет двумерного варианта, который можно было бы использовать для восстановления аналоговых изображений, так как импульсный отклик идеального фильтра нижних частот, имеющий вид sin
, принимает отрицательные значения, а это выдвигает требование получения отрицательного света, невыполнимое при восстановлении изображений.
Аналоговое изображение можно восстановить с помощью устройства, подобного примененному при дискретизации изображения. На чистую пленку проектируется луч света, а интенсивность этого записывающего луча модулируется в соответствии с числовыми значениями изображения. В качестве источника света, а также для непосредственной демонстрации изображений можно также применять электронно-лучевые трубки (ЭЛТ). Световое пятно перемещается по поверхности пленки согласно растровой сетке. Нетрудно увидеть, что процесс восстановления изображения описывается соотношением
g2(x, y) =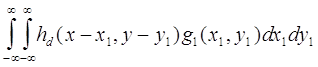
(4.18)
где hd- распределение яркости записывающего пятна, g1 - матрица отсчетов функции (4.17), представленная здесь набором взвешенных 
- импульсов, разнесенных на расстояния (x, y) друг от друга, а g2 - восстановленное непрерывное изображение. Распределение яркости записывающего пятна является импульсным откликом интерполирующего фильтра, аналогичного применяемому при восстановлении одномерных аналоговых сигналов. Практически во всех системах восстановления изображений записывающее пятно имеет несложное распределение яркости (например, гауссовское). По этой причине точно восстановить изображение не удается, поскольку простые распределения не дают возможности полностью подавить высокочастотные копии спектра изображения, возникающие при дискретизации. К счастью, обычно это не создает существенных трудностей, и в простых системах получается хорошее изображение.
Из вышеизложенного видно, что при дискретизации и демонстрации изображений возникают искажения спектра. Подобные искажения можно скорректировать в процессе цифровой фильтрации квантованных изображений (12).
Восстановление непрерывных изображений связано с другой проблемой, а именно с проблемой верности изображения. Если число, находящееся в памяти машины, представляет значение оптической плотности изображения в конкретной точке, то абсолютно верное воспроизведение получится, если пленка, предназначенная для демонстрации, будет иметь точно такую оптическую плотность, как записано в памяти ЭВМ. (Аналогичные требования можно сформулировать для коэффициента пропускания пленки я для характеристики фотоэлектронной системы ). Подобное устройство
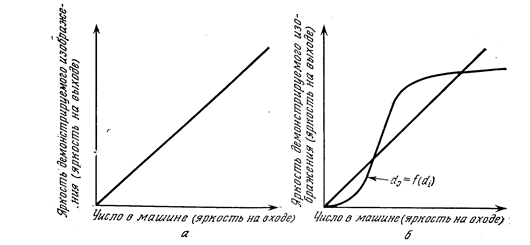
Рис. 4.4.
а - сквозные характеристики идеальной системы отображения; б - сквозные характеристики типичной реальной системы отображения.
отображения должно иметь сквозные характеристики» совпадающие с приведенными на рис. 4.4, а. Однако такие идеальные характеристики встречаются редко. Характеристики реальных устройств отображения больше напоминают приведенные на рис. 4.4, б, где наблюдается значительное отклонение от идеальной прямой с наклоном 45°. Хорошее приближение к идеальной характеристике можно получить путем линеаризации характеристики устройства отображения. Для этого необходимо выполнить следующие действия:
1. Сформировать набор фиксированных значений коэффициента пропускания или оптической плотности, подать их на устройство отображения и измерить фактический его отклик на каждое из значений коэффициента пропускания или оптической плотности.
2. Измерения, полученные на этапе 1, задают характеристику устройства отображения d0 = f ( di). Линеаризованная характеристика описывается соотношением di= f- -1( d0 ). Это обратное преобразование можно найти эмпирическим путем и представить в виде таблицы или полинома, вычисленного методом наименьших квадратов.
3. Перед демонстрацией изображения числовые данные следует преобразовать согласно функции f -1. В результате в них будут введены предыскажения и значения яркостей, записанные в машине, будут воспроизведены на экране без погрешностей.
Метод линеаризации характеристик устройств отображения успешно применялся во многих исследовательских институтах. Точная линеаризация, конечно, невозможна, так как форма нелинейной характеристики изменяется в зависимости от особенностей проявления пленки, чистоты химикатов, старения (или повреждения) люминофора ЭЛТ и т.п. Однако, приложив определенные усилия, можно линеаризировать устройство отображения так, что отклонения от линейности не будут превышать ±5% максимального значения. Следует отметить, что линеаризация характеристики устройства отображения является операцией, применяемой при восстановлении аналоговых изображений; при обработке одномерных сигналов линейными электронными схемами она обычно не используется.
4.2.4. Свойства системы зрения человека
Очень часто окончательную оценку изображения делает человек. Если бы человеческое зрение было идеальным и отвечало на световое воздействие с абсолютной точностью и совершенной линейностью, то его можно было бы и не изучать. Однако система зрения человека обладает нелинейной характеристикой, а ее отклик не является абсолютно верным. Важность этих положений .для получения изображений признана довольно давно (13), однако они не в полной мере использовались при обработке изображений.
Одной из характеристик системы зрения человека является способность восприятия яркости света. Эксперименты по определению восприятия людьми минимально различимых градаций яркости света, поступающего от калиброванного источника, показали, что яркость света воспринимается глазом нелинейно. Если начертить график зависимости величины этой минимально различимой градации яркости от эталонной яркости, то при изменении яркости в пределах нескольких порядком этот график имеет логарифмический характер (14). Такие субъективные экспериментальные результаты согласуются с объективными данными, полученными в экспериментах на животных, в которых было показано, что светочувствительные клетки сетчатки и оптический нерв возбуждаются с частотой, пропорциональной логарифму интенсивности подводимого к ним света (15). По вполне понятным причинам подобные объективные измерения на людях не проводились. Тем не менее объективные данные для животных и субъективные показания для людей более чем убедительно подтверждают вывод о том, что яркость света
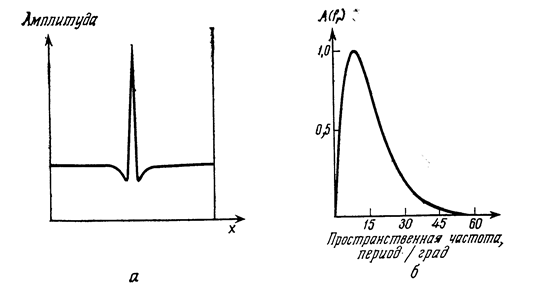
Рис. 4.5.
a- сечение (осеcимметричной) аппаратной функции глаза человека; б - сечение (осесимметричной) частотной характеристики глаза человека.
воспринимается по логарифмическому закону. Это существенно нелинейный закон.
Другой отличительн