Расчёт поперечно-строгального станка
Содержание
1. Структурный анализ
1.1.1. Исходные данные 1
1.1.2. Определение недостающих размеров 1
1.1.3. Структурный анализ механизма 1
1.2. Графический метод исследования механизма 2
1.3. Графоаналитический метод исследования механизма 4
1.4. Построение годографа центра тяжести кулисы 6
1.5. Построение аналога угловой скорости и аналога ускорения кулисы 7
1.6. Расчёт погрешности 7
1.7. Аналитический метод расчёта 7
2. Силовой расчёт механизма
2.1. Исходные данные 10
2.2. Определение сил инерции звеньев 10
2.3. Определение реакций в кинематических парах 10
2.3.1. Структурная группа 10
2.3.2. Структурная группа 11
2.3.3. Силовой расчёт ведущего звена 11
2.4. Определение уравновешивающей силы при помощи рычага Жуковского 11
2.5. Определение мощности электро привода 12
3. Проектирование кулачкового механизма
3.1. Исходные данные 13
3.2. Построение графика движения 13
3.3. Определение минимального радиуса кулачка 13
3.4. Построение профиля кулачка 13
3.5. Построение графиков углов передачи движения 14
4. Проектирование зубчатой передачи
4.1. Исходные данные 16
4.2. Расчёт редуктора 16
4.3. Построение картины зубчатого зацепления 17
4.4. Зацепление с инструментальной рейкой без смещения 18
4.5. Зацепление с инструментальной рейкой со смещением 19
5. Расчёт маховика
5.1. Исходные данные 20
5.2. Построение графика приведённого момента сил полезного сопротивления 21
5.3. Построение графика работ 22
5.4. Построение графика изменения кинетической энергии машины 23
5.5. Построение графика изменения кинетической энергии звеньев машины 23
5.6. Определение момента инерции маховика 24
5.7. Конструирование маховика 24
5.8. Расчёт привода 25
Список использованной литературы 26
1. Структурно-кинематический анализ.
1.1.1 Исходные данные.
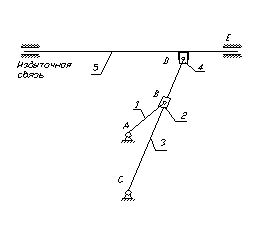
Рис. 1 Кинематическая схема долбёжного станка.
Исходные данные: Lва=140 мм. Lcd=710 мм. Lac=430 мм. Lcs3=290 мм. h=315 мм. Lcs3=0.29 м.
1.1.2 Определение недостающих размеров.
Определим угол q - между крайними положениями кулисы. Для этого рассмотрим прямоугольный треугольник АВоС, где <АВоС=90°, т.к. в крайних положениях кулиса является касательной к окружности радиусом Lab с центром в точке А.
Sin(q/2)=Lab/Lac=140/430=0.3256
q/2=arcsin0.3256=19°q=19°х2=38°
Таким образом, коэффициент скорости хода:

К=Vхх/Vрх= =1,5
1.1.3.Структурный анализ механизма.
Подвижность механизма: W=3n-2p5-p4=3*5-8*2-0=-1
Кинематическая пара Е’ введена для того, чтобы звено 5 не работало на изгиб и не влияет на характер движения механизма. Подвижность механизма без учёта Е’ W=3*5-2*7=1.
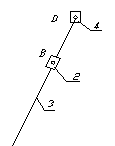 Разложим механизм на структурные группы
Разложим механизм на структурные группы
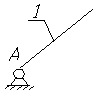
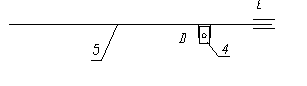
n=2 P5=3 W=3х2-2х3=0
Формула структурного строения механизма.
Механизм класса 2-го порядка
1.2 Графический метод исследования механизма.
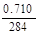
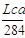 Масштаб длины ml= = =0.0025 м/мм.
Масштаб длины ml= = =0.0025 м/мм.
Пересчитаем длины звеньев в соответствии с новым масштабом
АВ= = =56 мм. СD= =284 мм. AC= =172 мм.
Cs3= =116 мм. h= =126 мм.
Для определения перемещения ведомого звена вычертим схему механизма в 12 положениях, образованных поворотом кривошипа на 30°. За начальное положение выбираем начало рабочего хода Во. Вычертим также дополнительное положение конец рабочего хода Во’- в положение 8’.
Таким образом, первому положению соответствует j=0 и S=0, второму положению j=30°, а S – это разница между проекциями точки D на направление ЕЕ. Таким образом, каждому положению кривошипа соответствует определённое перемещение и путь звена. На основании этого строим график пути – перемещения ведомого звена. Для построения выбираем следующие масштабы:
Масштаб перемещения ms= = =0,005 м/мм.
Последовательно дважды графически дифференцируя полученный график зависимости S=f(j) получим график аналога скорости и ускорения
=f(j) = f(j)
Возьмем базу дифференцирования графика H1=28мм.
Масштаб угла поворота mj= = =0,052 рад/мм.
Масштаб скорости mv= = =0,00343 м/смм.
База дифференцирования графика скорости 7,5 мм.
Масштаб ускорения mа= = =0,0088.
Угловая скорость w= = =15,7 рад/с. (для ведущего звена)
Для того чтобы из графиков аналога скорости и аналога ускорения ведомого звена получить истинное значение скорости необходимо взять высоту соответствующего графика в мм умножить на соответствующий масштаб и угловую скорость w ведущего звена.
Максимальный угол отклонения кулисы:
L/L=sin a a=arcsin(56/172)=19°
Максимальное перемещение рабочего звена:
S=187*0.005=0.93 м.
Табл.1
Модули перемещения, скорости и ускорения выходного звена.
№ положения | Перемещения | Скорость | Ускорения | |||
| Мм. черт. | М. | Мм. черт | М/с | Мм. черт | М/с2 | |
1 2 3 4 5 6 7 8 9 10 11 12 | 0 12,5 36 70 117 141 169 184 177 134 70 16 | 0 0,0625 0,18 0,35 0,585 0,705 0,845 0,92 0,885 0,67 0,35 0,08 | 0 28 45 48,5 48 43 32 13 35,5 83 88 31 | 0 1,5 2,4 2,6 2,5 2,3 1,7 0,7 1,9 4,46 4,7 1,7 | 25 15 8 1,5 1 5 10 16,5 30 19 13 42 | 54 32,5 17,3 3,3 2,2 10,8 21,7 35,8 65 41 28,2 91 |
Пример расчёта скорости и ускорения для некоторых положений
Для 3 положения
V=Vмм*mv*w=45*0.00343*15.7=2.4 м/с.
a=aмм.*ma*w*w=8*0.0088*15.7*15.7=17.3 м/с2
1.3. Графоаналитический метод исследования механизма.
В графоаналитическом методе задача о скоростях и ускорениях решается построением планов скоростей и ускорений.
1.3.1. Построение плана скоростей.
Рассмотрим порядок построения плана скоростей для данного механизма.
Угловая скорость вращения кривошипа АВ:
wав=pi*n/30=5pi 1/c.
Скорость точки В1 – конца кривошипа:
Vb1=wав*Lав=0,7pi м/с.
Вектор Vв1 направлен перпендикулярно АВ в сторону вращение кривошипа АВ.
Для построения планов скоростей выбираем масштаб mv=0,05 м/смм.
Составляем векторные уравнения для определения скоростей характерных точек. Точка В3 характеризует положение кулисного камня и принадлежит кулисе CD. Движение точки В3 можно рассмотреть как движение вместе с концом кривошипа (точка В1) и движение относительно него, а также как движение относительно неподвижной точки С. На основании этого составим векторные уравнения:
![]()
![]()
![]()
![]()
![]()
![]()
![]() Vb3=Vb1+Vb3b1,
Vb3=Vb1+Vb3b1,
Vb3=Vc+Vb3c.
![]()
При этом нам известно: у Vb1 – величина и направление, у Vb3b1 – направление (параллельно CD), у Vb3c – направление, а Vc=0.
Построив вектор Vb3, определяем скорости точек D1 (конца кулисы) и S3 (цент тяжести кулисы) из пропорции. Направление движения всех этих трёх точек одинаково, а величину находим из пропорции:
= и =
Точка D3 принадлежит звену 5, следовательно, её скорость по величине и направлению совпадает со скоростью ведомого звена. Находим её по следующему векторному уравнению:
Vd5Ех=Vd4+Vd5d4 , где Vd3 направлена горизонтально, Vd3d1 направлена вертикально.
Для определения величины скорости из плана скоростей необходимо длину отрезка характеризующего эту скорость (в мм.) умножить на масштаб mv.
1.3.2. Построение плана ускорений.
Рассмотрим порядок построения плана ускорений для данного механизма.
аВ1 = аВ1 = wАВ*L АВ = 3.5pi2 м/с2
аВ1 направлено параллельно АВ от конца кривошипа к центру его вращения.
Для построения плана ускорений выбираем масштаб:
mа=1 м/мм.с2
Составим векторные уравнения для определения ускорений характерных точек для диады
![]() ab3=ac+anb3c+atb3c ,
ab3=ac+anb3c+atb3c ,
ab3= anb1+аkb3b1+аrb3b1 ac=0
ab3c= V2b3c/Lb3c, ab3c параллельно CD и направлено от D к C.
ab3c перпендикулярно CD.
аb3b1=2*wCD* Vb3b1 и направлено паралельно CD
wСD= Vb3c./Lb3c
Величину Аd4 определяем аналогично Vd4, составив векторные уравнения для диады
![]() Ae=Aex+Aeex
Ae=Aex+Aeex
Ae=Ad4+Aed4 Aeex=Ad4+Aed4
Величина ускорения находится из плана ускорений перемножением длины отрезка характеризующего данное ускорение на mа.
Приведём пример определения скоростей и ускорений графоаналитическим методом для 4 положения механизма.
Определяем Vb3:
![]()
![]()
![]()
![]()
![]()
![]()
![]() Vb3=Vb1+Vb3b1,
Vb3=Vb1+Vb3b1,
Vb3=Vc+Vb3c.
Для данного положения механизма Vb3b1 – направлено параллельно CD от D к C, а Vb3c перпендикулярно CD и направлена в сторону вращения кулисы. Выполнив построение, получим длину отрезка, характеризующего величину Vb3 nb3=43 мм., а длина CB=263 мм. Длины отрезков nd1 и hc находим как:
![]()
nd1= * nb3=53 мм.
![]() ns3= * nb3=37 мм.
ns3= * nb3=37 мм.
Построим эти отрезки на плане скоростей в направлении, совпадающем с направлением Vb3.
Vd3=Vd1+Vd3d1 , где Vd3 направлена горизонтально, Vd3d1 направлена вертикально.
Подсчитаем величины скоростей по формуле:
Vi=Ni*mv
nb3b1=12 мм. VB3B1=0.6 м/с.
nb3= 43 мм. VB3=2.14 м/с.
nd1=55 мм. Vd1=2.7 м/с.
nd3=54 мм. Vd3=2.67 м/с.
nd3d1= 4.4 мм. VD3D1=0.22 м/с.
Модули скоростей, вычисленные графоаналитически
Табл2
№ положения | Vb3b1 | Vb3 | Vs3 | Vd1 | Vd3d1 | Vd3 |
М/с | ||||||
1 | 2,2 | 0 | 0 | 0 | 0 | 0 |
2 | 2,01 | 0,94 | 06 | 1,41 | 0,31 | 1,38 |
3 | 1,2 | 1,85 | 1,04 | 2,51 | 0,46 | 2,47 |
4 | 0,534 | 2,14 | 1,1 | 2,7 | 0,22 | 2,67 |
5 | 0,28 | 2,2 | 1,1 | 2,73 | 0,19 | 2,72 |
6 | 1,07 | 1,92 | 1,05 | 2,48 | 0,39 | 2,45 |
7 | 1,77 | 1,26 | 0,72 | 1,79 | 0,57 | 1,7 |
8 | 2,2 | 0,22 | 0,19 | 0,38 | 0,13 | 0,35 |
8’ | 2,2 | 0 | 0 | 0 | 0 | 0 |
9 | 2,105 | 0,69 | 0,51 | 1,38 | 0,41 | 1,3 |
10 | 1,19 | 1,885 | 1,73 | 4,4 | 1,19 | 4,21 |
11 | 0,64 | 2,105 | 2,07 | 5,12 | 0,44 | 5,09 |
12 | 1,76 | 1,32 | 0,97 | 2,8 | 0,57 | 2,73 |
Построение плана ускорений.
Определяем Ad3
![]() Ad3=Ab1+Ab3b1=Ab3b1
Ad3=Ab1+Ab3b1=Ab3b1
Ad3=Ac+Ab3c+Ab3c
Для данного положения Ab1 направлено параллельно АВ от В к Аb3b1=2wcd*Vb3b1=2*4*1.25=10 м/с2, где wcd=Vd4/Lcd=2.85/0.71=4 рад/с
Vb3b1=1,25 м/с скорость камня относительно кулисы
Ab3c=Vb3c2/La3c=1.752/(212*0.005)=2.9 м/с2.
Anb1=w2*Lab=15.72*0.14=34.5 м/с2.
Ad4=Ab1*Lcd/Lb3c=12*284/210=16.2 м/с2.
1.4. Построение годографа центра тяжести кулисы.
Скорость центра тяжести кулисы определим из плана скоростей
Vц=Lpd4*mv*Lcs3/CD
Выберем масштаб скорости годографа mvц=0,05 м/с.мм.
Vц2=33*0,05*0,29/0,71=0,67 м/с. Lvц2=0,67/0,05=13,4 мм.
Длины векторов годографа
Табл. 4
№ п.п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Lpd4 | 0 | 33 | 46 | 55 | 56,5 | 49 | 37 | 10 | 35 | 100 | 105 | 55 |
Lvc | 0 | 13,4 | 18,8 | 22,5 | 22,6 | 20 | 15 | 4 | 14,3 | 40,8 | 43 | 22,5 |
1.5. Построение аналога угловой скорости и аналога углового ускорения кулисы.
Угловую скорость кулисы определяем из плана скоростей:
wк2=Lpd42*m/CD=33*0.05/0.71=2.3 рад/с
Выберем масштаб для аналога угловой скорости mw=0,1 рад/с.мм.
Аналог углового ускорения кулисы построим графическим дифференцированием графика аналога угловой скорости.
База дифференцирования Hw=6 мм. таким образом
me=mw/(mj*H)=0.1/(0.052*6)=0.32 рад/с2мм.
Для 8 положения e8=Le8*me=12*0.32=3.8 рад/с2.
1.6. Расчёт погрешности.
Вычислим среднюю погрешность при определении скорости рабочего органа методом планов скоростей и графическим методом
Еv3=(Vпс-Vг)/Vпс=45*0,05-2,4/(45*0,05)=5%
Еv5=(155*0.05-2.5)/55*0.05=9%
Ev10=(90*0,05-4,46)/(90*0,05)=1%
Есрv=(Ev3+Ev5+Ev10)/3=5%
Вычислим погрешность при определении ускорений:
Еа=(Апс-Аг)/Апс
Еа1=(57-54)/57=5%
Еа3=(17-17,3)/17=1%
Еа10=(63-57)/63=9%
Есра=(Еа1+Еа3+Еа10)/3=5%
Таким образом, погрешности находятся в допустимых пределах.
1.7. Аналитический метод расчёта.
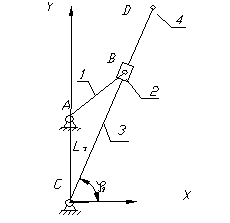 |
Составим уравнение замкнутого векторного контура АВСА
L1+L4=L3 (1)
В проекции на оси неподвижной системы координат X Y:
![]() L1cos(j1)=L3cos(j3)
L1cos(j1)=L3cos(j3)
L1sin(j1)+L4=L3sin(j3) (2)
XL1=L1cos(j1)
YB1=L1sin(j1)+L4
Угол поворота кулисы ВС
j3=Arctg(L1sin(j1)+L4/(L1*cos(j1)) (3)
![]() Положение камня кулиса 2
Положение камня кулиса 2
L3=L1 (4)
Координаты точки D:
Xd=Lcd*cos(j1) Yd=Lcdsin(j3) (5)
Угловая скорость кулисы
w3=L1cos(j1-j3)* w1/L3 (6)
Скорости точек звеньев:
Xb1=-L1w1sin(j1) Yb1=L1*w1cos(j1) Vb1=L1*w1. (7)
Xd=-Lcdw3sin(j3) Yd=-Lcdw3cos(j3) (8)
Vb3b1=-L1w1sin(j1-j3) (9)
Xb3=-Lcb3w3sin(j3) Yb3=-Lcb3w3cos(j3) Vb3=Lcb3w3 (10)
Угловое ускорение кулисы
E3=Lb3cw21sin(j1-j3)/L1-2Vb3b2w3/L3 (10)
Ускорение точек звена
Xb1=-L1w21cos(j1), Yb1= -L1w21sin(j1) Ab1=L1*w12. (11)
Xd=-Lcd*E3sin(j3)-Lcdw23cos(j3)
Yd=-Lcd*E3cos(j3)-Lcdw23sin(j3) (12)
![]()
Ad=
Рассмотрим пример
![]() j1=109° j3=Arctg(L1sin(j1)+L4/(L1*cos(j1))=94°,6
j1=109° j3=Arctg(L1sin(j1)+L4/(L1*cos(j1))=94°,6
L3=L1 =0,564 м.
w3=2,198cos(j1-j3)/L3=3,775 1/с
Vb3b1=-2,198sin(j1-j3)=-0,545 м/с
Vd=Lcdw3=0.71w3=2.68 м/с
E3=-34,545sin(j1-j3)+2Vb3b2w3/L3=-7,9
Xd=-0,71*E3sin(j3)-Lcdw23cos(j3)=6,408 м2/с
Yd=0,71*E3cos(j3)-Lcdw23sin(j3)=-9,632 м2/с
![]() Ad= =11,569 м2/с.
Ad= =11,569 м2/с.
Аналогичным образом, пользуясь выражениями (8), (9), (11), (13), (14), (15), найдем значения скоростей и ускорений для всех положений механизма. Результаты представлены в виде таблицы 5.
Табл.5
Ускорения и скорости, вычисленные аналитически.
№ пол. | j1° | j3° | L3, м | w3 1/с | Vb1b3, м/с | Vd, м/с | Ес 1/с2 | Ad, м/с2 |
1 | 199 | 109 | 0,407 | 0 | -2,2 | 0 | -84,88 | 60,26 |
2 | 169 | 106 | 0,477 | 2,15 | -1,95 | 1,53 | -46,5 | 33,22 |
3 | 139 | 101,4 | 0,532 | 3,27 | -1,34 | 2,33 | -23,07 | 18,07 |
4 | 109 | 94,6 | 0,564 | 3,77 | -0,5 | 2,68 | -7,9 | 11,57 |
5 | 79 | 87,3 | 0,568 | 3,82 | 0,32 | 2,72 | 4,5 | 10,8 |
6 | 49 | 80,2 | 0,543 | 3,46 | 1,14 | 2,46 | 18,47 | 15,63 |
7 | 19 | 74,4 | 0,494 | 2,52 | 1,81 | 1,8 | 39,09 | 28,12 |
8 | -11 | 71,1 | 0,426 | 0,7 | 2,18 | 0,5 | 73,15 | 51,94 |
8’ | -19 | 71 | 0,407 | 0 | 2,2 | 0 | 84,87 | 60,26 |
9 | -41 | 72,6 | 0,354 | -2,5 | 2,01 | -1,77 | 117,7 | 83,70 |
10 | -71 | 81,3 | 0,301 | -6,4 | 1,02 | -4,6 | 97,2 | 75,17 |
11 | -101 | 95,2 | 0,294 | -7,8 | -0,61 | -5,1 | -62,8 | 57,68 |
12 | -131 | 105,8 | 0,337 | -3,5 | -1,84 | -2,53 | -124,76 | 89,04 |
2. Силовой расчёт.
2.1. Исходные данные:
Усилие резани Рпс=130 кг.
Веса звеньев G1=10 кг G2=2 кг. G3=16 кг. G4=2 кг. G5= 22 кг.
Угловая скорость кривошипа:
w1=15,7 рад /с.
Длины звеньев:
Lcd=0.71 м. Lас=0,43 м. Lab=0.14 м. Lcs3=0.29 м.
Для 3 положения механизма имеем:
As5=17 м/с.
As3=(Ab3/Lcb3)Lcs3=(12/214)*117=6.6 м/с2.
e3=(Ab3/(Lcb3*mv))=12/(214*0.0025)=22.4 рад/с2.
2.2. Определение сил инерции звеньев.
Из механики известно, что любую систему сил можно привести к главному вектору сил:
Р=ma;
И главному моменту инерции:
Mи=-Ise
Действующих относительно точки приведения, за которую мы принимаем центр масс звеньев.
Определим Ри и Ми для всех звеньев механизма:
Ми5=0 т.к. w=0 Ри5=G5*A5/g=22*17/10=37.4 кг.
Ми4=0 т.к. J4=0 Ри4=G4*A4/g=2*17/10=3.4 кг.
Ми3=J3*E3=0.04*22.4=0.896 рад/с2. Ри3=22,4*0,29*16/10=10 кг.
Ми2=0 т.к. J2=0 Ри2=w21Lab=15.72*0.14=34.5 кг.
Точкой приложения Ри3 служит точка S3. За точку приложения Ри5 условно принимаем середину между опорами Е.
После определения сил инерции звеньев и точек их приложения проводим дальнейшие расчёты для каждой группы отдельно.
2.3. Определение реакций в кинематических парах.
2.3.1. Структурная группа
силовой расчёт начнём с наиболее удалённого звена т.к. все силы действующие на него известны. Действие отброшенных звеньев и реакций опор заменяем силами R0-5 и R3-4. Определим их величины и направления. Масштаб построения выберем mp=1 кгс/мм.
Рассмотрим равновесие звена 5:
ΣРi=0 G5+Pи5+Рпс+ R0-5 + R4-5=0
У реакции и сил, подчеркнутых одной чертой известно направление, двумя чертами величина и направление. Реакция R0-5 – направлена вертикально; R3-4- горизонтально. Построением силового многоугольника определим их величины (действием сил трения пренебрегаем).
Далее рассмотрим равновесие звена 4:
ΣРi=0 R5-4 + Ри4 +G4 +R3-4= 0
R4-5=-R5-4 Построением находим величину и направление R3-4, которая приложена к шарниру. Для нахождения точки приложения R0-5 составим уравнения моментов всех сил, действующих на данную структурную группу относительно точки D.
ΣМd=0
РИ5*h1+R0-5h+Pпс(Pпс –0.01)=0
H=(37.4*18*0.0025+130(18*0.0025-0.01))/22=0.238 м.
2.3.2. Структурная группа
В точке D приложим силу P4-3=-P3-4 . Звенья 1 и 2 соединены вращательной кинематической парой, значит, реакция P1-2 приложена в шарнире В. Звенья 3 и 2 образуют поступательную кинематическую пару, а так как силой трения мы пренебрегаем, то реакция между ними направлена перпендикулярна CD.
Рассмотрим равновесие кулисы (звена 3).
Составим уравнение моментов относительно точки С:
ΣМс=0 R4-3 h3 +PИ3 h3 +G3 h3 +Mи-P2-3h=0
R2-3=(170*150+10*0.6+16*9+0.896)/113=227 кг.
Для определения реакции Rс-3 составим уравнение суммы всех сил действующих на звено 3. Точка приложения силы – шарнир С
ΣFi=0 R4-3 +RИ3 +G3 +R2-3 +Rс-3=0
Для определения её величины и направления строим силовой многоугольник
LRс-3=26 мм. RС-3= LR0-3 mR=26*2=52 кг.
Для определения реакции R1-2 действующей со стороны ведущего звена на кулисный камень рассмотрим равновесие звена 2 (кулисного камня).
ΣFi=0 РИ2 +G3 +R3-2 +R1-2=0 R3-2 = -R2-3.
Для определения её величины и направления строим силовой многоугольник
LR1-2=119 мм. R1-2= LR0-3 mR=119*2=238 кг.
2.3.3. Силовой расчёт ведущего звена.
Ведущее звено представляет собой зубчатое колесо, выполненное с кривошипом, как одно целое. Ведущее звено будем считать статически и динамически уравновешенным, следовательно, Ри=0. Так как оно вращается с постоянной угловой скоростью то Е=0 þ Ми=0, число зубьев z=100. Модуль зубьев шестерни ведущего звена m=14.
На ведущее звено действуют силы: G1 – сила тяжести =10 кг. R2-1=-R1-2=238 кг. RА-1 – сила, действующая со стороны стойки на ведущее звено. Для того чтобы механизм совершал заданное движение необходимо к ведущему звену приложить уравновешивающую силу Рур. Точка её приложения – точка касания окружностей делительных окружностей зубчатых колёс ведущего звена и выходного колеса редуктора и составляет 20°(угол зацепления) к касательной, проведённой в этой точке.
Для нахождения Рур рассмотрим равновесие звена 1. Составим уравнение моментов относительно точки А.
ΣМа=0 R2-1 h1’ +Pур h1 =0
h1=(mzcos20)/2=(14*10*cos20)/2=285.7 мм.
h1’=Lh1*ml=13.5*10=135 мм.
Рур=R2-1*h1’/h1=238*135/285.7=112
Для определения Ra-1 составим следующее уравнение
ΣF=0 R2-1 + RA-1+ G1+Pур=0
Точкой её приложения служит шарнир А. Для определения велечины и направления построим силовой многоугольник.
Lа-1=
2.4. Определение уравновешивающей силы с помощью рычага Жуковского.
Повернём план скоростей на 90° по часовой стрелки для данного положения. Все внешние силы, включая силы инерции и веса звеньев, переносим параллельно себе в соответствующие точки плана и добавляем Ми3. Скорость точки F – приложения силы равна:
Vf=mz*w1/2=14*100*0.001*15.7/2=11 м/с.
Данный план скоростей и сил можно рассматривать как жесткий рычаг. Для определения Рyр составим уравнения моментов относительно точки Р, где плечом будет служить, длинна перпендикуляра, опущенного из полюса до линии действия силы
-(Рпс+Ри5+Ри4)*190-G4*19-Pи3*53-Ми3w3-G3*12-G2*69+Pур*11/0,025*cosa=0
Рур=((130+13,7+3,4)*190+2*19+10*53+0,896*15,7+16*12+2*69)/(440*cos20)=109 кг.
Найдём погрешность определения Рур различными способами.
Δ=(Рур ж-Рур пс)/Рур ж=(112-109)/112=3%
2.5. Рассчитаем необходимую мощность привода
М=РgV/m,
Где Р – уравновешивающая сила, V – скорость точки её приложения (11 м/с), m -- КПД привода
М=112*9.8*11/0.8=15 кВт.
3. Проектирование кулачкового механизма.
3.1. Исходные данные
Закон перемещения коромысла + - К
jу=113,6°=1,9827 рад.
jдс=14,2°=0,2478 рад.
jп=109°=1,9024 рад.
jбс=123,2°=2,15 рад.
Lкор=0,12 м.
βmax=25°=0,4363 рад.
γmin=60°
3.2. Построение графиков движения
Выразим перемещение в линейных единицах. Тогда линейное перемещение конца коромысла
Smax=Lкорβmax=0.12*0.4363=0.05236 м.
Аналог ускорения в первой половине фазы удаления величина постоянная и положительная, а во второй постоянная и отрицательная. Причём по модулю эти величины равны, тогда:
d2S/dj2=4Smax/j2у=4*0.05236/1.98272=0.053278 м.
Таким образом, на фазе удаления аналог ускорения принимает значения +-0,053278м.
На фазе удаления ускорение изменяется аналогично
d2S/dj2=4Smax/j2п=4*0.05236/1.90242=0.0579 м.
Таким образом, на фазе приближения аналог ускорения принимает значения +-0,0579м.
График аналога скорости на фазах удаления и приближения имеет вид равнобедренного треугольника, но с тем различием, что на фазе удаления dS/dj>0, а на фазе приближения – dS/dj<0.
Высоты этих треугольников определим по формулам:
На фазе удаления dS/dj=2Smax/jy=2*0.05236/1.9827=0.0528 м.
На фазе приближения dS/dj= -2*Smin/jп= -2*0,05236/1,9024= -0,055 м.
График перемещения на фазе удаления имеет вид двух сопряженных парабол, вершина одной из них находится в начале координат, другой в точке с координатами (jу, Smax/2). Построение ведут следующим образом. Из середины отрезка jу восстанавливают перпендикуляр и на нём откладывают отрезок Smax, затем делят этот отрезок на 12 частей. Отрезок, соответствующий jу также делим на 12 частей. Затем из начала координат проводят лучи через точки 1-6, а из точки с координатами (jу, Smax) – лучи через точки 6-12. Каждый луч, пересекаясь с одноимённой ординатой, проведённой через деления отрезка соответствующего угла удаления jу, даёт точку, принадлежащую параболе. Далее соединяем эти точки плавной кривой.
График перемещения на фазе приближения строится аналогично.
3.3. Определение минимального радиуса кулачка.
Для определения минимального радиуса кулачка Rmin строим совмещенный график. Для этого из произвольно взятой точки О’ радиусом равным ВоО’=Lкор/ml проводим дугу. Соединяем произвольно взятую на этой дуге точку Во с точкой О’ прямой линией.
Далее от точки Во по дуге радиуса R=BoO’ откладываем с графика перемещения соответствующие отрезки S=Lкор*β, где Lкор берётся в масштабе ms=ml. Полученные точки 0-25 представляют собой положение центра ролика коромысла, соответствующие заданным угла поворота кулачка.
Для определения центра О вращения кулачка на лучах О, 0’1,O’2,…,O’25 отложить отрезки dS/dj в масштабе mv=ms. При этом отрезки dS/djy откладываются по соответствующим лучам от дуги радиуса ВоО’ в направлении О’, т.к. в эту сторону направлен dS/dj. А отрезки dS/djп на фазе приближения откладываются от дуги радиуса ВоО’ в направлении противоположном О’.
В результате получаем точки Во, В1,…,В25. Через эти точки проведём прямые под углом γmin к соответствующим лучам. Поле ограниченное этими прямыми может рассматриваться как область возможных центров вращения кулачка, т.к. для любой точки этой области будет выполнятся условие, что во время работы кулачка угол передачи γ на всех фазах не будет меньше γmin. Расстояние ОBо даёт величину Rmin, в масштабе ms=ml, а расстояние ОО’ – межцентровое расстояние.
По данным совмещенного графика
Rmin=45*ms=45*0,000873=40 мм.
3.4. построение профиля кулачка.
3.4.1 построение теоретического профиля кулачка.
Из произвольной точки О проводим окружность радиуса ОО’. Масштаб построения профиля возьмем ml=0.000873 м/мм.
На этой окружности из произвольно взятой на ней точке Оо’ в сторону противоположную вращению кулачка (-w) откладываем фазовые углы – получаем точки О’12, O’13 и O’25. Затем делим jу и jп на 12 частей, как и на графике перемещения. Получаем точки Оо’,O’1,…,O’25. Из точки О радиусом Rmin проводим окружность, а из точки Оо’ радиусом равным длине коромысла АоОо’ проводим дугу, на которой откладываем дуговой путь согласно графику перемещения. Полученные точки дают положение коромысла при повороте кулачка на соответствующий угол. Обозначим эти точки как Ао,1,2,…,25. Из точки О как из центра, проводим окружности через эти точки. Из точек О1’,O2’,…,O25’ циркулем делаем засечки на соответствующих окружностях радиусом АоОо’. Полученные таким образом точки принадлежат теоретическому профилю кулачка. Обозначим их А1, А2,…,А25. Соединив их плавной кривой, получим теоретический профиль кулачка.
5.4.2 Построение профиля практического профиля кулачка.
Для уменьшения износа профиля кулачка и потерь на трение коромысло необходимо снабдить роликом. Размер ролика выбирают из условия выполнения закона движения, чтобы не получить заострения практического профиля кулачка, т.е. rp<0,8рmin, и из условия конструктивности rp<0,4 Rmin, где Rmin – минимальный радиус профиля кулачка, р. – минимальный радиус кривизны профиля кулачка на выпуклой части. Окончательно радиус ролика берётся меньший из двух вычислений.
Так как в данном случае pmin совпадает c Rmin, то окончательно радиус ролика вычислим по формуле:
rp= 0,4 Rmin = 0.4*45 =18 мм.
для вычерчивания практического профиля нужно провести ряд окружностей радиусом ролика с центрами на теоретическом профиле в точках Ао,…,А25. Проведя далее огибающую этих окружностей получим линию эквидистантную теоретическому профилю кулачка, т.е. отстоящую от него на равные расстояния – радиус ролика, который и будет являться практическим профилем кулачка.
3.5. Построение графика углов передачи движения.
График изменения угла передачи движения γ по углу поворота кулачка строим по данным полученным графическим способом. Для этого точки Во,…,В25, полученные на совмещенном графике соединим с центром вращения кулачка О. Тогда острые углы, образованные этими прямыми с соответственными лучами, дают искомые углы γ.
Табл 7.
Углы передачи, измеренные графическим способом.
| № пол. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| γ° | 75 | 70 | 65 | 63 | 62 | 62 | 64 | 72 | 80 | 87 | 92 | 97 | 79 |
| № пол. | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| γ° | 79 | 75 | 72 | 70 | 68 | 65 | 62 | 68 | 74 | 81 | 89 | 97 | 100 |
Выберем следующие масштабы для построения графка mj=0.18271 рад/мм. mγ=1°/мм.
Как видно из таблицы минимальный угол передачи больше минимально допустимого, следователь заклинивания в механизме не произойдёт как на прямом ходе, так и при реверсе.
4. Проектирование зубчатой передачи.
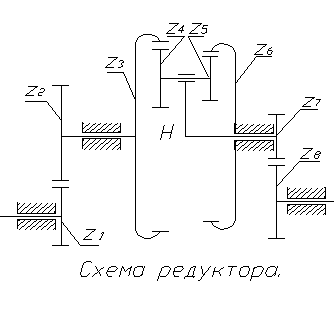
4.1. Исходные данные для проектирования зубчатой передачи:
Модуль m=14 мм.
Zш=13
Zк=30
aинструмента=20°
С=0,25m=3,5 мм.
ha=1
число зубьев колёс редуктора
z3=106
z4=48
z5=18
z6=76
z7=25
z8=100
n1=1400 об/мин
n8=150 об/мин
4.2. Расчёт редуктора.
Напишем уравнение передаточного отношения редуктора:
U1-8 = I1-2*I3-H*I7-8 = n1/n8 =1400/150 = 9.33
I3-6=(w6-wH)/(w 3-wH)=Z4Z6/(Z3Z5)
I3-H=n3/nh=1-i36.
I3-6=I34*I56=(-1)Z4/Z3(-1)Z6/Z5=(Z4Z6)/(Z3Z5)
I3-H=1-(48*76)/106*18=1-304/159= -0.912
I7-8=(-1)Z8/Z7=-N7/N8= -100/25= -4
N7=NH= -I7-8*N8=4*150=600 об/мин.
N=IN= -0.912*600= -547.17 об/мин.
N3=N2,
I1-2= (-1)Z2/Z1= -N1/N2= -2.5586.
Z2/Z1= 2.5586
Наиболее близко этому значению соответствует Z2=74 и Z1=29.
Рассчитаем число оборотов сателлита по формуле Виллиса:
I5-6=(w5-wH)/(w6-wH)=Z6/Z5, т.к w6=0, то
1-w5/wH=Z6/Z5
N5=N4=(1- Z6/Z5)NH=(1-76/18)*600= -1933.3 об/мин.
4.3. Построение картины зубчатого зацепления.
Применяем неравносмещенное зацепление. Из справочных таблиц имеем:
Iш-к= Zк/Zш= 30/13=2,3
Δy=0.18 X1=0.8 X2=0.471
XΣ=X1+X2=1.271
Y= XΣ –ΔY=1.091
Определим угол зацепления aw:
Inv aw=2*(X1+X2)/(Zш+Zк)*tga +inva=
2*1.271*tg20°/43+0.014904=0.036421.
Отсюда a w =26°34’45’’
Рассчитаем размеры зубчатых колёс по следующим формулам:
Шаг зацепления: Рa=р*m=43,9мм.
Радиусы делительных окружностей:
R1=mZш/2=91 мм; R2=mZk/2=210 мм.
Радиусы основных окружностей
Rb1=R1cosa w =81.38; Rb2=R2cosa w =187.8
Толщина зуба по делительной окружности:
S1=Pa/2+2*X1*m*tga=30.15
S2= Pa/2+2*X2*m*tga=26.73
Радиусы окружностей впадин:
Rf1=R1-m(ha+c-X1)=84.7
Rf2=R-m(ha+c-X2)=199.1
Межосевое расстояние
aw=m((Zш+Zk)/2+Y)=316.274
Радиусы начальных окружностей
Rw1=R1(1+2Y/(Zш+Zк))=95,6177
Rw1=R2(1+2Y/(Zш+Zк))=220,6563
Глубина захода зубьев:
Hd=(2ha-Δy)m=25.48
Высота зуба: h=hd+cm=28.98
Радиусы окружностей вершин:
Ra1=Rf1+h=113.68
Ra2=Rf2+h=228.074
Для построения выбираем масштаб ml=0,001 м/мм.
Построение картины зацепления начинаем с дуг начальных окружностей, касающихся в точки Р – полюсе зацепления. Через точку Р проводим прямую NN, образующую угол aw с общей касательной ТТ к начальным окружностям в точке Р. затем из центров О1 и О2 зубчатых колёс опускаем на прямую NN перпендикуляры О1N1 и O2N2, являющиеся радиусами основных окружностей rb1 и rb2, и строим основные окружности. Строим эвольвенты, которые описывает точка Р прямой NN при перекатывания её по основным окружностям, как для первого, так и для второго колеса. Проводим окружности впадин и вершин колёс. Проводим делительную окружность первого колеса. От точки С пересечения этой окружности с соответствующей эвольвентой откладываем по делительной окружности вправо и влево дуги СК и СЕ, равные шагу зацепления Рa в масштабе. Затем от точек Е, С и К откладываем влево дуги ЕF, CD и KL, равные толщине зуба S1. На втором колесе построения аналогичны.
Переходим к определению активной линии зацепления. Теоретической линией зацепления является отрезок N1N2 прямой NN. Активной линией зацепления является отрезок В1В2 прямой NN, заключенный между точками её пересечения с окружностями вершин колёс.
Определяем дугу зацепления. Для этого через крайние точки В1’ и B2’ рабочего участка профиля зуба первого колеса проводим нормали к этому профилю, то есть касательные к основной окружности первого колеса. Дуга а1в1 начальной окружности, заключенная между точками а1 и b1 пересечения этих нормали с начальной окружностью, является дугой зацепления первого колеса. Дугу зацепления а2b2 для второго колеса находим аналогично. Подсчитаем длину дуг зацепления:
A1B1=В1В2/(сosaw)=48/(cos26°34’45’’)=54.3 мм.
Подсчитаем коэффициент перекрытия по формуле:
Ea=В1В2/(p*m*сosaw)=48/(14*p*cos26°34’45’’)=1.22
При этом отрезок В1В2