Теоретическая механика (шпаргалка)
Статика:
Уравновешенные силы:
Система сил, под действием которой свободное твердое тело может находится в покое, называется уравновешенной.
Аксиомы статики:
а)Аксиома о уравновешенных силах (о абсолютном твердом теле) - две одинаковые силы, приложенные к абс. твердому телу и действуют вдоль одной прямой в противоположных направлениях назыв. уравновешенными силами. б) Аксиома о прибавлении или вычитании уравновешенной системы сил - действие системы сил на твердое тело не меняется, если если прибавить к ней уравновешенные силы. в) Аксиома сложения сил - силы, которые действуют на точку, можно складывать как векторы или аналитично. г)Аксиома о опорах (связи) и их реакции - силы могут быть активными и пассивными. Первые стремятся вызвать ускорение матер. точек. Другие - ограничивают движение. Они возникают как реакции системы на движение или на действие активных сил. Движение матер. точек может быть свободным или ограниченным. Во втором случае тело или точка назыв. несвободной. Все, что ограничивает движение тел в пространстве называется опорой (связью). д)Аксиома о освобождении от связи (опоры) - механическое состояние системы материальных точек не изменится, если освободить ее от связей, меняя их силами, действие которых такое же, как и связей (опор). Эти силы назыв. реакциями связей - пассивные силы, которые направлены в противоположную сторону относительно ограничения движения.
Момент силы относительно точки.
Вращательный эффект силы характеризуется ее эффектом. Моментом силы относительно центра О называется величина, равная взятому с соотв. знаком произведению модуля силы на длину плеча.
Момент силы относительно оси.
Моментом силы относительно оси называется скалярная величина, равная моменту проэкции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.
Пара сил, момент пары. Свойства пар сил.
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абс. твердое тело. Моментом пары наз. величина, равная взятому с соотв. знаком произведению модуля одной из сил пары на ее плечо (Понятие момента силы связано с точкой, относительно к-рой берется момент. Момент пары определяется только ее моментом и плечом; ни с какой точкой плоскости эта величина не связана). Св-ва : сумма моментов сил пары относительно точки не зависит от выбора точки и всегда равняется моменту пары, Пара сил не имеет равнодействующей - нельзя уравновесить одной силой.
Сложение пар сил.
Система пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же плоскости и имеющей момент, равный алгебраической сумме моментов слагаемых пар.
Теорема Вариньона.
О моменте равнодействующей - момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.
Виды нагрузок.
а) Сосредоточенная, б) Рассредоточенная равномерная и неравномерная, в) Пара сил - момент.
Параллельный перенос сил. Приведение системы сил к одному центру.
Силу можно переносить в любую точку тела, к-рая называется точкой приведения, если прибавить при этом пару сил (в точку приведения).
Главный вектор и главный момент произвольной системы сил.
Все силы, которые действуют на тело можно привести к одной точке, при этом вместо сил имеем эквивалентную систему сил, которая состоит из главного вектора и главного момента (пара сил). Частные случаи приведения произвольной системы сил к одному центру - а) главный момент равен равнодействующей, если главный момент М=0, б) Fгол=0, Мгол<>0, в) Fгол<>0, Мгол<>0, Мгол перпендик. Fгол - плоская система сил. г) Мгол<>0 Fгол<>0 Мгол || Fгол - силовой винт. е) Fгол=0, Мгол=0 - равновесие тела.
Условия равновесия произвольной пространственной системы сил.
S - сумма, Мгол = S Мi(F) = 0; Fгол = S Fi = 0;
Написать проекции на все оси.
Условия равновесия произвольной плоской системы сил.
а)Одной проекции силы нет, зато есть один момент с индексом этой оси б) есть два момента - нет двух сил в) Все моменты равны нулю.
Формы условий равновесия. ??????
Центр параллельных сил - это точка приложения равнодействующей системы параллельных сил.
Центр тяжести однородного тела.
Центр тяжести плоской фигуры.
Трение скольжения, угол трения.
Закон Кулона-Амонтона - F=fN. Угол трения - это угол, тангенс к-рого равен коэффициенту трения - предельный угол силы к нормали пов-ти, чтобы тело поехало.
Кинематика:
Теоремы о скоростях.
а) Проекции скоростей (абсол. твердого тела) двух точек на прямую, которая проходит через них равны. б) Скорость любой точки складывается из скорости какой-либо другой точки, принятой за полюс, и скорости ее вращения вокруг этой точки.
Мгновенный центр скоростей. Связь скоростей точек с мгновенными радиусами при п.п.д.
МЦС - это точка в плоскости движения, скорость к-рой в данный момент времени равна нулю.
Способы определения мгновенного центра скоростей.
Всего - четыре.
Динамика точкии системы:
Основное уравнение динамики для свободной и несвободной материальной точки в векторной, координатной и естественной формах.
Д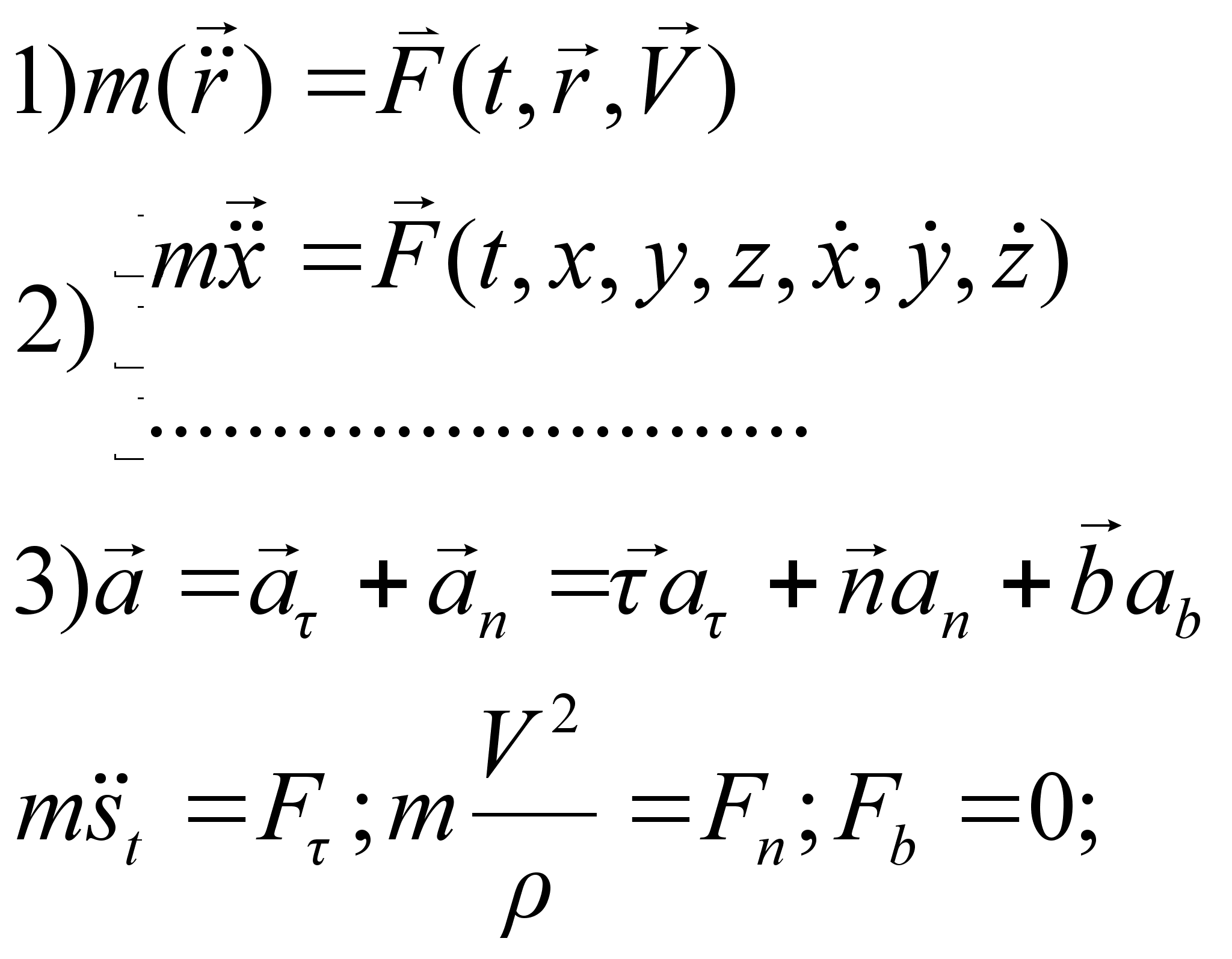
ля несвободной точки – к силе прибавляется вектор N – реакция опоры.
Теорема – о независимом действии сил – если на точку действует несколько сил или равнодействующая то точка будет двигаться с ускорением = сумме ускорений, к-рые возникают при действии каждой силы отдельно.
Вывести и сформулировать принцип Даламбера для точки.
ma = F + N; F + N + (-ma) = 0; Ф = -ma; - сила инерции.
Решение второй задачи динамики точки.
Это - зная силы найти закон движения. а) Показываем начальное и конечное положение тела. б) Направляем ось х из начального в конечное положение, ось у – перпендикулярно х с начального положения, в) Показываем тело в свободном положении и действующие на него силы, г) составляем дифур движения точки в проекции на ось х, д) интегрируем это уравнение, е) находим постоянные интегрирования с начальных условий и неизвестные величины. That all.
Две основные меры механического движения точки.
Импульс (кол-во движения) и кинетическая энергия.
Р![]()
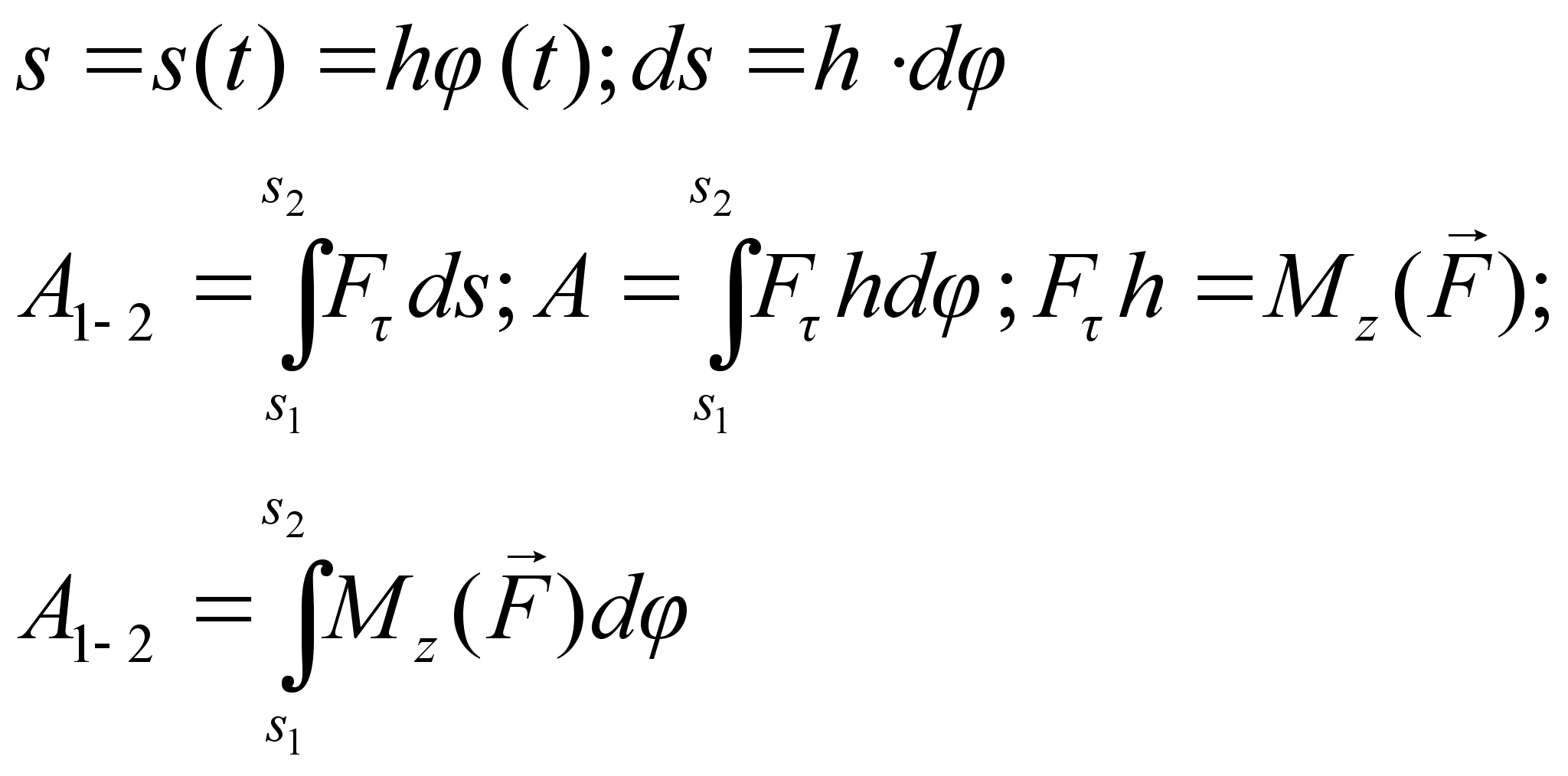
абота упругой силы. - Частный случай
Работа силы, когда тело вращается.
Теорема об изменении кинетической энергии точки.
Изменение кинетической энергии точки при некотором ее перемещении равно сумме работ внешних сил, которые действуют на этом перемещении на точку.
Д![]()
иф. уравнение движения мех системы и св-во внутренних сил.
Т
еорема об изменении кинетической энергии системы.
Идеальные связи – сумма возможных работ реакций которых равна нулю.
Возможные перемещения, возможная работа силы.
Возможное перемещение – это бесконечно малые перемещения точек мех. системы, которые мы представляем и которые разрешены связями. Возможные работы находятся по таким же правилам как и действительные, но вместо дифференциалов записываются их вариации.
Принцип Лагранжа-Даламбера (Общее уравнение динамики)
Н![]()
еобходимыми и достаточными условиями действительного движения мех. системы на к-рую действуют голономные двусторонние стационарные и идеальные связи есть равенство нулю суммы возможных работ всех активных сил и сил инерции на любых возможных перемещениях системы.
Связи, классификация связей.
а) геометрические (без производных), б) кинематические (дифференциальные r’=V), в) интегрируемые (это кинемат. К-рые можно привести к геометрич. r=s), г) односторонние, д) двухсторонние, е) нестационарные –f(t).
Принцип возможных перемещений.
Необходимыми и достаточными условиями для равновесия мех. системы, к которой приложены двусторонние, стационарные и идеальные связи, есть равенство нулю суммы возможных работ всех активных сил на любых возможных перемещениях из положения равновесия.
Обобщенные координаты, скорости, силы.
Н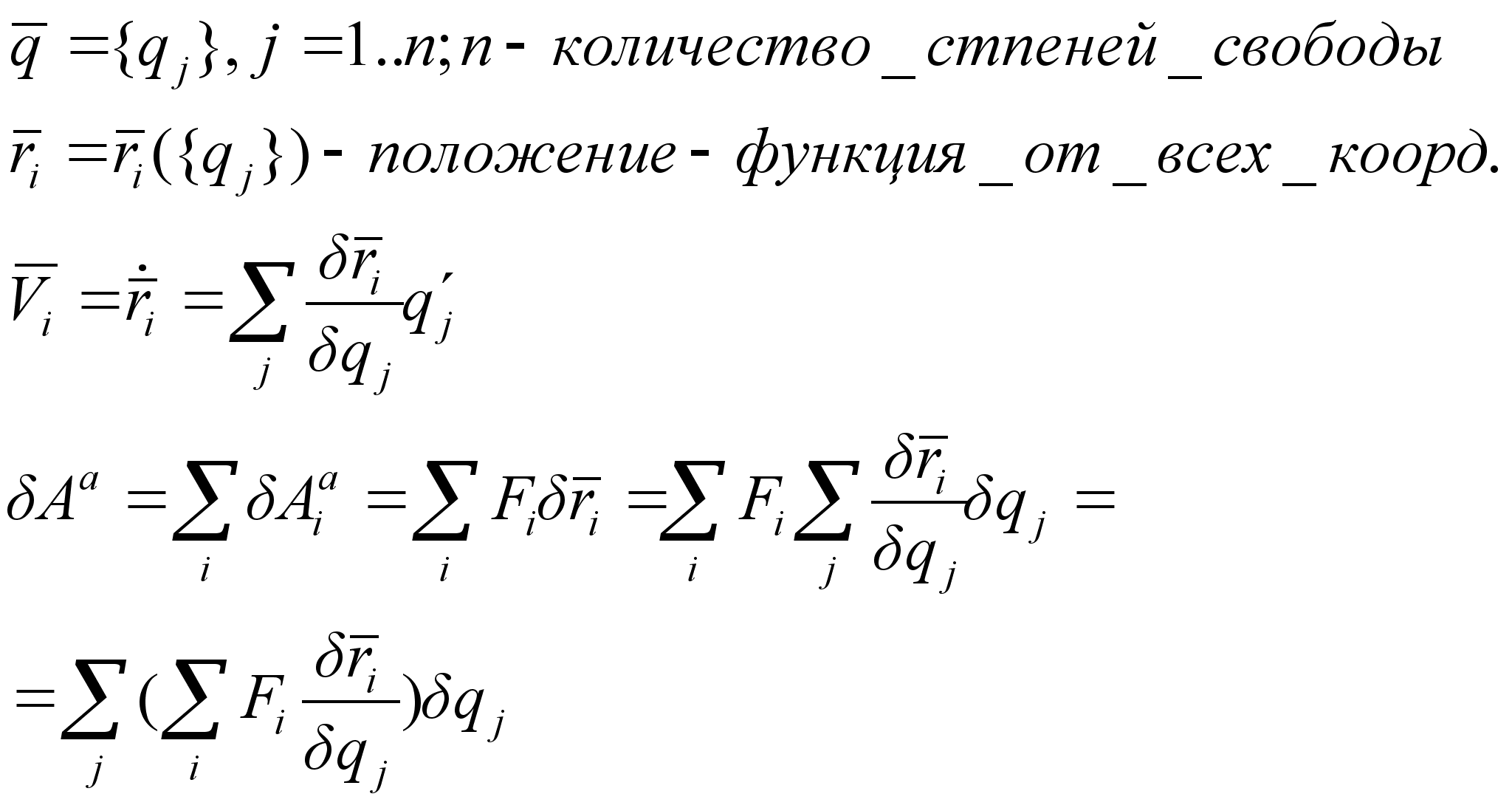
азываются независимые параметры, которые однозначно определяют положение мех. системы (эти параметры – любой размерности).
Обобщенная сила – это коэффициент при вариации обобщенной координаты в выражении возможной работы.
Обобщенная сила инерции.
![]()
Уравнение Лагранжа второго рода.
![]()