Сверхпроводимость и низкие температуры
Содержание:
1. Вступление
2. Сверхпроводящие вещества
3. Эффект Мейснера
4. Теплоемкость сверхпроводника
5. Изотропический эффект
6. Теория сверхпроводимости
7. Конечные температуры
8. Щель в энергетическом спектре
9. Сверхпроводимость в полупроводниках
10. Эффекты Джозефсона
11. Электромагнитные свойства сверхпроводников
12. Заключение
13. Библиография
Вступление
В 1908 г. в Лейденском университете под руководством Камерлинг-Оннеса был получен жидкий гелий. Гелий отличается очень низкой температурой кипения (4,21К), и поэтому его сжижение позволило изучать свойства веществ при температурах, ранее не доступных.
1911 г. был отмечен открытием явления сверхпроводимости. Открыл его все тот же Камерлинг-Оннес в Лейденском университете, в лаборатории низких температур. Изучение этого явления составляет одно из важнейших направлений в физике твердого тела. При проведении экспериментов оказалось, что при низкой температуре сопротивление многих металлов обращается в нуль. Для первого исследованного вещества—ртути этот барьер составил 4К.
Эффект сверхпроводимости состоит в исчезновении электрического сопротивления при конечной температуре, отличной от нуля. Приблизительное сопротивление сверхпроводника: 10-23 ом*см. По проводнику, находящемуся в сверхпроводящем состоянии ток будет циркулировать бесконечно. Также у сверхпроводников наблюдается резкая аномалия магнитных, тепловых и других свойств.
Сверхпроводящие вещества
Самой высокой критической температурой среди чистых веществ обладает ниобий (9,22К), а наиболее низкой иридий (0,14К). Критическая температура зависит не только от химического состава вещества, но и от структуры самого кристалла. Например, серое олово—полупроводник, а белое может превращаться в сверхпроводящий металл. Поэтому сверхпроводимость является свойством не отдельных атомов, а представляет собой эффект структуры самого образца.
Хорошие проводники (серебро, золото и некоторые другие) не обладают этим свойством, а многие другие вещества, которые в обычных условиях проводники очень плохие—наоборот, обладают. Для исследователей это явилось полной неожиданностью и еще больше осложнило объяснение этого явления. Основную часть сверхпроводников составляют не чистые вещества, а их сплавы и соединения. Причем сплав двух несверхпроводящих веществ может обладать сверхпроводящими свойствами.
Долгие годы «рекордсменом» был сплав ниобия и олова (18,1К). Однако в 1967 г. был создан Nb3Al0,75Ge0,25 (20,1К). В 1973 создали пленку Nb3Ge (22,3К). Сейчас созданы соединения на основе керамики из оксидов металлов, критическая температура у которых выше температуры сжижения азота и приближается к комнатной.
Эффект Мейсснера
В 1933 Мейсснером и Оксенфедьдом было открыто одно из наиболее фундаментальных свойств сверхпроводимости—эффект Мейсснера. Оказалось, что магнитное поле не проникает в толщу сверхпроводящего образца. Если мы исследуем образец при t>Tk, то в образце напряженность при помещении в магнитное поле будет больше нуля. Не выключая внешнего поля, начнем постепенно понижать температуру. Тогда окажется, что магнитной поле будет постепенно вытолкнуто из сверхпроводника.
Как известно, металлы, за исключением ферромагнетиков в отсутствие внешнего магнитного поля обладают нулевой магнитной индукцией. Это связано с тем, что магнитные поля элементарных токов, которые всегда имеются в веществе, взаимно компенсируются вследствие полной хаотичности их расположения.
При коэффициенте m>1 (парамагнитные вещества) происходит уменьшение внешнего поля в образце. В диамагнитных веществах (m<1) наблюдается ослабление приложенного поля. В сверхпроводниках b=0, что соответствует нулевой магнитной проницаемости. В поверхностном слое металла возникает стационарный электрический ток, собственное магнитное поле которого противоположно приложенному полю и компенсирует его, что в результате и приводит к нулевому значению индукции в толще образца. Эффект Мейсснера и явление сверхпроводимости тесно связаны между собой и являются следствием общей закономерности, которую и установила созданная более чем через полвека после открытия явления теория сверхпроводимости.
 Существование стационарных сверхпроводящих токов обнаруживается в следующем эксперименте: если над металлическим сверхпроводящим кольцом поместить сверхпроводящую сферу, то на ее поверхности индуцируется сверхпроводящий незатухающий ток. Его возникновение приводит к диамагнитному эффекту и возникновению сил отталкивания между кольцом и сферой, в результате будет наблюдаться парение сферы над кольцом. Магнитные силовые линии не проникает в толщу образца, а находятся в поверхностном слое, где протекает незатухающий ток. Глубина проникновения поля в образец является одной из основных характеристик сверхпроводника. Обычно глубина проникновения приблизительно равна 100..400Å. Поверхностный слой сверхпроводника обладает особыми свойствами, связанными с отличной от нуля напряженностью магнитного поля в нем. Эти свойства оказывают очень существенное влияние на получение сверхпроводников с высокими критическими полями.
Существование стационарных сверхпроводящих токов обнаруживается в следующем эксперименте: если над металлическим сверхпроводящим кольцом поместить сверхпроводящую сферу, то на ее поверхности индуцируется сверхпроводящий незатухающий ток. Его возникновение приводит к диамагнитному эффекту и возникновению сил отталкивания между кольцом и сферой, в результате будет наблюдаться парение сферы над кольцом. Магнитные силовые линии не проникает в толщу образца, а находятся в поверхностном слое, где протекает незатухающий ток. Глубина проникновения поля в образец является одной из основных характеристик сверхпроводника. Обычно глубина проникновения приблизительно равна 100..400Å. Поверхностный слой сверхпроводника обладает особыми свойствами, связанными с отличной от нуля напряженностью магнитного поля в нем. Эти свойства оказывают очень существенное влияние на получение сверхпроводников с высокими критическими полями.
Если мы начнем увеличивать напряженность внешнего поля,
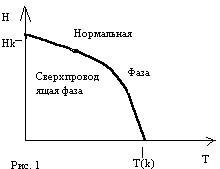
То при критическом его значении сверхпроводимость разрушится. Чем ближе мы подходим к точке критической температуры, тем меньше должна быть напряженность внешнего магнитного поля для разрушения эффекта сверхпроводимости, и наоборот, при температуре, равной температуре абсолютного нуля напряженность должна быть максимальной по отношению к другим случаям для достижения такого же эффекта. Данная взаимосвязь иллюстрируется следующим графиком (рис. 1).
Теплоемкость сверхпроводника
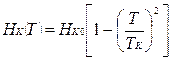 |
Чем сильнее температура приближается к критической, тем меньше величина критического поля, достаточного для разрушения сверхпроводимости. При T=Тк Hk=0; приблизительно зависимость критического поля от температуры выражается следующей формулой:
Теплоемкость металла складывается из электронной теплоемкости и теплоемкости кристаллической решетки. При низких температурах основной вклад в теплоемкость металла вносит электронная система. Электронная теплоемкость нормального металла соответствует отношению:
Теплоемкость же решетки при понижении температуры падает не пропорционально, а по следующей формуле, поэтому ею можно пренебречь:
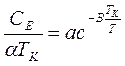 |
В сверхпроводниках Се убывает и при температуре, стремящейся к нулю, тоже стремится к нулю по экспоненциальному закону.
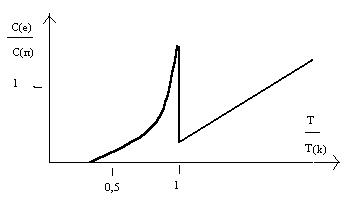 Где A и b постоянные, не зависящие от температуры величины. Когда температура сверхпроводника становится равной критической, происходит переход в нормальное состояние и теплоемкость начинает изменяться по линейному закону. Весьма своеобразны свойства теплопроводности в сверхпроводнике. При наличии дифференциального градиента температуры металл не находится в состоянии теплового равновесия. В образце возникает тепловой поток, пропорциональный созданному температурному градиенту. Связь между ними определяется по формуле:
Где A и b постоянные, не зависящие от температуры величины. Когда температура сверхпроводника становится равной критической, происходит переход в нормальное состояние и теплоемкость начинает изменяться по линейному закону. Весьма своеобразны свойства теплопроводности в сверхпроводнике. При наличии дифференциального градиента температуры металл не находится в состоянии теплового равновесия. В образце возникает тепловой поток, пропорциональный созданному температурному градиенту. Связь между ними определяется по формуле:
![]()
Общий коэффициент теплопроводности складывается из коэффициента теплопроводности электронной системы и коэффициента теплопроводности решетки:
![]()
Коэффициент же теплопроводности электронной системы в свою очередь складывается из коэффициента электронной решетки и коэффициента рассеяния примесями.
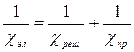 |
В образцах, содержащих малые концентрации примеси основную роль играет электронная теплопроводность, зависящая от температуры по закону:
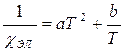 |
В образцах, содержащих малые концентрации примесей, основную роль играет электронная теплопроводность, зависящая от Т по следующему правилу:
 Слагаемые в правой части формулы соответствуют χреш, χэл. При переходе металла в сверхпроводящее состояние скачком обращается в нуль сопротивление. Поэтому электронная теплопроводность тоже должна равняться нулю. Тогда при прохождении через критическую температуру должен был бы наблюдаться скачок теплопроводности. Однако этого не происходит. Электронная теплопроводность падает, но остается отличной от нуля.
Слагаемые в правой части формулы соответствуют χреш, χэл. При переходе металла в сверхпроводящее состояние скачком обращается в нуль сопротивление. Поэтому электронная теплопроводность тоже должна равняться нулю. Тогда при прохождении через критическую температуру должен был бы наблюдаться скачок теплопроводности. Однако этого не происходит. Электронная теплопроводность падает, но остается отличной от нуля.
Для объяснения этого явления была предложена двужидкостная модель. В двужидкостной модели предполагается, что электронную «жидкость» в сверхпроводнике можно представить как совокупность двух жидкостей—нормальной и сверхпроводящей. Нормальная компонента ничем не отличается по своим свойствам от электронной системы нормального образца, сверхпроводящий же—аномален. При повышении температуры количество нормального компонента возрастает, а количество аномального уменьшается и наоборот. В нормальном металле число электронов, участвующих в теплопередаче не меняется в зависимости от температуры, а в сверхпроводящем зависит. Аномальный компонент отвечает за проведение токов, а нормальный—за обычную теплопроводность (χэл) и за рассеивание. Уменьшение числа переносящих энергию носителей естественно приводит к уменьшению χэл.
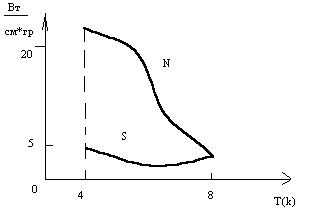
Решеточную проводимость можно себе представить, как перенос энергии звуковыми квантами—фононами, фононы—это колебания решетки кристалла. Сверхпроводящий переход не меняет состояния кристаллической решетки, однако уменьшение нормальной составляющей, с которой взаимодействуют фононы, осложняет картину—убывание числа фононов сопровождается гораздо более эффективным увеличением длины их свободного пробега, что приводит к росту решеточной теплопроводности. Рост продолжается до тех пор, пока длина пробега не станет больше длины, Обусловленной взаимодействием с примесями и границами кристалла. Тогда последний вид рассеяния начинает играть основную роль, и χреш начинает уменьшаться из-за уменьшения при температурах, близких к абсолютному нулю числа фононов. Сверхпроводимость представляет собой коллективный квантовый эффект кристаллической структуры вещества.
Изотропический эффект
Историческое значение изотропического эффекта во многом состоит именно в том, что он указывал исследователям направление дальнейших поисков по созданию всеобъемлющей теории, объясняющей причину возникновения множества аномалий, которые возникали в веществах, находящихся в сверхпроводящем состоянии.
Исследование различных сверхпроводящих изотопов ртути привело к установлению связи между критической температурой и массой изотопов. Оказалось, что при изменении массового числа М от 199,5 до 203,4 наблюдается изменение критической температуры веществ от 4,185К до 4,140К. С достаточной точностью удалось установить справедливость следующей формулы:
Масса изотопа является характеристикой структуры кристаллической решетки вещества и может влиять на ее свойства. Так, например, частота решеточных колебаний связана с массой ионов соотношением:
Сверхпроводимость, которая является свойством электронной системы металла, оказывается связанной, ввиду обнаружения изотропического эффекта, с состоянием кристаллической решетки. Следовательно, возникновение эффекта сверхпроводимости обусловлено взаимодействием электронов с решеткой металла. Это взаимодействие ответственно за сопротивление металла в обычном состоянии. При определенных условиях оно должно приводить к исчезновению сопротивления, то есть к эффекту сверхпроводимости.
Теория сверхпроводимости
В 1957 г. Бардином, Купером и Шриффером была построена последовательная теория сверхпроводящего состояния вещества (теория БКШ). Отличный от развитого в теории БКШ, новый метод в теории сверхпроводимости был разработан Н. Н. Боголюбовым.
Открытие изотропического эффекта явно указывало на то, что при объяснении явления сверхпроводимости необходимо учитывать взаимодействие электронов с кристаллической решеткой кристалла. Электрон, движущийся в металле, электрическими силами деформирует—поляризует—кристаллическую решетку образца. Вызванное этим смещение ионов решетки отражается на состоянии другого электрона, поскольку он теперь оказывается в поле поляризованной решетки, несколько изменившей свою периодическую структуру. Таким образом, кристаллическая решетка выступает в роли промежуточной среды в межэлектронных взаимодействиях, так как с ее помощью электроны реализуют притяжение друг к другу. При высоких температурах достаточно интенсивное тепловое движение отбрасывает частицы друг от друга, фактически уменьшая силу притяжения. Но при низких температурах силы притяжения играют очень важную роль.
Два электрона отталкиваются друг от друга, если находятся в пустоте. В среде же сила их взаимодействия равна:
(где ε—диэлектрическая проницаемость среды). Если среда такова, что ε<0, то одноименные заряды, в том числе и электроны, будут притягиваться. Кристаллическая решетка некоторых веществ является той средой, в которой выполняется это условие, а значит при определенных температурах возможно возникновение эффекта сверхпроводимости. Таким образом эффект взаимного притяжения электронов не противоречит законам физики, так как происходим в некоторой среде.
Рассмотрим металл при Т=0К. Его кристаллическая решетка совершает «нулевые» колебания, существование которых связано с квантовомеханическим соотношением неопределенностей. Электрон, движущийся в кристалле, нарушает режим колебаний и переводит решетку в возбужденное состояние. Обратный переход на прежний энергетический уровень сопровождается излучением энергии, захватываемой другим электроном и возбуждающей его. Возбуждение кристаллической решетки описывается звуковыми квантами—фононами, поэтому описанный выше процесс можно представить как излучение фонона одним электроном и поглощение его другим электроном, кристаллическая решетка же играет промежуточную роль передатчика. Обмен фононами обуславливает их взаимное притяжение.
При низких температурах это притяжение у ряда веществ преобладает над кулоновскими силами отталкивания электронов. При этом электронная система превращается в связанный коллектив, и чтобы ее возбудить требуется затрата некоторой конечной энергии. Энергетический спектр электронной системы в этом случае не будет непрерывным—возбужденное состояние отделено от основного энергетической щелью.
При наличии щели в энергетическом спектре квантовые переходы системы не всегда будут возможны. Электронная система не будет возбуждаться при малых скоростях движения, следовательно, движение электронов будет происходить без трения, что означает отсутствие сопротивления. При определенном критическом токе электронная система сможет перейти на следующий энергетический уровень и сверхпроводимость разрушится.
Хорошие проводники не обладают эффектом сверхпроводимости, так как хорошая проводимость говорит о низком сопротивлении материала и о слабом взаимодействии электронов с кристаллической решеткой. Оно не создает при температуре около абсолютного нуля достаточной силы межэлектронного притяжения, способной преодолеть кулоновскую силу отталкивания.
Электронную систему в сверхпроводнике можно представить как состоящую из связанных пар электронов (куперовских пар), а возбуждение, как разрыв пары. Размер электронной пары составляет приблизительно ξ0~10е-4 см, размер периода решетки—10е-8 см. То есть электроны в паре находятся на огромном расстоянии.
![]() Электроны в металле при абсолютном нуле принимают значение энергии ξf (уровень Ферми). Равенство ξ(ρ)=ξf определяет в ρ-пространстве поверхность Ферми. В случае
Электроны в металле при абсолютном нуле принимают значение энергии ξf (уровень Ферми). Равенство ξ(ρ)=ξf определяет в ρ-пространстве поверхность Ферми. В случае
Поверхность является сферой.
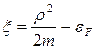 |
Сверхпроводимость обусловлена взаимодействием электронов с кристаллической решеткой. Энергия фонона ħω не может быть сколь угодно большой, максимальная энергия фонона соответствует в температурной шкале дебаевской температуре θ. Поэтому переходить в связанное состояние могут только электроны около уровня Ферми в слое толщиной ħώ (средняя частота колебаний фонона). Наличие притяжения приводит к перестройке поверхности Ферми, связанной с появлением энергетической щели. Если в нормальном металле электрическая энергия, отсчитанная от значения εf равна
то есть может быть сколь угодно малой величиной, то в сверхпроводнике
Отсюда следует, что наименьший уровень энергии, соответствующий ξ=0 отличен от нуля и равен энергетической щели.
Конечные температуры
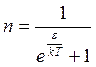 Хаотическое тепловое движение приводит к возбуждению электронной системы и ослабляет притяжение между электронами. В сверхпроводнике при температуре выше абсолютного нуля появляются квазичастицы, которыемогут менять свою энергию на сколь угодно малую величину и поэтому ведут себя как обычные электроны. Они описываются распределением Ферми-Дирака:
Хаотическое тепловое движение приводит к возбуждению электронной системы и ослабляет притяжение между электронами. В сверхпроводнике при температуре выше абсолютного нуля появляются квазичастицы, которыемогут менять свою энергию на сколь угодно малую величину и поэтому ведут себя как обычные электроны. Они описываются распределением Ферми-Дирака:
где
Δ(Т)—энергетическая щель при данной температуре. Число квазичастиц данной энергии меньше соответствующего числа электронов в нормальном металле. При Т→0 число квазичастиц тоже стремится к нулю. При температуре, близкой к нулевой, n (число частиц) экспоненциально малая величина, а при Т≥Тк, когда Δ=0, функция переходит в выражение, описывающее обычные электроны в нормальном металле. При температуре меньшей критической число квазичастиц меньше, чем общее число электронов. Таким образом, реализуется «двужидкостная» модель. Тепловое движение при конечных температурах приводит к ослаблению сверхпроводящего упорядочивания, вследствие появления квазичастиц. Электроны в сверхпроводнике не разделены строго на две категории, поэтому наблюдается постоянный взаимопереход квазичастиц и куперовских пар.
Электронная теплопроводность в сверхпроводниках, содержащих небольшие количества примесей выражается формулой:
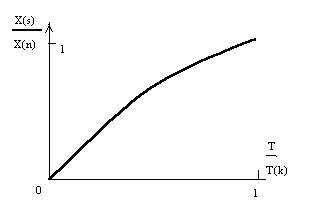
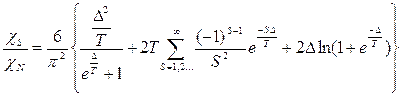 |
Данное отношение является универсальной функцией температуры. В сверхпроводниках с примесями основную роль играет тепловой поток в решетке кристалла, возрастающий с понижением температуры.
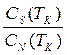 |
Теория сверхпроводимости позволяет описать температурную зависимость теплоемкости сверхпроводника. Поскольку число квазичастиц экспоненциально падает с понижением температуры, то и электронная теплоемкость тоже стремится к нулю при Т→0 по экспоненте. При Т=Тк теория предсказывает скачок теплоемкости:
Щель Δ(Т) с ростом температуры уменьшается. Для Тк:
где р--константа связи электронов. Отсюда следует: Тк~ώ, то есть ,то
таким образом, объясняется изотропический эффект.
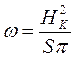 Разность энергий нормальной и сверхпроводящей фаз на единицу объема составляет
Разность энергий нормальной и сверхпроводящей фаз на единицу объема составляет
(Нк—критическое поле)
При Н=Нк металл переходит в нормальное состояние.
Щель в энергетическом спектре
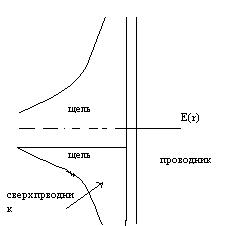
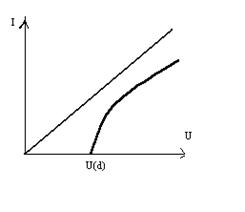 Энергетическая щель в сверхпроводниках непосредственно наблюдается на опыте. При этом не только подтверждается существование щели в спектре, но и измеряется ее величина. Исследовался переход электронов через тонкий непроводящий слой толщиной ~10Å, разделяющий нормальную и сверхпроводящую пленки. При наличии барьера имеется конечная вероятность прохождения электрона через барьер. В нормальном металле заполнены все уровни энергии, вплоть до максимального εf, в сверхпроводящем же до εf-Δ. Прохождение тока при этом невозможно. Наличие энергетической щели в сверхпроводнике приводит к отсутствию соответствующих состояний, между которыми происходил бы переход. Для того чтобы переход мог произойти, необходимо поместить систему во внешнее электрическое поле. В поле вся картина уровней смещается. Эффект становится возможным, если приложенное внешнее напряжение становится равным Δ/e. На графике видно, что туннельный ток появляется при конечном напряжении U, когда eU равно энергетической щели. Отсутствие туннельного тока при сколь угодно малом приложенном напряжении является доказательством существования энергетической щели.
Энергетическая щель в сверхпроводниках непосредственно наблюдается на опыте. При этом не только подтверждается существование щели в спектре, но и измеряется ее величина. Исследовался переход электронов через тонкий непроводящий слой толщиной ~10Å, разделяющий нормальную и сверхпроводящую пленки. При наличии барьера имеется конечная вероятность прохождения электрона через барьер. В нормальном металле заполнены все уровни энергии, вплоть до максимального εf, в сверхпроводящем же до εf-Δ. Прохождение тока при этом невозможно. Наличие энергетической щели в сверхпроводнике приводит к отсутствию соответствующих состояний, между которыми происходил бы переход. Для того чтобы переход мог произойти, необходимо поместить систему во внешнее электрическое поле. В поле вся картина уровней смещается. Эффект становится возможным, если приложенное внешнее напряжение становится равным Δ/e. На графике видно, что туннельный ток появляется при конечном напряжении U, когда eU равно энергетической щели. Отсутствие туннельного тока при сколь угодно малом приложенном напряжении является доказательством существования энергетической щели.
Величины: Δ(0)/kT
| Величина | Al | In | Sn | Pb | Теория |
| 2Δ(0)/kTk | 3,37 | 3,45 | 3,47 | 4,26 | 3,52 |
Другой метод, позволяющий сделать выводы, связан с эффектом прохождения инфракрасного электромагнитного излучения через тонкие сверхпроводящие пленки. При частотах, удовлетворяющих условию ħω=2Δ наблюдается пик в поглощении длинноволнового электромагнитного излучения, что позволяет определить величину щели. При меньших частотах наблюдается сверхпрозрачность образцов. Опыты такого рода были проведены, однако они являются менее надежными по сравнению с туннельными экспериментами. Некоторые результаты этих опытов представлены в таблице.
Определить величину энергетической щели можно также, изучая поглощение ультразвука в сверхпроводниках. Оно определяется по следующей формуле:
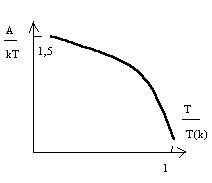 Где v—коэффициент поглощения ультразвука. Данная формула справедлива при условии w<<2Δ/ħ.
Где v—коэффициент поглощения ультразвука. Данная формула справедлива при условии w<<2Δ/ħ.
В сверхпроводниках звук поглощается слабее, чем в нормальных металлах, при Т=0 VS=0. Физически это связано с наличием энергетической щели. Звуковой квант, энергия которого мала, не может перевести в возбужденное состояние электронную систему. При конечной температуре ультразвук поглощается «нормальным» компонентом электронной системы.
Сверхпроводимость в полупроводниках
В полупроводниках концентрация электронов меньше, чем в металлах, и это обстоятельство препятствует куперовских пар электронов, характерных для сверхпроводящего состояния.
Кулоновское отталкивание, препятствующее межэлектронному притяжению, оказывается тоже значительно ослабленным. Данные факты не исключают возможности наблюдения сверхпроводимости у полупроводников. В 1963 г. был установлен факт наличия сверхпроводящих свойств у полупроводников: GeTe (TK=0,08K); SrTiO3 (TK=0,3K). Характерно, что у SrTiO3 диэлектрическая проницаемость очень велика (~10е4), то есть кулоновское отталкивание было в значительной мере ослаблено. Концентрация донорно-акцепторных примесей в этих полупроводниках довольно велика, по своим свойствам они являются выраженными полупроводниками и по проводимости приближаются к плохо проводящим металлам. Была обнаружена сверхпроводимость и у германия с кремнием. При обычных условиях эти элементы являются полупроводниками. Переход в сверхпроводящее состояние у них оказывается возможным лишь при высоком давлении (~100кБар). При этом происходят структурные превращения, и полупроводники переходят в металлическое состояние.
На опыте отмечают зависимость критической температуры некоторых веществ от концентрации носителей заряда n. При повышении концентрации критическая температура вначале возрастает, и после некоторого пикового значения начинает убывать.
Эффекты Джозефсона
Живший в середине 20 века английский физик-теоретик Джозефсон предсказал два эффекта связанных с протеканием токов через туннельные контакты.
Различают стационарный и нестационарный эффекты Джозефсона. Первый из них состоит в возможности протекания постоянного тока через туннельный контакт, образованный двумя сверхпроводниками, разделенными тонким слоем (~10е-7 см) диэлектрика. Ток протекает через барьер, характеризующийся нулевой разностью потенциалов.
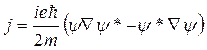 |
Исходя из квантовомеханического выражения для плотности тока:
и учитывая, что ψ—это комплексная величина:
легко находим, что j~Ñy. В реальных металлах, в отсутствие внешнего поля, макроскопический ток не наблюдается, так как фазы у электронов случайны и плотность тока обращается в нуль.
Сверхпроводники характеризуются фазовой когерентностью. При этом все электронные пары в данном сверхпроводнике имеют одинаковую фазу и ток отсутствует (Dj=0). Если образовать туннельный контакт из двух различных сверхпроводников, то через такой контакт ток потечет без приложения напряжения, он будет зависеть от разности фаз j=j1-j2 (плотность тока (тока Джозефсона) равна j=j0sinj). Это явление непосредственно определяется такой фундаментальной квантовомеханической характеристикой, как фаза волновой функции.
Если к контакту приложить постоянную разность потенциалов, то через него потечет переменный сверхпроводящий ток. Возникающие в сверхпроводнике куперовские пары проходят через диэлектрический слой и приобретают при этом энергию 2eU. Так как сопротивление отсутствует, то полученная энергия излучается в виде кванта с энергией ħn=2eU. На опыте и наблюдается электромагнитное излучение с частотой n=2eU/ħ (излучать электромагнитное волны может только переменный ток—именно он течет через контакт Джозефсона). В выражение для частоты излучения входит удвоенный заряд электрона, так как волны излучаются электронными парами. То, что частота излучения соответствует вышеприведенной формуле, является экспериментальным доказательством наличия в проводнике куперовских пар электронов. Эффект Джозефсона позволяет создавать переменный ток с помощью постоянной разности потенциалов.
Эффект Джозефсона используется в работе мощных сверхпроводящих квантовых генератов.
Электромагнитные свойства сверхпроводников
Электронную систему в сверхпроводнике можно представить, состоящей из связанных пар электронов, причем размер пары весьма велик (~10e-4 cм). Постоянный электрический ток в нормальном металле подчиняется закону Ома, сила тока в какой-либо точке определяется значением напряженности поля в той же точке (локальная связь).
В сверхпроводящем образце сопротивление постоянному току равно нулю, а электрическое поле отсутствует. Поверхностный сверхпроводящий ток возникает при помещении во внешнее поле. Сверхпроводящий ток в данной точке не определяется состоянием поля в данной конкретной точке, а зависит от состояния поля в некоторой окрестности этой точки.
Заключение
Эффект сверхпроводимости применяется во многих отраслях человеческой деятельности. Исследование способов увеличения критического магнитного поля позволяет создавать сверхпроводники, имеющие возможность пропускать высокие токи. На электростанциях достаточно давно применяются криотурбогенераторы, способные увеличивать мощность станций примерно на 40%. С явлением сверхпроводимости неразрывно связан наблюдаемый в жидком гелии эффект сверхтекучести. Жидкий гелий является уникальной жидкостью, часто его называют квантовой жидкостью, так как многие его макросвойства являются прямым отражением событий, происходящих на уровне атомов и элементарных частиц. Открытие сверхпроводимости было бы невозможно без создания технологии сжижения гелия. Особое применение имеет эффект Мейсснера—свойство отталкивания использоваться в создании магнитной подушки, применяемой в создании многих новых видов транспорта. Сверхпроводимость имеет также огромное значение для более глубокого понимания процессов, происходящих на уровне внутреннего строения атомов.
Библиография
1. Кресин В.Л. «Сверхтекучесть и сверхпроводимость», издательство «Мир», 1989 г., 214 стр.
2. Тилле Дж. «Сверхпроводимость и сверхтекучесть», издательство «Москва», 1986 г., 302 стр.
3. Ландау Л.Д. «Физика», издательство «Физмат», 1993 г., 540 стр.
4. Регалин С.М. «Введение в теорию сверхпроводимости», 1981 г., 156 стр.
5. Эдельман К.М. «Физика низких температур», 1992 г., 230 стр.