Поля и Волны
Лекция 7
Плоские электромагнитные
волны
7.1. Понятие волнового процесса.
7.2. Плоские волны в идеальной среде.
7.3. Плоские волны в реальных средах.
7.4.Распространение волнового пакета. Групповая скорость.
7.5. Поляризация ЭМВ.
7.1. Понятие волнового процесса.
Мир, в котором мы живем, - мир волн. Чем характеризуется мир волн, волновых процессов ?
Волновой процесс имеет следующие характерные признаки:
Волновой процесс всегда переносит энергию и импульсы. Нас интересуют волновые процессы ЭМВ.
Конечная скорость всех волновых процессов. В случае ЭМВ - это скорость света.
Независимость волновых процессов друг от друга. В этой комнате существуют поля самых разных частот, поля р/станций, света и т.д.
Волновые процессы, различные по физической природе, описываются одним и тем же математическим аппаратом.
Под волновым процессом понимают возмущение некоторой величины в пространстве, перемещающееся с конечной скоростью, переносящее мощность без переноса вещества.
7.2. Плоская ЭМВ в идеальной среде.
Под плоской ЭМ волной понимают волновой процесс, у которого составляющие электрического и магнитного полей изменяются в одинаковой фазе в плоскости перпендикулярной направлению распространения.
(7.2.1.) rot H = j a E Используем для анализа
1 - е и 2 - е уравнения
(7.2.2.) rot E = - j a H Максвелла
Источники, создающие плоские волны не входят в эти уравнения. Мы рассматриваем волновые процессы в дальней зоне, т.е. в пространстве за пределами
зарядов и токов. Решим уравнения относительно Е и Н.
Из уравнения (7.2.1.) выразим Е и подставим в (7.2.2.):
E = (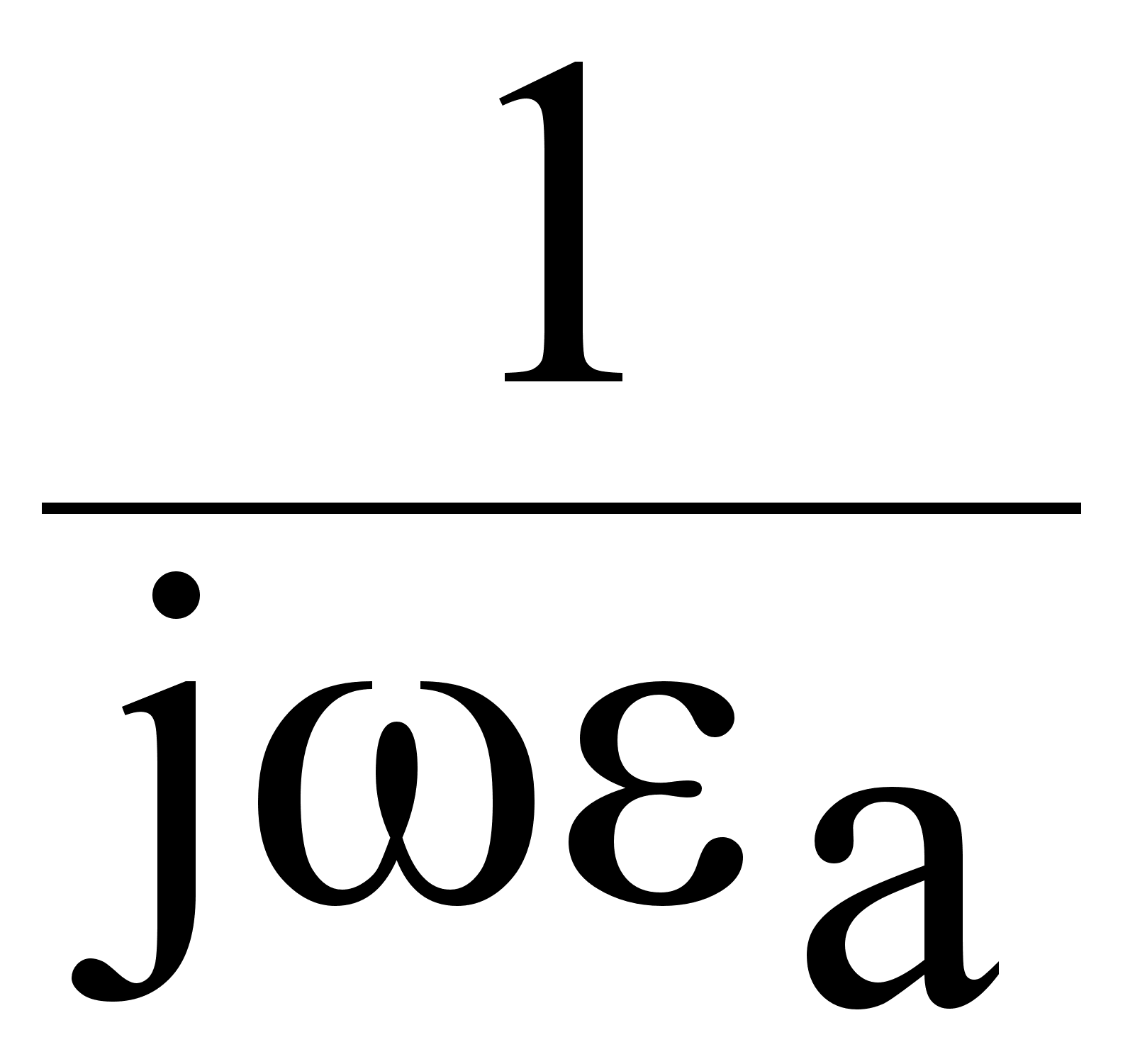 ) rot H
) rot H
(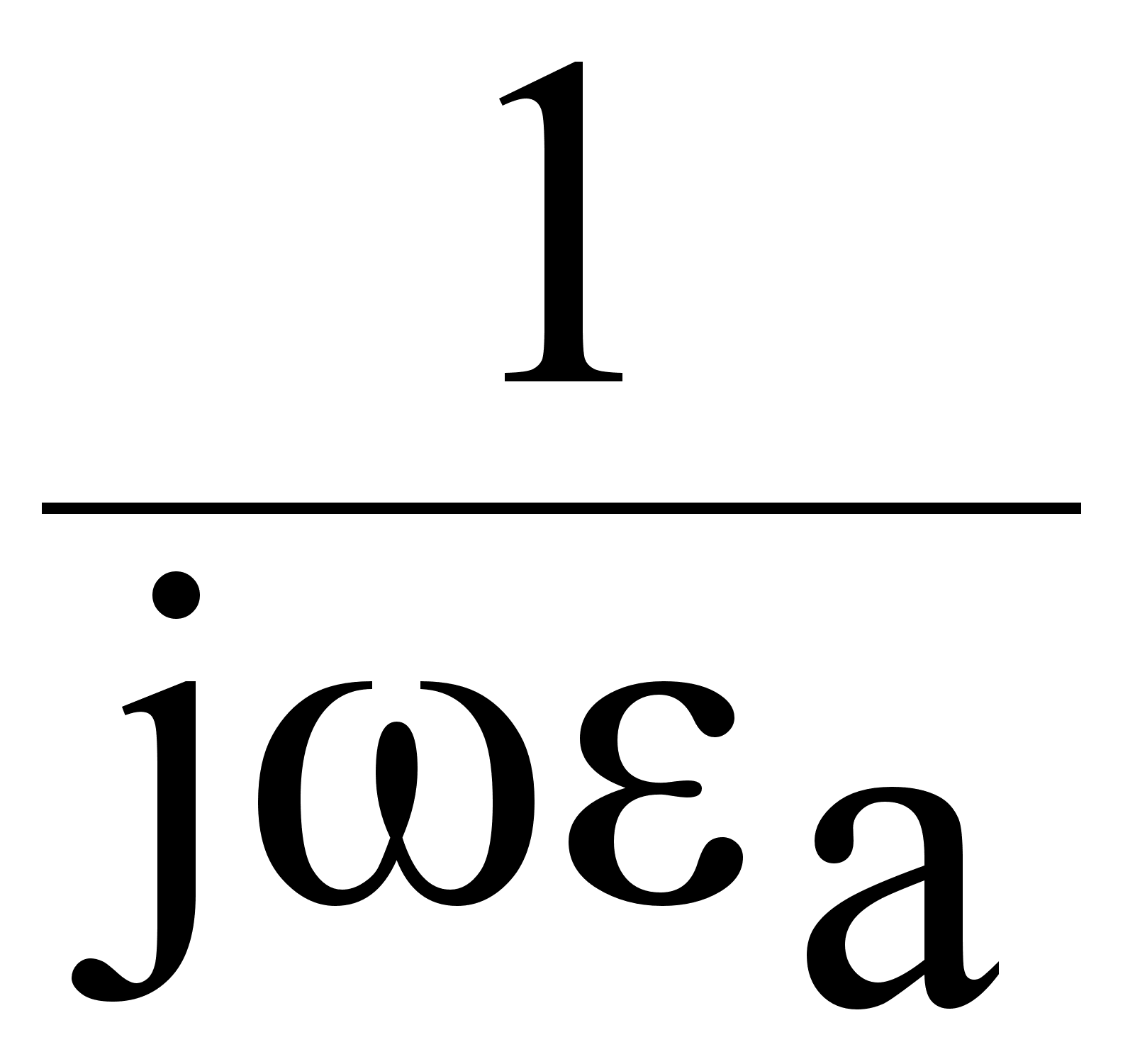 ) rot (rot H) = - ja H
) rot (rot H) = - ja H
rot rot H = grad div A - 2 H
grad div H - 2 H = 2aa H
т.к. div H = 0 - четвертое уравнение Максвелла
2 H + k2 H = 0 однородное волновое ур-е Гельмгольца (7.2.3.)
k2 = 2aa
Точно так же из второго уравнения получаем
уравнения для вектора Е:
2 E + k2 E = 0 - однородное волновое ур-е Гельмгольца (7.2.4.)
В развернутом виде запишем уравнения:
(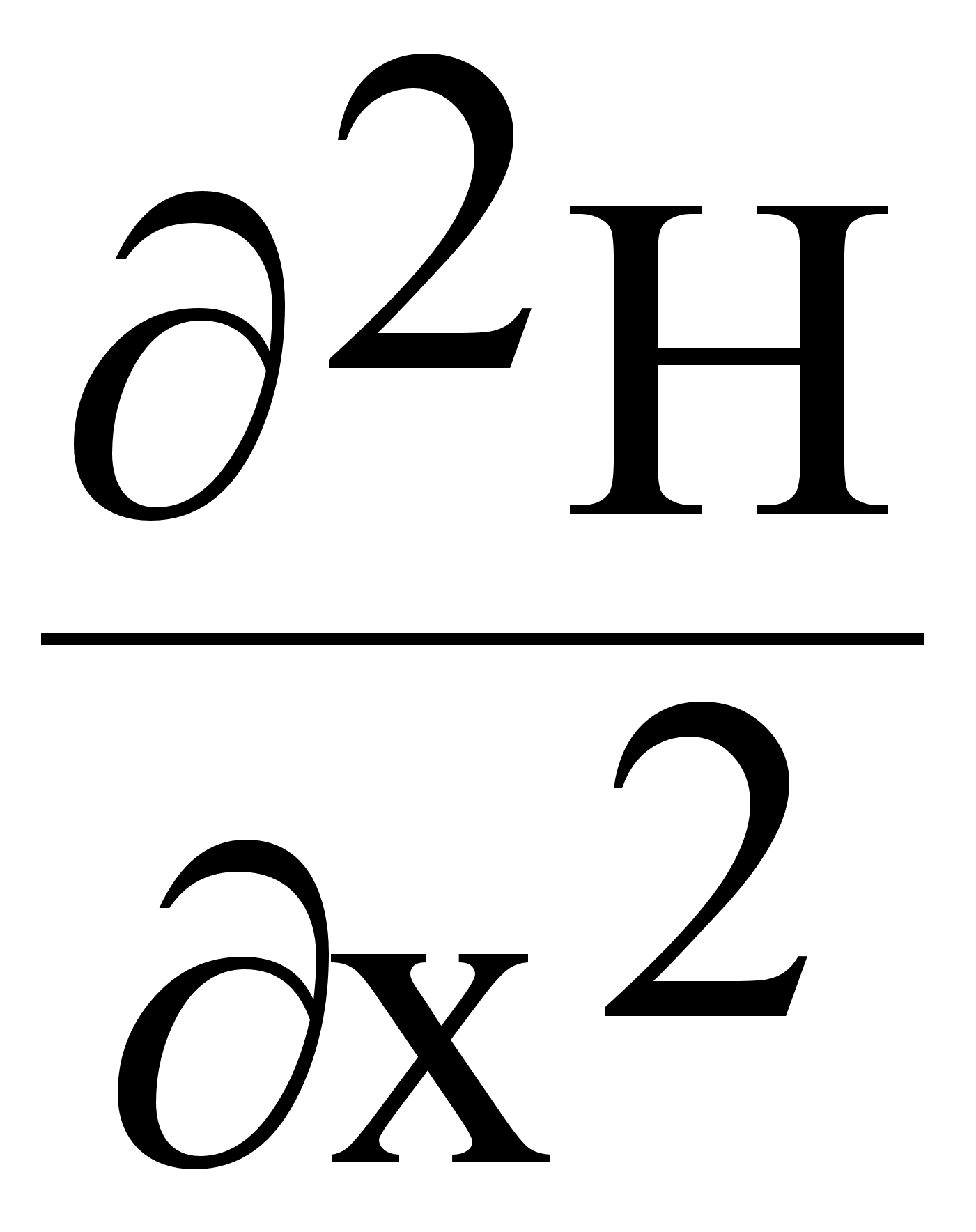 ) +(
) +(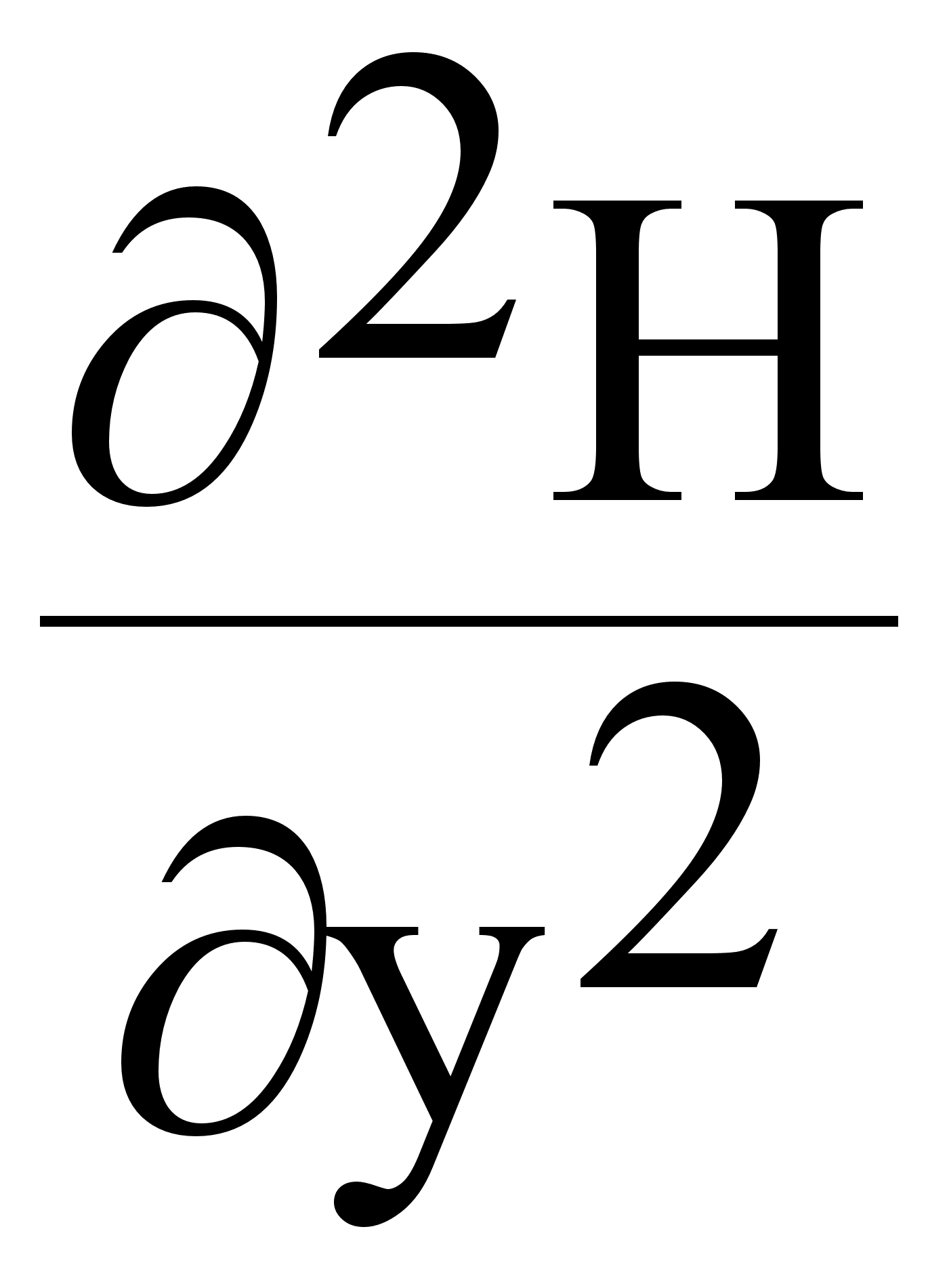 ) +(
) +(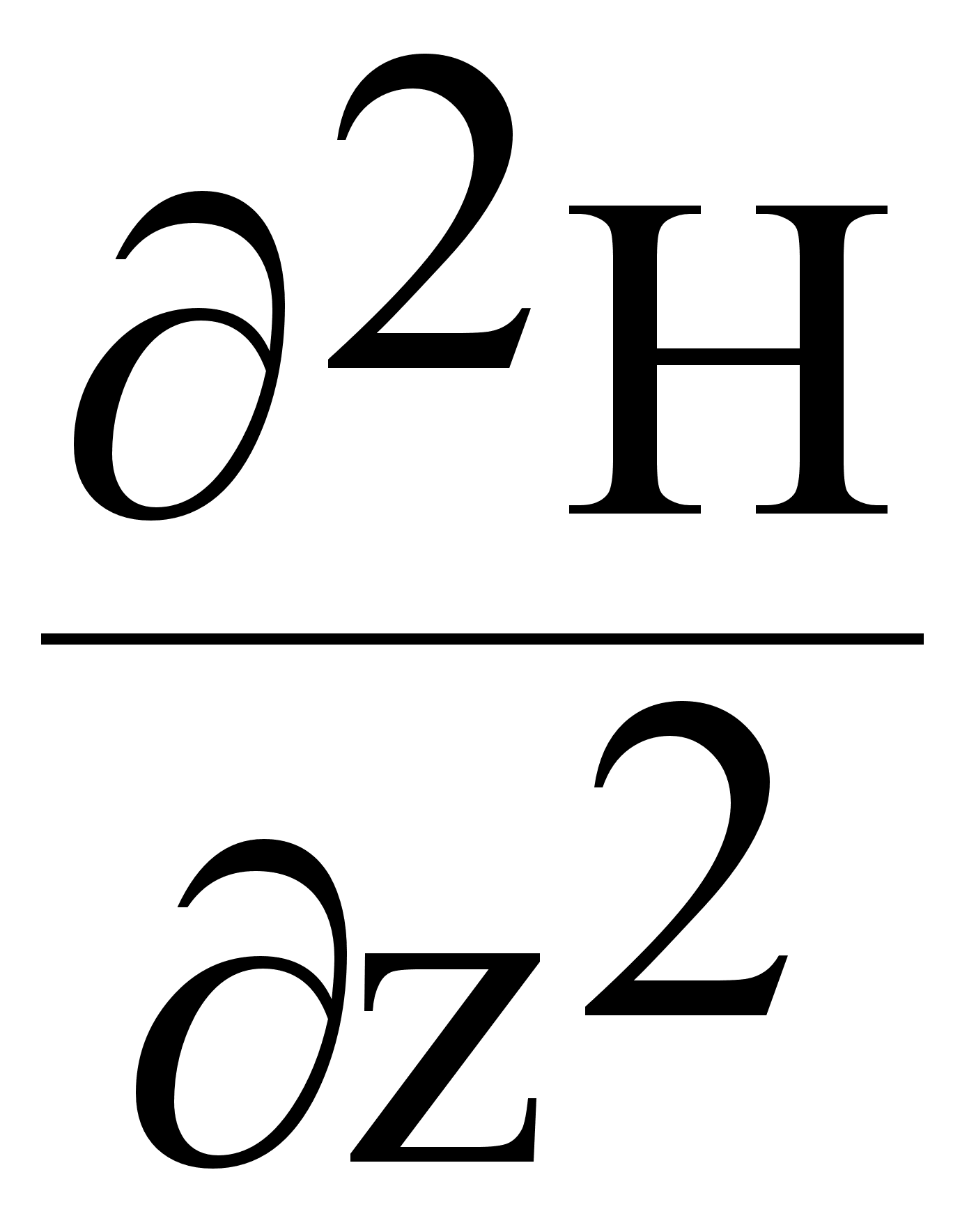 ) + k2 H = 0 (7.2.5.)
) + k2 H = 0 (7.2.5.)
Решать такое уравнение трудно. Предположим, что источник ЭМ колебаний находится очень далеко от той области, где рассматриваем волны.
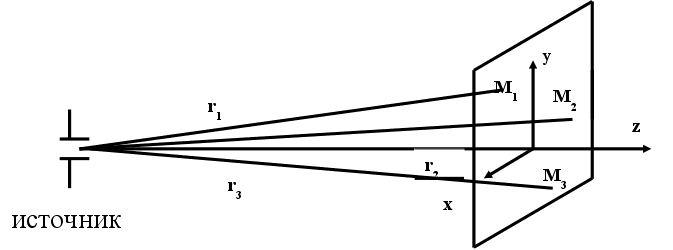
r1 r2 r3
т.к. источник очень далеко, то расстояния до точки можно считать одинаковым. Из физического смысла задачи, можно утверждать, что изменения полей по координате y, х нет, т.е.:
![]() =
=![]() = 0
= 0
(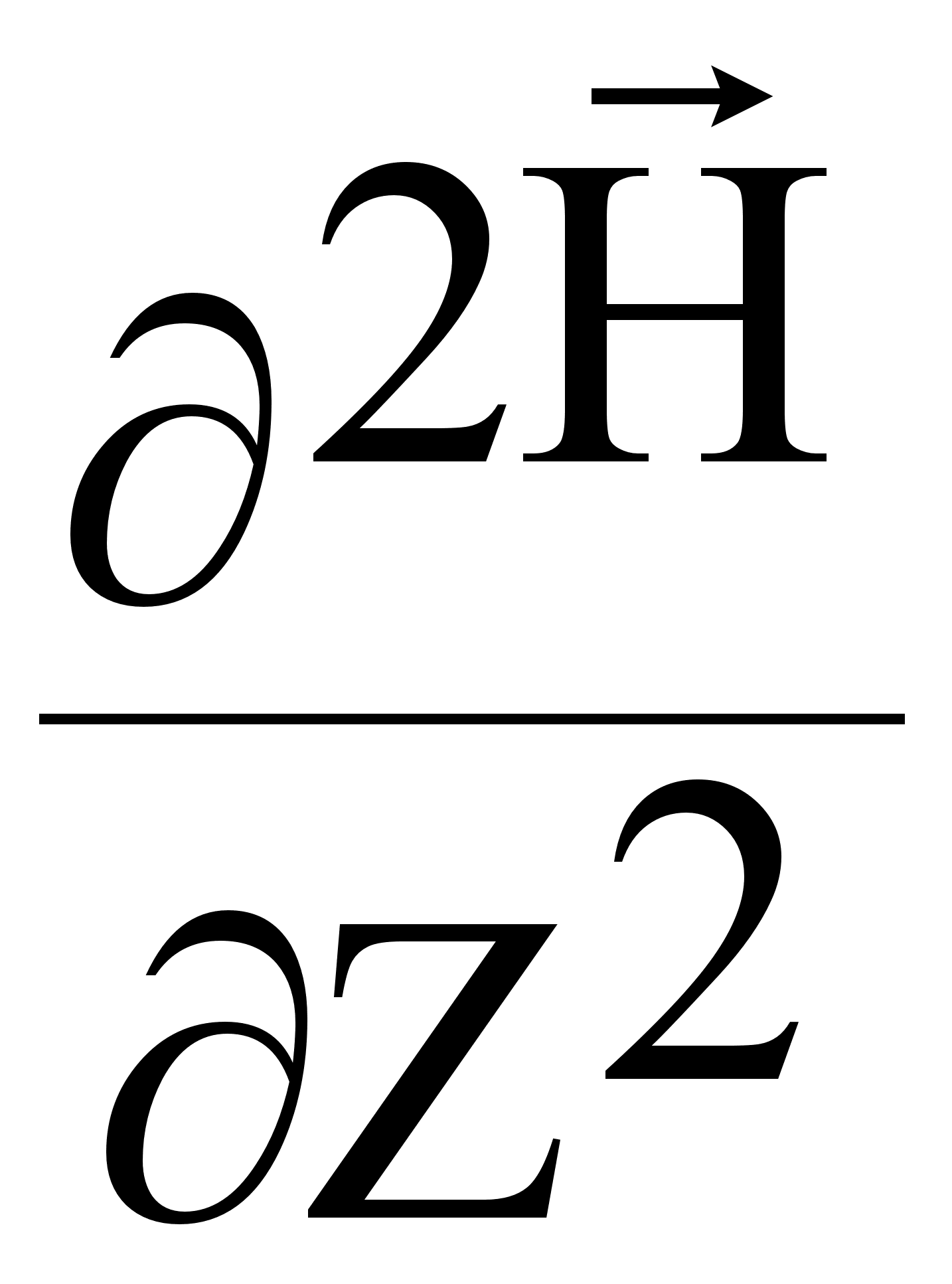 ) + k2 H = 0 (7.2.6.)
) + k2 H = 0 (7.2.6.)
Для плоской ЭМВ волновое уравнение упрощается. Решение уравнения:
H(z) = A e - jkz + B e jkz в обычной форме
H(z,t) = ejt (A e - jkz + B e jkz) если поле зависит от времени.
H(z,t) = h означает, что поле векторное.
H(z,t) = h (A ej(t-kz) + B e j(t+kz)) (7.2.7.)
Выделим составляющую поля c амплитудой А:
Ha(z,t) = h A e j(t-kz) - в комплексной форме.
(7.2.8.)
Выделим из комплексного выражения действительную часть:
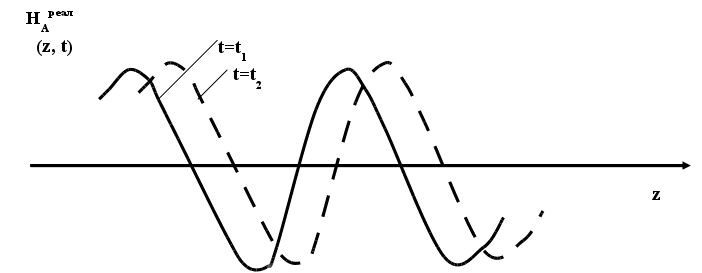
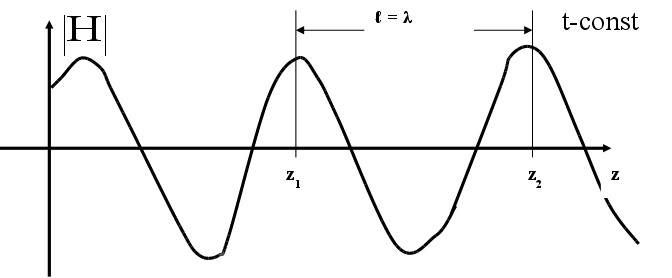
Haреал(z,t) = Re Ha(z,t) = h A cos(t - kz) (7.2.9.)
![]()
![]()
![]()
![]()
z1 z2
Фотография процесса в момент времени t = t1, t = t2. С какой скоростью перемещается фронт с одинаковой фазой ? Выясним это:
Ф1 = t1 - kz1 ; Ф2 = t2 - kz2 (7.2.10.)
Прибор регистрирует одинаковую напряженность, надо потребовать, чтобы Ф1 = Ф2
t1 - kz1 = t2 - kz2
k (z2 - z1) = (t2 - t1)
 = Vф - называется фазовой скоростью волны.
= Vф - называется фазовой скоростью волны.
![]() k = aa
k = aa
Vф = 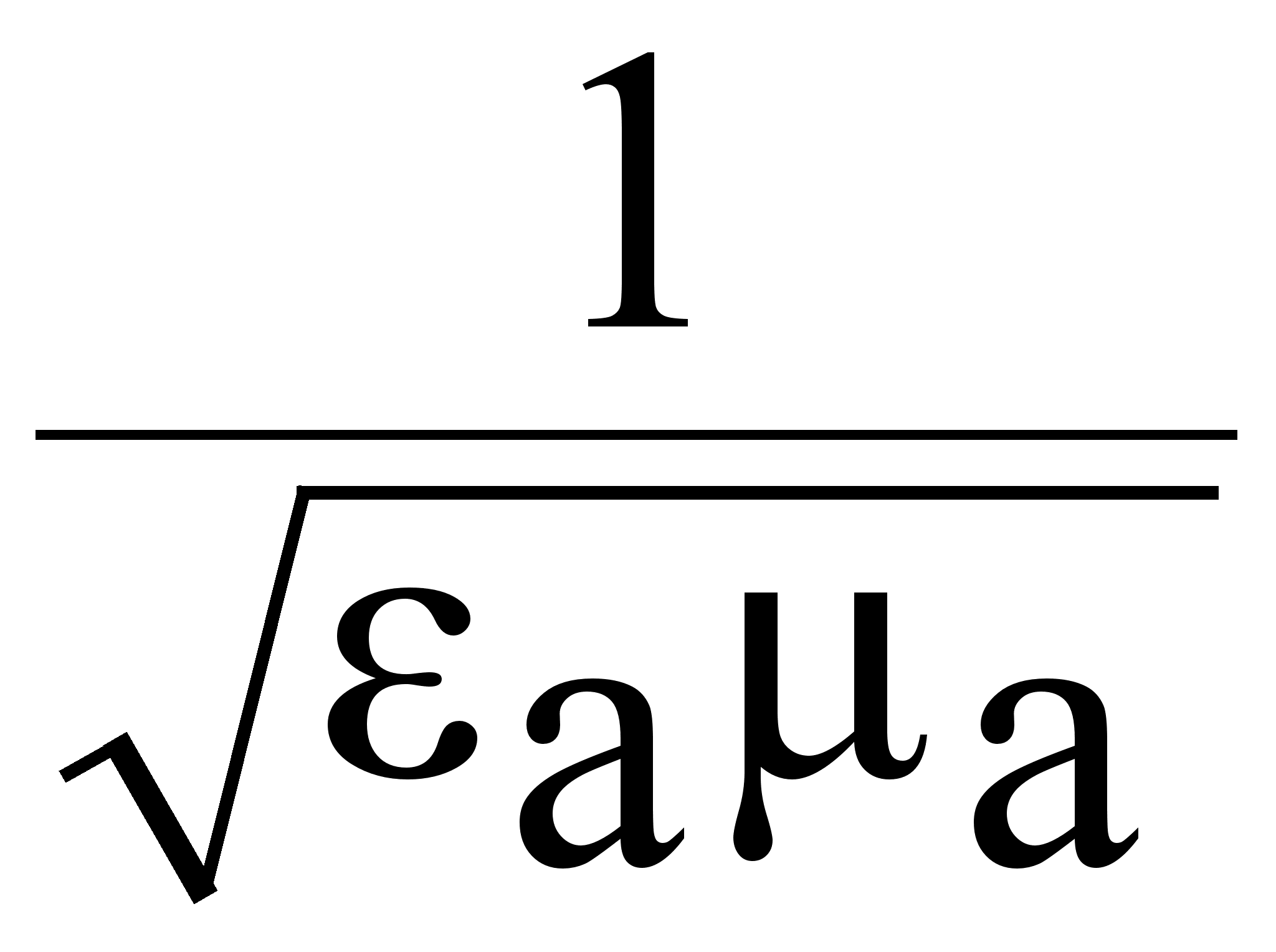 - зависит от свойств среды,
- зависит от свойств среды,
где распространяется ЭМВ.
0 = 8,85*10 –12![]() , 0 = 4*10-7
, 0 = 4*10-7![]() ,
,
V = 3*108![]() (7.2.11.)
(7.2.11.)
- называют пространственную периодичность волнового процесса.
- это длина пути, которую проходит фронт с одинаковой фазой за период, или- это есть расстояние, которое проходит фазовый фронт за 1 период.
в т. Z1 Ф1 = t - kz1
в т. Z2 Ф2 = t - kz2
Ф1 - Ф2 = 2
z2 - z1 = ![]() =
=
k = ![]() - волновое число
- волновое число
Vф = 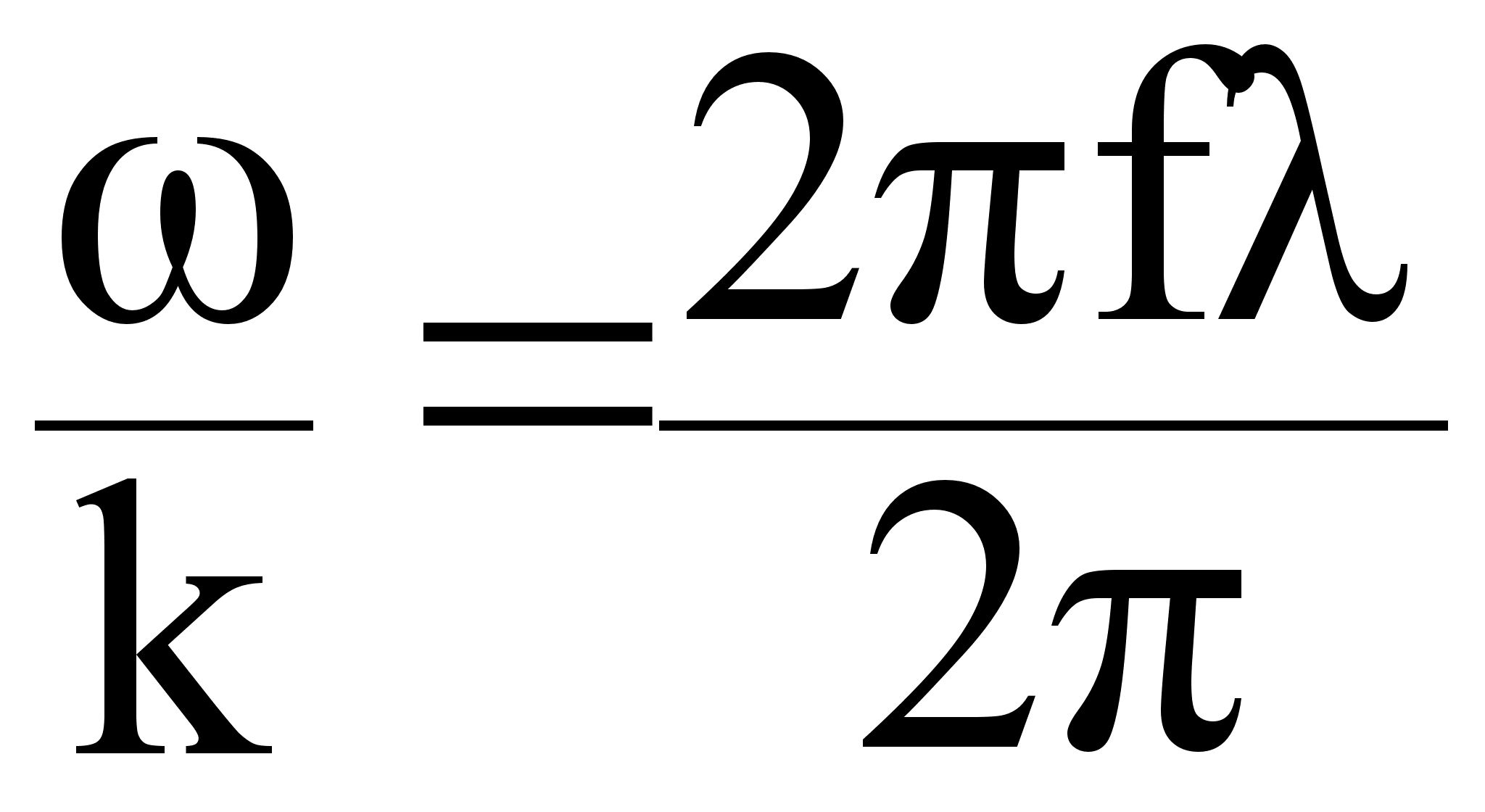 = f если в вакууме, то
= f если в вакууме, то
Vф = c
Vф = f (7.2.12.)
Выясним связь напряженностей Е и Н в ЭМВ:
rot H = j a E
rot E = - j a H
Спроектируем уравнение на оси координат:
![]()
![]() . . .
. . .
i j k
rot H = ![]()
![]()
![]()
Hx Hy Hz
-( ) = ja Ex
) = ja Ex
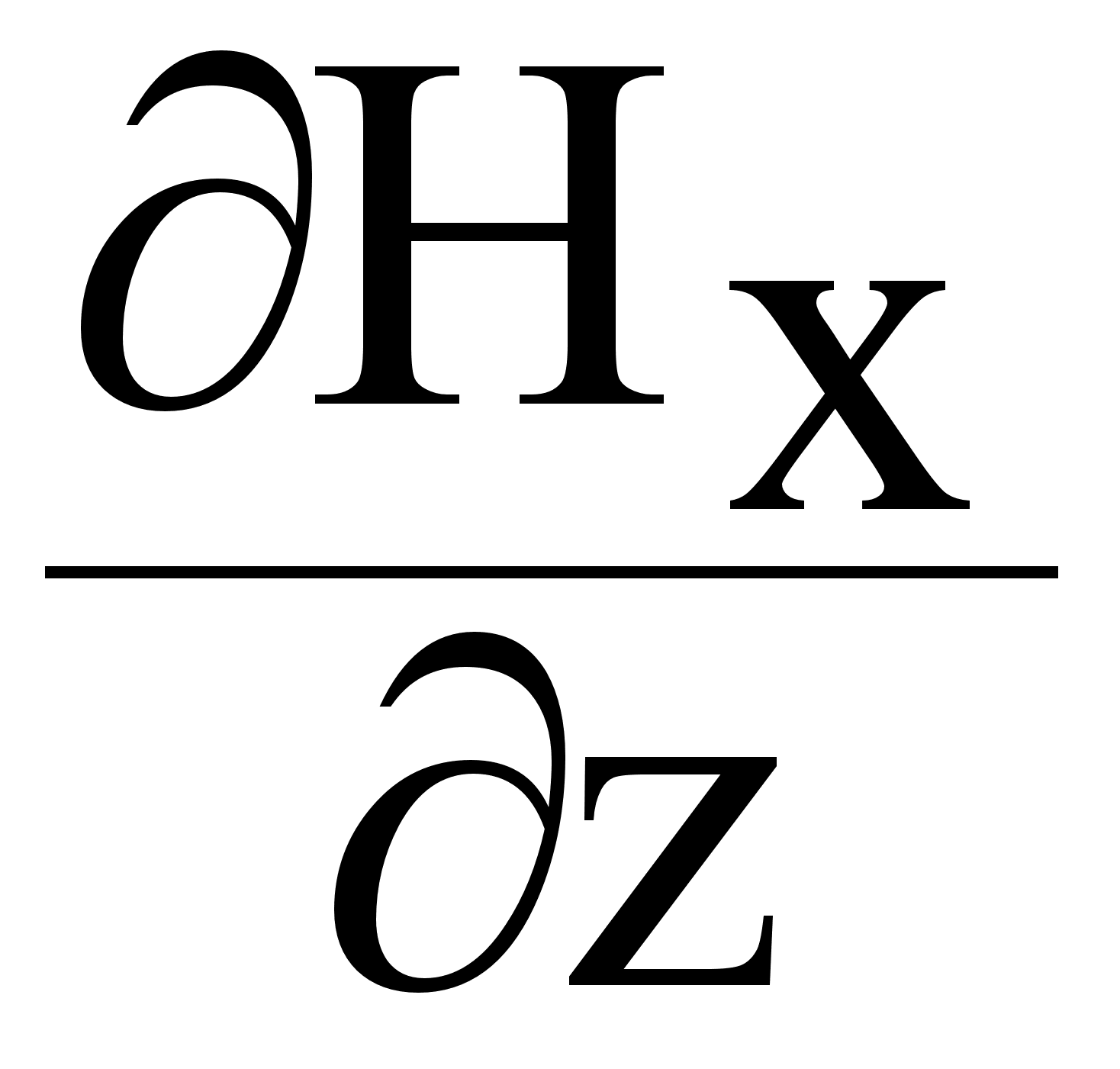 = ja E;
= ja E; 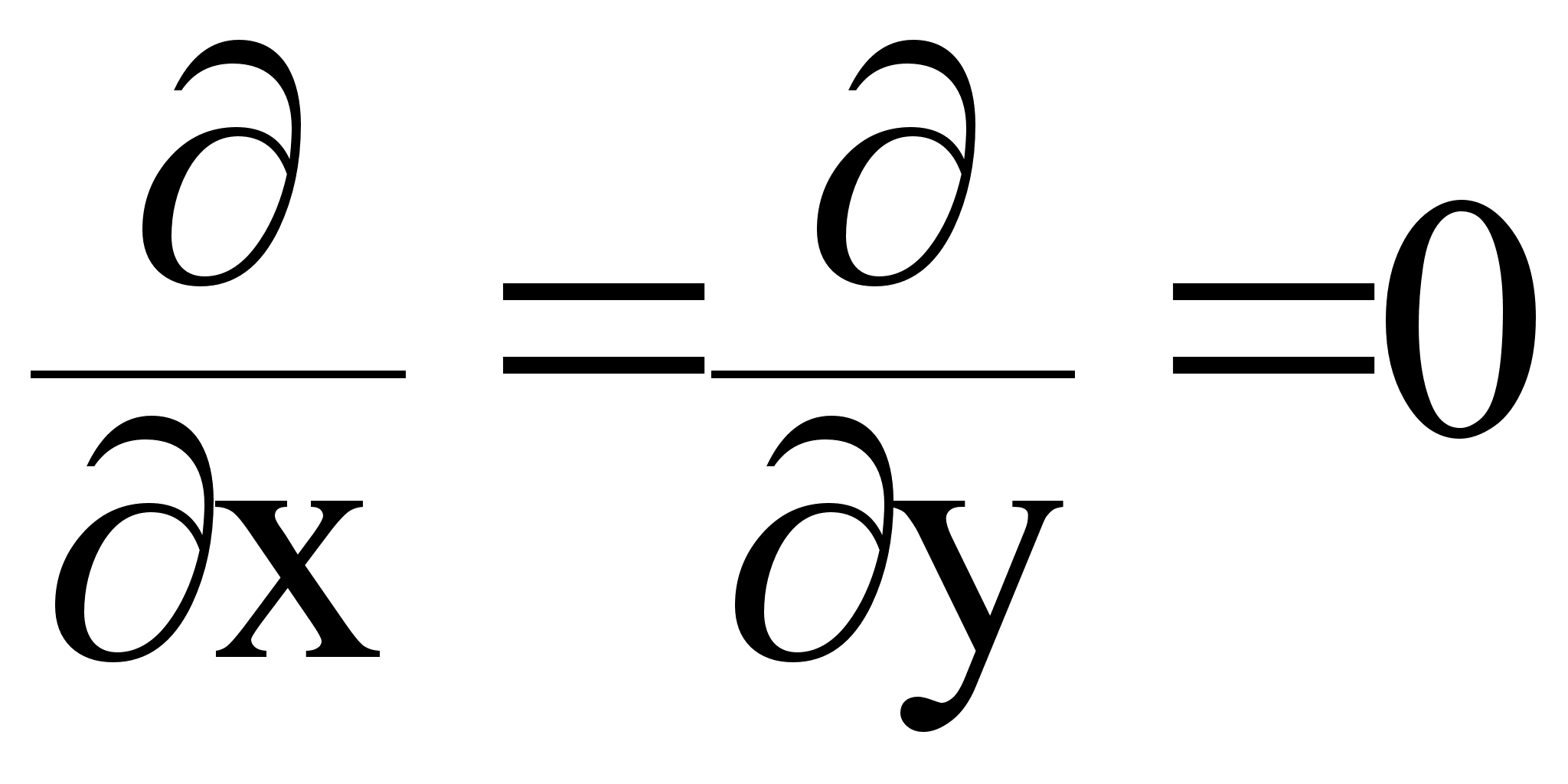
0 = ja Ez
Ez = 0
-( ) = - ja Hx , 0 = - jaHz
) = - ja Hx , 0 = - jaHz
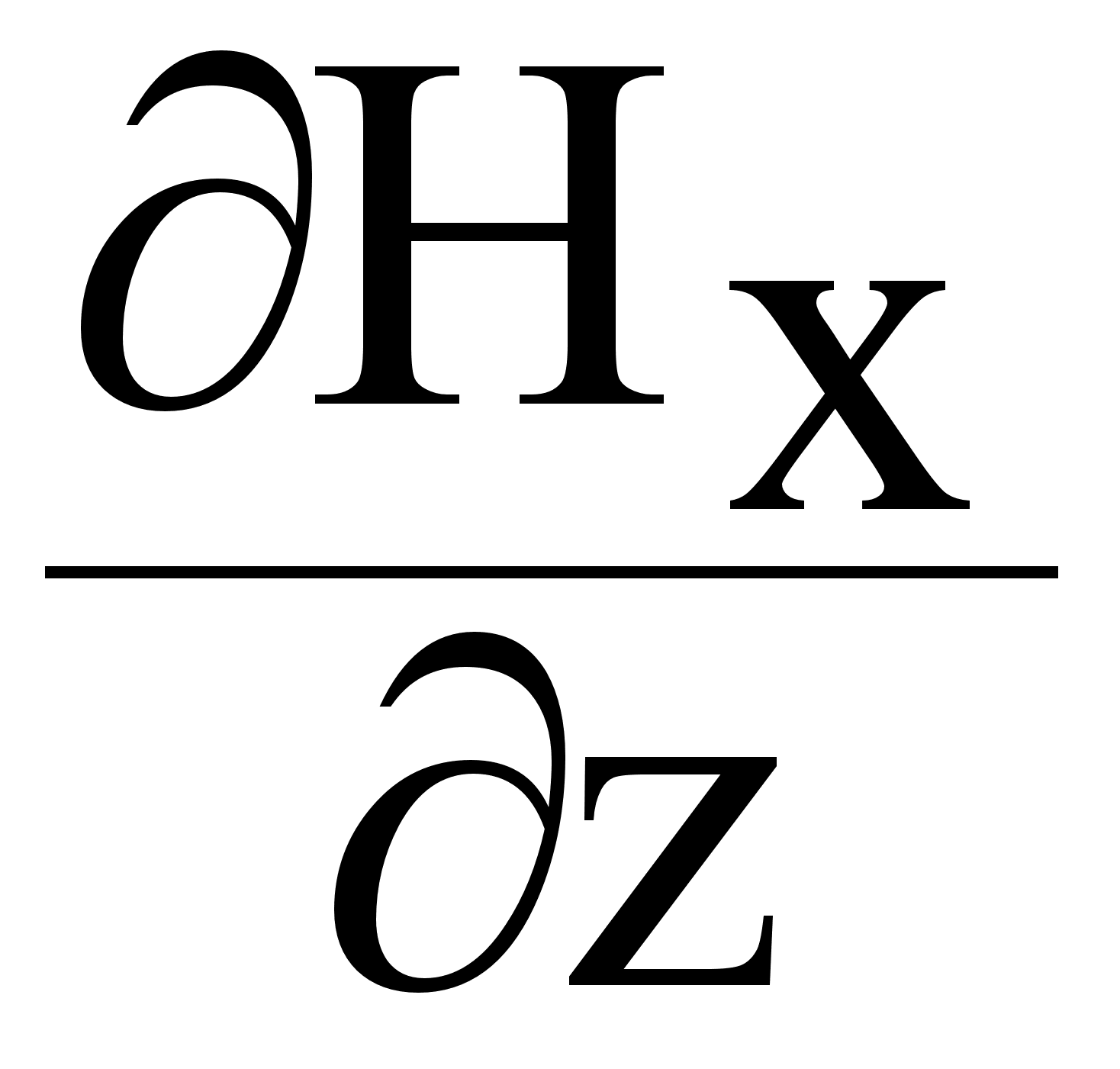 = - j a Hy , Hz = 0 (7.2.13.)
= - j a Hy , Hz = 0 (7.2.13.)
В ЭМВ отличны от нуля только две составляющие в плоскости плоскости распространения:
-( ) = jaEx
) = jaEx
j k Hy = ja Ey
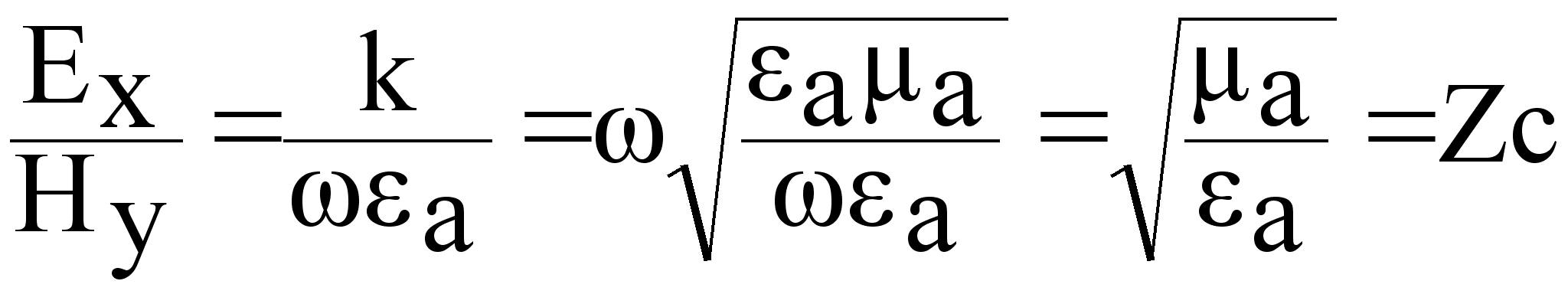 (7.2.14.)
(7.2.14.)
Это лишний раз подчеркивает, что сферические волны излучателя в дальней зоне превращаются в плоские ЭМВ.
Ориентация векторов Е и Н.
Для плоской ЭМВ Е всегда Н.
Покажем, что величина Е Н = 0:
E H = E H cos (E H) = 0
(i Ex + j Ey) (i Hx + j Hy)
ExHx + EyHy = Zc HyHx - ZcHxHy = 0
Ex = Zc Hy ; Ey = - Zc Hx
E H всегда в плоской ЭМВ
H = y0 A e j(t-kz) общая запись
плоской ЭМВ.
H = x0 A Zc e j(t-kz) (7.2.15.)
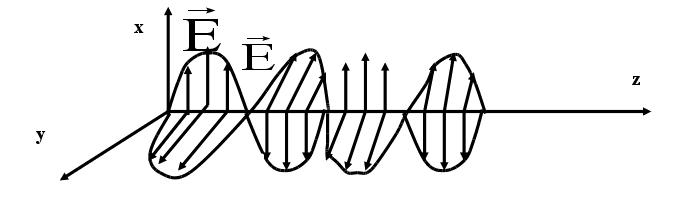
Поскольку в рассматриваемой задаче рассматривается только один источник, то учитываем только волну с амплитудой А. В пространстве имеются
2 взаимно перпендикулярных поля ( Е и Н). Как определить направление переноса энергии ?

![]()
Пср = (![]() ) Re (E H*)
) Re (E H*)
Итоги:
Составляющие Е и Н лежат в плоскости перпендикулярной направлению распространения и изменяются в фазе (там где max Е там max Н, и наоборот)
Отношение
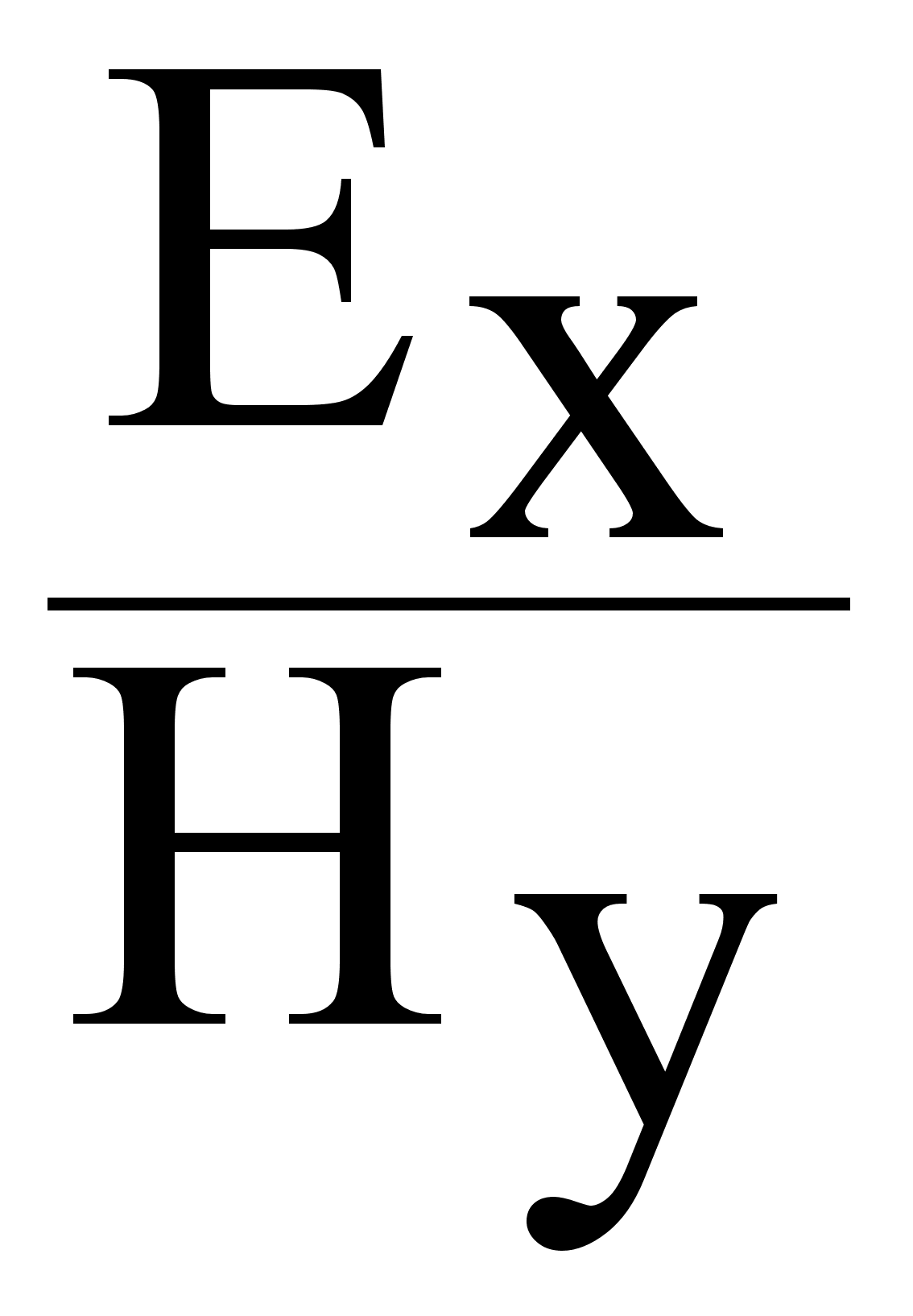 = Zc определенная величина в случае вакуума Zc = 120 . Плоская ЭМВ однородная.
= Zc определенная величина в случае вакуума Zc = 120 . Плоская ЭМВ однородная.Амплитуды Е и Н не зависят от поперечных координат.
У плоской ЭМВ Ez = 0 , Hz = 0.
7.3. Плоские волны в реальных средах.
Предыдущий анализ относился к идеальным средам. В реальных средах часть энергии будет теряться в среде, значит амплитуда волны будет убывать. Любая реальная среда - набор связанных зарядов (диполей), могут быть и свободные заряды.

Часть энергии переходит в тепло. Количественно опишем процесс.
В реальных средах, при гармонических воздействиях проницаемости величины комплексные:
= `a - j a``
= a` - j a`` (7.3.1.)
Все рассуждения и результаты сохраняют силы, но параметры аа - комплексные.
Амплитудные соотношения.
С этой целью рассмотрим, что представляет собой волновое число в реальной среде:
____ _________________
k = aa = (a`- ja``)(a`- ja``) = - j (7.3.1.)
поскольку величины а и а - комплексные, то k - тоже величина комплексная. К каким последствиям это может привести ? Рассмотрим волновой процесс:
H (z,t) = y0 A e j(t-kz) = y0 A e t-(jz) =
 = y0 A e ej(t- (7.3.3.)
= y0 A e ej(t- (7.3.3.)
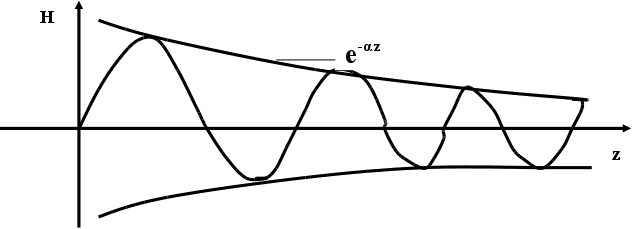
Параметр получил название коэффициента затухания. - фазовая постоянная - вещественная часть волнового числа.
Vф = / в реальных средах 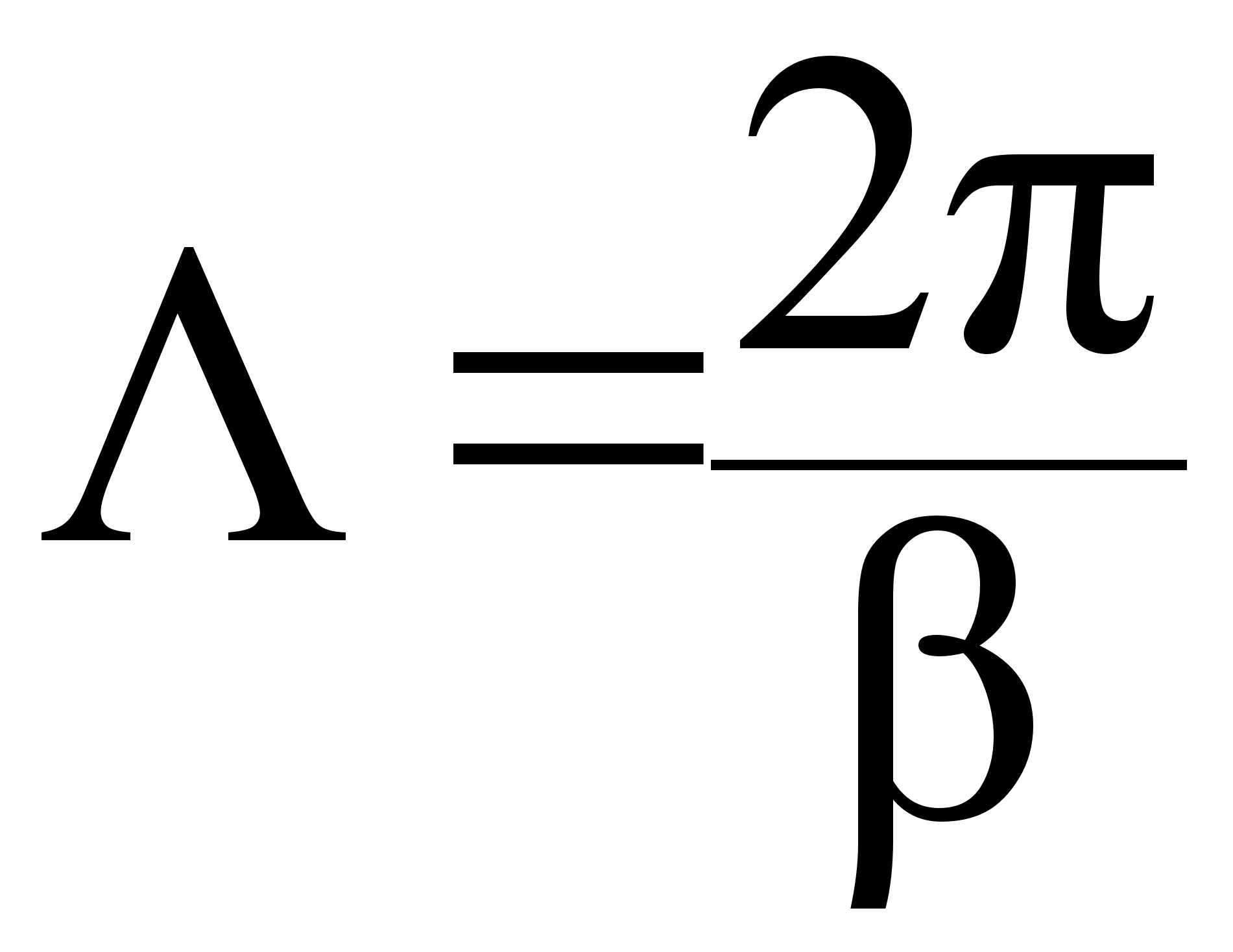 (7.3.4.)
(7.3.4.)
Понятие было введено для идеального диэлектрика. Если затухание мало, то можно выбрать точки, где поля отличаются по фазе на 2 и считать, что это . Если затухание очень велико, периодичность процесса теряет смысл (соленая вода), понятием можно пользоваться условно.
Количественная оценка.
Рассмотрим поведение амплитуды в точках:
в т. Z1 H(Z1) = A e - 1
в т. Z2 H(Z2) = A e - 2
Изменение
a = 20 lg (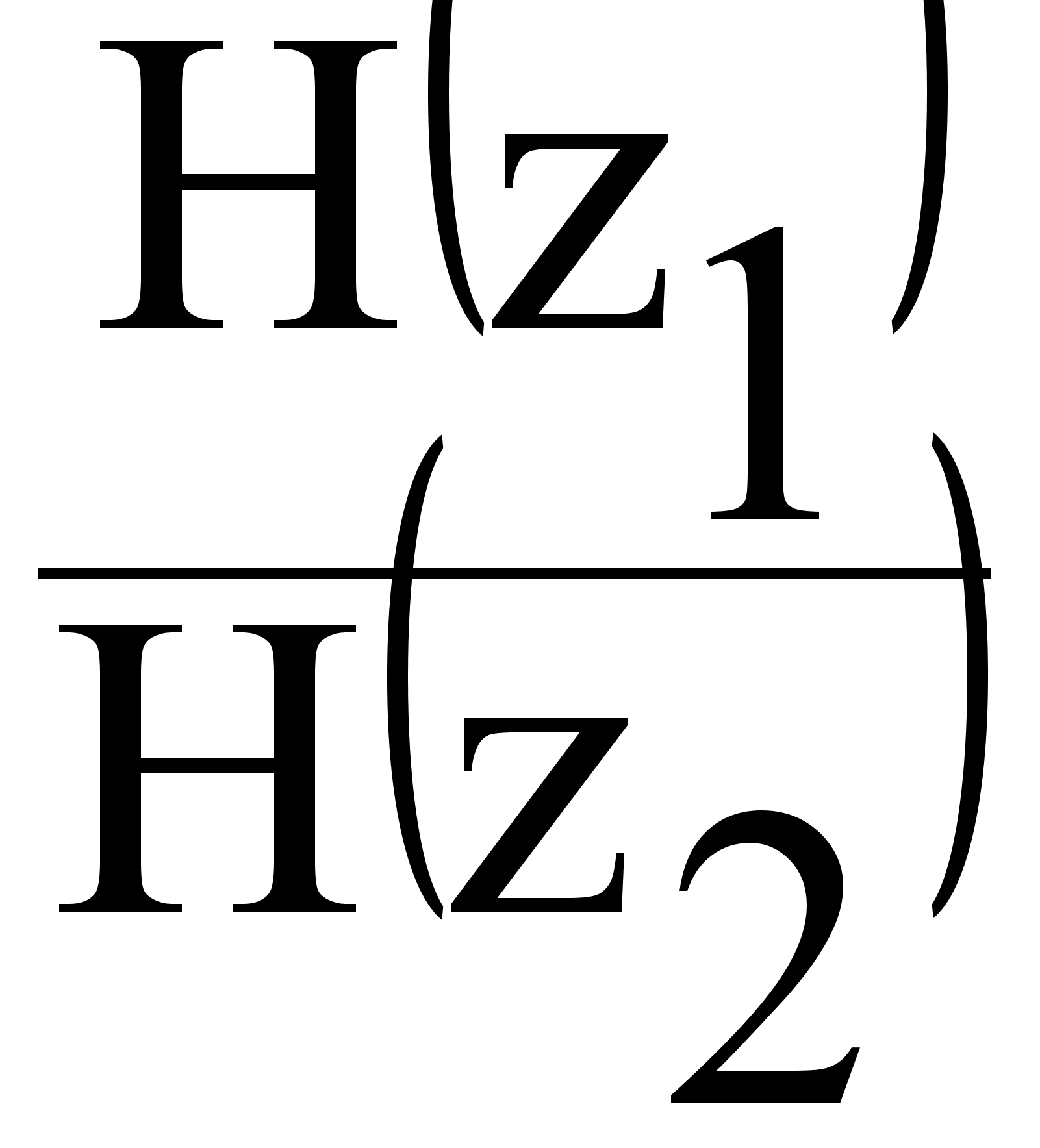 ) = 20 lg (
) = 20 lg (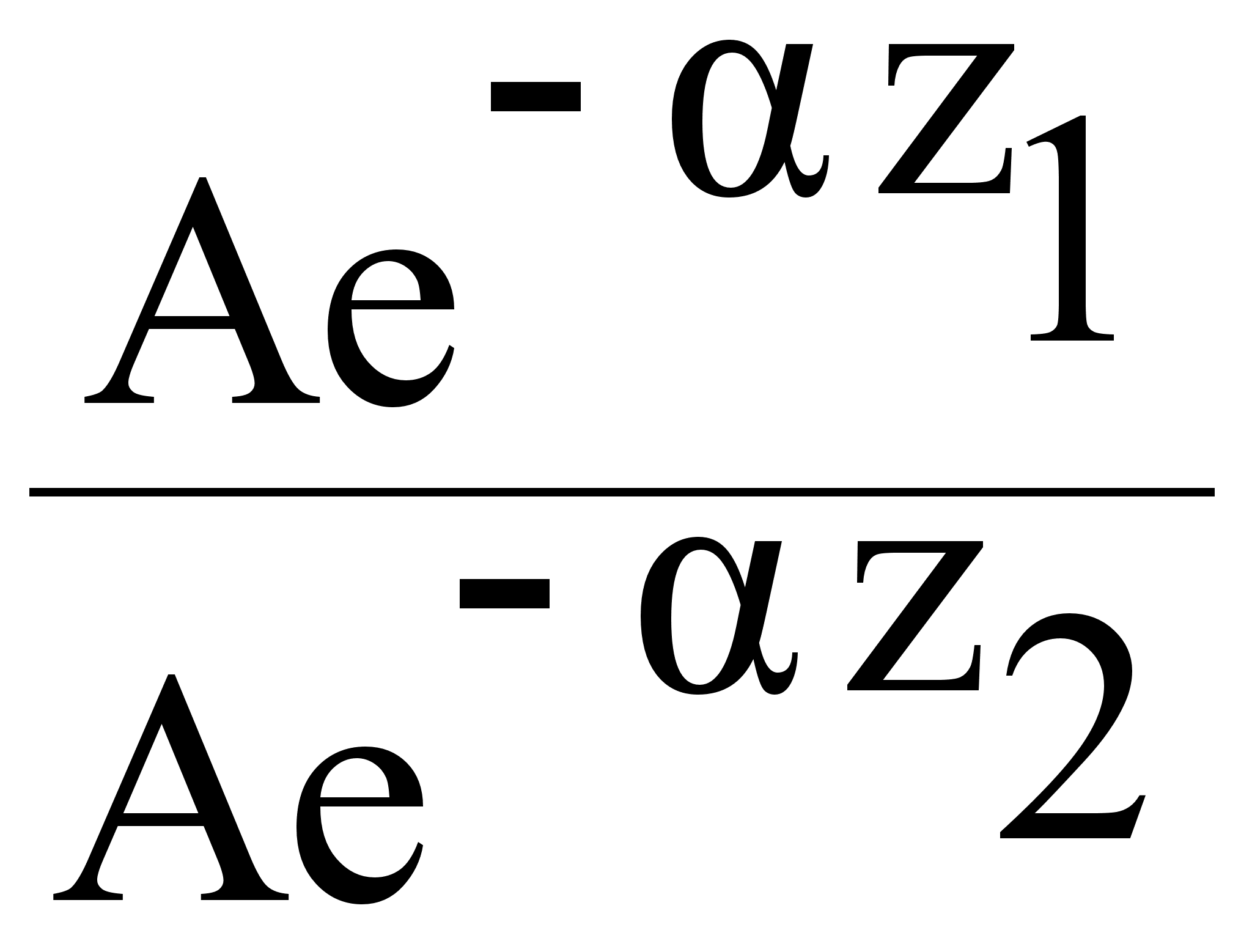 ) =
) =
= 20 lg e 2- 1 = 20 (Z2 - Z1) lg ℓ
Z2 - Z1 = ℓ
a = 8,69 l (дБ) (7.3.5.)
во столько раз, пересчитанных в дБ уменьшилась амплитуда поля .
Под глубиной проникновения поля понимают расстояние, на котором амплитуда поля убывает в е раз
(вектор Е и Н).
Изменение поля Н = A e - . На расстоянии равном глубине проникновения в точке Z = 0, Н1 = А
в т. Z = 0 H2 = A e -
![]() = е = е - ; 0 = 1
= е = е - ; 0 = 1
0 = ![]() (7.3.6.)
(7.3.6.)
Фазовые соотношения
Воспользуемся понятием “характеристическое сопротивление cреды”
____ ________________
Zc = ![]() = a` - ja``/ a`- ja``=Zc ej (7.3.7.)
= a` - ja``/ a`- ja``=Zc ej (7.3.7.)
в реальных средах Zc величина комплексная. Поведение
Е и Н в реальной среде:
H(z,t) = y0 A e - e j(t-
E(z,t) = x0 A Zc e - e j(t- =
= x0 A Zce - e j(t- (7.3.8.)
Модуль характеристического сопротивления означает отношение амплитуд между электрическим и магнитным полями, а фаза характеристического сопротивления показывает величину сдвига фаз между
Е и Н. В реальных средах всегда Е и Н сдвинуты на некоторую величину.
Волновой процесс в реальных средах
![]()
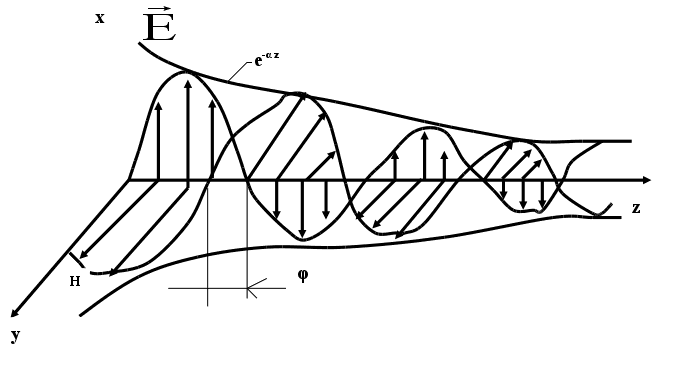
Расчет коэффициента затухания и
фазовой постоянной в реальной среде
Проведем расчет для частного случая, широко используемого на практике.
Реальная cреда не магнитный диэлектрик.
a = a`- ja`` ; a = a`- j0 = (7.3.9.)
(почва, вода)
Порядок расчета:
1) Из общих выражений для k:
____________
k = - j = (a`- ja``) a` (7.3.10.)
Выделим вещественную и мнимую часть. Для этого левую и правую часть возведем в квадрат, т.к. надо избавиться от радикалов:
2 - 2 j - 2 = 2a`a ` - j2a``a`
Два комплексных числа тогда равны, когда равны и вещественные и мнимые части.
2 - 2 = 2a`a`
2 = 2a``a`
2a`a` = q - обозначим
2a``a` = 2a`a![]() = q tg
= q tg
![]() = tg (7.3.11)
= tg (7.3.11)
2 - 2 = q ; = 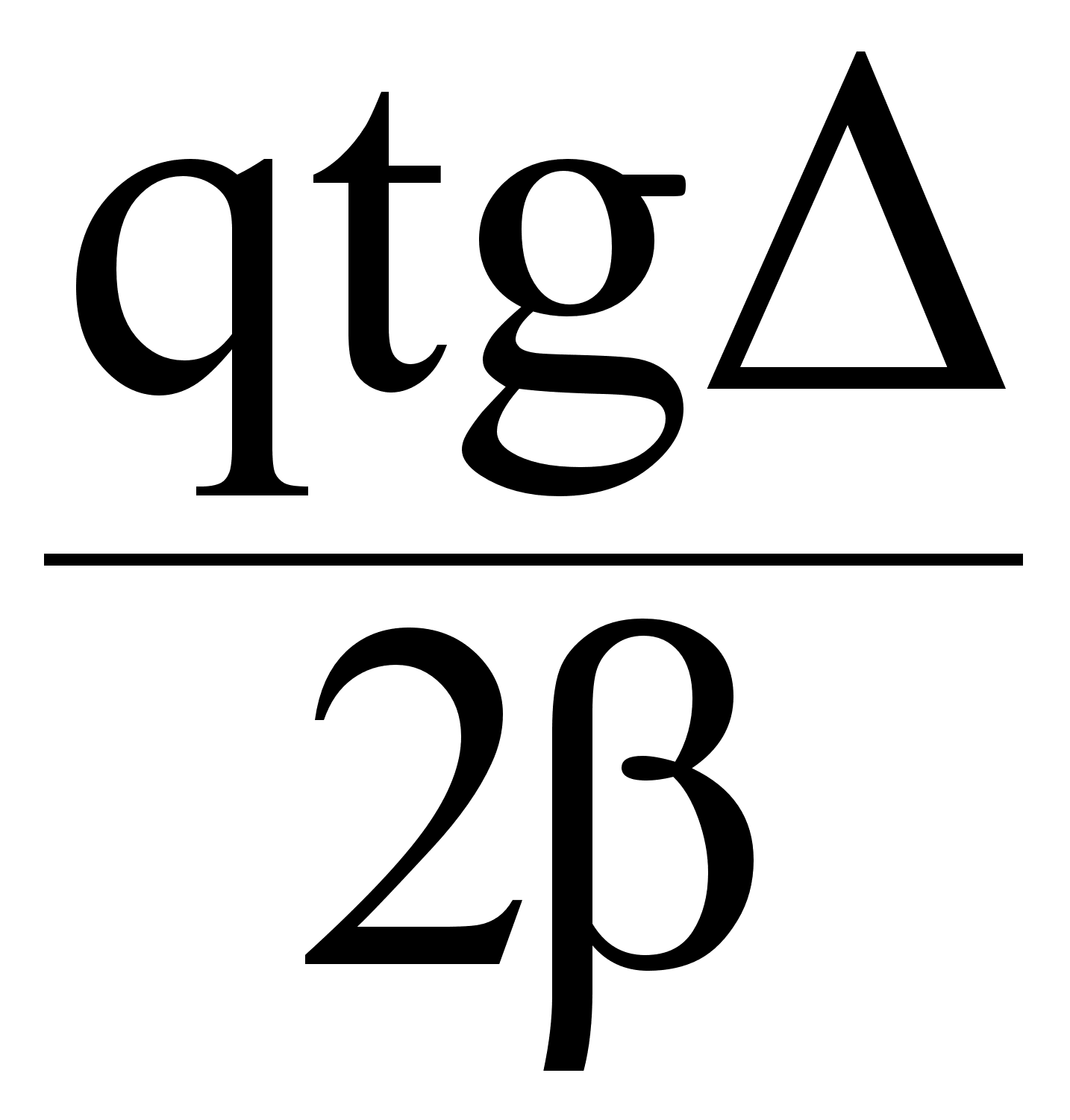
2 = q tg
2 - (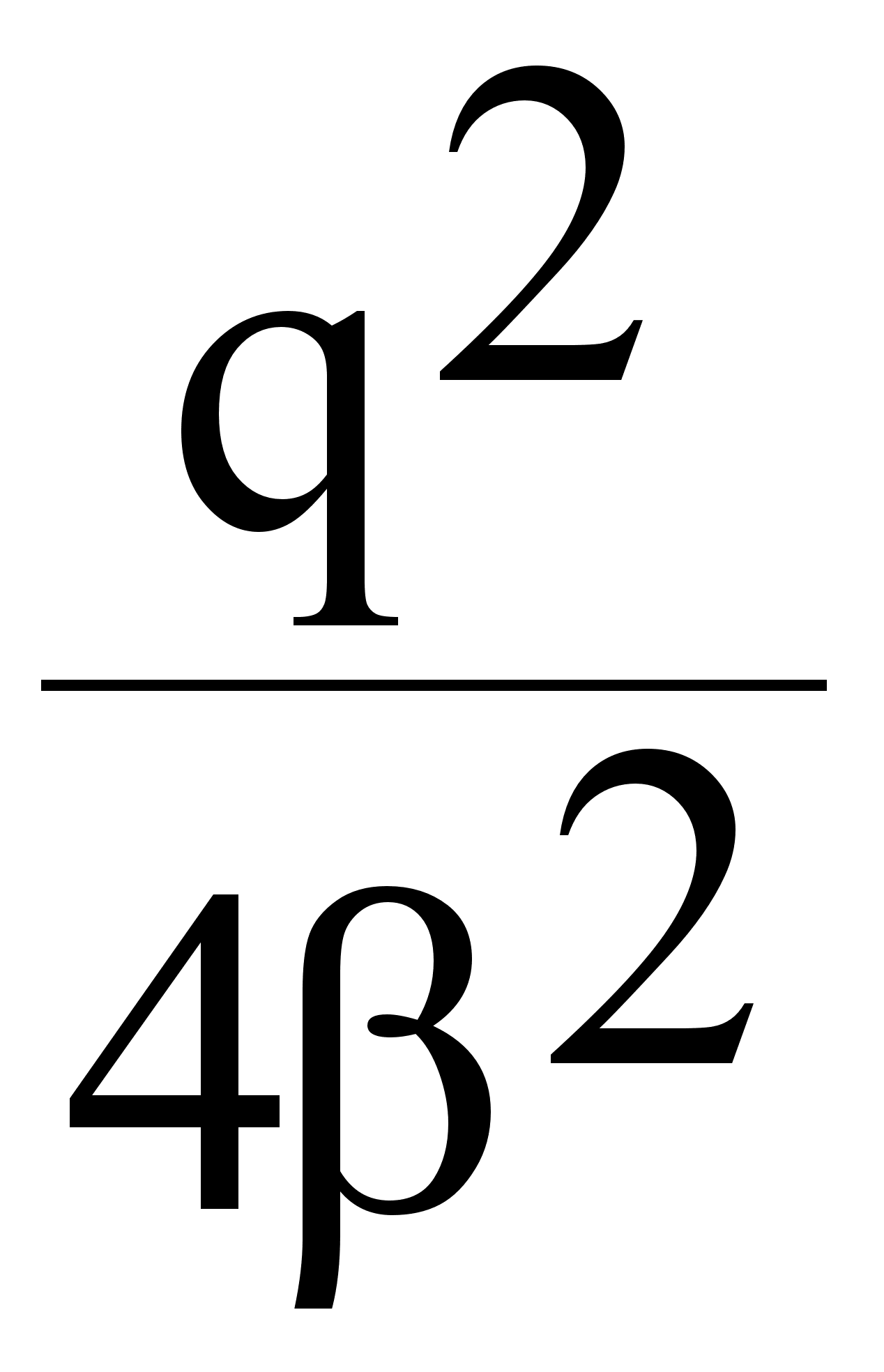 ) tg2 - q = 0
) tg2 - q = 0
4 - q2 - (![]() ) tg2 = 0
) tg2 = 0
2 = 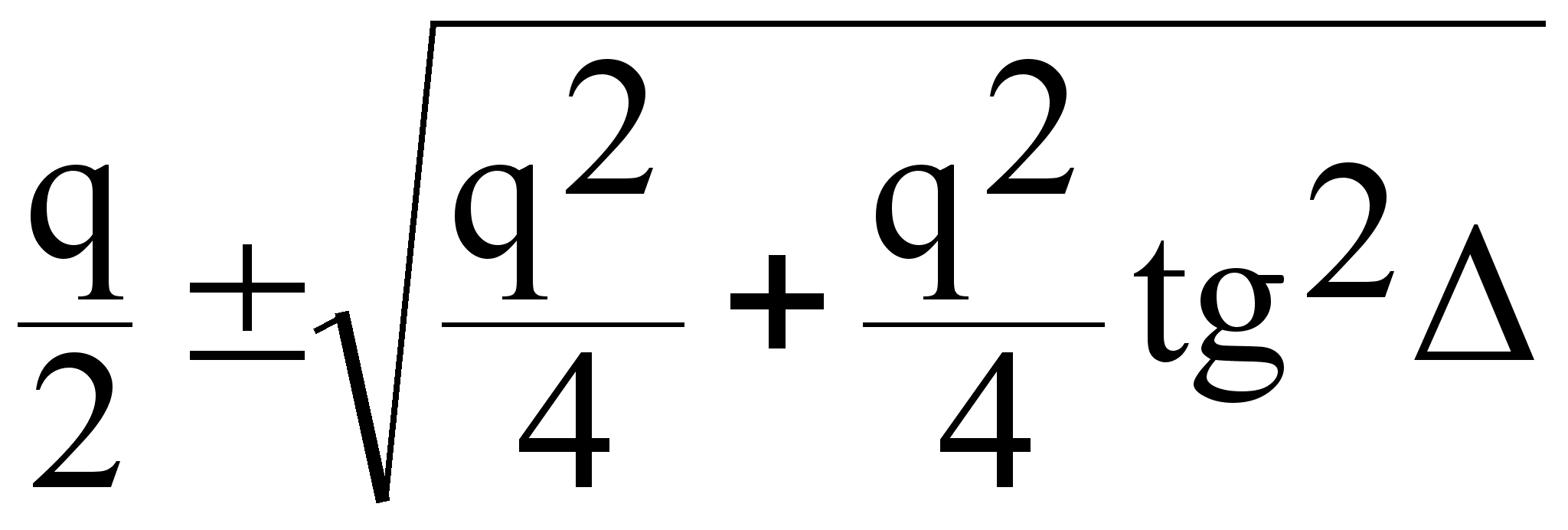
Какой знак взять + или - ?
Исходя из физического смысла оставляем только +, т.к. - будет отрицательная.
2 = ![]() (1 + 1 + tg2)
(1 + 1 + tg2)
![]() =
= 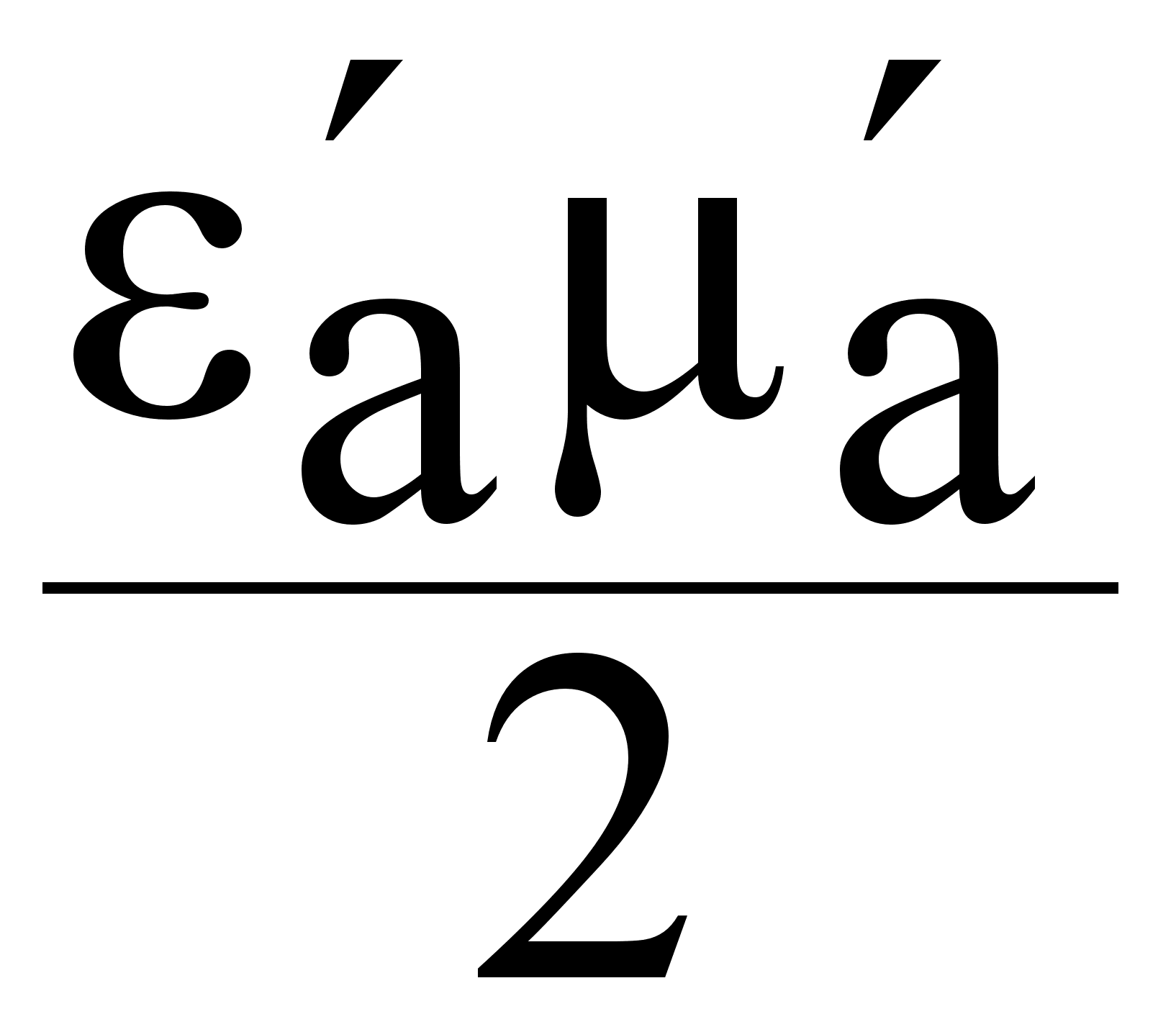 ( 1 + tg2 + 1) (7.3.12)
( 1 + tg2 + 1) (7.3.12)
для решение аналогичное:

= 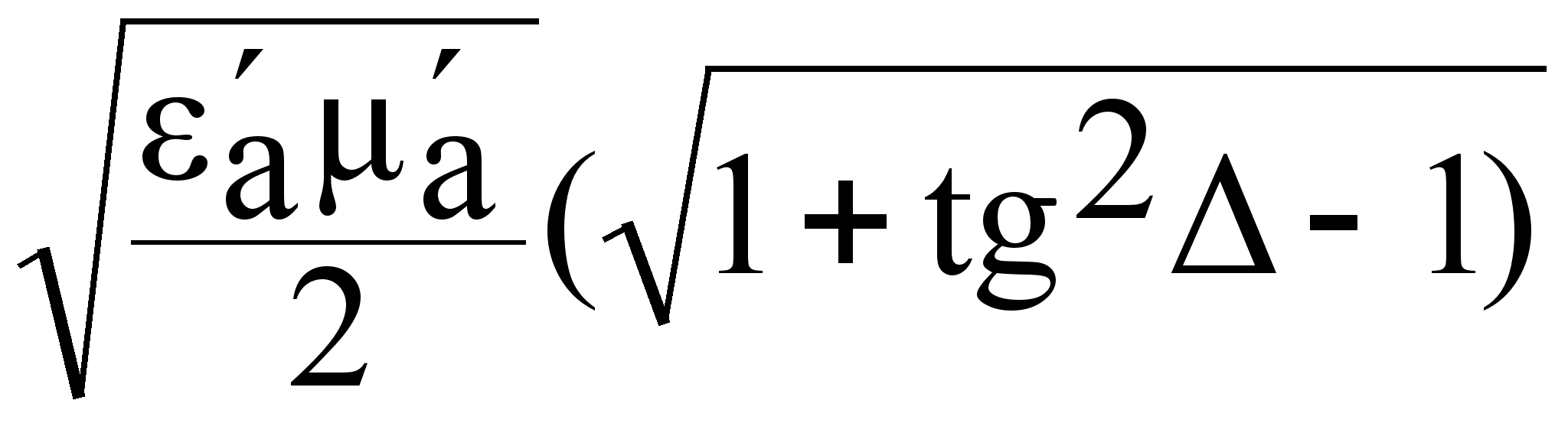 (7.3.13)
(7.3.13)
Выводы:
1. По определению Vф = ![]()
Vф = 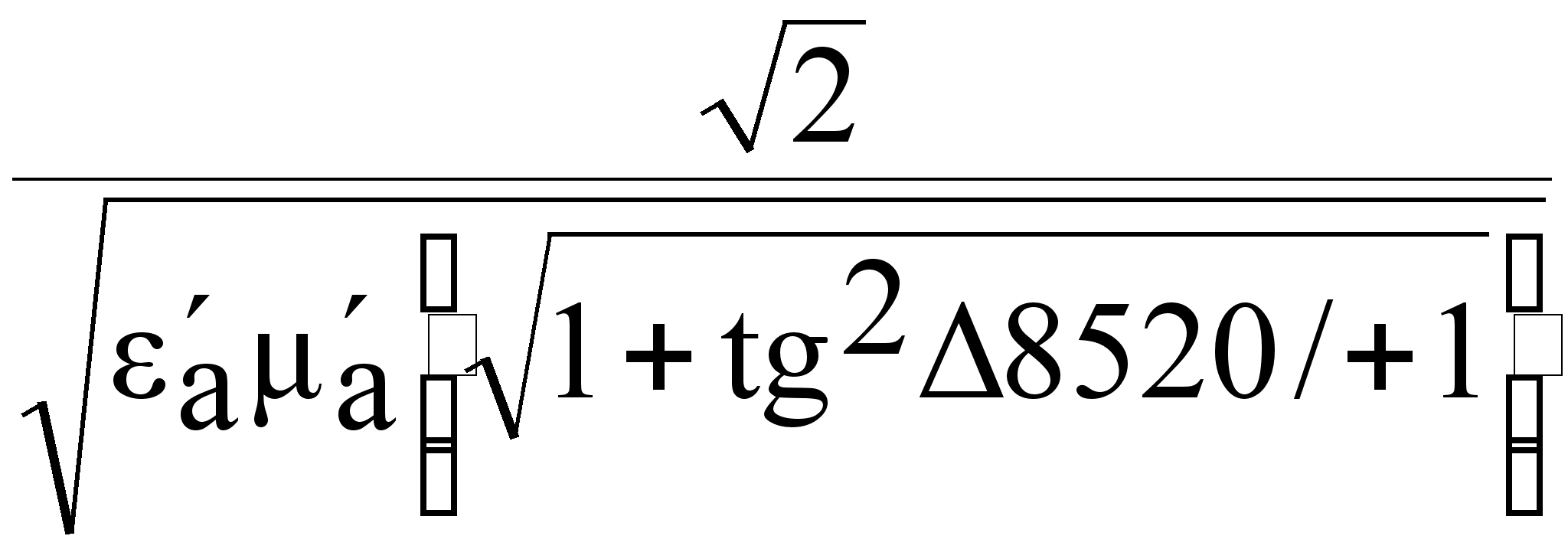
tg = 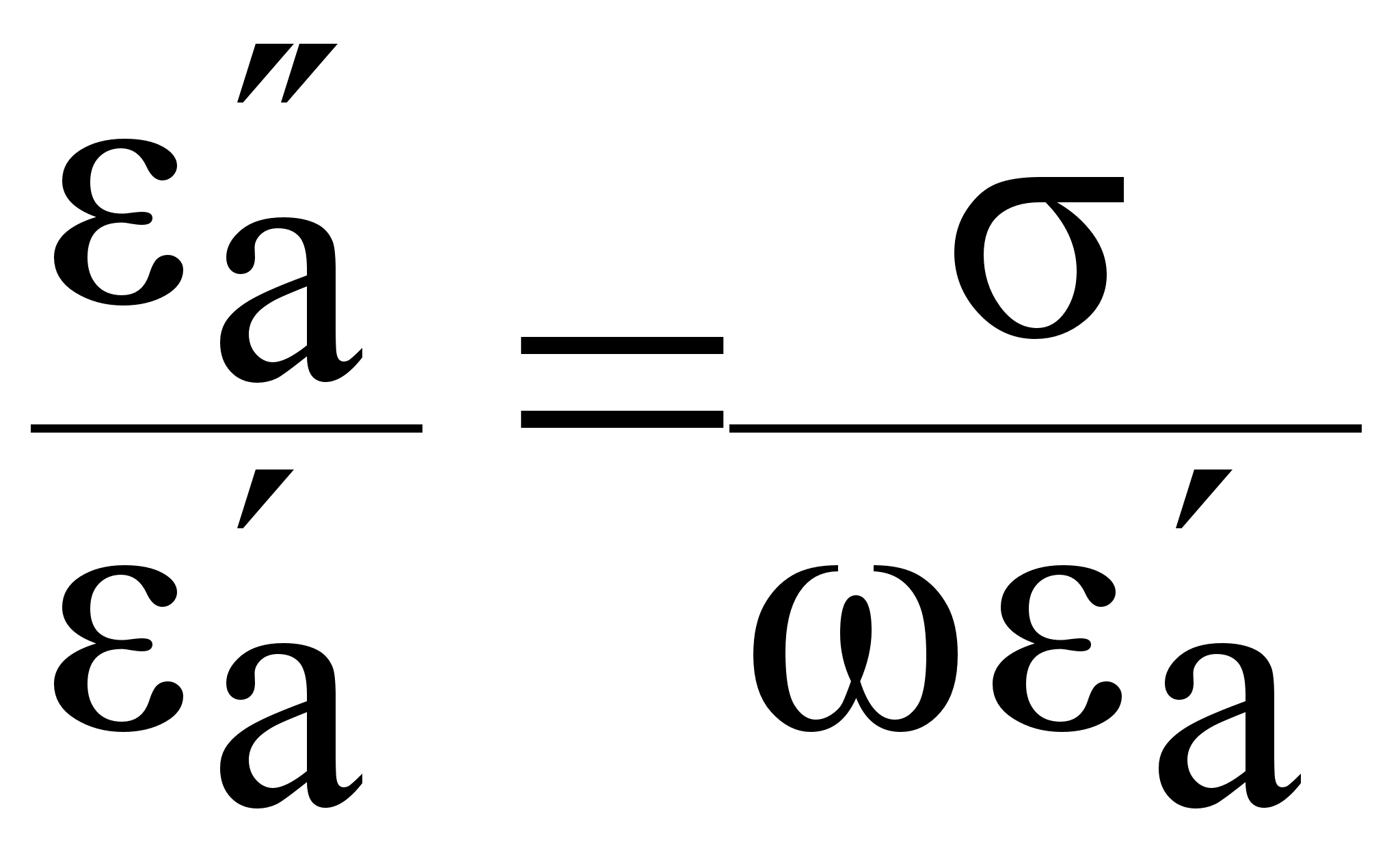
Vф зависит от частоты. Встретились с явлением дисперсии. Зависимость Vф от f называется дисперсией. Идеальная среда не обладает дисперсией.
= 0 - идеальная среда
0 - реальная
Рассмотрим поведение ЭМВ в двух случаях:
1) Среда с малыми потерями, малым затуханием:
tg << 1
 _____
_____
= a`a` (7.3.14.)
совпадает с волновым числом для идеального диэлектрика с параметрами а, а.
Для :
________
1 + tg2 1 + (![]() ) tg2 - разложение в ряд
) tg2 - разложение в ряд
_____
1 + x 1 + x2
![]() =
= 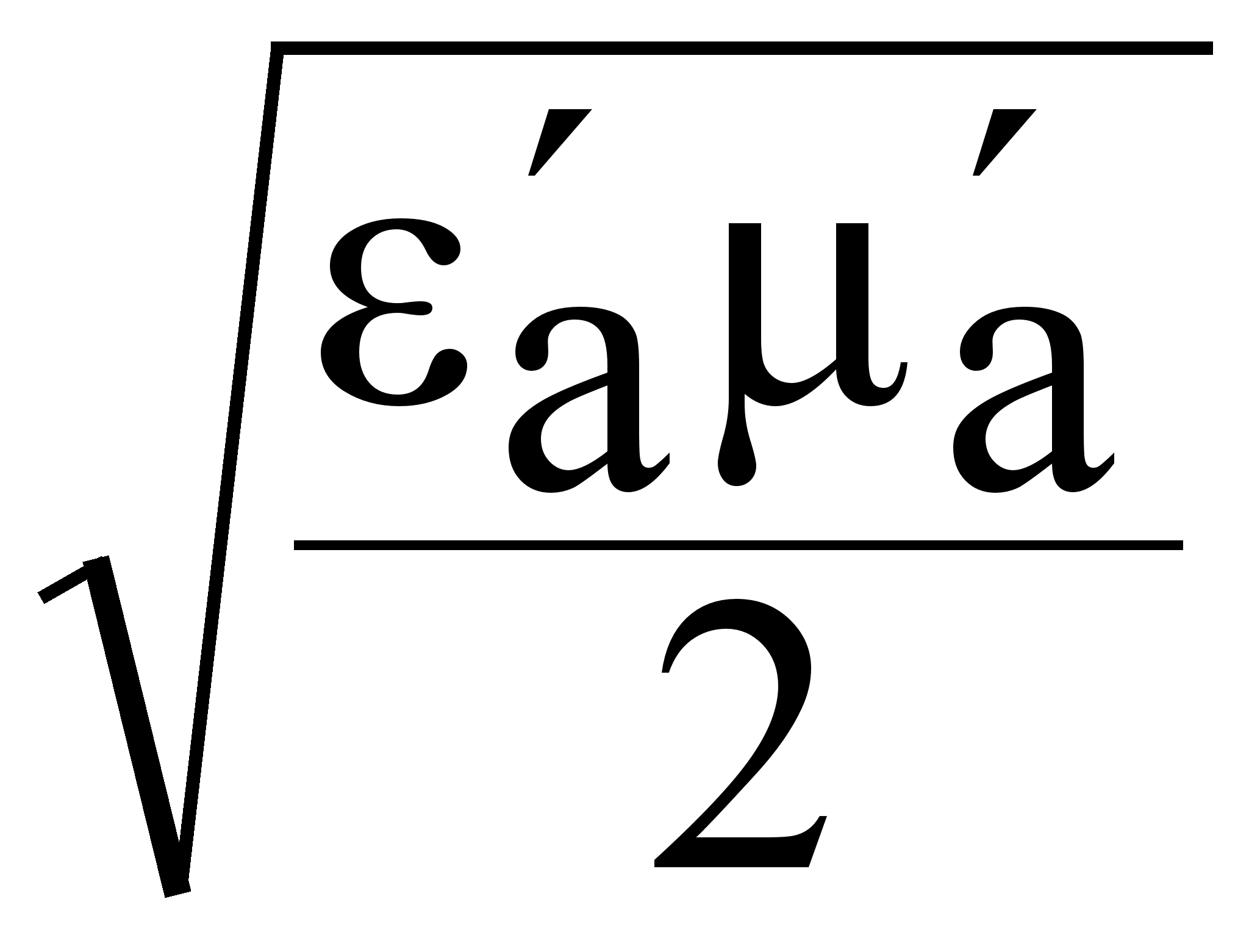 tg =(
tg =(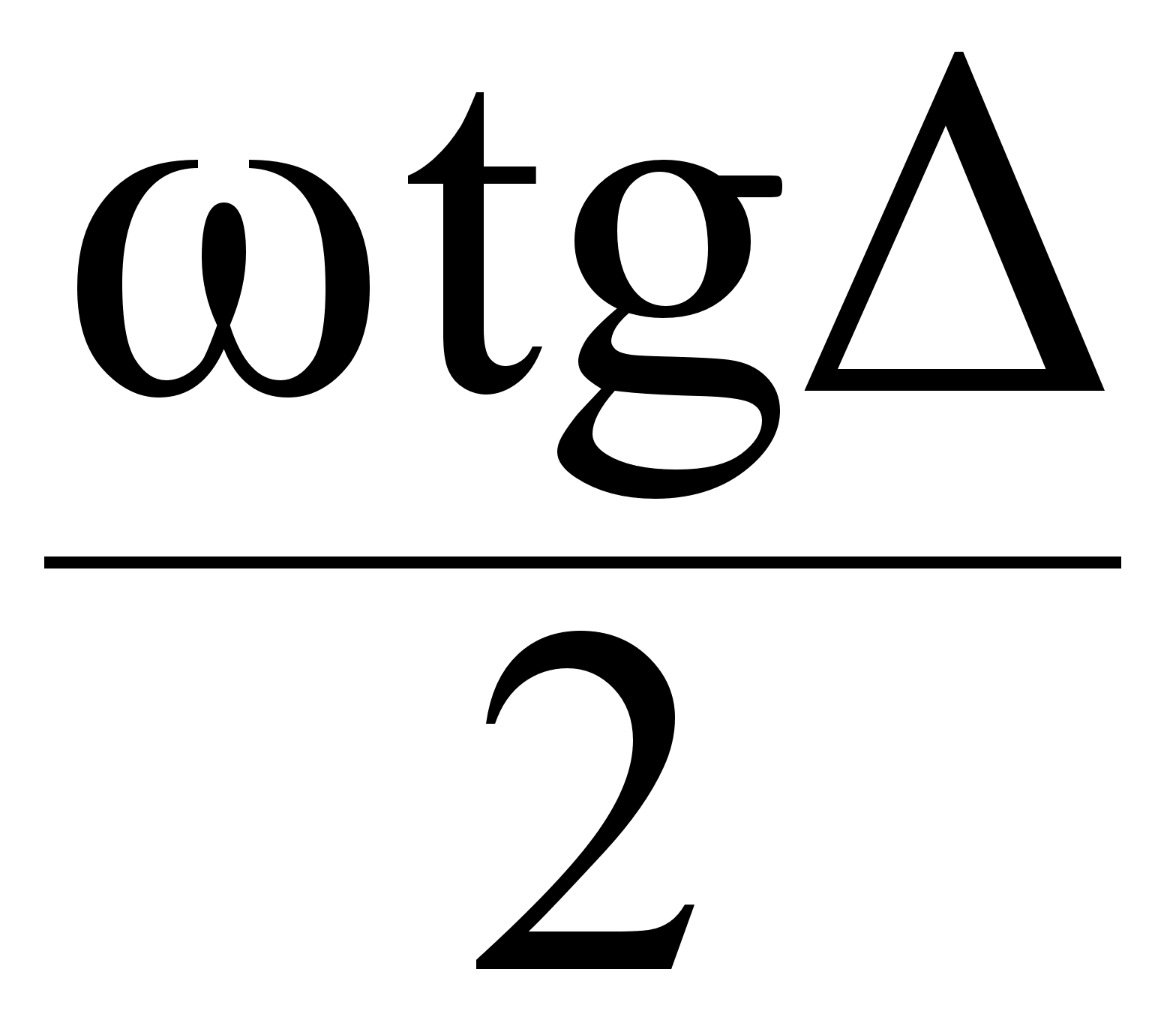 ) a`a`
) a`a`
чем > tg , тем >. (7.3.15)
2) Среда с большими потерями.
tg >> 1
= 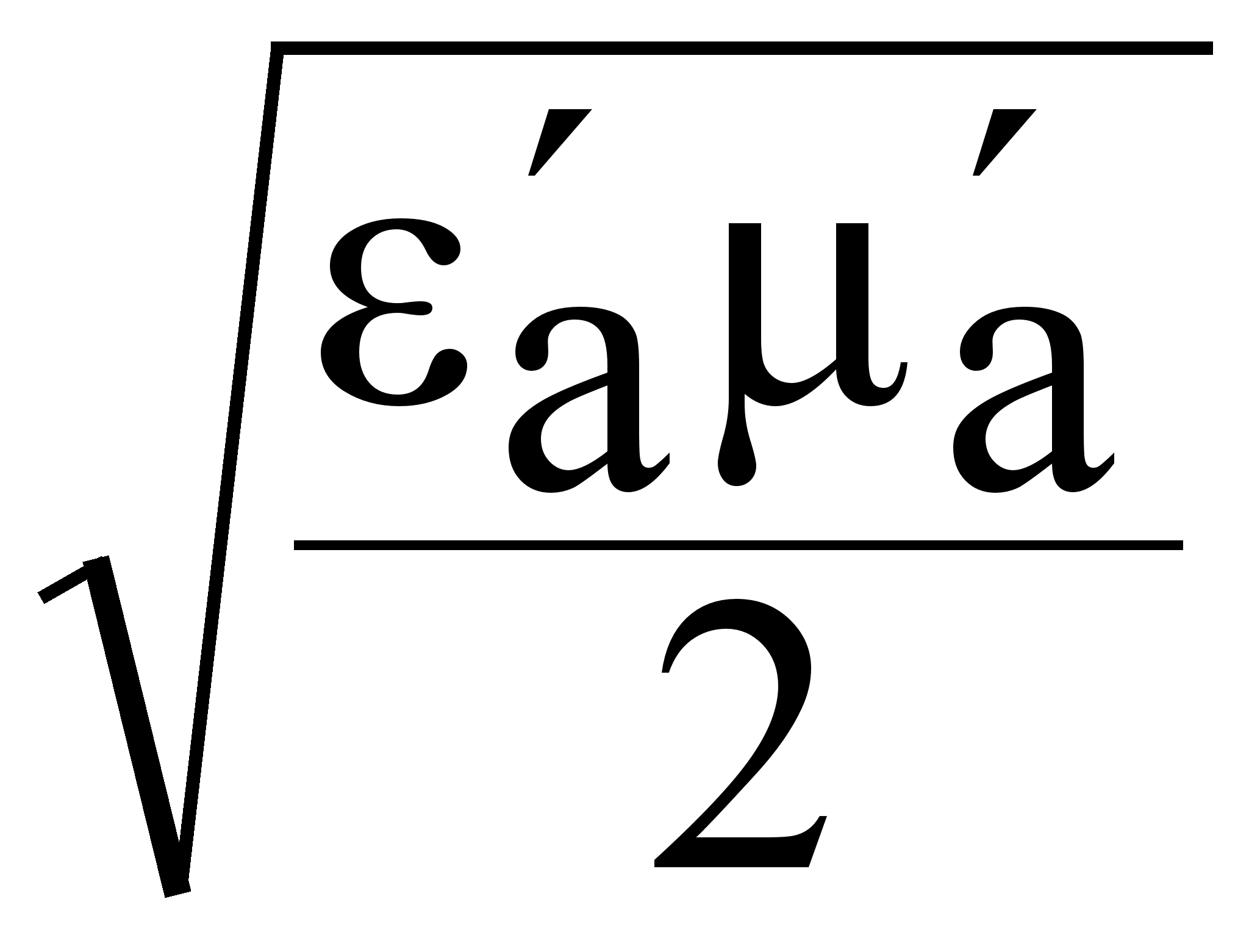 tg
tg
=
= = 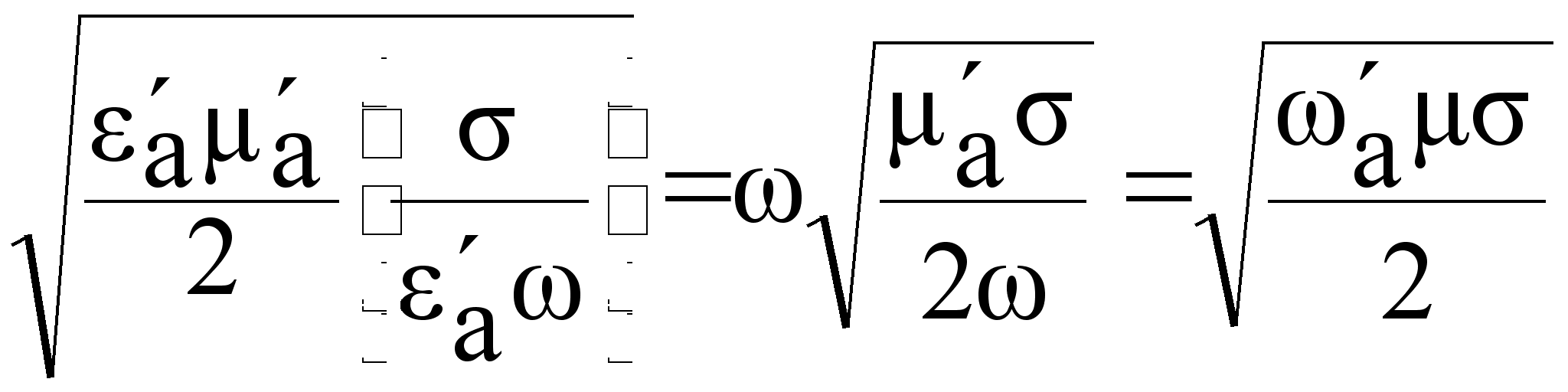

tg = 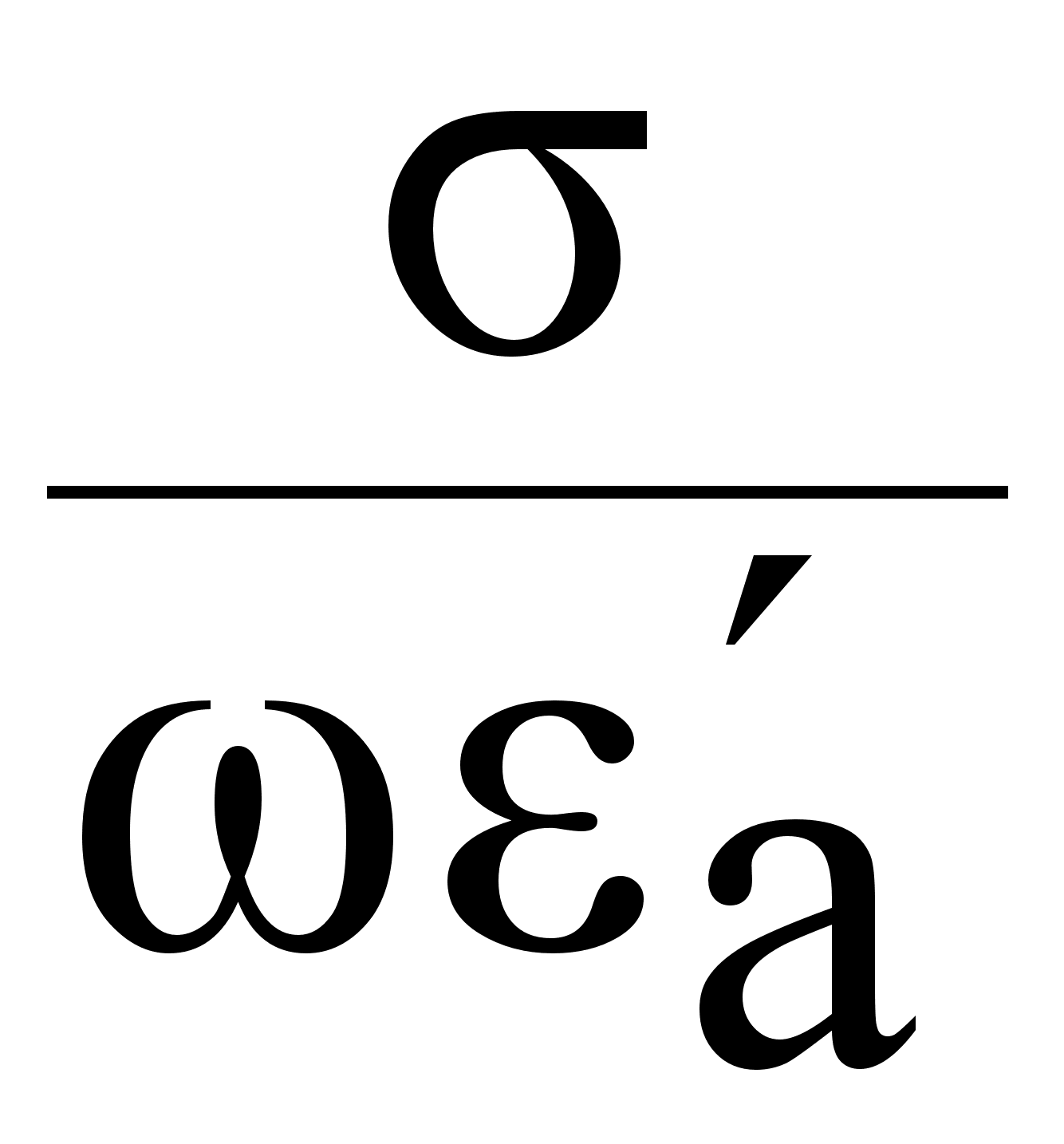
= = 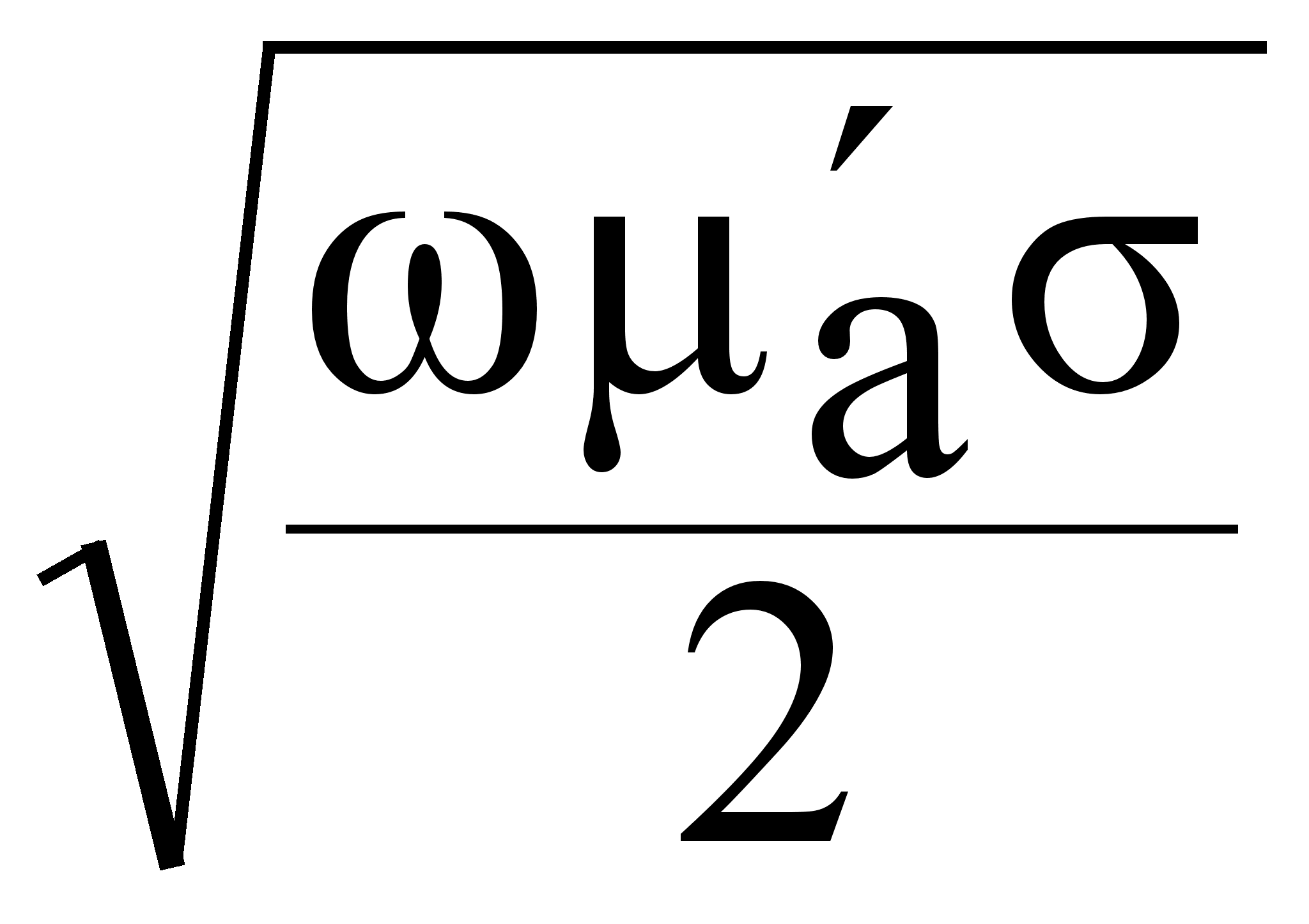 (7.3.16.)
(7.3.16.)
0 = 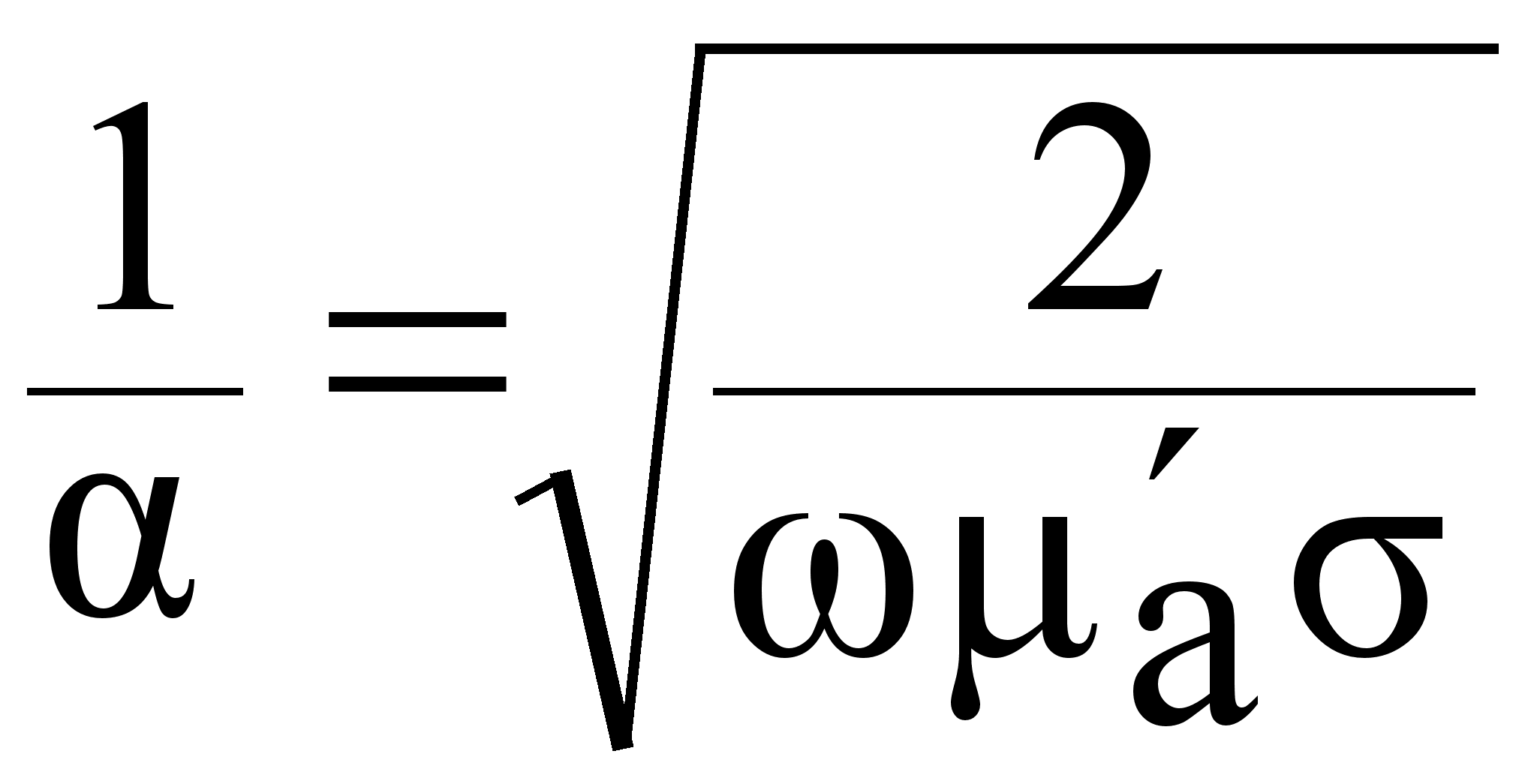
Пример:
Определить во сколько раз уменьшается амплитуда волны на расстоянии равном длине волны (в среде с большими потерями).
e = e = e = e = 540 раз
7.4. Групповая скорость плоских волн
Все реальные сообщения занимают определенный спектр частот и возникает вопрос, какой реальный сигнал передается ?

1 23
В реальных средах, каждая гармоническая составляющая передается со своей скоростью 123. С какой скоростью передается сигнал ?
Рассмотрим простой случай, когда сообщение состоит из двух гармонических сигналов:
1 = A cos (1t - k1 Z)
2 = A cos (2t - k2 Z) (7.4.1.)
Рассмотрим сложение двух сигналов:
= 1 + 2 = A (cos (1t - k1 Z) + cos (2t - k2Z))
= 2A cos ((1 -![]() ) t - (k1 -
) t - (k1 -![]() ) Z) *
) Z) *
*cos ((1 +![]() ) t - (k1 +
) t - (k1 +![]() ) Z)
) Z)
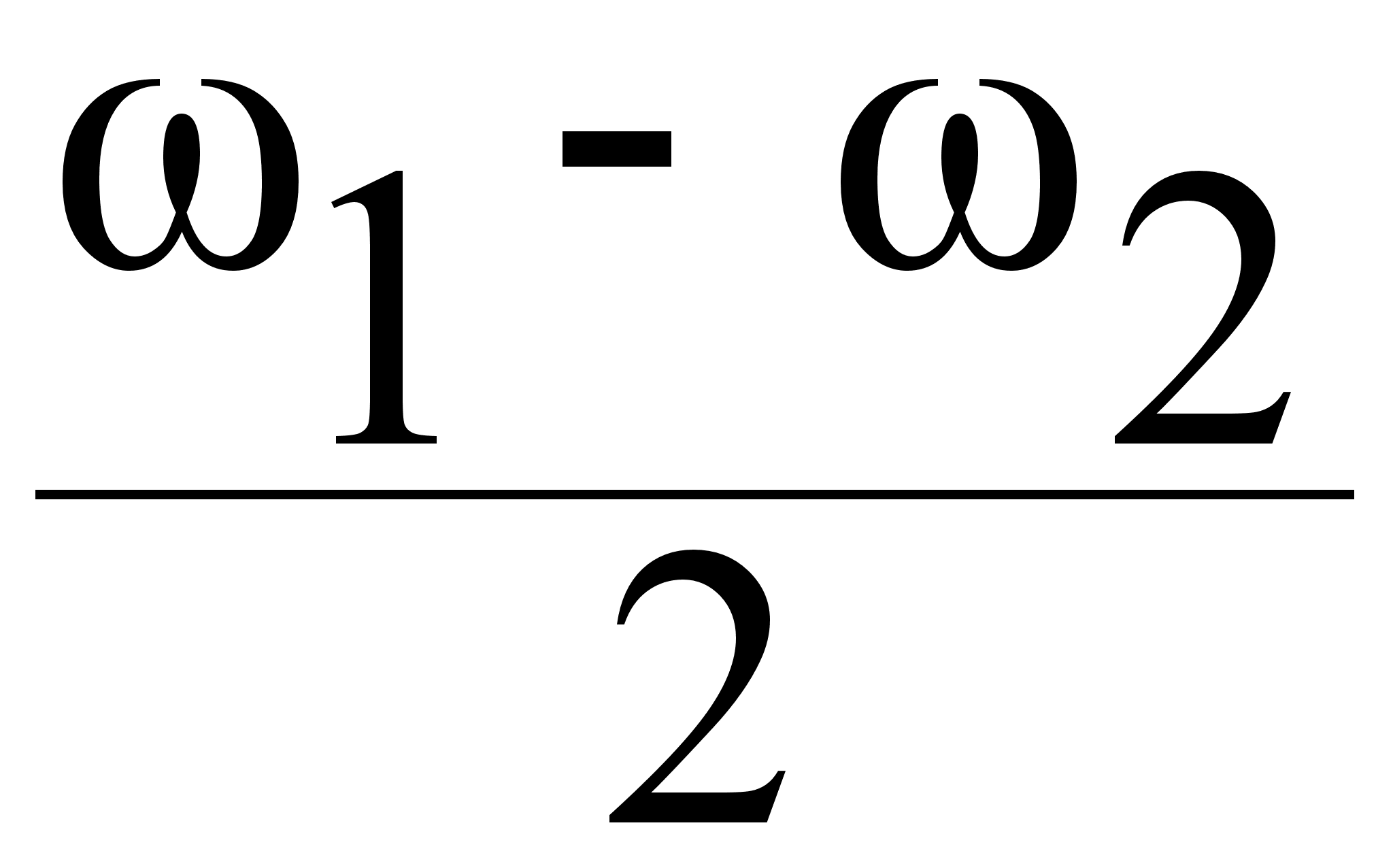 =
= 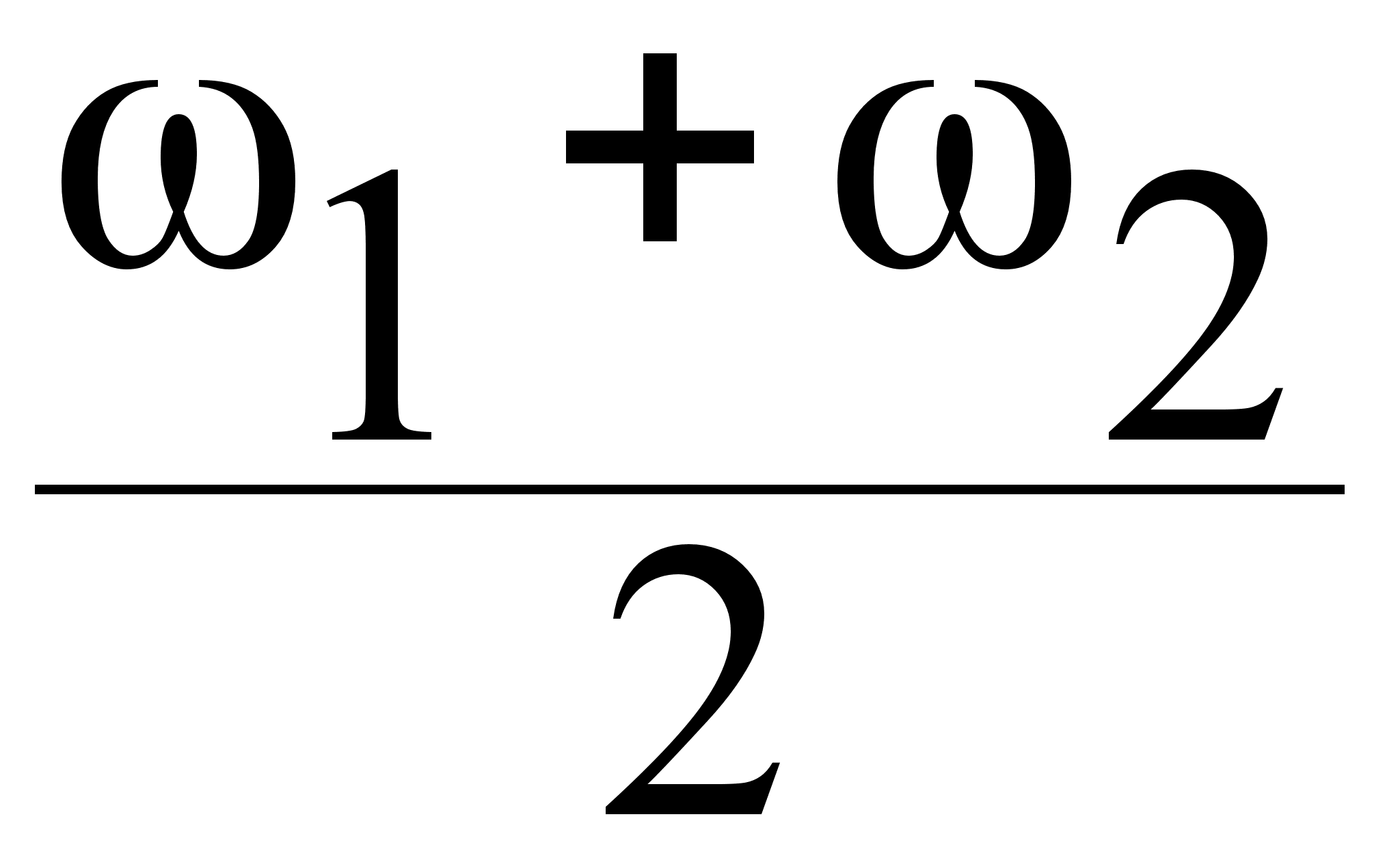 = 0
= 0
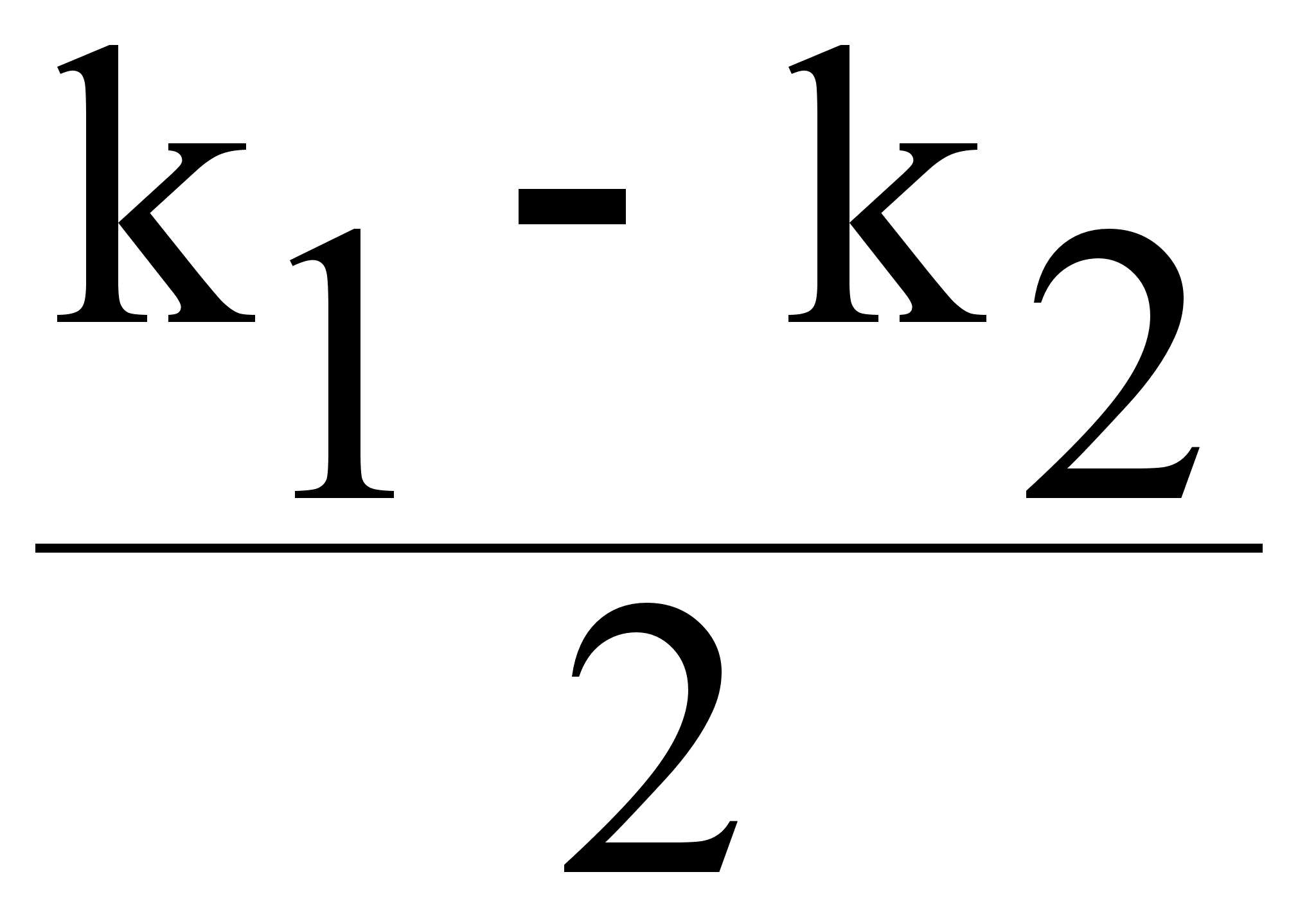 = k
= k 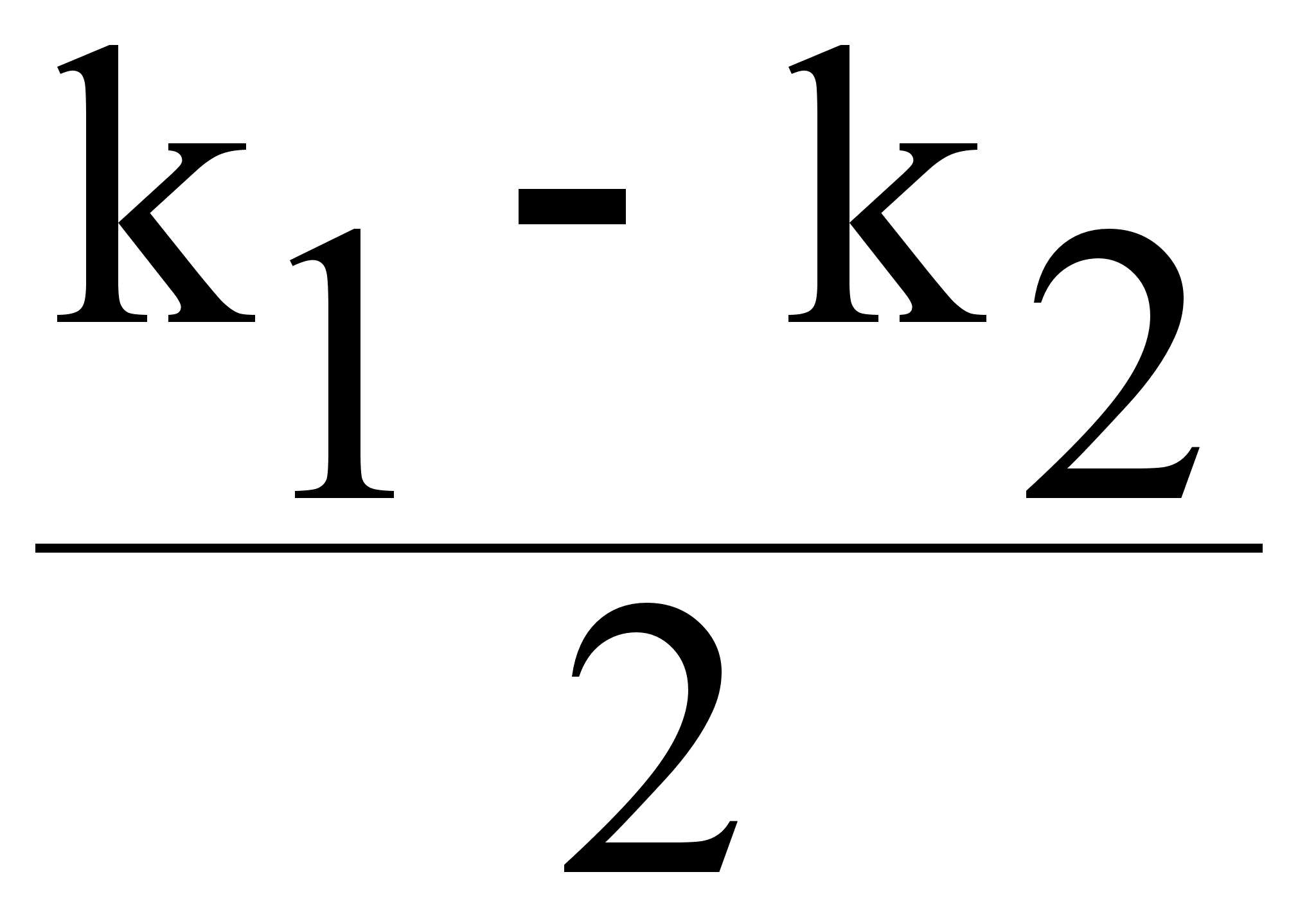 = k0
= k0
<< 0 k << k0
= 2 A cos (t - k Z) cos (0t - k0Z) (7.4.2.)
----------------------- -------------------
описывает медленно описывает быстро изменяющийся волновой процесс.
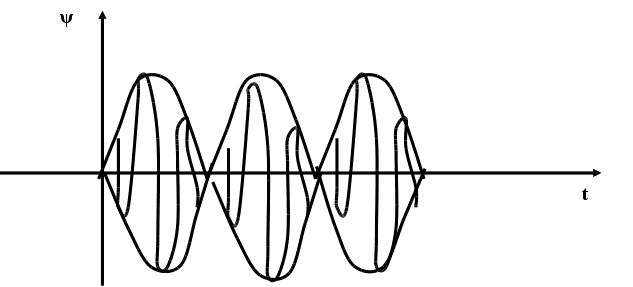
При оценке скорости реальных сигналов, специалисты рассматривают скорость переноса max энергии. Рассмотрим с какой скоростью изменяется в пространстве фронт max амплитуд.
в т. Z1 , t1 Ф1 = t1 - kZ1 ,
в т. Z2 , t2 Ф2 = t2 - k Z2
Ф1 = Ф2t1 - kz1 = t2 - k Z2
k (Z2 - Z1) = (t2 - t1)
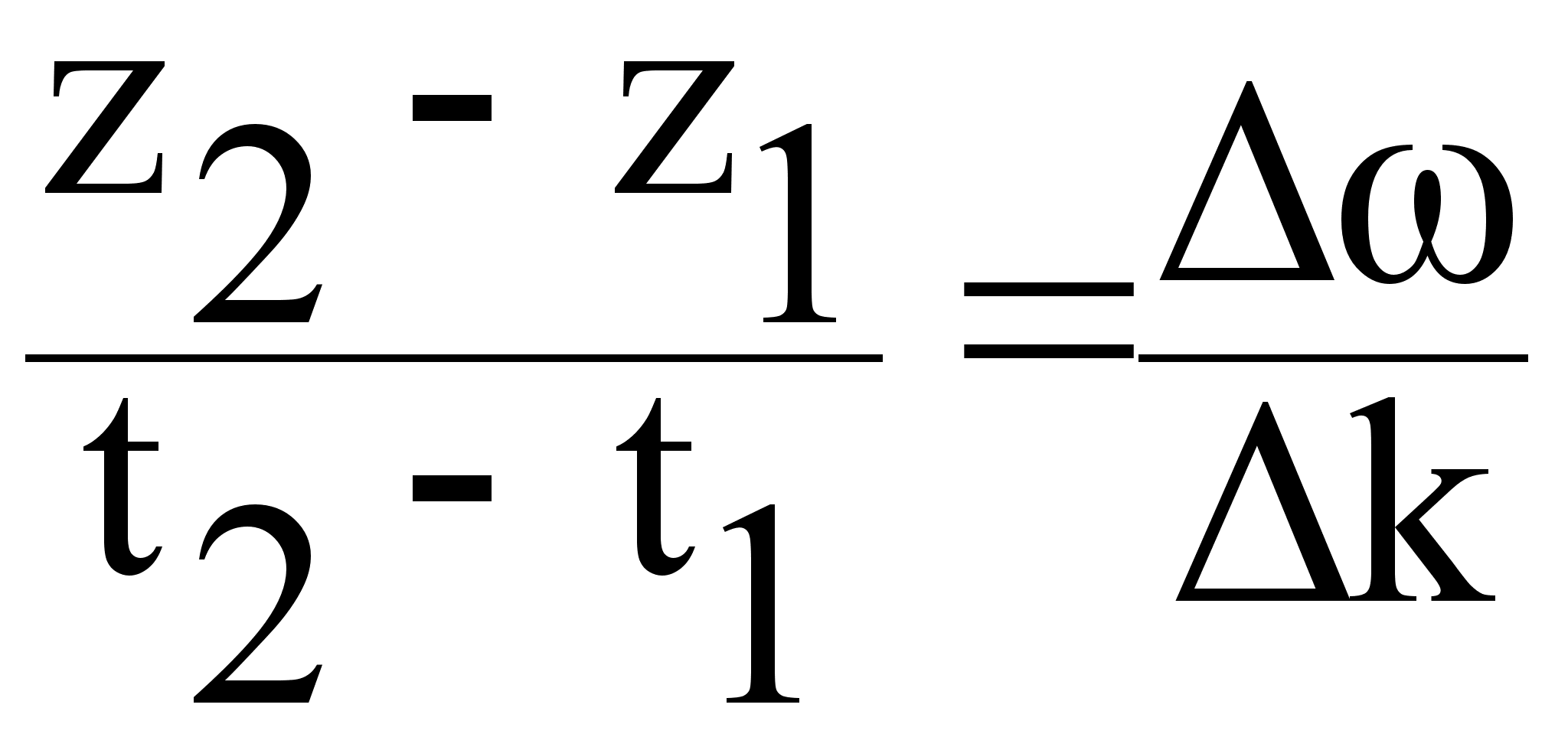 =Vгр
=Vгр


![]() = Vгр
= Vгр![]() (7.4.3.)
(7.4.3.)
Vгр по физическому смыслу характеризует скорость перемещения огибающей сигнала. С движением огибающей связано перемещение энергии, поэтому с групповой скоростью связано перемещение энергии:
Vгр c Vф >< c
Vф связана с изменением состояния, а не с переносом энергии.
Vф - скорость изменения состояния фазового фронта.
П ример: Лампочки последовательно загораются, изменение скорости состояния загорания может сколько угодно большой.
ример: Лампочки последовательно загораются, изменение скорости состояния загорания может сколько угодно большой.
7.5. Поляризация плоских электромагнитных волн
Под поляризацией будем понимать заданную в
пространстве ориентацию вектора Е или Н. Различают 3 вида поляризации: линейную (вектор Е и Н ориентирован всегда вдоль одной линии прямой),
круговую поляризация (вектор Е или Н вращается по кругу), эллиптическую поляризация (вектор Е или Н вращается по эллипсу).
Возьмем два ортогональных колебания:
Ех = А cos (t - kz)
Ey = B cos (t - kz + ) (7.5.1.)
- показывает сдвиг во времени, они не совпадают по фазе.
Что получится в результате сложения двух ортогональных колебаний ?
1) А В амплитуды разные, а сдвиг фаз равен 0.
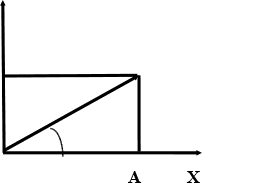 y ( = 0)
y ( = 0)
_____ ___________
в E = E2x + E2y = A2 + B2 cos (t-kz)
= arctg 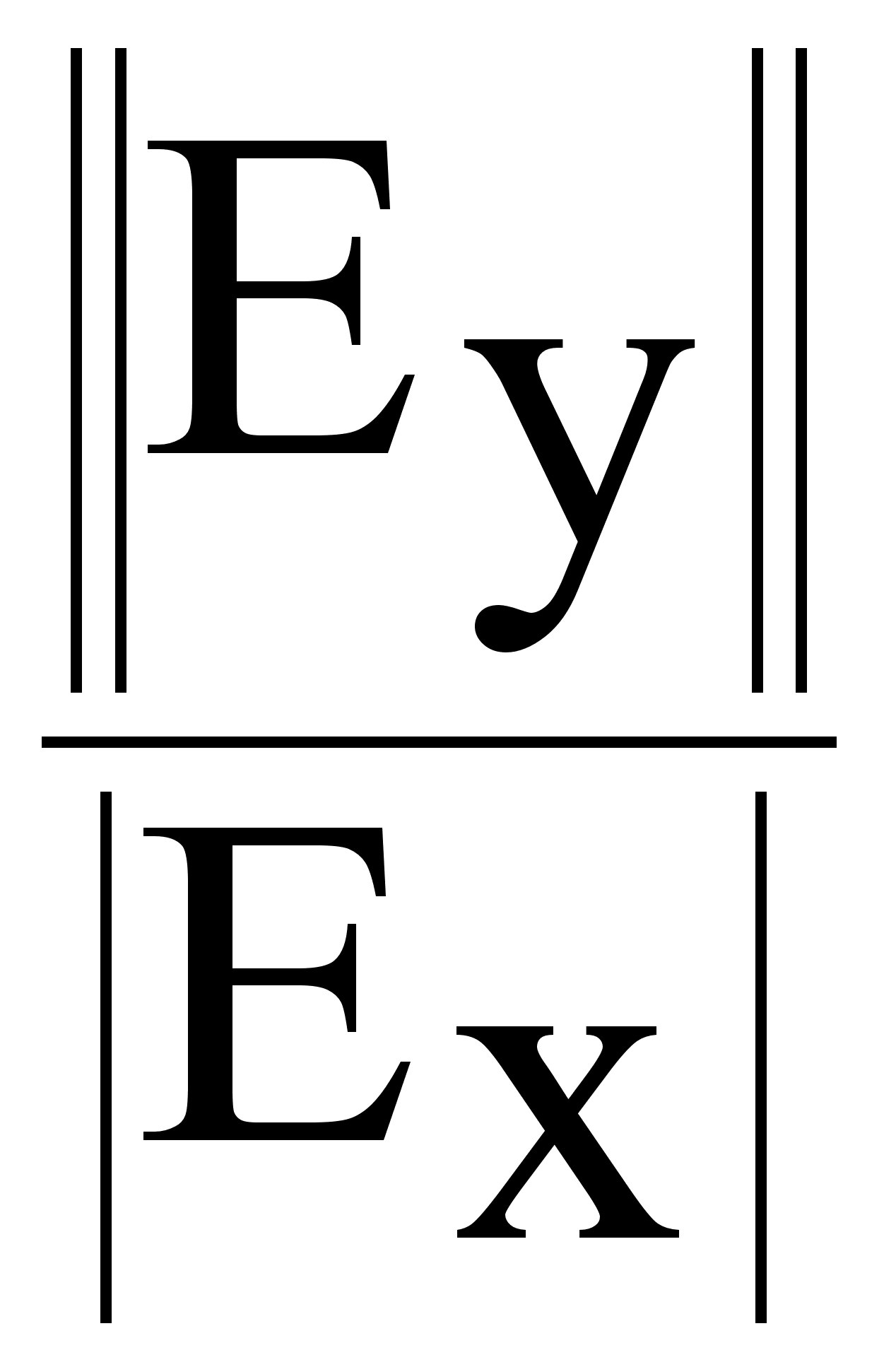 = arctg (
= arctg (![]() ) (7.5.2.)
) (7.5.2.)
Сложение двух ортогональных линейно- поляризованных колебаний, изменяющихся в одной фазе, но с разной амплитудой дает линейно- поляризованное колебание ориентированное под некоторым углом.
2) А = В ; = (/2)
Два ортогональных колебания по определению:
= arctg (![]() ) = arctg
) = arctg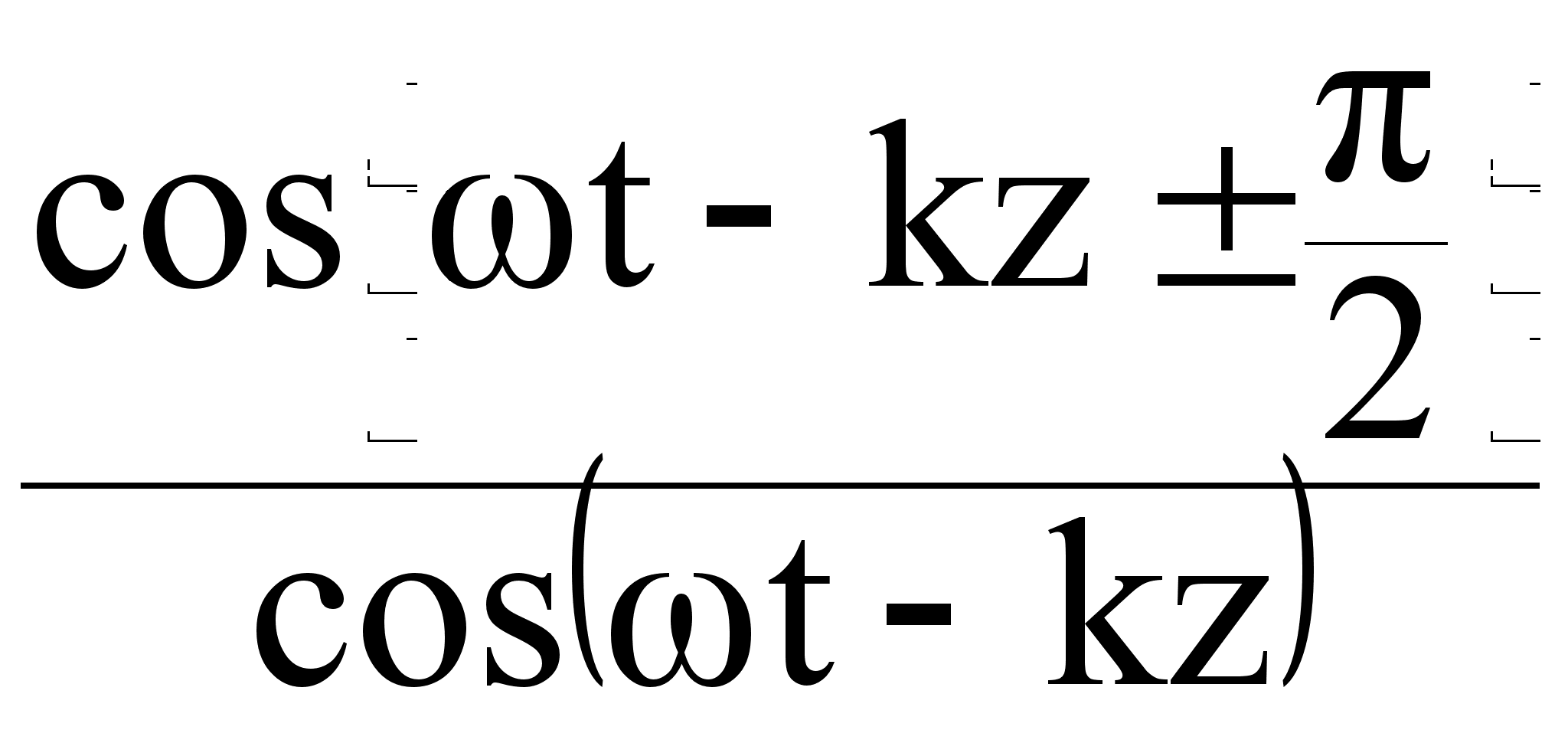 =
=
= arctg tg (t - kz) = (t - kz)
Сложение двух ортогональных линейно- поляризованных колебаний изменяющихся с одинаковой амплитудой и фазой со сдвигом /2 дает вращающее колебание (колебание с круговой поляризацией).
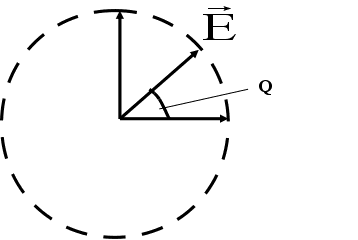
___________ _____________________________
E =E2x+E2y=A2cos2 (t - kz) + A2sin2 (t - kz) = A
E = A
Направление вращения определяется опережением или отставанием по фазе.
3) В общем случае, когда А В, и фазы разные, вектор
Е или Н вращается по эллипсу.
Любую волну с линейной поляризацией можно представить в виде двух волн с круговой поляризацией, имеющих разное направление.

1 2 3 4 5
Явление поляризации широко используется на практике. Все приемные устройства (служебная связь - вертикальная поляризация, в России прием ТВ на горизонтальную поляризацию, вертикальная поляризация - режим передачи, горизонтальная - режим приема. Круговая поляризация широко используется в радиолокации.
Подобные работы: