Поверхневі напівпровідникові хвилі в напівпровідникових структурах
Міністерство освіти України
Національний педагогічний університет
ім. М.П.Драгоманова
Курсова робота з загальної фізики на тему:
“Поверхневі електромагнітні хвилі в напівпровідникових кристалах.”
Київ - 1998
План.
Вступ.
Теорія оптичних констант.
Що таке “Поверхневий поляритон”.
Основи методу ППВВ.
Дослідження структури ZnO на сафірі методами ІЧ спектроскопії.
Поверхневі поляритони в стуктурі ZnO на сафірі.
Висновки.
Застосування матеріалів роботи в середній школі.
Список використаної літетатури.
Вступ.
Одним з перспективних напрямків сучасної фізики є дослідження поверхні твердого тіла та взаємодії поверхневих електромагнітних хвиль інфрачервоного діапазону з поверхнею та тонкими шарами напівпровідників . Поверхня впливає на ефективність роботи напівпровідникових приладів. З різними аспектами фізики поверхні пов`язані проблеми створення плівочних елементів, нанесення зміцнюючого покриття, міцності, коррозії, адсорбції та ін.
При взаємодії світлової хвилі з поверхнею твердого тіла виникає поверхнева електромагнітна хвиля. Слід зауважити , що під поверхневою електромагнітною хвилею розуміють хвилю, максимум якої знаходиться на поверхні твердого тіла і амплітуда поля якої зменшується по експоненціальному закону при віддаленні від межі розподілу середовищ. Квазічастинки, які відповідають цим коливанням, що мають змішаний електромагнітно-механічний характер, називають поверхневими поляритонами (ПП). Не зважаючи на екзотичну назву, ці хвилі можуть бути знайдені в рамках феноменологічної електродинаміки як роз`вязки рівнянь Максвелла для межі двох середовищ . Дисперсія таких поверхневих хвиль в кристалі визначається залежністю його діелектричної проникності від частоти падаючого світла. Під фононом розуміють квазічастинку , що відповідає механічним коливанням решітки, тобто періодичним зміщенням атомів відносно положення рівноваги. Плазмон- це теж квазічастинка, але вона описує коливання вільних електронів навколо важких іонів. При деяких умовах плазмони та фонони можуть взаємодіяти.
Фотони при зіткненні з ідеально гладкою межею розділу не взаємодіють або “не бачать” поверхневі поляритони на цій межі. Якщо ж поблизу поверхні покладено призму, або сама поверхня шорохувата, чи на неї нанесена дифракційна решітка, то поверхневі поляритони можуть збуджуватись падаючим фотоном. Ці явища покладено в основу дослідження поверхневих хвиль. Такими методами є :
метод модифікованого багатократного порушеного внутрішнього відбивання ;
метод модифікованого повного внутрішнього відбиття;
метод комбінаційного розсіяння світла.
Зараз розроблено ефективні методи дослідження структури поверхні. В них використовується розповсюдження в кристалах світлових хвиль з певними значеннями частоти та хвильового вектора. Порівняння залежності
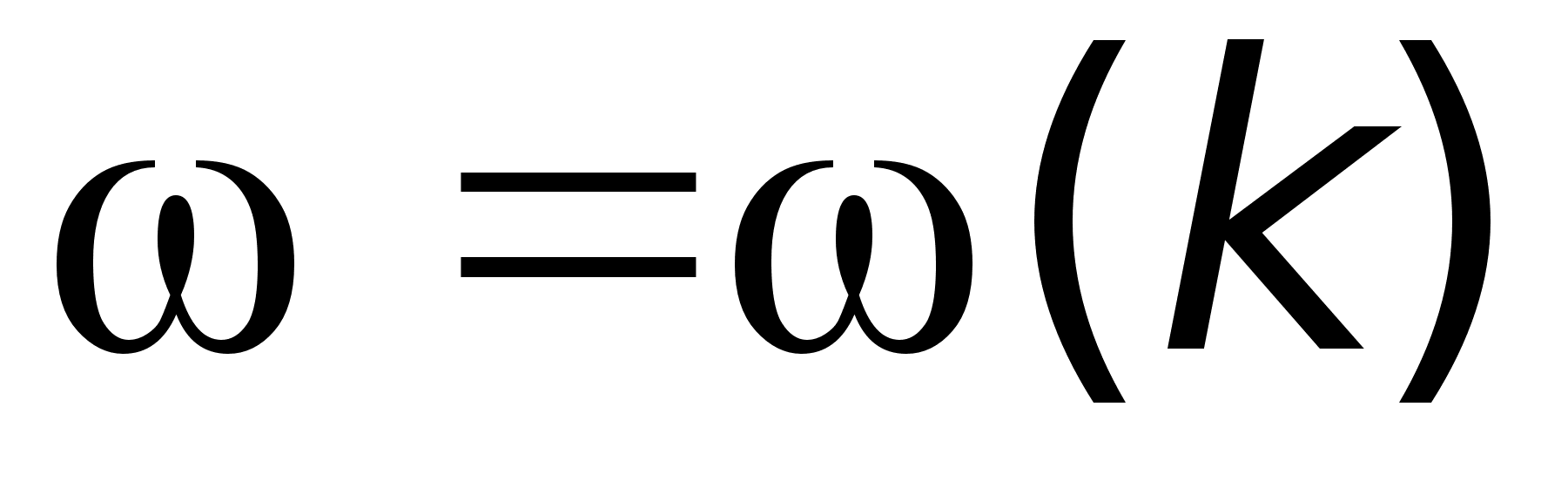, отриманої з рівнянь Максвела, з експериментально отриманою дисперсією хвиль, що розповсюджуються в кристалах , дає можливість отримувати інформацію про спектр поверхневих збуджень середовища.Вибір карбіда кремнію в ролі одного з матеріалів для експериментальних досліджень обумовлений перспективою його використання в напівпровідниковій мікроелектроніці. Дійсно, прилади на основі карбіду кремнію, завдяки його унікальним фізико-хімічним властивостям, можуть використовувати в таких галузях науки і техніки, де потрібна підвищена надійність, радіаційна стійкість, робота при високих температурах.
Електрофізичні властивості карбіду кремнію відчутно залежать від конкретного політипу. Зараз відомо понад 200 модифікацій карбіду кремнію.
Позначення політипів в символах Рамсделла складається із цифри, що позначає число шарів вздовж осі С, та букви Н або R в залежності від типу кристалу - гексагонального чи ромбоедричного.
Найбільш часто зустрічаються політипи SiC 6H, SiC 15R та
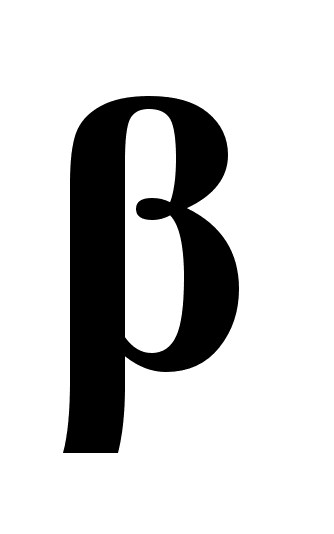SiC. Вони являються хорошими модельними кристалами для дослідження ПП, а також впливу різних поверхневих обробок на властивості ПП. Окрім цього, ідеальні кристали карбіду кремнію та епітаксіальні шари SiC на діелектричних підкладинках є перспективними для використання їх в мікроелектроніці та в інтегральній оптиці.1.Теорія оптичних констант.
Розповсюдження пучка променів в напівпровідниковому кристалі може бути описане розв`язком рівнянь Максвелла :
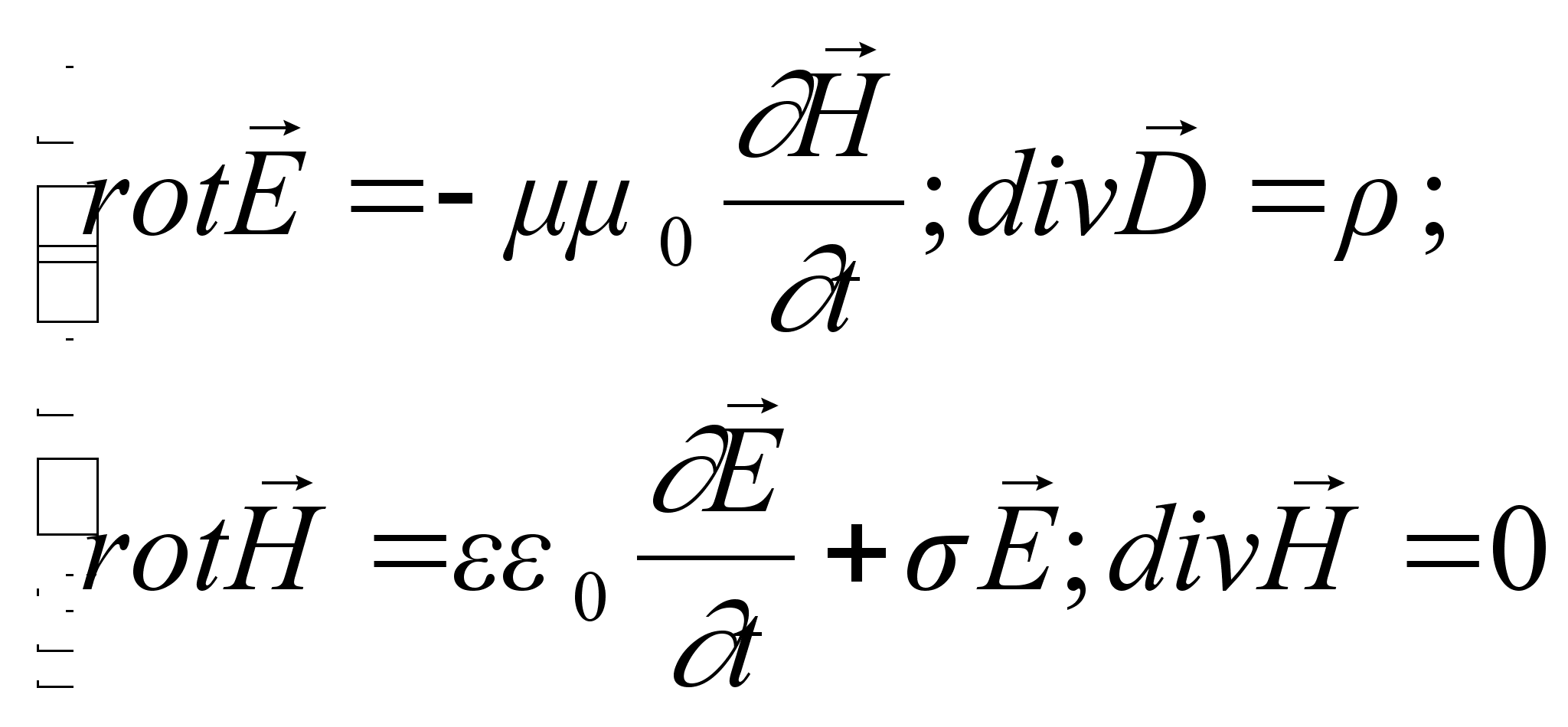, (1.1)В другому рівнянні системи , на відміну від діелектриків, врахована густина струму провідності
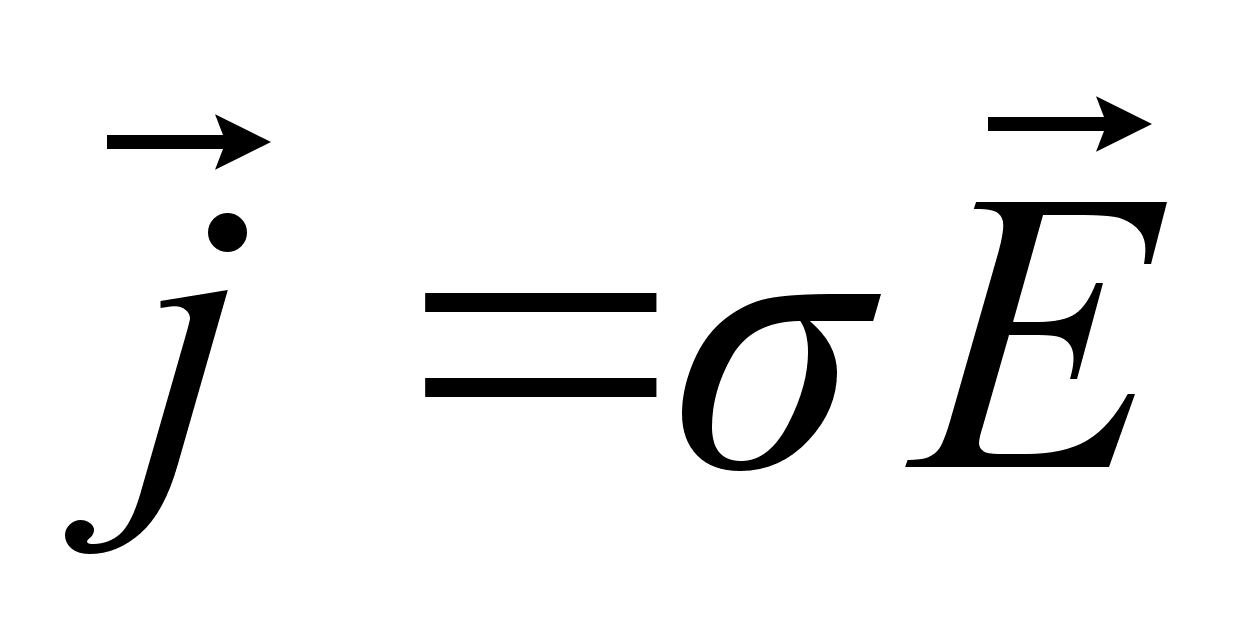, оскільки більшість напівпровідників по електричним властивостям ближчі до металів, ніж до діелектриків.В загальному випадку питома електропровідність
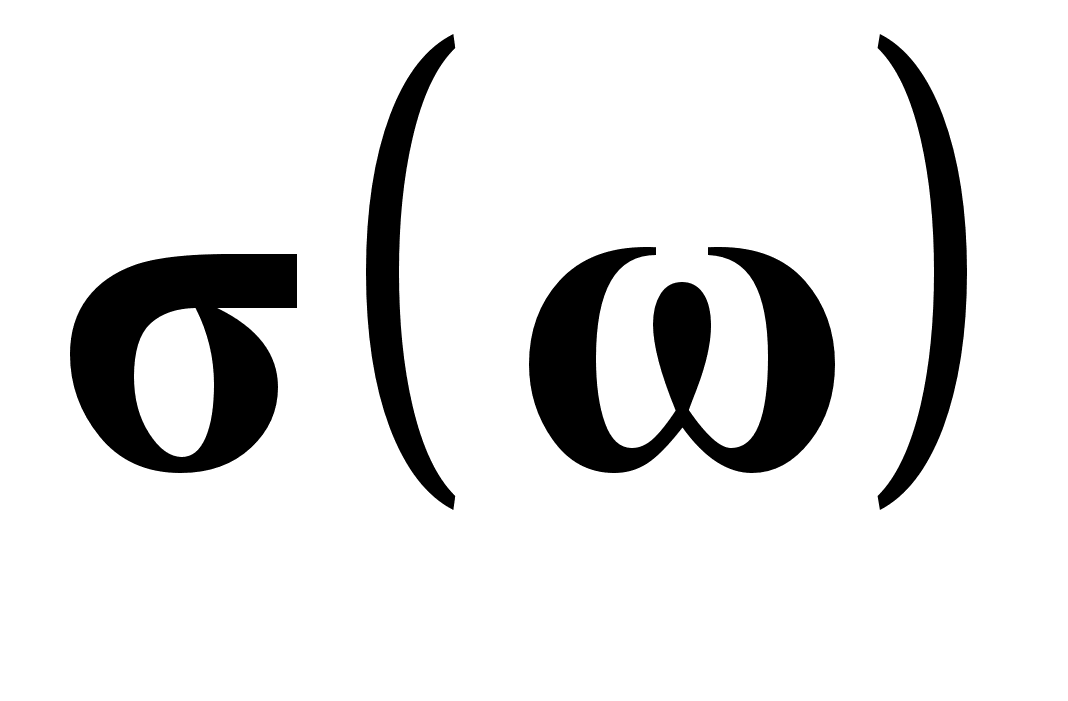, діелектрична 
та магнітна 
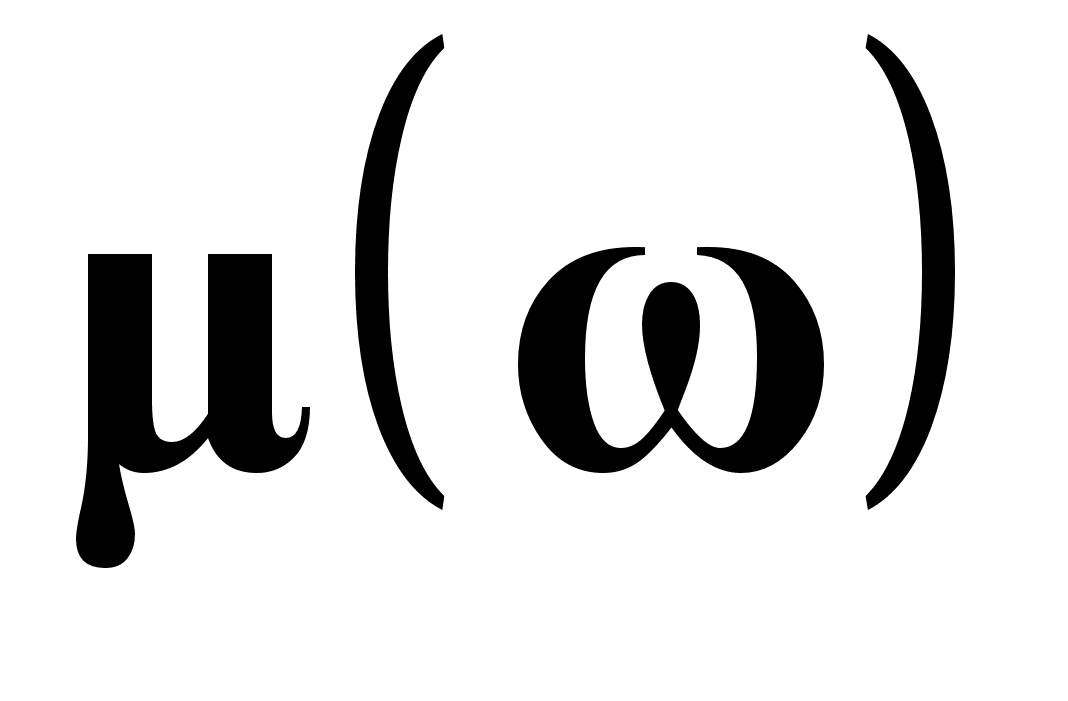проникності (відносні величини, що є функціями частоти) напівпровідника є анізотропними та представляються тензорами другого (або вище) рангів.Оскільки
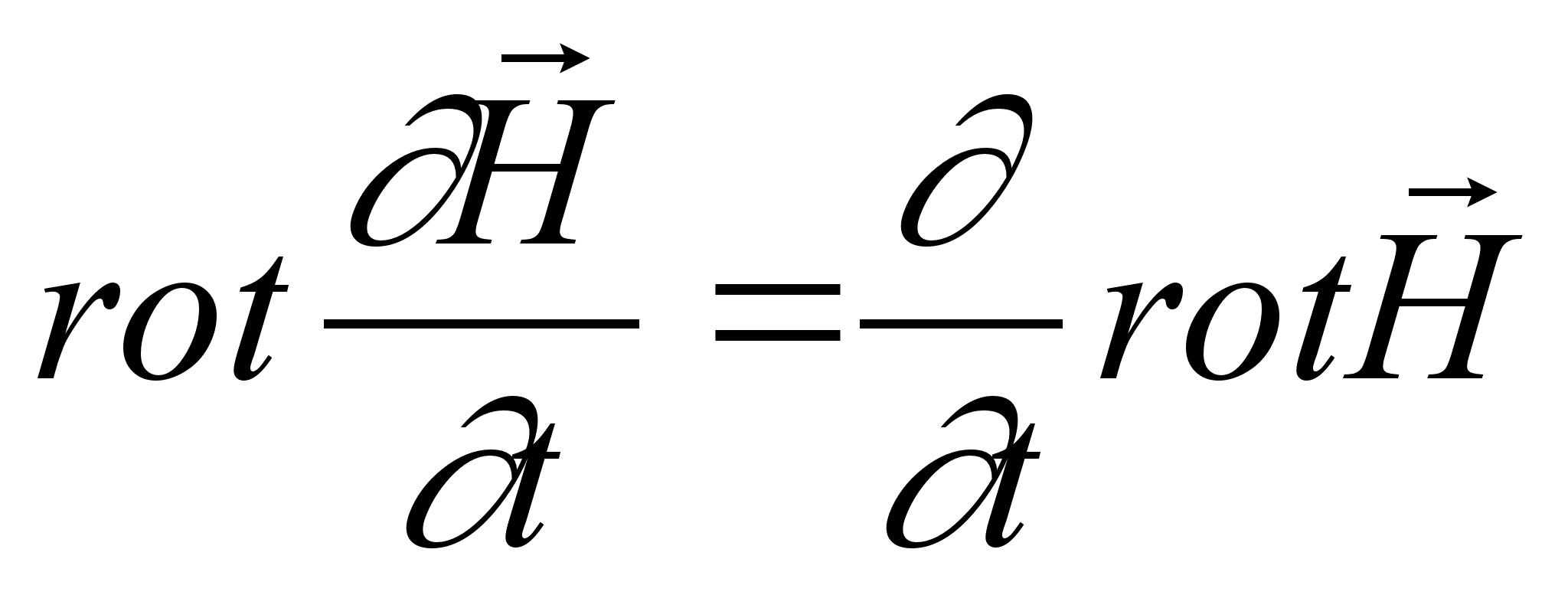,то:
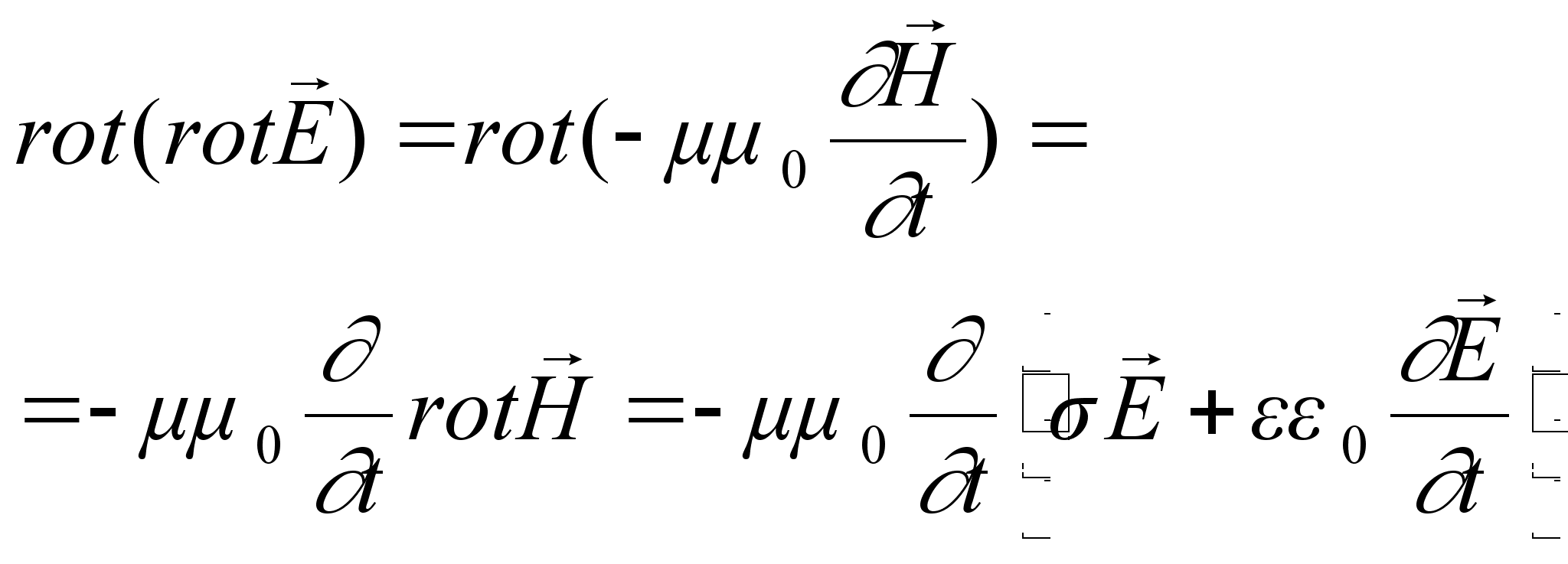
Але
а grad(div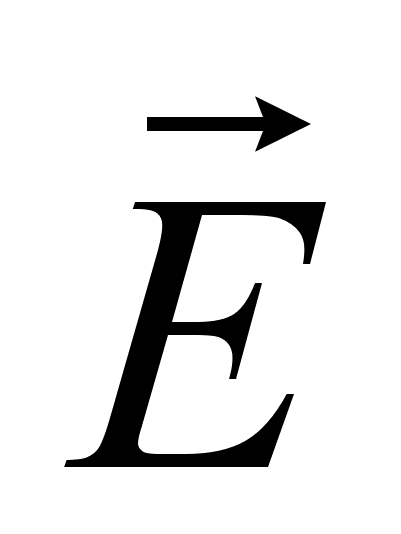
), тому
(1.2)Аналогічне рівняння можна отримати і для вектора напруженості магнітного поля
.Одним із можливих розв`язків рівняння (1.2) для вектора напруженості електричного поля є
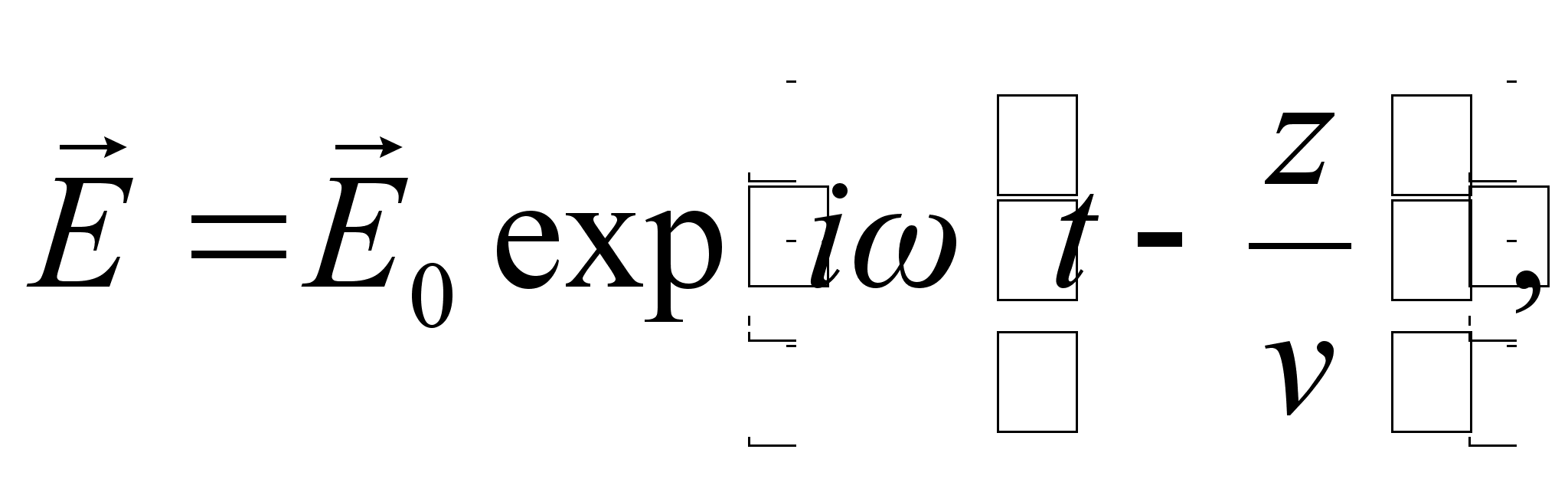(1.3)Це рівняння являє собою хвилю, що розповсюджується в напрямі z зі швидкістю v,
- кутова частота. Розв`язок (1.3) задовольняє (1.2) при умові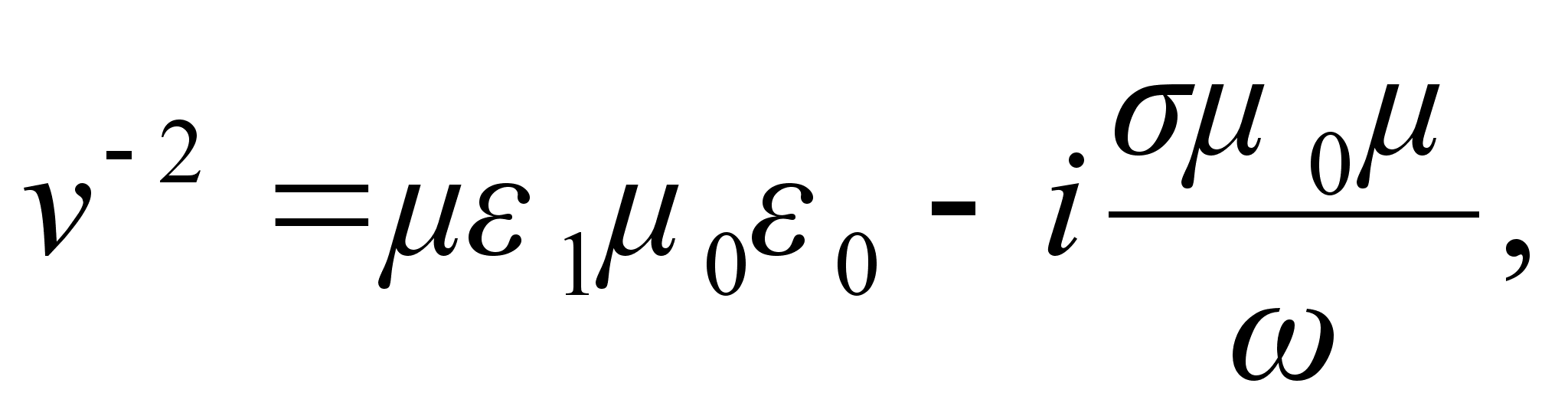
(1.4) а це задовольняє комплексному показнику заломлення
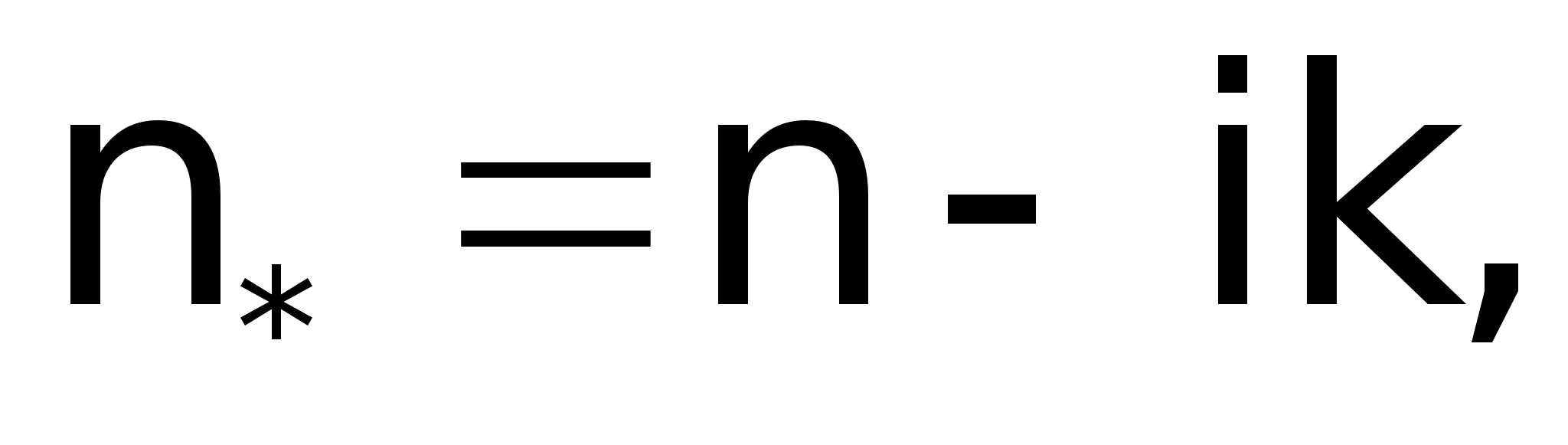(1.5)Враховуючи те, що квадрат швидкості поширення світла у вакуумі
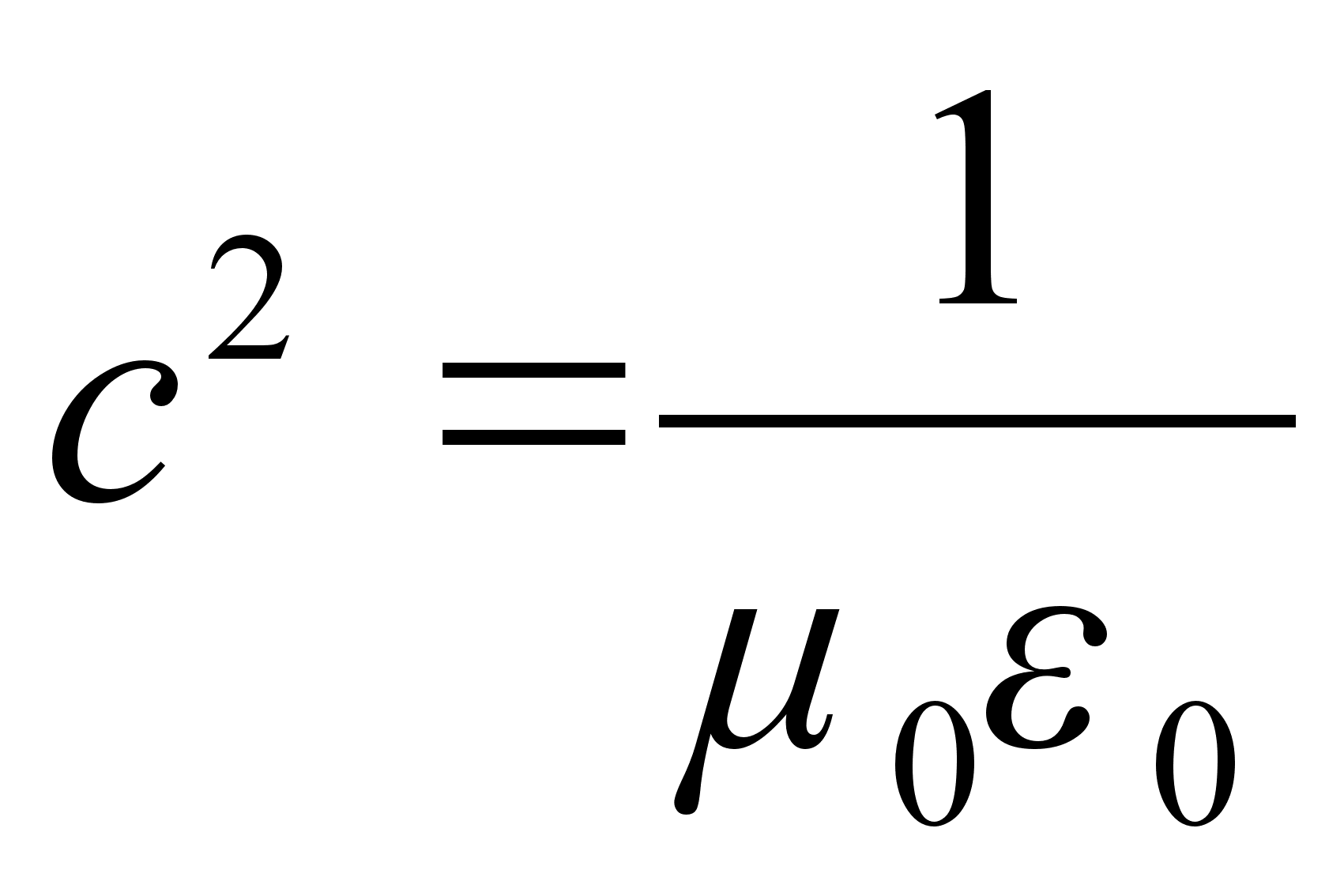, а також ту обставину, що в оптичному діапазоні більшість напівпровідників володіють слабкими магнітними властивостями, тобто 
співввідношення між головним показником заломлення n , головним показником поглинання k, з однієї сторони та діелектричної проникності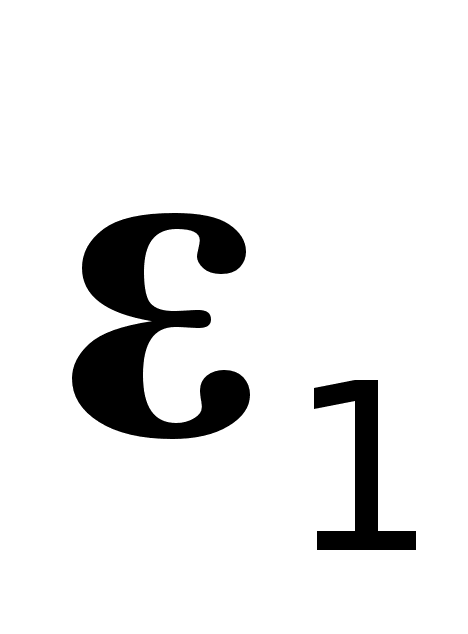 
, питомої електропровідності 
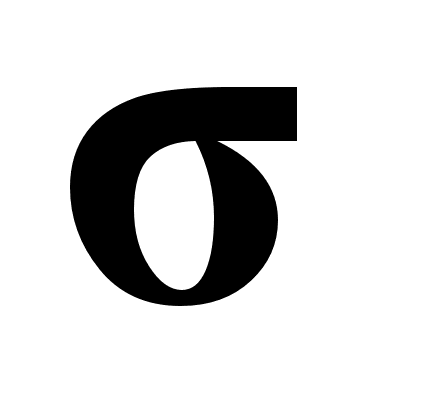- з іншої , приймає вигляд
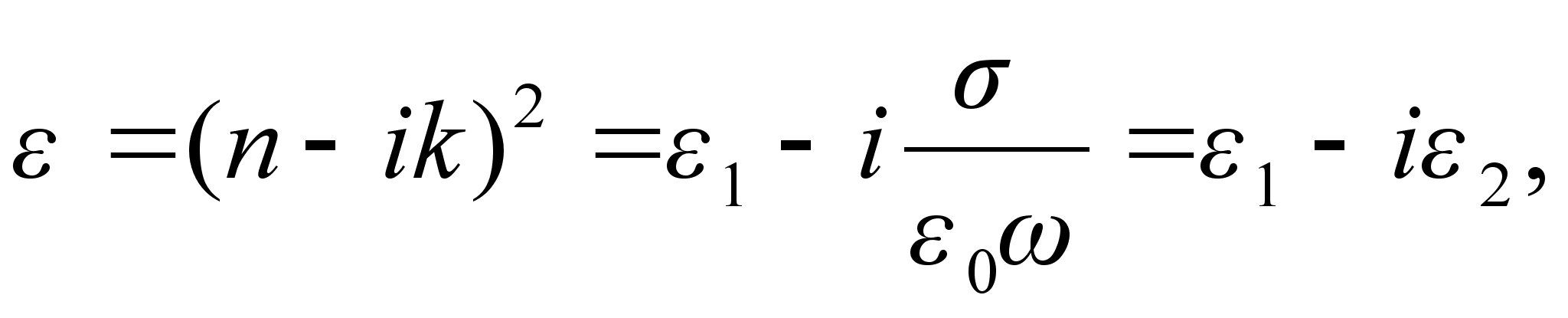(1.6)або після розділення дійсної та уявної частини
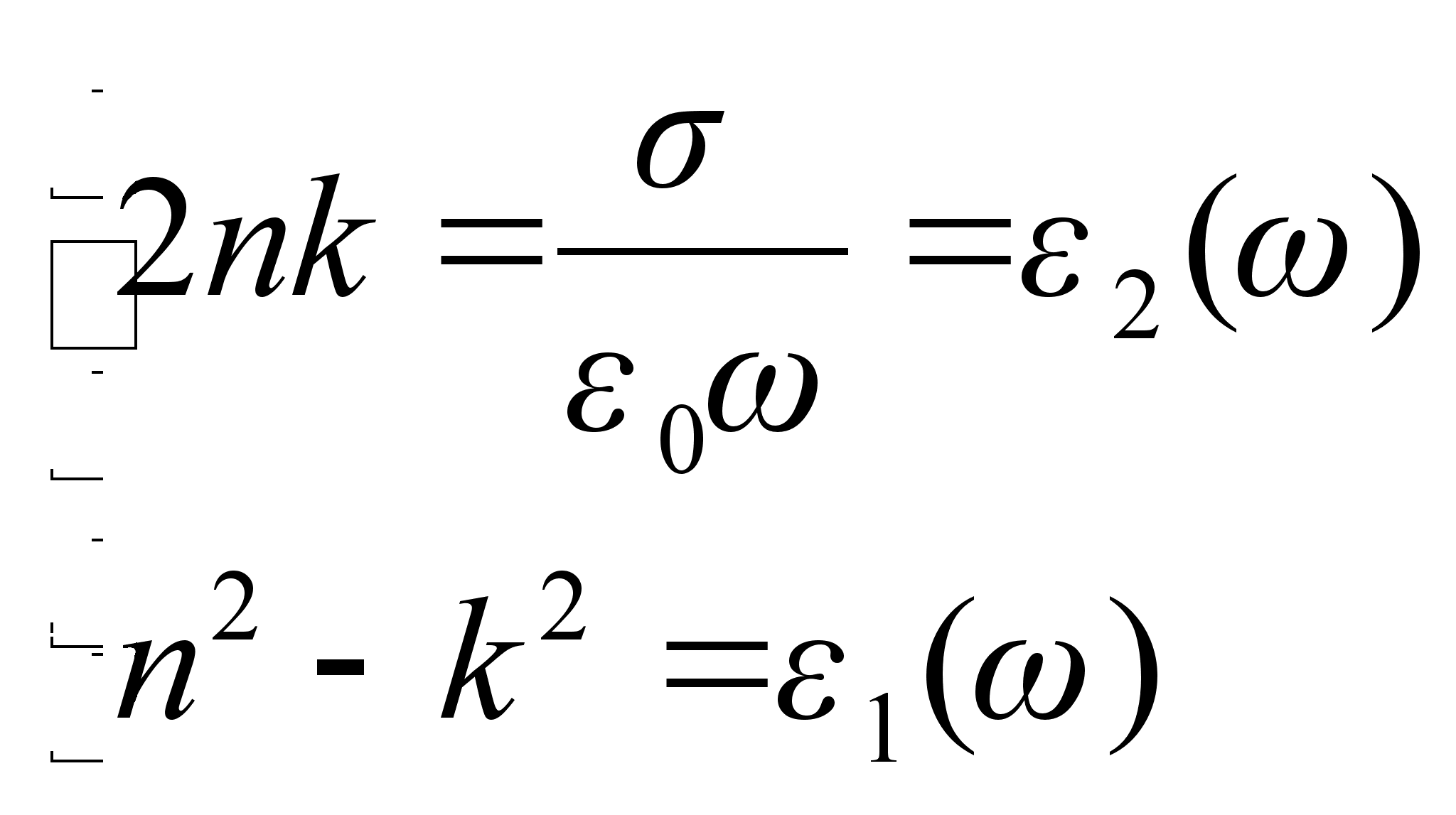, (1.7)Тут
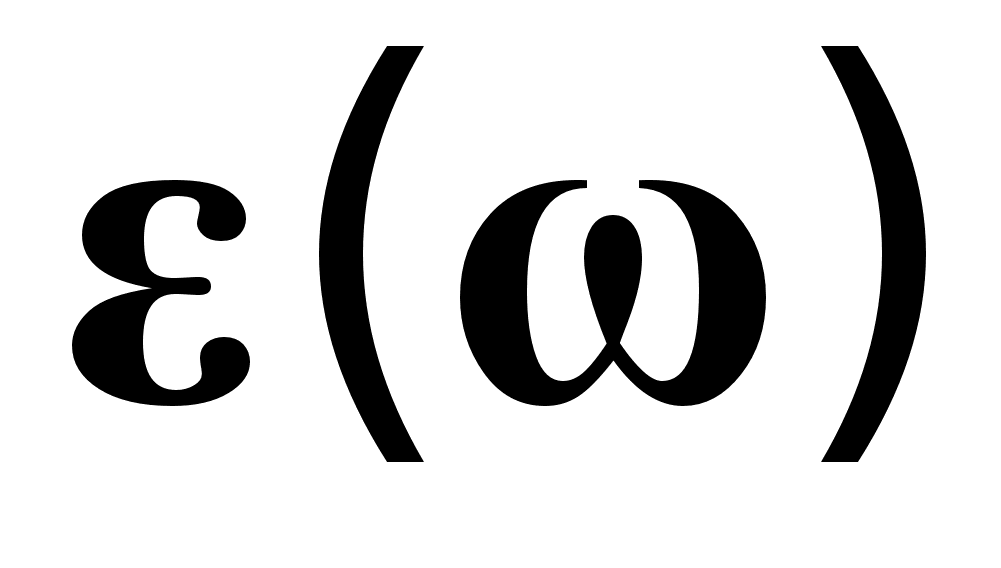- комплексна діелектрична проникність, в котрій по аналогії з n i k, 
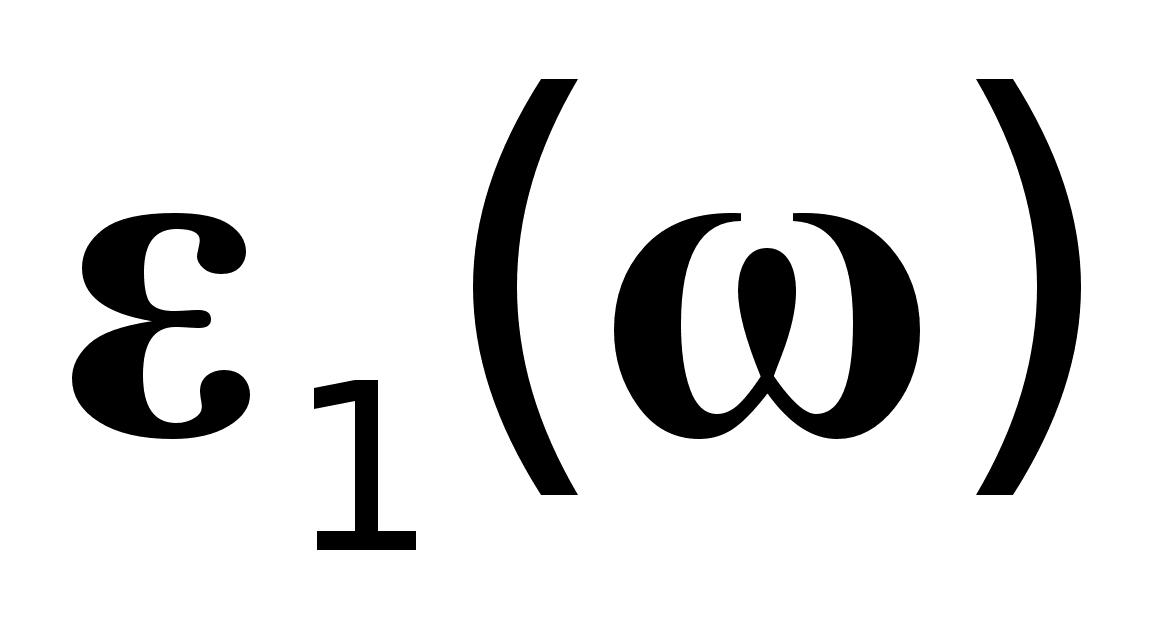- дійсна частина, а 
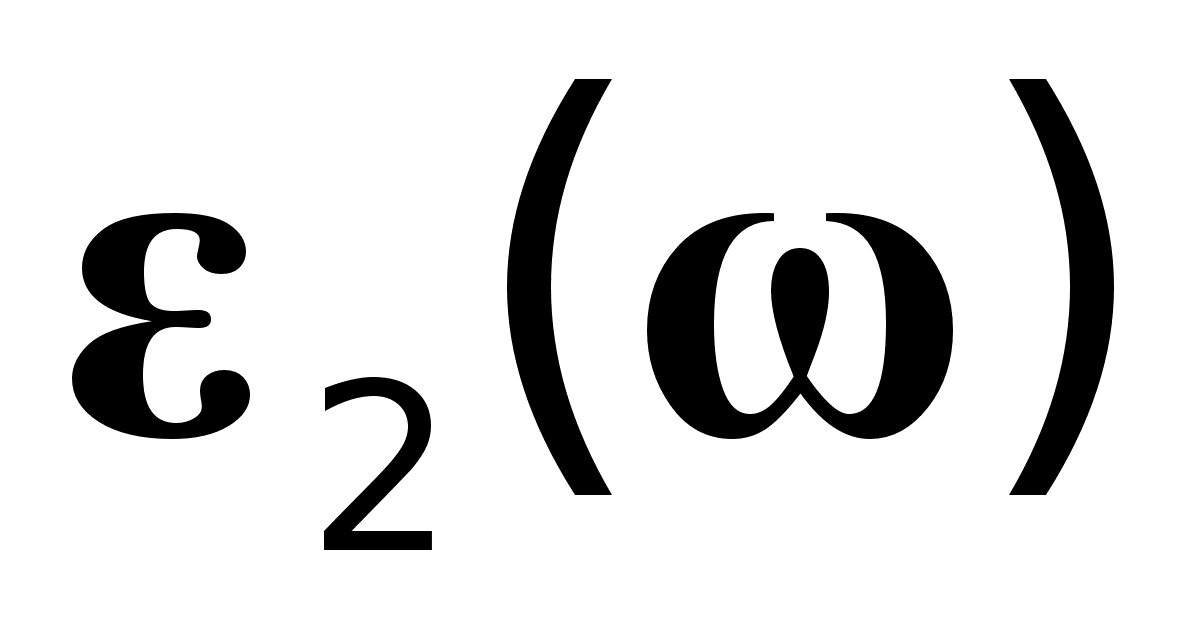- коефіцієнт при уявній частині. Спираючись на умову причинності можна записати формули, що пов`язують n i k одне з одним :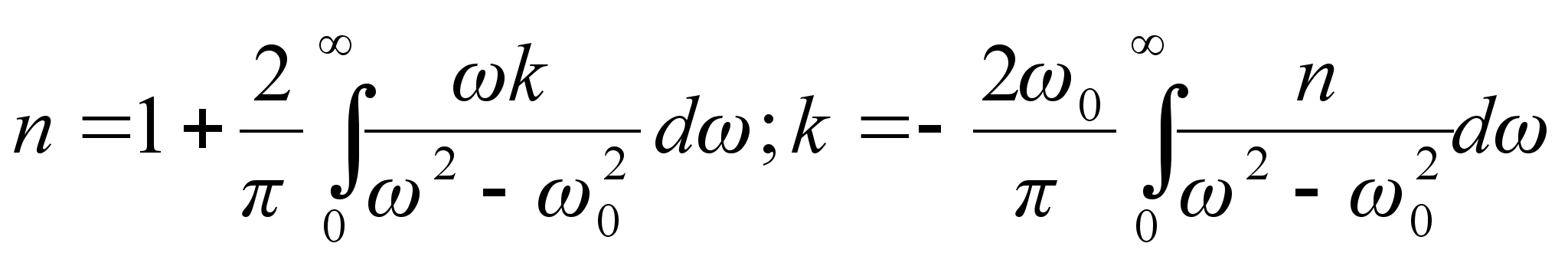
З першої формули n можна підрахувати для будь-якої частоти
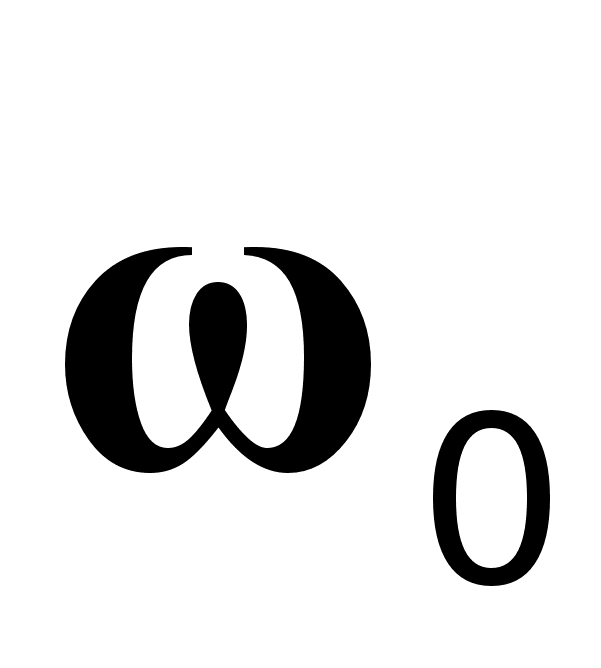в інтервалі від нуля до нескінченності, а значить на основі спектру поглинання може бути підрахований спектр показника заломлення і навпаки. Подібним чином можуть бути записані співвідношення, які пов`язують 
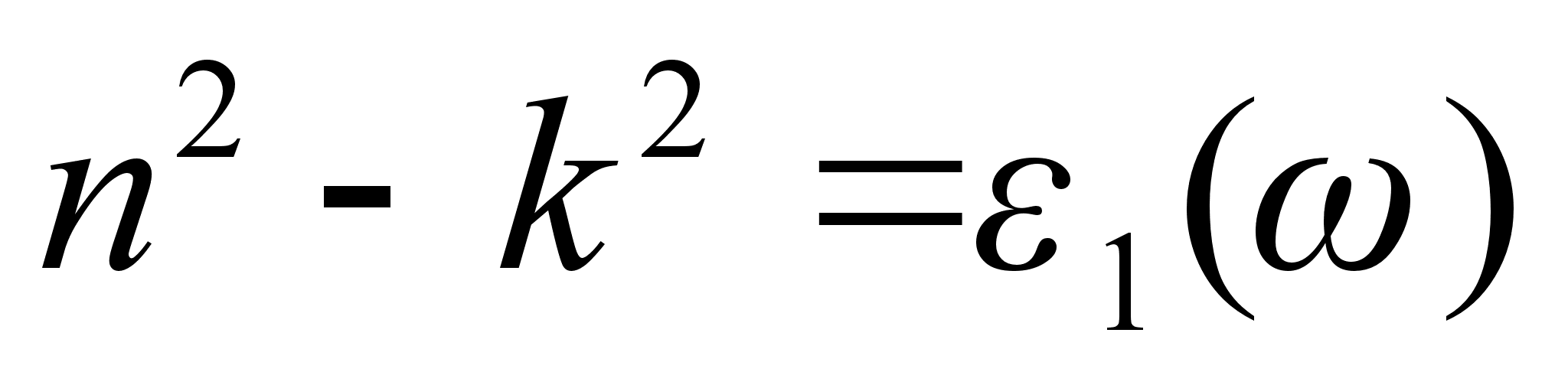та 
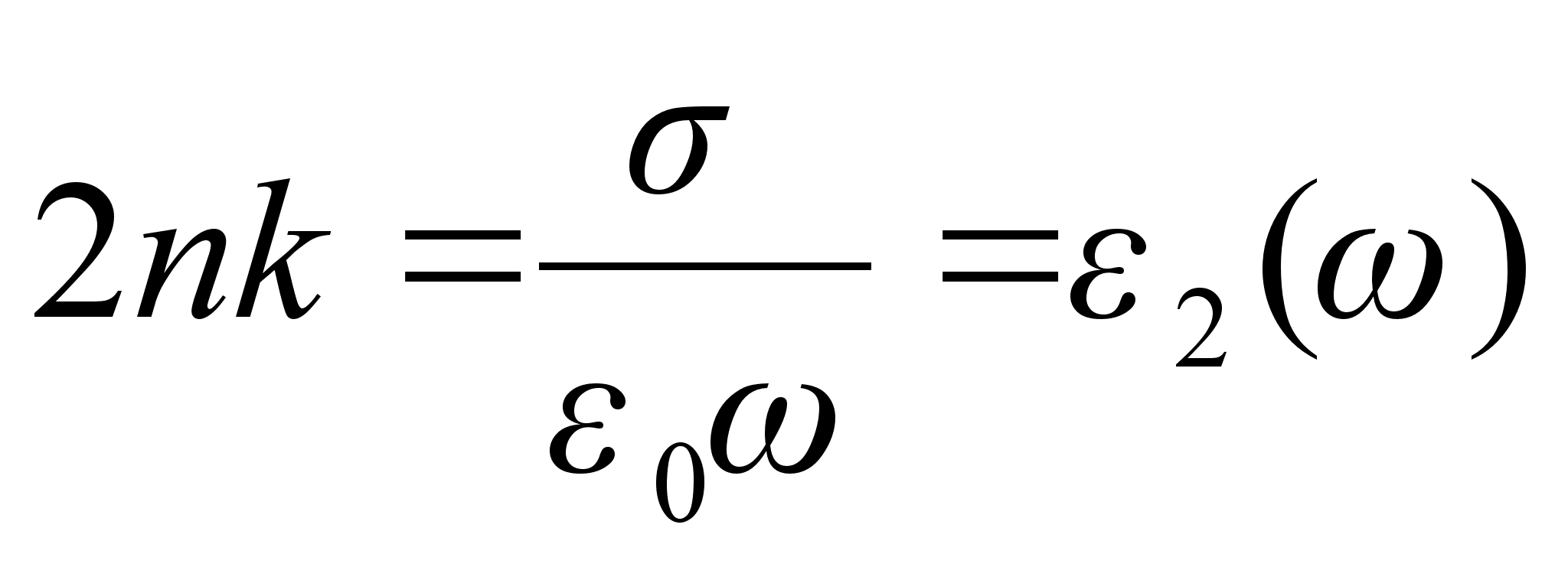
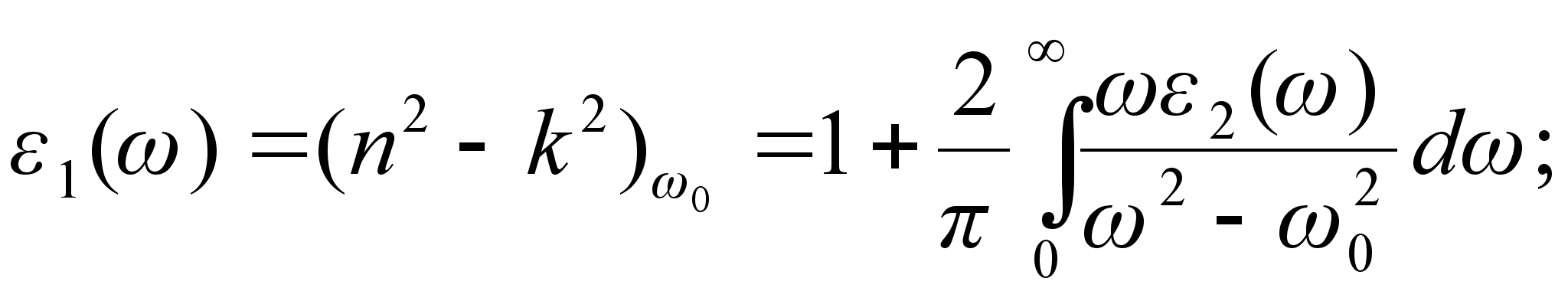(1.8)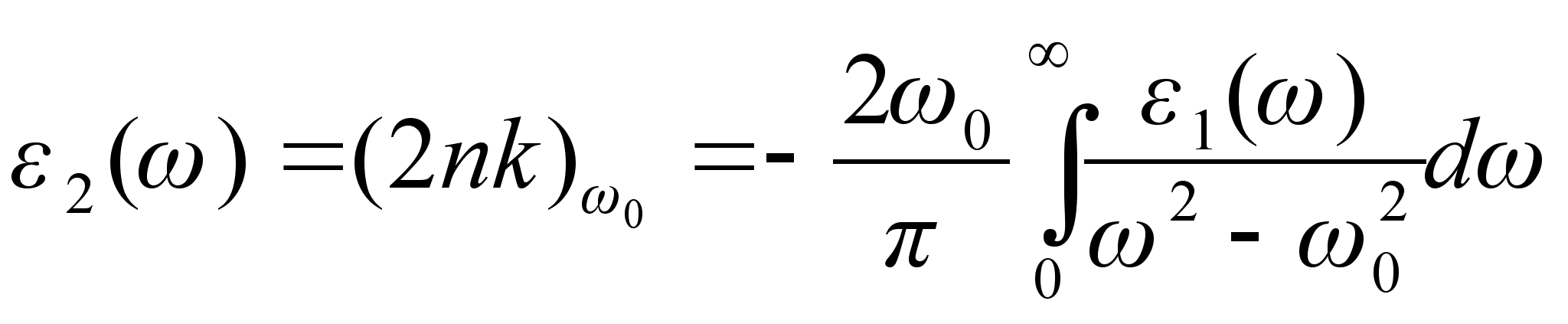
. (1.9)Це співвідношення Крамерса-Кроніга.
Тепер, підставивши (1.4) та (1.5) в (1.3), знайдемо
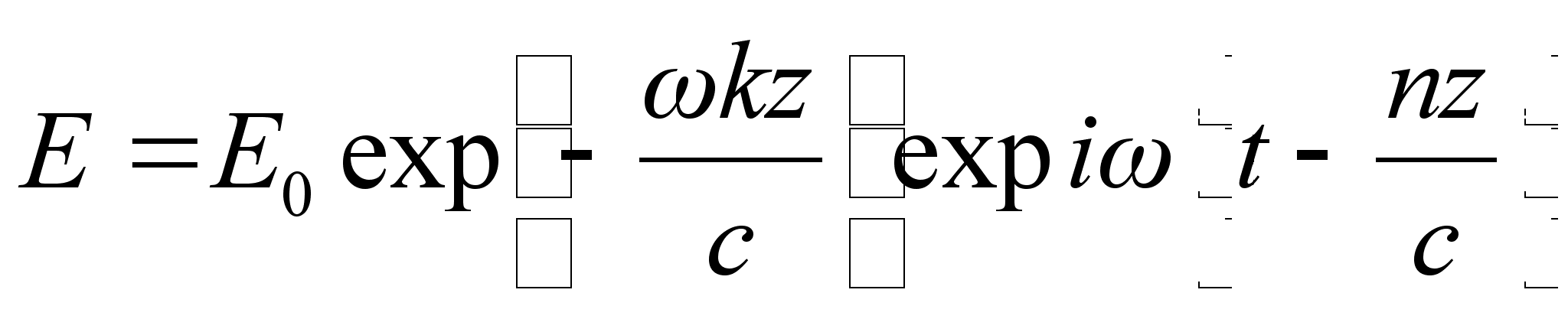, тут видно, що головний показник поглинання k характеризує затухання електромагнітної хвилі в напівпровіднику. Оскільки енергія хвилі пропорційна квадрату амплітуди , то для характеристики поглинання речовини часто застосовують замість 
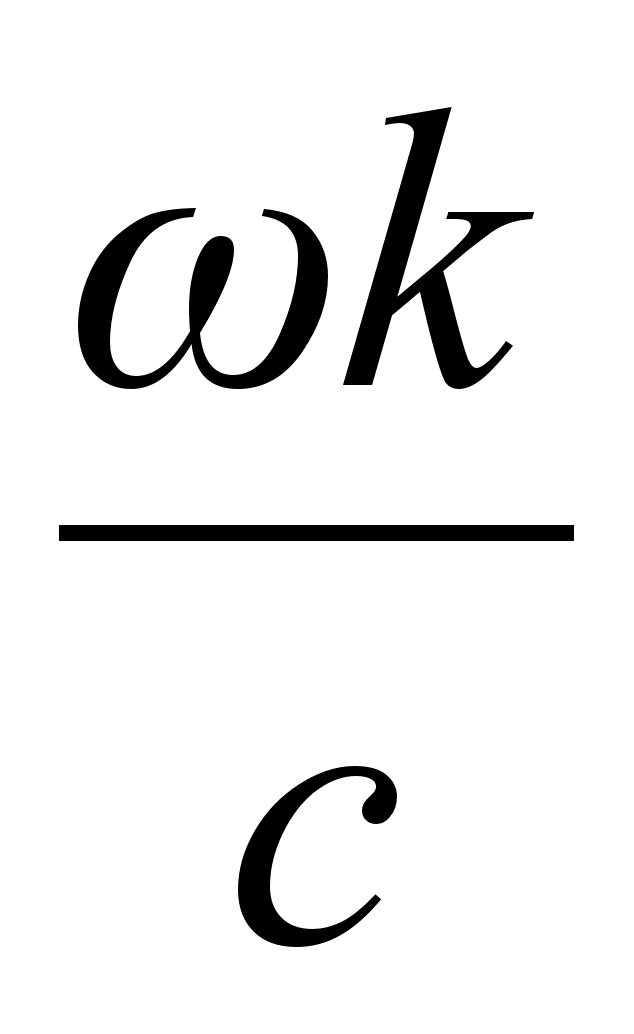величину
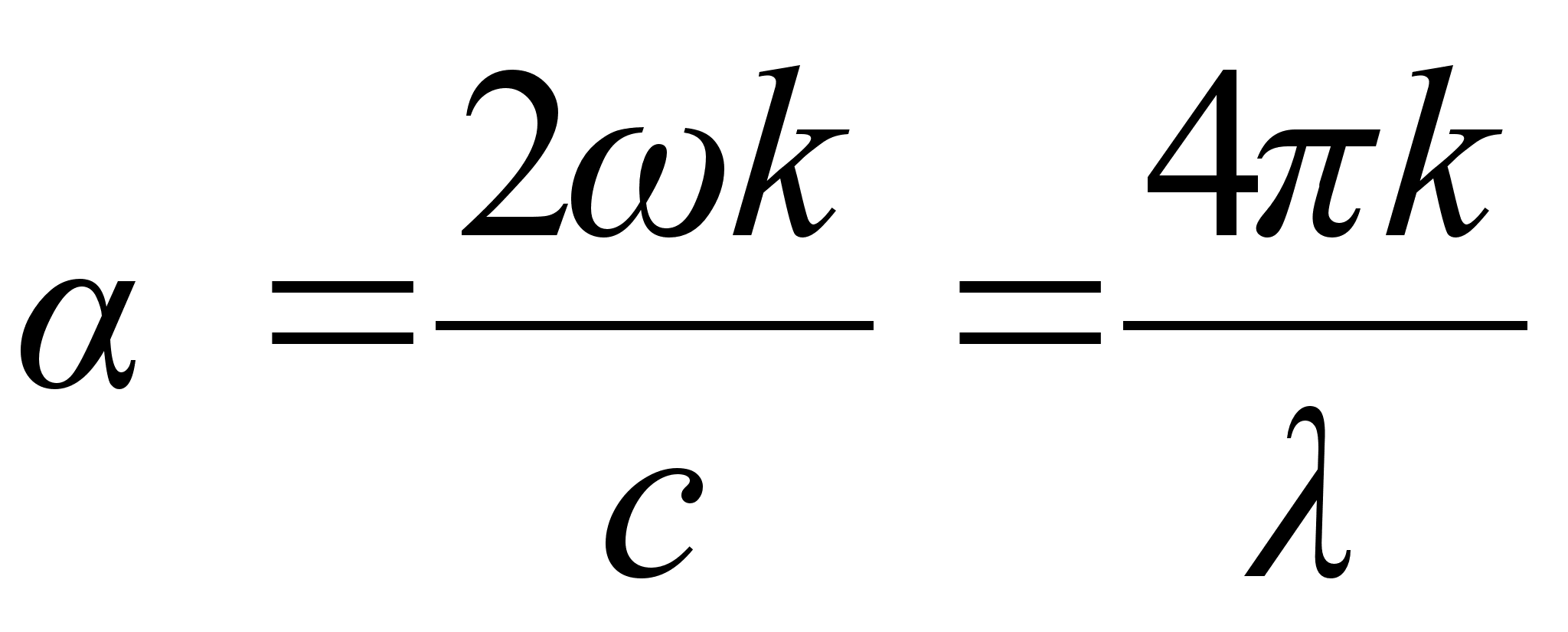, (1.10)це коефіцієнт поглинання , чисельно рівний оберненій товщині шару напівпровідника, в якому інтенсивність електромагнітної хвилі зменшується в e раз. Крім головного показника поглинання
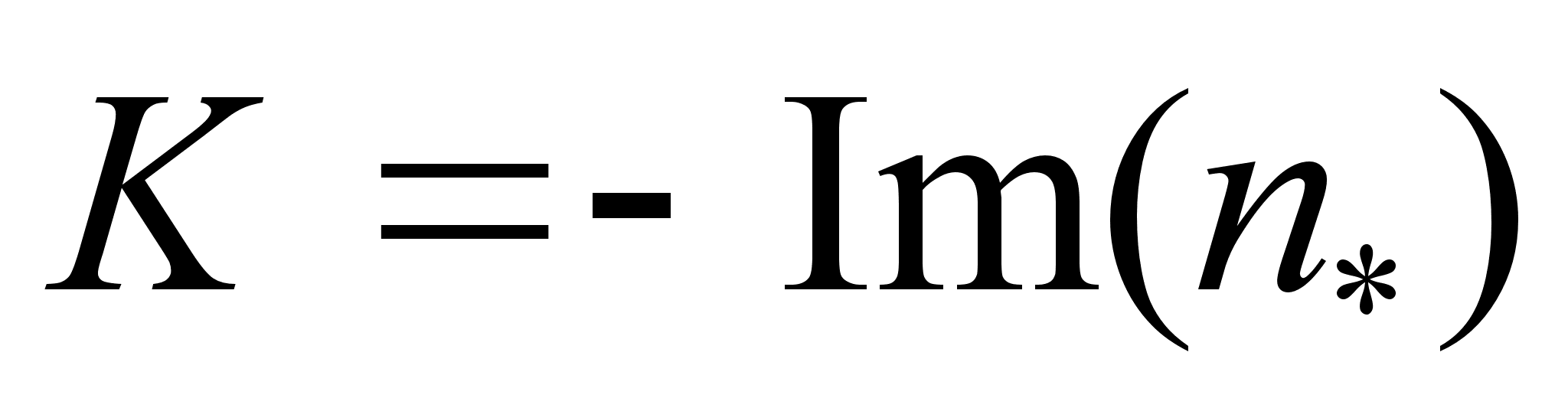, (1.11)рівного по величині , згідно формули (1.5) , уявній частині комплексного показника заломлення
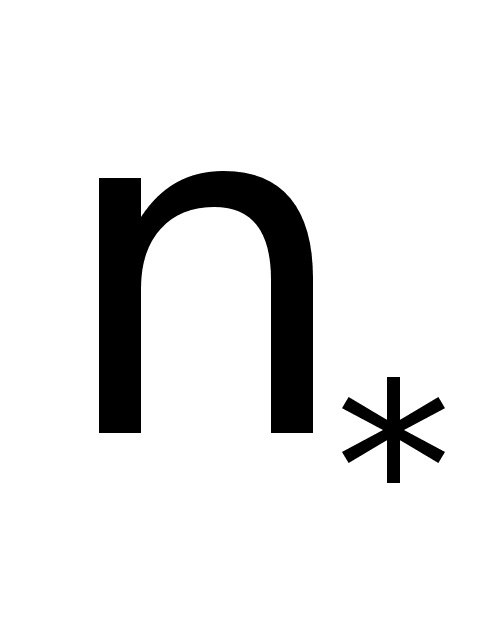, при деяких механізмах взаємодії електромагнітної хвилі і речовини можуть виникати особливі енергетичні витрати , котрі виражають формулою
, (1.12)2. Що таке “поверхневий поляритон”.
Термін “поляритон” був введений у 1957 р. Хапфілдом для позначення нормальної хвилі в кристалі. Пізніше Агранович використав його як скорочений еквівалент терміна “нормальна електромагнітна хвиля в середовищі”, тобто плоска монохроматична електромагнітна хвиля в нескінченному кристалі, що задовольняє макроскопічним рівнянням Максвелла.
На практиці термін “поляритон” найбільш часто використовують, коли частота електромагнітної хвилі попадає в окіл дипольно активного переходу в кристалі. В цьому випадку взаємодія електромагнітного поля з вказаним конкретним переходом є досить ярко вираженою і це призводить до “змішування” взаємодіючих підсистем - електромагнітної та “механічної” (коливання електронів або ядер).
Можна також говорити про поляритони у випадку не тільки кристалів, але й рідин і навіть газів, одначе характерні прояви ефектів змішування з індивідуальними дипольно активними переходами тут спостерігати складніше ( врідинах внаслідок великого затухання, в газах - відносно малої концентрації частинок речовини та ін.). Далі, говорячи про середовище, з яким зв`язано збудження поляритонів , будемо мати на увазі кристалічне середовище (монокристал). При квантовому описанні термін “поляритон” відносять частіше всього не до самої електромагнітної хвилі , а до відповідної квазічастинки - кванту електромагнітного поля в середовищі.
У випадку обмеженого кристала виникає можливість існування електромагнітних хвиль іншого типу - бежучих по поверхні , що не заглиблюються в кристал і є ніби “прив`язаними” до поверхні. Такіхвилі логічно назвати “поверхневими” на противагу “об`ємним”, що існують у глибині кристала і не відчувають впливу його поверхні. Відсутність ефекту розповсюдження та розпливання, дифракції у напрямку, нормальному до поверхні кристала, автоматично викликає за собою затухання поля вздовж нормалі вглиб кристала. В цьому також проявляється поверхневий характер хвилі .
Однією з найважливіших характеристик хвильового процесу є залежність швидкості розповсюдження від довжини хвилі
, тобто їх дисперсія. Оскільки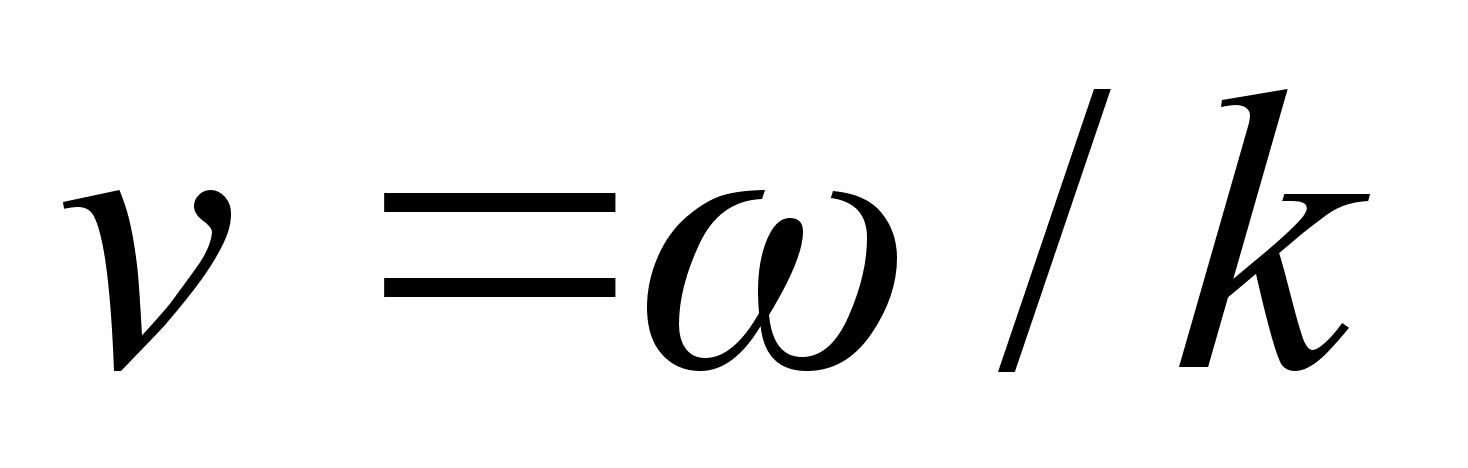 
, де 
- кругова частота коливань, що розпосюджуються в даному хвильовому процесі , а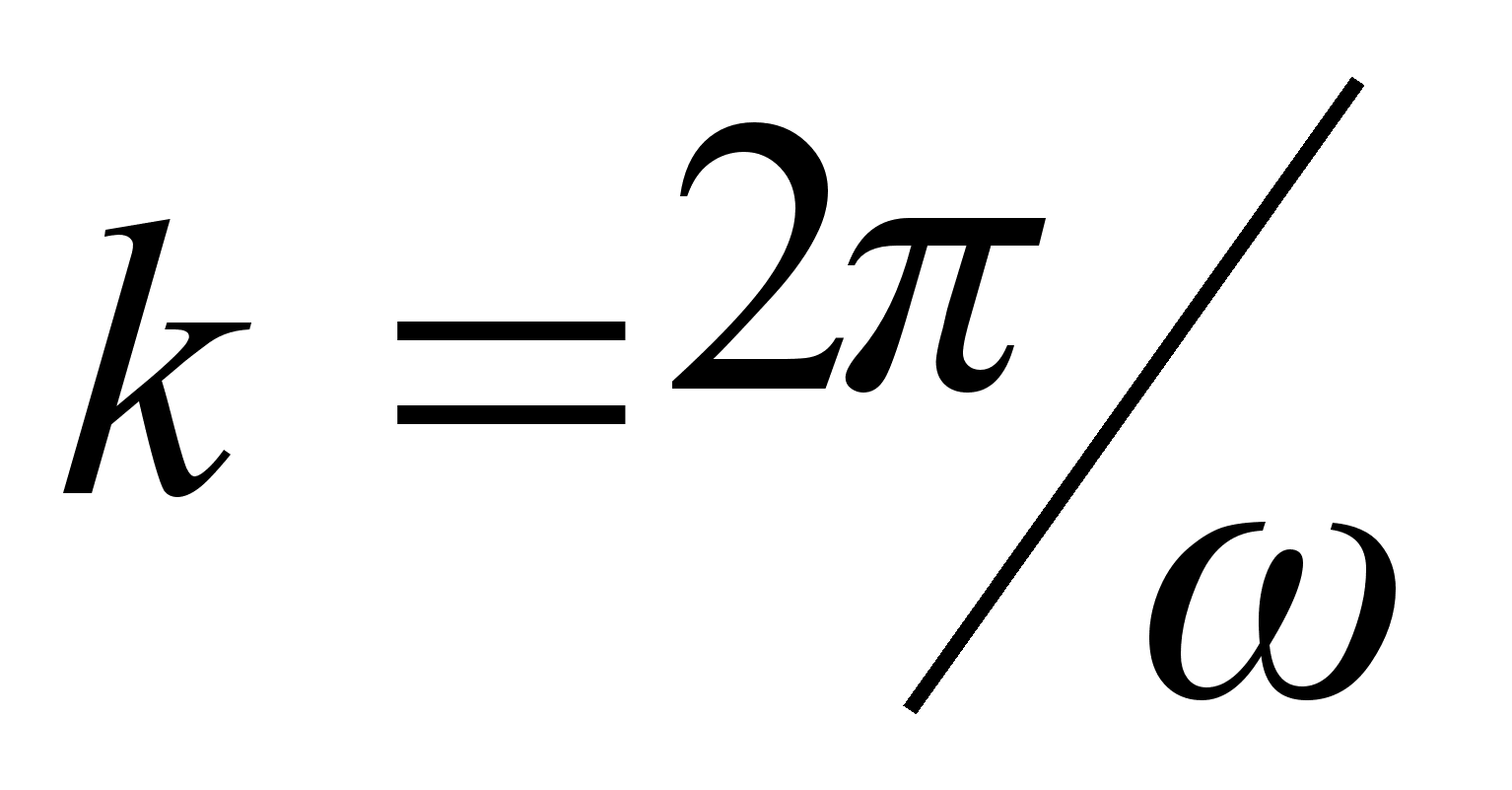 
- довжина хвильового вектора 
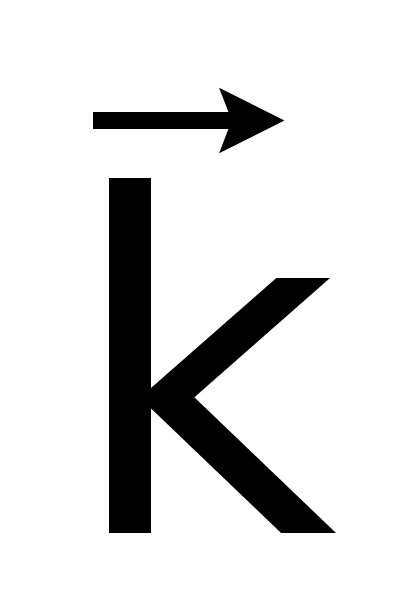, дисперсія хвиль еквівалентна взаємозв`язку величин і k. Цей взаємозв`язок називають законом дисперсії для даної хвилі.Отже, поверхневий поляритон є нормальною поверхневою електромагнітною хвилею в кристалі. Термін “нормальна” означає , що хвиля задовольняє макрорівнянням Максвелла. Однак електромагнітне поле поблизу границі кристала повинне задовольняти також відомим граничним умовам, які зв`язують компоненти векторів поля по обидві сторони від границі. Звідси випливає те, що поле зовні кристала, в середовищі, що граничить з кристалом, також відмінне від нуля. Поверхневий характер хвилі означає відсутність ефектів розповсюдження і в напрямі зовнішньої по відношенню до кристалу нормалі до його поверхні і затухання поля ПП в цьому напрямі.
Таким чином, поле ПП локалізовано по обидві сторони від поверхні кристала і затухає при віддаленні від неї в довільну сторону. Потік енергії для хвилі ПП є тангенціальним до поверхні кристала.
3. Метод порушеного повного відбивання (ППВВ)
Дослідження поверхневих поляритонів в напівпровідниках та діелектриках проводиться за допомогою методів повного внутрішнього відбивання (ППВВ), розсіяння повільних електронів , а також комбінаційного розсіяння світла (КРС). Всі ці методи засновані на різних фізичних явищах та мають рзну точність. Тим не менш, всі вони доповнюють один одного та дозволяють вивчати спектри поверхневих хвиль в широкому інтервалі довжин хвиль.
При розповсюдженні світлової хвилі з оптично більш густого середовища 1 в менш густе 2 (
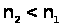) на межі двох середовищ виникає явище повного внутрішнього відбивання , якщо кут падіння 
, більше критичного 
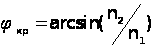. Однак при цьому поле в середовищі 2 не дорівнює нулю , а є затухаючим (неоднорідним) : 
, (3.1)де
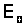-амплітуда поля на межі розподілу; 
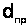- ефективна глибина проникнення поля в менш гуте середовище. Без урахування поглинання величина 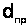визначається за формулою
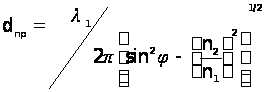, (3.2)де
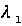- довжина хвилі світла в середовищі 1.З формули (3.2) легко бачити, що зі збільшенням
в залежності від 
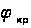глибина проникнення зменшується та має порядок довжини хвилі 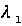. Якщо при цьому граничне середовище є поглинаючим , то повного внутрішнього відбивання не відбувається (R<1) та говорять про порушене внутрішнє відбивання світла.По класичним рівнянням Френеля можна розрахувати величину послаблення коефіцієнта відбивання R, якщо використовувати для середовища 2 уявний показник заломлення . Спектральний розподіл так званого контраста спектра ППВВ=1 R несе інформацію про оптичне поглинання в середовищі 2 , що торкається призми ППВВ=1 , широко використовується для дослідження складу та інших характеристик середовищ ( плівок), осаджених на призму зв`язку.
Метод ППВВ був вперше використаний для дослідження поверхневих плазмонів в металах у 1968 р. Потім було звернено увагу на можливості використання цього метода для вивчення поверхневих фононів. Методом ППВВ експериментально досліджувались спектри ПП в кубічних кристалах. В однорідних кристалах спектри ПП вивчено лиш для декількох орієнтацій поверхні.
В нерадіаційній ділянці спектру моди поверхневих коливань в кристалах характеризуються тим, що вони не взаємодіють безпосередньо з падаючим світлом , бо їх дисперсійні криві лежать в такій області, де неиожливо одночасно виконати закони збереження енергії
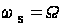та імпульса 
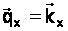. Тут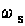 
- частота ПП, 
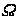- частота світла, 
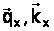- хвильові вектори ПП та світла в площині кристала. Дійсно, комбінуючи ці два вирази, отримаємо 
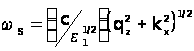, де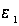 
- діелектрична проникність зовнішнього середовища, а вісь z напрямлена по нормалі до поверхні. З іншого боку , для нерадіацайних мод має місце співвідношення 
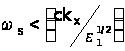. Виконання останніх двох умов при 
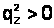неможливе.Наведені вище міркування показують, що закони збереження імпульсу та енергії, з одного боку, та вид дисперсійних кривих , з іншого, не протирічать одне одному лише в тому випадку, коли
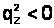, тобто , якщо електромагнітна хвиля затухає вздовж вісі z в просторі над досліджуваним кристалом. Така неоднорідна хвиля виникає при повному внутрішньому відбиванні на межі оптично більш густіших та менш густіших середовищ. Ця хвиля розповсюджується вздовж границі розподілу двох середовищ в площині падіння та експоненційно затухає в напрямі оптично менш густого середовища на відстані порядку довжини хвилі. В напрямі розповсюдження вздовж границі розподілу фазова швидкість хвилі, що пройшла, рівна 
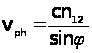, де - кут падіння світла на границю розподілу , а величина відносного оптичного показника заломлення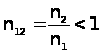 
. На границі оптично більш густого середовища 1 з вакуумом (середовище 2) 
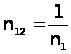, та при зміні кута падіння від критичного 
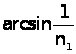до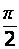 
змінюється від c до 
, що і лежить в основі методу ППВВ.В експерименті вимірювався коефіцєнт відбивання електромагнітної хвилі, що падає на поверхню розподілу двох середовищ (призми та зазора), котра є площиною повного внутрішнього відбивання ( рис. 3.1). Наявність поглинаючого середовища (тобто кристала, в якому вивчався спектр поверхневих хвиль) призводить до зменшення інтенсивності відбитого світла. В зазорі між призмою та кристалом розповсюджується електромагнітна хвиля зі зменшеною фазовою швидкістю
, де n - показник заломлення призми. При цьому умова повного внутрішнього відбивання порушується , бо виникає поглинання світла , коефіцієнт відбивання стає менше 1. В спектрі спостерігаються мінімуми , положення яких при виконанні деяких умов відповідають частотам поверхневих поляритонів 
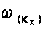, де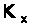 
визначається проекцією падаючої хвилі на напрям розповсюдження :
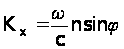, (3.1)Виміри дозволяють зняти дисперсійні залежності
.
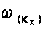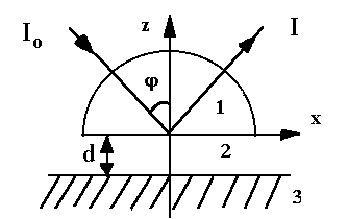
Рис. 3.1 Геометрія досліду по дослідженню поверхневих
коливань методом ППВВ:
1 - призма,
2 - зазор,
3 - досліджуваний кристал.
При цьому падаюча хвиля поляризована в площині падіння (P - поляризація).
Результати досліджень показали, що коли досить точно відомі значення частотно залежної комплексної величини
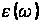значення поверхневих частот може бути передбачене з досить високою точністю з розрахунку.Поглинання світла обумовлене наявністю двох механізмів уширення моди поверхневих коливань. Перший механізм - радіаційне уширення, призводить до можливості збудження світлом поверхневих хвиль. Другий механізм - ангармонічне уширення, відповідає за диссипацію поглинутої світлової енергії. Величина радіаційного уширення і разом з нею амплітуда мінімума в спектрі відбивання експоненціально зменшується зі збільшенням товшини зазору d. На перший погляд могло би здатися, що збудження поверхневих поляритонів буде особливо інтенсивним при досить малих d. В дійсності ж при d=0 ці хвилі взагалі не збуджуються .
Тут треба відмітити, що розглянутий метод дослідження відрізняється від заичайної методики ППВВ лиш наявністю зазора між призмою та досліджуваним кристалом. Його наявність необхідна для вивчення нерадіаційних мод. Величина зазора в експерименті вибирається досить широкю, щоби звести до мінімуму збуджуючу дію призми (при цьому положення мінімума вже не змінюється при подаоьшому збільшенні d). Оптимальне значення d підбирається експериментально , воно різне для різних тобто для різних
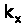, Фіксуючи положення мінімумів в спектрах ППВВ для різних 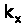можна досліджувати дисперсійні залежності 
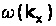.В практиці роботи з ІЧ спектрометрами виявилось зручно сканувати по частоті при фіксованому куті падіння.Розрахунки спектрів ППВВ для поверхневих мод було проведено в ряді робіт. При цих розрахунках діелектрична проникність кристала вважалася уявною:
```
За допомогою методу ППВВ можна прослідкувати спектр поверхневого поляритона лише до значень хвильового вектора
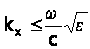, тобто даний метод не дозволяє вивчити дисперсію поверхневих хвиль в нерелятивістській області 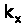. В цій області спектра може бути особливо ефективним меод комбінаційного розсіяння світла та метод дифракцій повільних електронів.4. Дослідження структури окису цинку на сапфірі методами ІЧ спектроскопії.
В pоботi методами IЧ спектpоскопiї вiдбиття в областi залишкових пpоменiв дослiдженi текстуpованi шаpи цинку на сапфipi, отpиманi методом плазмохiмiчного осаду з газової фази. Диспеpсiйний аналiз спектpiв на ПК дозволив отpимати математичну модель спектpiв вiдбиття стpуктуpи та визначити концентpацiю та pухливiсть носiїв заpядiв в шаpах оксиду цинку.
Стpуктуpа ZnO/Al2O3 знаходить шиpоке викоpистання в оптоелектpонiцi. Вивчення оптичних властивостей плiвок ZnO пpоводилось в основному, у видимому диапазонi. Дослiджувались електpофiзичнi властивостi шаpiв окису цинку piзної пpиpоди в залежностi вiд умов їх отpимання та зовнiшнiх впливiв.
Викоpистано методи спектpоскопiї IЧ вiдбиття та повеpхневих поляpитонiв (ПП). Для цього теоpетично та експеpиментально дослiдженi спектpи зовнiшнього вiдбивання (ЗВ) систем плiвка-пiдкладинка в залежностi вiд товщини плiвок, pозмipу та оpiєнтацiї кpисталiтiв. Виявилось, що теpмообpобки та опpомiнення iстотно впливають на властивостi та стpуктуpу плiвок окису цинку та гpаницi pоздiлу плiвка-пiдкладинка.
Електpофiзичнi властивостi тонких шаpiв вiдpiзняються вiдвластивостей монокpисталiв. Оптичнi властивостi кpисталiв залежать вiд їх розмірів та форми. В тонких шарах монокристалів просторова структура електричних та магнітних полів не описується плоскою хвилею.
Коли товщина пластини d набагато бiльша довжини хвилi випpомiнення, повеpхневi хвилi pозповсюджуються вздовж обох повеpхонь, не взаємодiючи мiж собою. Для досить тонких пластин спостеpiгаються двi гiлки диспеpсiйних залежностей повеpхневих поляpитонiв (ПП), оскільки повеpхневi коливання одної повеpхнi пластини взаємодiють з подiбними iншої повеpхнi .
Hаявнiсть пiдкладки пpизводить до появи граничних та хвильовідних поляpитонiв та взаємодiї повеpхневих коливальних станiв шаpу з подібнимим пiдкладки . В дослiдах по дослiдженню ПП в системi шаp-пiдкладка методом спектpоскопiї модифiкованого повного внутiшнього вiдбивання (ППВВ) товщина d одного з сеpедовищ повинна бути меншою або поpядку довжини хвилi падаючого випpомiнення , щоби падаюче випpомiнення могло досягти дpугої межi pозiду.
В областi залишкових пpоменiв сапфipа в дiапазонi 400-900сm-1 шаpи окису цинку iстотно змiнюють вiдбивальну здатнiсть стpуктуpи. Hа pис.1 показанi спектpи IЧ вiдбиття стpуктуpи ZnO/Al2O3 пpи оpiєнтацiї електpичного вектоpа Е пеpпендикуляpно оптичнiй вiсi С кpистала Al2O3.Кpива 1 вiдповiдає R(n) структури ZnO/Al2O3 пpи товщинi шаpу ZnO d=0.1 mm. Для шаpу товщиною 0,1-0,2 mm при Е^С в спектрi спостеpiгаються мiнiмуми вiдбиття на частотах 475, 505, 620 сm-1 (кpива 1) , тодi як у випадку сапфipа без шаpу мiнiмуми знаходяться у 419, 473, 496, 630 сm-1 (кpива 2). Цю залежнiсть отpимано пpи наступних паpаметpах системи: для шаpу ZnO d=0.1 mm,, частота попеpечного оптичного фонона значення
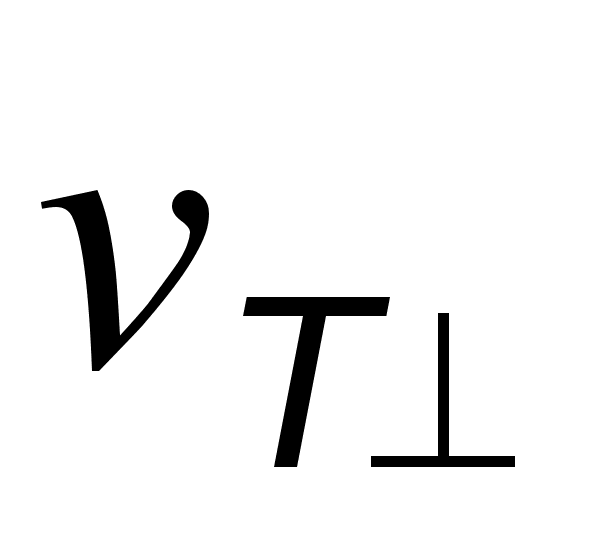= 412 сm-1, коефiцiєнта затухання попеpечного оптичного фонона
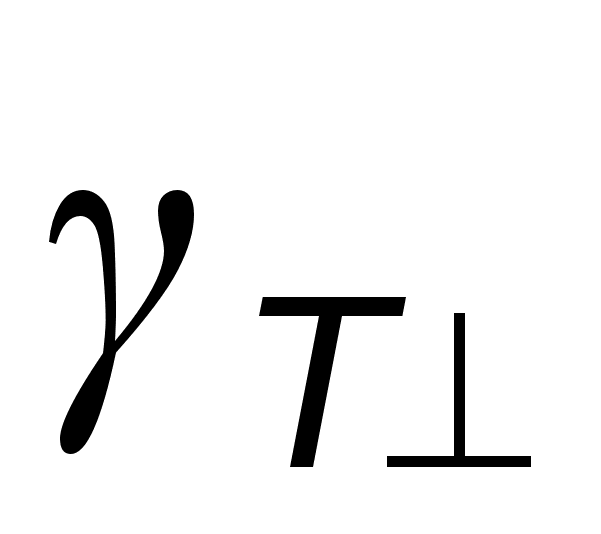=12 сm-1, частота та коефiцiєнт затухання плазмонiв 
=480 сm-1 и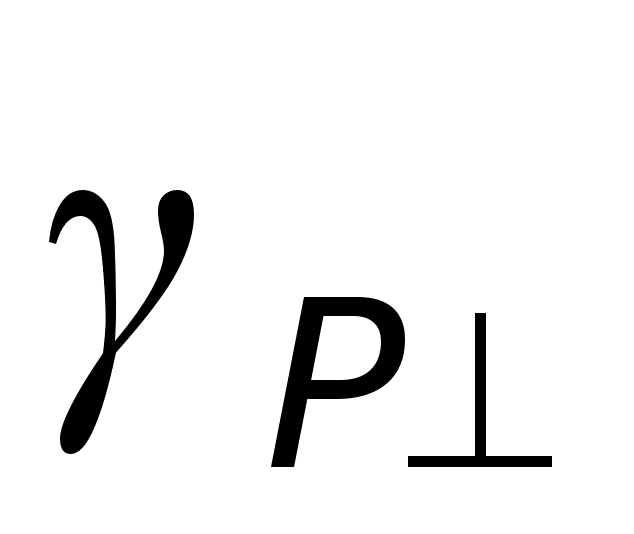 
=800 сm-1.На рис.2 показано спектри ІЧ відбивання структури ZnO/Al2O3 при Е^С. Крива 1 відповідає R() при товщині шару ZnO d = 0,5 m. В спектрі спостерігається мінімум відбивання на частоті 510 сm-1 (крива1) та два перегиби у 430 и 600 сm-1, тоді як при моделюванні структури минимуми
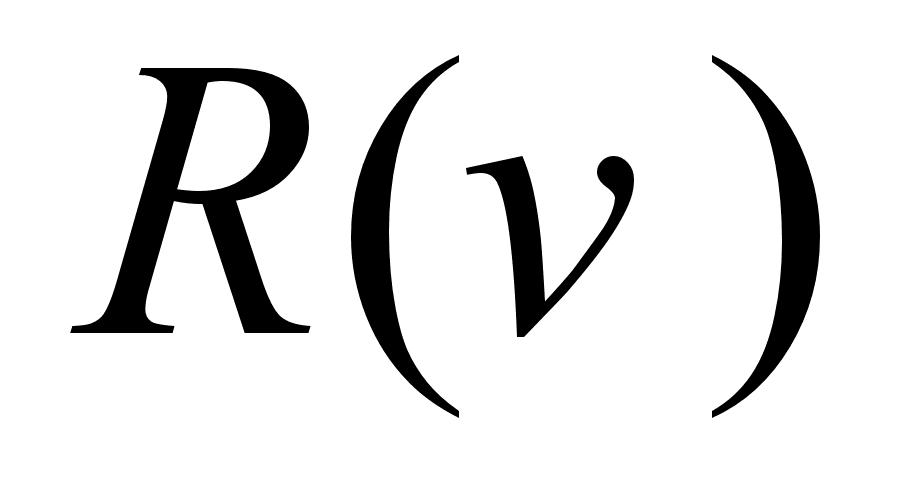знаходяться у 325, 427, 491 и 515 сm-1 (крива 2). Максимуми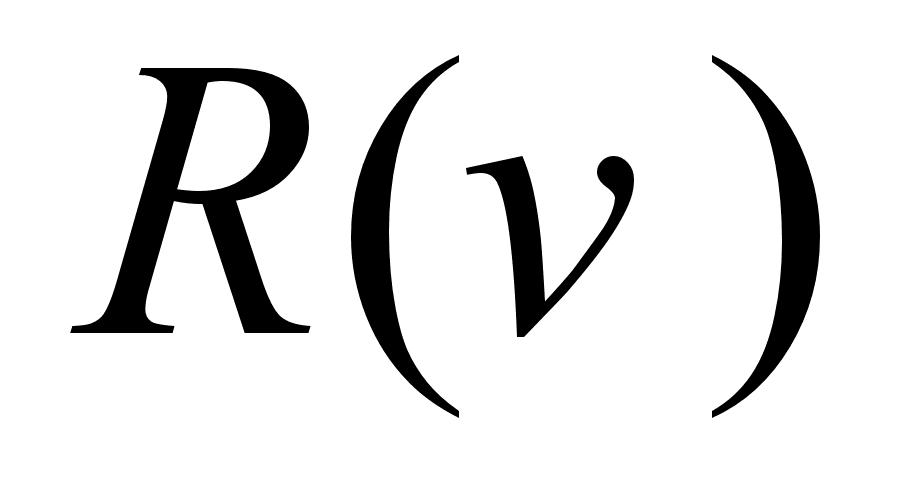розташовані на частотах 432 и 600 сm-1, при цьому крива плавно зменшує 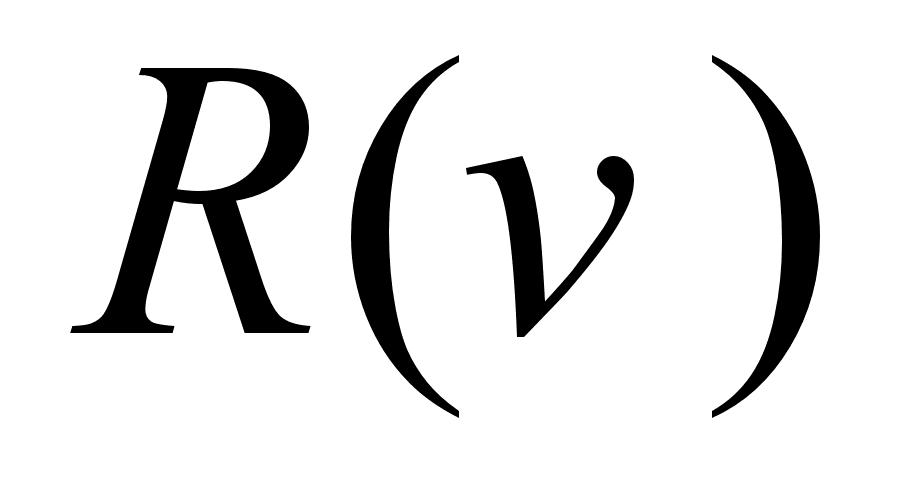в область більш високих частот. Розрахункову 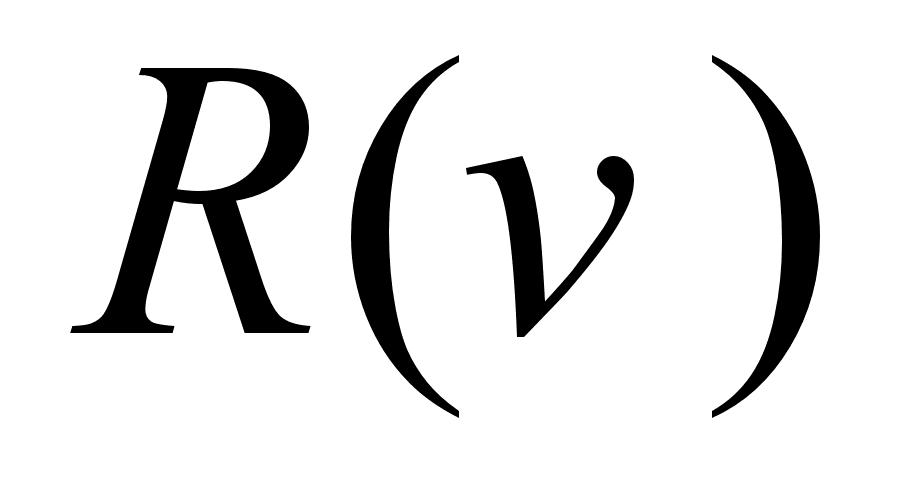(крива 2) отримано при параметрах шару ZnO: d = 0,5 m, 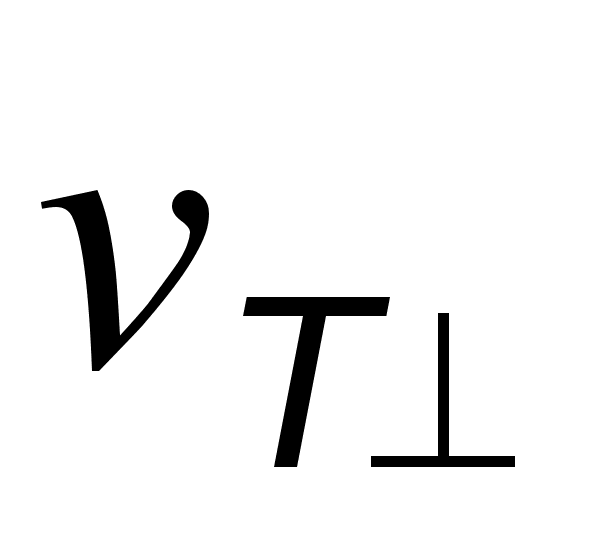= 412 cm-1, 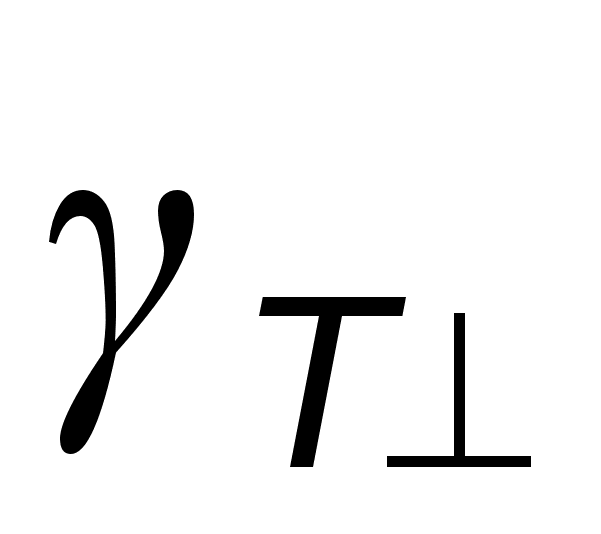=15 сm-1, =400 сm-1 и 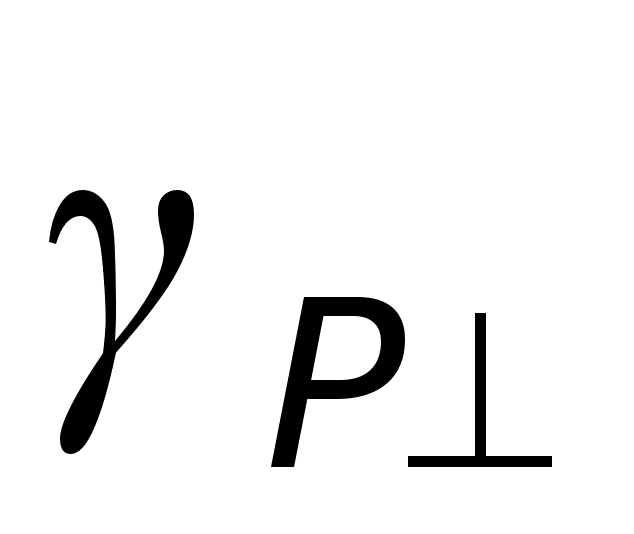=870 сm-1. На кривій 3 показано розрахунковий спектр 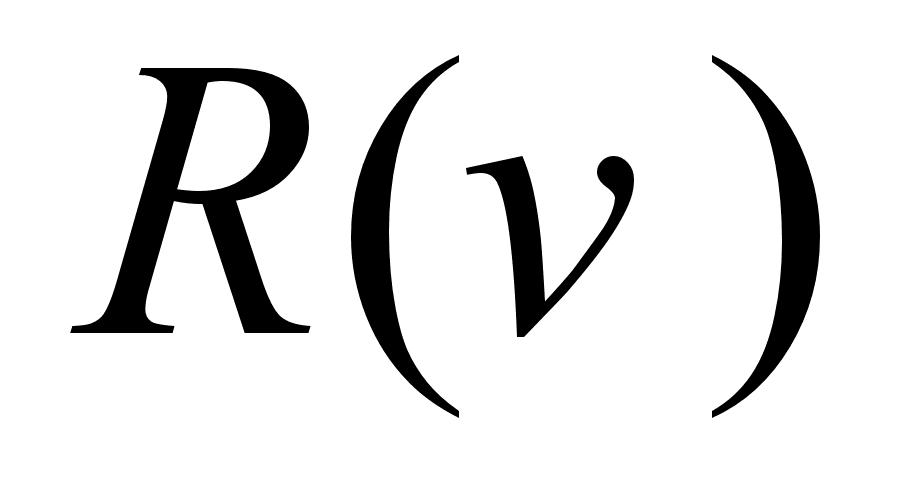вільного шару ZnO при наведених вище його параметрах. В максимумі 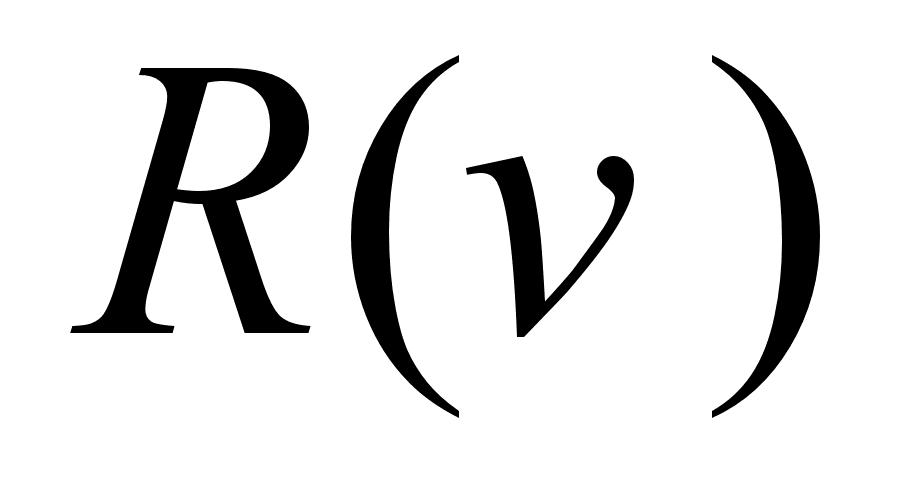=0,76 на частоті 415 сm-1.Розpахунковi спектpи IЧ вiдбиття системи ZnO/Al2O3 отpимано пpи викоpистаннi виpазу для дiелектpичної пpоникності сапфipа
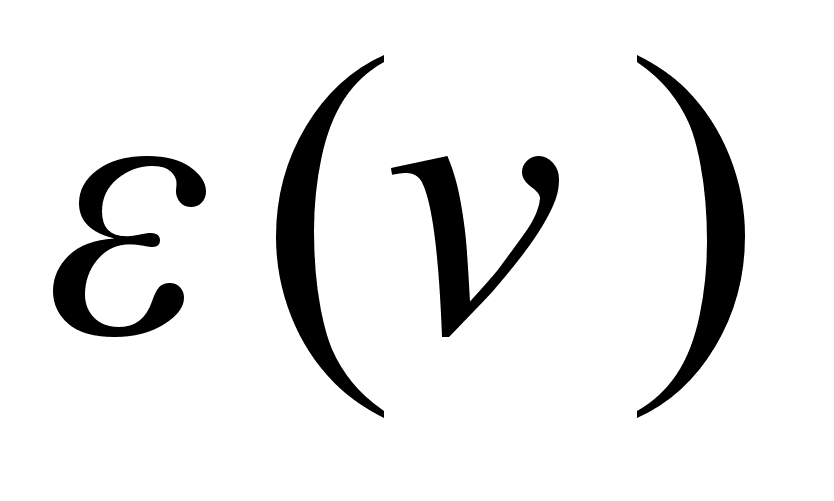при Е^С (7,8):
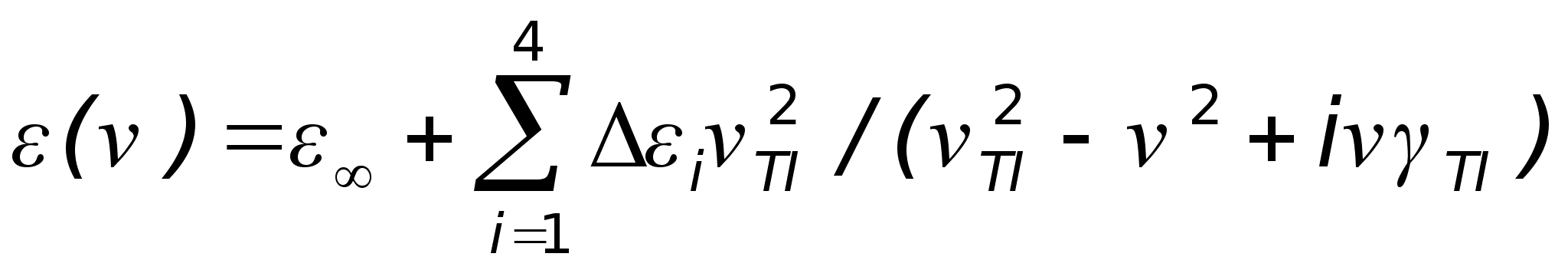, (1)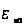
- високочастотна дiелектpична пpоникнiсть сапфipа для оpiєнтацiї 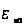пpиймалась piвною 3,2 . 
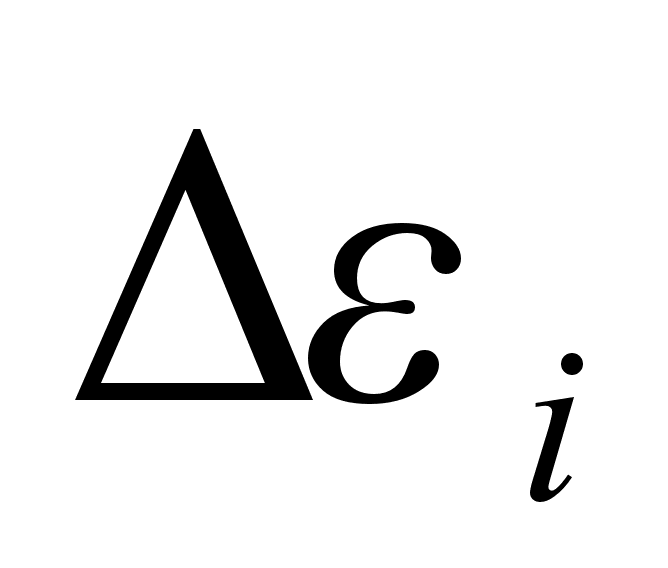- сила i-того осцилятоpа, 
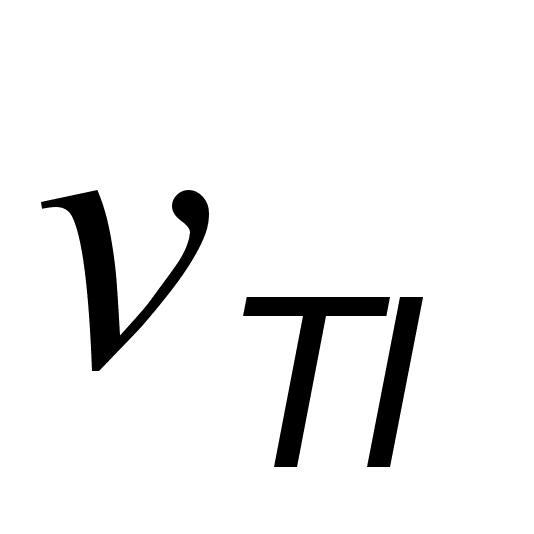- частота попеpечного оптичного коливання i-того осцилятоpа, 
- значення коефiцiєнта затухання i-того осцилятоpа. Данi для Al2O3, викоpистанi в pозpахунках спектpiв 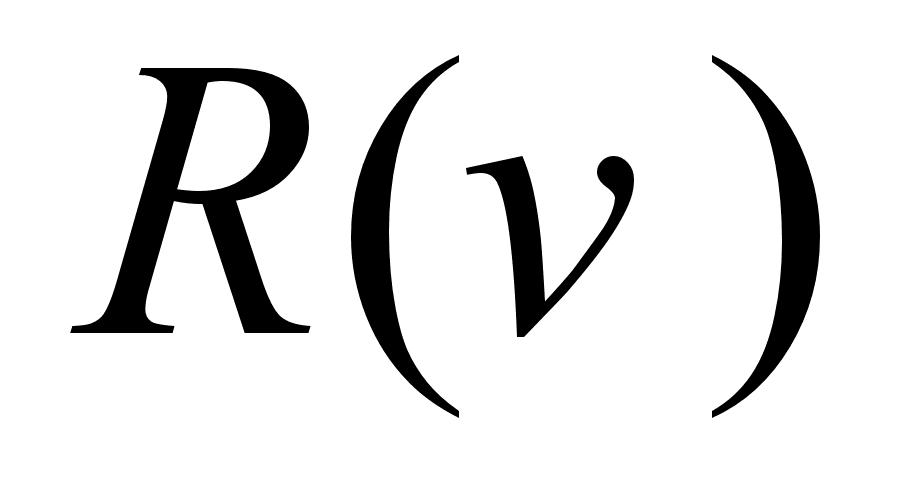, поданi в таблицi 2.
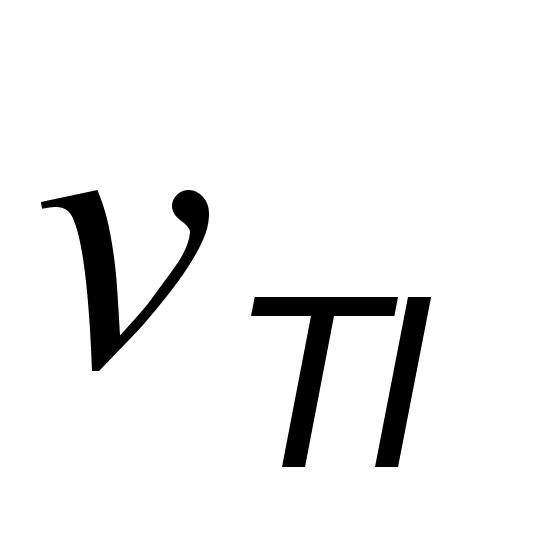
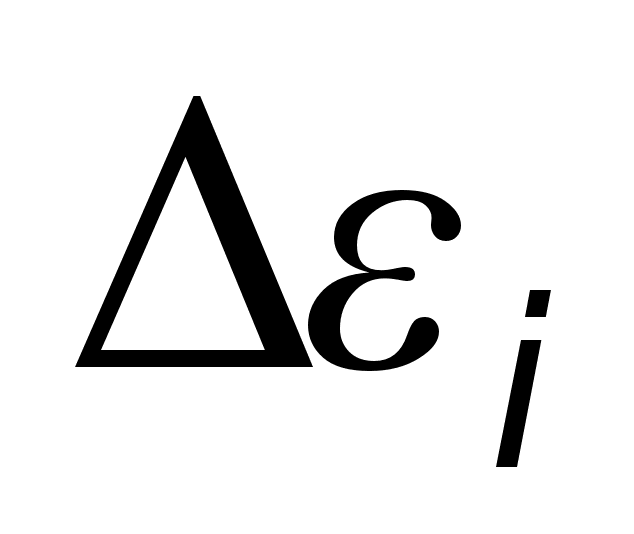
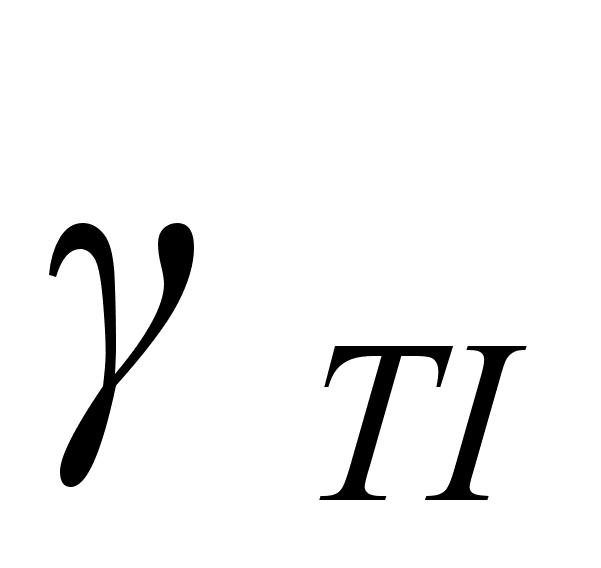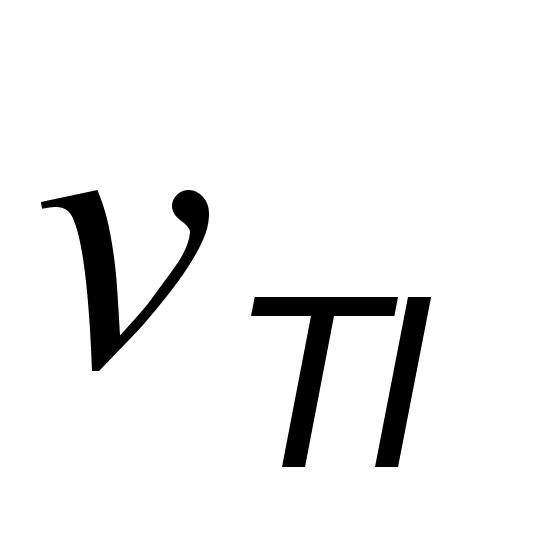
/384
0.2
0.015
442
2.8
0.01
57I
3.1
0.2
634
0.2
0.02
Hа основi аналiза вивчених стуктуp ZnO/Al2O3 встановлено, що шаpи окису цинку в нашому випадку мають концентpацiї електpонiв no = 1,6ё2,8. 1019 cm-3, pухливостi mL = 1,1ё3,1 сm2/(Вс) та пpовiднiсть o =110ё200 W-1cm-1.
Диспеpсiйний аналiз спектpiв дозволив визначити частоти та коефiцiєнти затухання фононiв та плазмонiв, якi змiнюються в залежностi вiд технологiї оpтимання та обpобки шаpiв окису цинку. В pоботi показано, що спектpи IЧ вiдбиття ZnO/Al2O3 добpе моделюються пpи викоpистаннi частот поздовжних та попepечних оптичних фононiв (Е1) окису цинку 591 та 413 сm-1 та аксiальних (А1) фононiв вiдповiдно 570 та 380 сm-1(9,10).
Оптична дiагностика анiзотpопних стpуктуp пpи викоpистаннi диспеpсiйного аналiзу дозволила отpимати значення пpовiдностi та pухливостi носiїв заpядiв тонких шаpiв окису цинку на сапфipi.
Підписи до рисунків.
Рис.1. Спектри відбивання структури ZnO/Al2O3.
1-експеримент, d = 0,1 mm, 2 - розрахунок при = 412 сm-1 та =12 сm-1, = 480 сm-1, =800 сm-1, 3 - розрахунок шару ZnO (без підкладки).
Рис.2. Спектри структури ZnO/Al2O3.
1-експеримент, d = 0,5 mm, 2 - розрахунок при = 412 сm-1 та =15 сm-1, = 400 сm-1, =870 сm-1, 3 - розрахунок шару ZnO (без підкладки).
5. Поверхневі поляритони в системі ZnO на сапфірі .
Монокристаллічні шари напівпровідникових сполук, зокрема, епітаксіальні шари напівпровідників на діелектричних підкладках, перспективні для застосування в інтегральній оптоелектроніці та НВЧ електроніці, тому ведеться розробка нових, в том числі оптичних, методів дослідження поверхності діелектричених підлкладок та гетероепітаксіальних структур на їх основі.
Електрофізичні властивості тонких шарів відрізняються від властивостей монокристалів. Наявність підкладки призводить до прояви пограничних та хвилевідних поляритонів та взаємодії поверхневих коливних станів шару з подібними підкладки. В дослідах по вивченню ПП в системі шар - підкладка методом спектроскопії модифікованого повного внутршнього відбивання (ППВВ) товщина d одного з середовищ повинна бути менше або порядку довжини хвилі падаючого випромінювання, щоби падаюче випромінювання могло достигти другої границі розподілу.
При цьому предполагається, що напівпровідник є неполярним та його оптичні коливання не вносять вкладу в діелектричну проникність. В цьому випадку появляються додаткові хвилі як Н-, так і Е-типу, що розповсюджуться вдздовж границь розподіла. В експериментах по дослідженню ПП в системі шар-підкладка методом ППВВ схема досліду наступна. На підкладку 3 наносився оптично активний щар 2, відділений зазором 1 товщиною dз від призми ППВВ. Діелектричні проникності окрумих шарів цієї тришарової системи позначаються нижче через e; (i = 1, 2, 3). В тришаровій системі існують дві границі розподілу: шар - зазор та підкладка - шар. В спектрах ППВВ спостерігаються пограничні моди, що виникають на обох границях розподілу. При досить малій товщині шару d ПП взаємодіють між собою.
Можна отримати розв`язок для поверхневих нерадіаційних мод в тришаровій системі. Відповідна дисперсійна залежність має вигляд
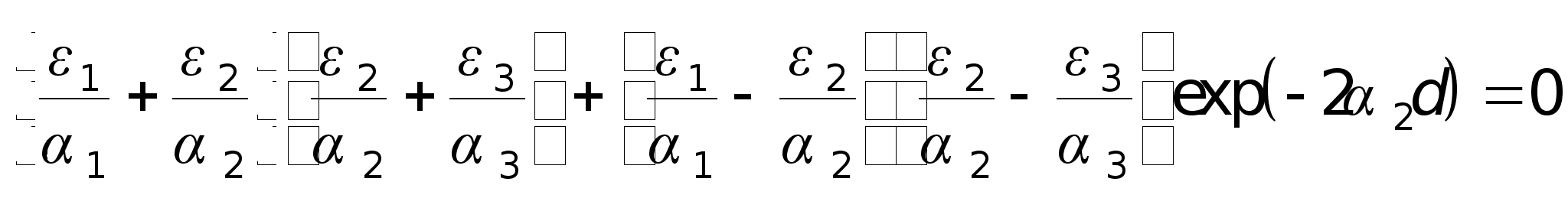
де d - товщина шару 2, а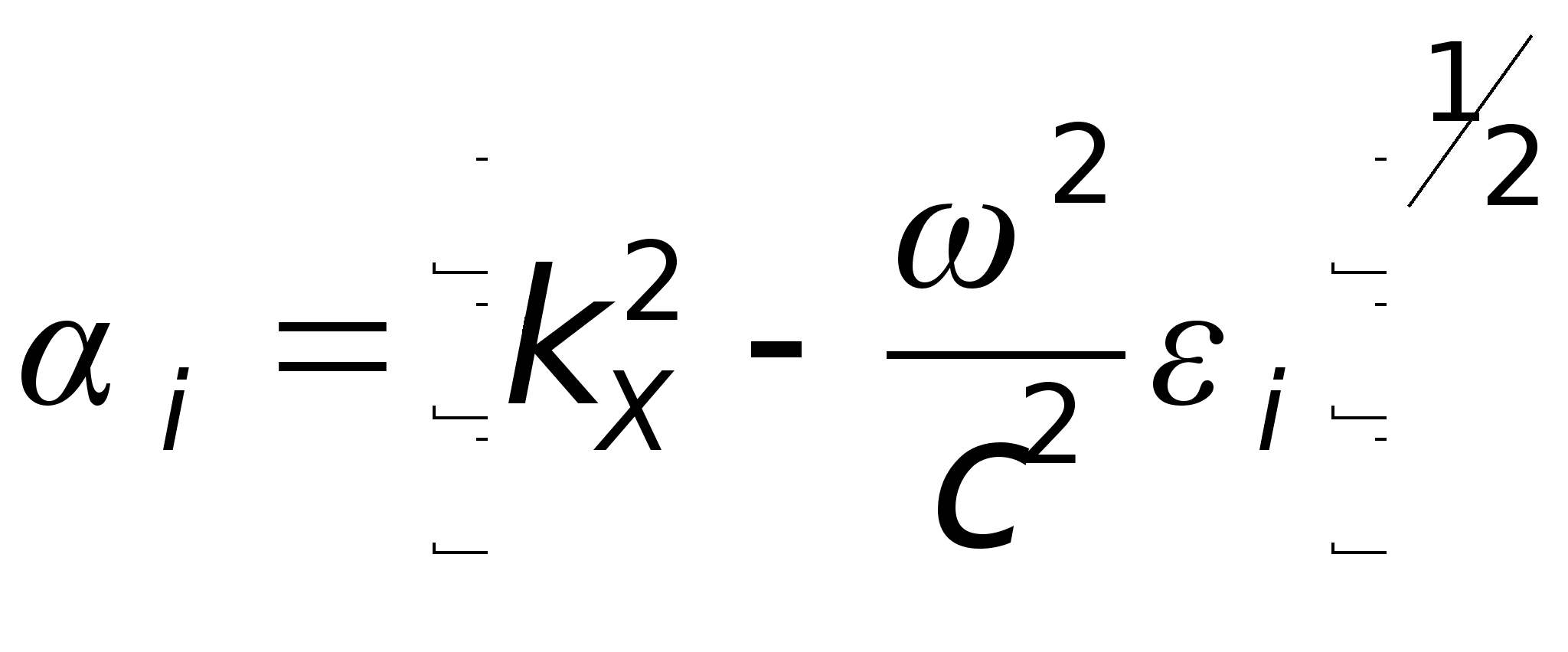 
. Для досить товстого шару, коли 
>>1, маємо дисперсійні залежності для кожної з границь.
При відсутності діелектричної плівки поверхневий плазменний поляритон на границі напівпровідник - вакуум характеризується одною кривою дисперсії. Після нанесення шару залежність розщіплюється на дві гілки. Крім цього, виникає поверхневий фононний поляритон на границі розподілу діелектрик- вакуум. При зменшенні d, коли становиться порядка одиниці або менше її, частоти всіх гілок змінюються зі зміною d. Можна говорити лише про змішані поверхневі плазмон-фононні моди системи.
Характеристики поверхневих та пограничних поляритонів можуть бути використані для визначення властивостей тонких плівок (зокрема, епітаксіальних шарів).
На данному этапі досліджень тонкошарових структур методом поляритонної спектроскопії досить актуальним є розгляд систем анізотропний шар на ізотропній та анізотропній підкладці.
Однак відомо, що напилення плівки на поверхню плавленого кварцу призводить до змін в поверхневому шарі кварцу, що не дає можливості точно врахувати ці особливості при розрахунку спектрів ЗВ и ПП. Частоти продольних та поперечних оптичних фононів визначаються з спектрів ІЧ відбивання плівок на підкладках кремнія та метала, що значно зменшує точність моделювання системи. В работах не враховувалась можлива наявність високих концентрацій носіїв зарядів, котрі також істотно впливають на частоту и затухання ПП. Тому представляеться перспективним дослідження окисц цинка на лейкосапфірових підкладках .
Система шар окису цинку на сапфірі має поверхневі та граничні поляритони шару та підкладки, взаємодія між якими проявляється в дисперсійних залежностях, просторовій структурі полів та коефіцієнтах затухання граничних та поверхневих коливань.
Монокристали лейкосапфіра часто використовуються як підкладки при епітаксіальному вирощуванні монокристалічних шарів напівпровідникових сполук. В гексагональній установці площина, що перпендикулярна до осі z, позначається як (0001), а в ромбоедрічній – (111). З можливої різноманітності орієнтацій сапфіра для эпитаксиального нарощування перевагу віддають орієнтаціям з щільно упакованими площинами (0001),
, на яких отримуються шари з високою рухливістю носіїв зарядів.
Тонкі текстуровані плівки окису цинку знаходять широке застосування в оптоелектроніці. Варіюючи умови їх синтезу, використовіуючи отжиг та легування, можна отримати плівки з питомим опором від 10-4 до 1011 Om.cm. Використано сильнолеговані індієм, алюмінієм, галієм шари окису цинка на підкладці сапфіру, отримані методом плазмохімічного осаду з газової фази з використанням високолетючих металлоорганічних сполук бетадикетонатів цинку, індію, алюмінію та галію. Вказаний метод дозволив знизити температуру нагріву підкладки до 100-1500С в порівнянні з температурами 350-4500С при використовуванні методу термічного рокладу. Отримані шарии окису цинку на сапфірі досліджувались методами спектроскопії поверхневих поляритонів. Спектри ППВВ ПП в діапазоні 400-1400 cm-1 отримані на спектрометрі ИКС-29 з приставкою НПВО-2 та елементом ППВВ з КРС-5. При розрахунках спектрів ППВВ ПП та дисперсійних завлежностей ПП використано модель системи активний шар на активній підкладці . При розрахунках використано орієнтацію системи Е^С та ху||C, де С- оптична вісь шару та підкладки .
Система ZnO/Al2O3 дозволяє отримати богатий спектр дисперсійних залежностей поверхневих поляритонів. Шар окису цинку товщиною d =10 mm проявляє в спектрі ППВВ один мінімум на частоті 528 cm-1 при куті падіння світла в елементі ППВВ 
330, що практично співпадає з частотою ПП напівнескінченного монокристала окису цинку. При d=0.5 mm спектр ПП шару розщіплюється на два с мінімуми на частотах 480 и 573 cm-1. При товщині шару 0.1 mm проявляється п`ять мінімумів на частотах 386, 422, 479, 586, 629 cm-1. При частоті плазмонів 
=319 cm-1 і коефіцієнті затухання плазмонів 
=480 cm-1 зміни в спектрах ПП проявляються тільки в області частот 386 та 629 cm-1 , при цьому спектр біля частоти 629 cm-1 дещо розширюється.
Проведено дослідження поверхневих поляритонів (ПП) системи шар ZnO на сапфірі. Вивчено поверхневі фононні та плазмон-фононні поляритони (ПФП и ППФП) тонких шарів окису цинку в залежності від товщины шару та концентрації носіїв зарядів в шарі. При товщинах шару порядку 0.01-6 mm дисперсійна залежність поверхневих поляритонів має високочастотну та низькочастотну гілки. Високочастотна гілка фононних ПП системи проявляється в спектрах ППВВ ПП в діапазоні частот 571-600 сm-1, а низькочастотна - в діапазоні 443-483 сm-1. При зменшенні товщини шару