Майкельсон Альберт Абрахам

Майкельсон (Michelson) Альберт (19.XII.1852–9.V.1931). Американский физик. В 1878–82 и 1924–26 провел измерения скорости света, долгое время остававшиеся непревзойденными по точности. В 1881 экспериментально доказал и совместно с Э. У. Морли (1885–87) подтвердил с большой точностью независимость скорости света от скорости движения Земли. Эти работы явились экспериментальным обоснованием специальной теории относительности. В своем опыте Майкельсон применил изобретенный им интерферометр, с помощью которого в 1892–93 провел измерения спектральных линий различных элементов. Предложил в качестве эталона длины взять длину волны красной линии кадмия. Построил спектральный прибор сверхвысокой разрешающей силы. В последние годы жизни занимался определением угловых диаметров звезд, для чего создал звездный интерферометр. Нобелевская премия (1907) за созданные им оптические приборы и проведенные с их помощью исследования.

I. Жизнь и творчество А.А. Майкельсона

МАЙКЕЛЬСОН, АЛЬБЕРТ АБРАХАМ (Michelson, Albert Abraham) (1852–1931), американский физик, удостоенный в 1907 Нобелевской премии по физике за создание прецизионных инструментов и выполненные с их помощью спектроскопические и метрологические исследования.

Альберт Майкельсон родился 19 декабря 1852 года в польском местечке Стрельно, принадлежавшем в то время Германии (ныне Стшельно, Польша). Когда ребенку исполнилось два года, семья эмигрировала в Америку. Отец Альберта, Сэмюэль Майкельсон, владевший в Стрельно небольшим галантерейным магазином, сначала работал ювелиром в Нью-Йорке, затем переехал с семьей к своей сестре в Калифорнию. Это был период калифорнийской "золотой лихорадки". Толпы золотоискателей и веселых бродяг, шумных торговцев и отчаянных головорезов составляли население "лагеря Мэрфи", где Сэмюэль открыл маленькую галантерейную лавочку. Однажды в лавку зашел бородатый золотоискатель с черным футляром под мышкой. Притаившийся в углу Альберт со страхом глядел на заросшее лицо незнакомца.

«Что ты так испугался, малыш?» - спросил золотоискатель: «Хочешь, я тебя развеселю?».

Бородач вынул из футляра скрипку и начал играть. Волшебные звуки очаровали мальчика. Золотоискатель оказался хорошим музыкантом. Он привязался к Альберту и стал учить его игре на скрипке, а тот старательно упражнялся и вскоре научился очень неплохо играть. В тринадцать лет мальчика определили в среднюю школу в Сан-Франциско. Директор поселил его в своем доме и быстро обнаружил у воспитанника незаурядные способности к механике. Они были настолько явными, что Альберту поручили ремонт нехитрого школьного оборудования, за что платили три доллара в месяц. После окончания школы на семейном совете было решено: надо поступать в Морскую академию. Она давала прекрасное образование, возможность блестящей карьеры и, что было немаловажно для небогатой многодетной семьи, государственное содержание со стипендией 500 долларов в год.

Новоиспеченный кадет успевал по всем предметам весьма средне, за исключением естественных наук и математики. Он занимался боксом, став "первой перчаткой" академии в легком весе, фехтованием, теннисом и рисованием. Отслужив два обязательных года морской службы на нескольких кораблях, Майкельсон получил предложение преподавать физику и химию в академии. И с радостью согласился.

В 1873 окончил Военно-морскую академию в Аннаполисе. После выпуска два года плавал на кораблях, а затем был назначен преподавателем физики той же академии. В это время началась научная деятельность Майкельсона.

Он словно проснулся. До этого его жизнь была цепочка довольно заурядных событий: служба, спорт, музыка, рисование... Женитьба в 24 года. Что его ждет дальше? Больше всего на свете его интересует физика, и особенно оптика.

Первым его успехом было повторение опыта Фуко по измерению скорости света, при этом точность полученных им результатов долгое время оставалась непревзойденной. В 1880–1882 он стажировался в университетах Берлина, Гейдельберга, Парижа. Работая в Берлине у Гельмгольца, заинтересовался проблемой обнаружения «эфирного ветра» и для проведения соответствующего эксперимента сконструировал интерферометр, названный впоследствии его именем. С его помощью провел измерения спектральных линий различных элементов, однако ответа на основной интересовавший его вопрос не получил из-за недостаточной точности установки. В 1883 вернулся на родину, до 1889 был профессором Школы прикладных наук в Кливленде. Здесь он провел важное исследование распространения света в сероуглероде, подтвердившее теорию Рэлея о связи между групповой и фазовой скоростями, а затем решил вернуться к опытам, начатым в Европе. Совместно с Э.Морли создал новый интерферометр, позволявший достичь необходимой точности, и в 1887 получил результат, который английский ученый Дж.Бернал назвал «величайшим из всех отрицательных опытов в истории науки». Этот опыт стал фундаментальным подтверждением специальной теории относительности. В 1889–1892 Майкельсон работал профессором университета Кларка в Вустере (шт. Массачусетс), затем до 1929 – профессором Чикагского университета. В 1890-е годы он решил важную метрологическую задачу: провел измерение эталона метра в единицах длины волны излучения кадмия. В эти же годы, заинтересовавшись звездной спектроскопией, изобрел спектральный прибор высокой разрешающей способности – «эшелон Майкельсона».

В 1920 с помощью изобретенного им «звездного интерферометра» провел измерения угловых размеров звезды-гиганта Бетельгейзе. В 1929 он повторил опыт Майкельсона – Морли, добившись еще более высокой точности. Последним его исследованием, завершить которое пришлось ученикам, стало новое измерение скорости света, но уже в вакууме.

В 1900–1903 Майкельсон был президентом Американского физического общества, в 1923–1927 – президентом Национальной академии наук США. Умер Майкельсон в Пасадене (шт. Калифорния) 9 мая 1931.

II. Об эфирном ветре

Создание Максвеллом теории электромагнитного поля поставило перед физикой новые задачи, одной из которых была проблема применимости принципа относительности, сформулированного Галилеем в XVII в., к электродинамическим явлениям. Решение этой проблемы, как указал сам Максвелл, могло быть получено при исследовании относительного движения Земли и «светоносного» электромагнитного эфира, который в теории Максвелла заменил упругий (механический) эфир Юнга – Френеля. Если бы существовал эфир, то его можно было бы принять за абсолютную систему отсчета, что означало бы отказ от принципа относительности. К моменту создания теории электромагнитного поля уже имелись наблюдения и эксперименты (наблюдения аберрации света, опыты Физо по исследованию распространения света в движущейся воде и др.), результаты которых позволили высказать определенные гипотезы о свойствах эфира. Однако непосредственные доказательства существования эфира мог дать только прямой эксперимент. Идею такого опыта сформулировал еще Максвелл, предложивший использовать в качестве движущегося тела Землю, которая перемещается по орбите со скоростью v ≈ 30 км/с. Однако Максвелл справедливо указал, что основная трудность в постановке этого эксперимента состоит в том, что он должен быть опытом «второго порядка», т.е. в нем требуется зафиксировать величину, пропорциональную квадрату отношения скорости Земли к скорости света с: v/c ≈ 10^–8 (это обстоятельство обусловлено замкнутостью пути света во всех подобных опытах, проводимых на Земле). Столь высокая точность, уникальная для экспериментальной физики XX в., была достигнута в опытах американских ученых А. Майкельсоном и Э. Морли.

История опыта Майкельсона – Морли изобилует интересными и поучительными эпизодами. Первый вариант интерферометра был построен немецкими мастерами в Берлине на средства, предоставленные изобретателем телефона американцем А. Беллом. Неудача европейского цикла исследований Майкельсона была связана с тем, что прибор оказался чрезвычайно чувствительным к вибрациям, которые не удавалось устранить даже при помещении его в глубокий подвал знаменитой Потсдамской обсерватории. Кроме того, в первом варианте интерферометра, где использовалась одна пара зеркал, оптическая длина пути световых лучей была слишком малой, вследствие чего ожидаемый эффект оказывался на грани точности измерений. К тому же в первой публикации, посвященной поиску «эфирного ветра», Майкельсон сделал одну довольно элементарную теоретическую ошибку...

При проведении опытов в США все эти обстоятельства были учтены, что резко повысило точность и достоверность результатов. Именно поэтому выводы Майкельсона и Морли остались незыблемыми и после множества повторений опыта, проведенных с конца XIX в. до наших дней.

III. Об относительном движении Земли и светоносного эфира

За открытием аберрации света вскоре последовало ее объяснение на основе эмиссионной теории. Эффект приписывался простому сложению скорости света со скоростью Земли на орбите. Трудностей этого кажущегося удовлетворительным объяснения не замечали до тех пор, пока не было предложено объяснения на основе волновой теории света. Это новое объяснение было поначалу столь же простым, как и предыдущее. Но оно оказалось бессильным перед экспериментально доказанным фактом, что аберрация не меняется, когда проводятся наблюдения с помощью телескопа, заполненного водой. Действительно, если тангенс угла аберрации равен отношению скорости Земли к скорости света, то, поскольку последняя скорость в воде составляет три четвертых скорости света в вакууме, аберрация, наблюдаемая с помощью телескопа, заполненного водой, должна составлять четыре третьих ее истинного значения. (Можно отметить, что большинство авторов считают удовлетворительным объяснение на основе эмиссионной теории света, хотя в действительности здесь трудностей даже больше, чем в случае волновой теории. Согласно эмиссионной теории, скорость света в телескопе с водой должна быть больше, а угол аберрации должен быть меньше; поэтому, чтобы свести его к истинному значению, мы должны принять абсурдную гипотезу, что движение воды в телескопе переносит лучи света в обратном направлении!)

Согласно Френелю, в волновой теории эфир, во-первых, предполагается находящимся в покое, за исключением внутренности прозрачных сред, в которых, во-вторых, он считается движущимся со скоростью, меньшей скорости среды в отношении (² – 1) / ², где – коэффициент преломления. Эти две гипотезы дают полное и удовлетворительное объяснение аберрации. Вторая гипотеза, несмотря на ее кажущееся неправдоподобие, должна считаться полностью доказанной, во-первых, замечательным опытом Физо и, во-вторых, нашим собственным исследованием. Экспериментальная проверка первой гипотезы составляет цель настоящей работы.

Если бы Земля была прозрачным телом, то, учитывая только что упомянутые эксперименты, вероятно, можно было бы допустить, что межмолекулярный эфир находится в пространстве в покое, несмотря на движение Земли по орбите; но мы не имеем права распространять выводы из этих экспериментов на непрозрачные тела. Однако вряд ли можно сомневаться, что эфир может проходить и действительно проходит через металлы. Лоренц приводит в качестве иллюстрации трубку ртутного манометра. Когда трубка наклонена, эфир, находящийся в пространстве над ртутью, безусловно, выталкивается оттуда, поскольку он несжимаем. (Можно возразить, что он может выходить через пространство между ртутью и стенками; но это можно предотвратить путем амальгамирования стенок.) Но опять-таки мы не имеем права предположить, что он выходит совершенно свободно, и если бы существовало какое-то сопротивление, хотя и слабое, мы не могли бы, конечно, полагать, что непрозрачное тело, такое, как Земля в целом, обеспечивает свободное прохождение эфира через всю эту массу. Но, как удачно отмечает Лоренц, «как бы то ни было, по моему мнению, в этом вопросе, также важном, лучше не позволять себе руководствоваться соображениями, основанными на правдоподобности или простоте той или иной гипотезы, а обращаться к опыту, чтобы научиться узнавать состояние покоя или движения, в котором находится эфир на поверхности Земли.

В апреле 1881 г. был предложен и испытан метод для решения этого вопроса.

При выводе формулы для измеряемой величины тогда было упущено из виду влияние движения Земли через эфир на путь луча, перпендикулярного этому движению. (Здесь можно отметить, что ошибка была указана автору последней работы А. Потье (Париж) зимой 1881 г.) Обсуждение этого упущения и всего эксперимента составляет предмет очень глубокого анализа Г.А. Лоренца, который выяснил, что данным эффектом ни в коем случае нельзя пренебрегать. Как следствие, в действительности величина, которая должна быть измерена, составляет только половину предполагавшейся величины, и, поскольку последняя уже была едва за пределами ошибок эксперимента, выводы, сделанные из результатов опыта, могли вполне основательно подвергаться сомнению. Однако, поскольку основная часть теории сомнению не подлежит, было решено повторить эксперимент с такими изменениями, которые давали бы уверенность в том, что теоретический результат достаточно велик, чтобы не быть скрытым экспериментальными погрешностями. Теория метода может быть кратко изложена следующим образом.

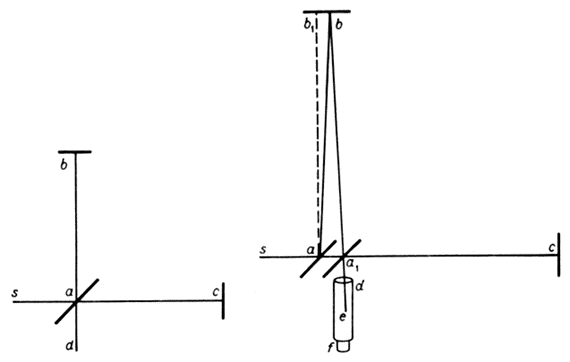
Рис. 1. Схема интерферометра Майкельсона

Пусть sa (рис. 1а) – луч света, который частично отражается по аb, а частично проходит по ас и возвращается зеркалами и c по ba и ca. Луч ba частично пропускается по ad, и са частично отражается по ad. Тогда, если пути аb и ас равны, два луча интерферируют вдоль ad. Предположим теперь, что эфир находится в покое, а весь прибор движется в направлении sc со скоростью движения Земли по орбите. Направления и расстояния, проходимые лучами, изменяются так. Луч sa отражается по аb (рис. 1б), причем угол bab₁ равен углу аберрации α, возвращается по ba₁ (aba₁ = 2α) θ попадает в фокус зрительной трубы, направление которой не меняется. Пропущенный луч идет по ас, возвращается по са и отражается в а₁, образуя угол са₁е. равный 90° – α, и поэтому все-таки совпадает с первым лучом. Можно отметить, что теперь лучи ba₁ и са₁ не встречаются в точности в одной и той же точке а₁, хотя разность составляет величину второго порядка малости; это не влияет на справедливость рассуждений. Пусть теперь требуется найти разность двух путей света аbа₁ и аса₁.

Пусть V – скорость света; v – скорость движения Земли по орбите; D – расстояние аb или ас; Т – время, которое требуется свету для прохождения от а до с, Т₁ – время, необходимое свету для возвращения от c к а₁ (рис. 1а).

Тогда Т = D / (V – v), Т₁ = D / (V + v).

Полное время движения туда и обратно равно

T + T₁ = 2D · V / (V₂ – v₂),

и расстояние, пройденное за это время, равно

2D · V₂ / (V₂ – v₂) ≈ 2D · (1 + v₂/V₂),

если пренебречь членами четвертого порядка.

Длина другого пути, очевидно, равна

или с той же точностью 2D · (1 + v₂ / V₂).

Поэтому разность равна D · v₂/V₂. Если теперь повернуть весь прибор на 90°, то разность будет наблюдаться в противоположном направлении; следовательно, смещение интерференционных полос должно быть 2D · v₂/V₂. Учитывая только орбитальное движение Земли, это должно быть равно 2D ·10^–8. Если, как было в первом эксперименте, D = 2·10⁶ длин волн желтого света, то ожидаемое смещение должно составлять 0,04 расстояния между интерференционными полосами. В первом эксперименте одна из основных встретившихся трудностей состояла в приведении прибора во вращение без создания искажений, другая же – его крайняя чувствительность к вибрациям. Она была столь велика, что при работе в городе, даже в два часа ночи, невозможно было наблюдать интерференционные полосы, кроме как в течение коротких промежутков времени. В итоге, как уже отмечалось, величина, которая должна была наблюдаться, а именно смещение, несколько меньшее, чем одна двадцатая часть расстояния между интерференционными полосами, могла быть слишком малой, чтобы быть зарегистрированной, когда она маскируется погрешностями эксперимента.

Первая из названных трудностей была полностью устранена путем установки прибора на массивный камень, плавающий в ртути; вторая же была преодолена посредством увеличения пути света вследствие повторных отражений до величины, почти в десять раз превосходившей первоначальную.

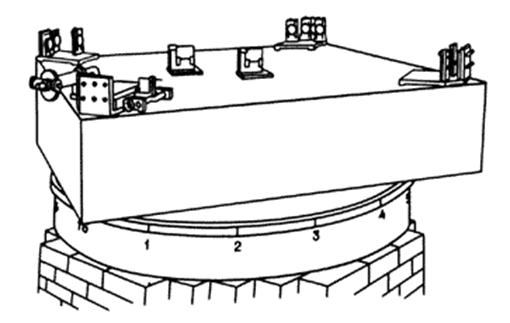
Рис. 2. Внешний вид интерферометра

Вид прибора показан на рис. 2, его вертикальное сечение – на рис. 3, а ход лучей в нем – на рис. 4. Камень а (рис. 4) имел площадь около 1,5 х 1,5 м и толщину 0,3 м. Он покоился на кольцеобразном деревянном поплавке с внешним диаметром 1,5 м, внутренним диаметром 0,7 м и толщиной 0,25 м. Поплавок располагался на ртути, содержавшейся в чугунном лотке cc толщиной 1,5 см и таких размеров, что вокруг поплавка в нем оставалось свободное пространство около сантиметра.

Рис. 3. Разрез опоры интерферометра

Шпилька d, направляемая рычагами gggg, совпадает с гнездом е, проделанным в поплавке. Посредством ручки, надетой в f, она может либо вставляться в гнездо, либо выниматься из него. Эта шпилька делает поплавок соосным с лотком, но не несет ни малейшей части веса камня. Кольцеобразный чугунный лоток опирается на цементную подложку, лежащую на низком кирпичном основании, выложенном в форме полого восьмиугольника.

В каждом углу камня помещалось по четыре зеркала ddee (рис. 3). Вблизи центра камня находилась плоскопараллельная стеклянная пластинка . Все это было расположено так, что свет от горелки Аргана⁵ а, проходя через линзу, падал на таким образом, чтобы частично отражаться к d₁. Два пучка, показанные на рисунке, проходили пути bdedbf и bd₁e₁d₁bf соответственно и наблюдались в зрительную трубу f. И труба f, и горелка а вращались вместе с камнем. Зеркала были сделаны из зеркальной бронзы и тщательно обработаны до получения оптически плоских поверхностей 5 см в диаметре: стекла и с были плоскопараллельными, одинаковой толщины 1,25 см; их поверхности имели размеры 5,0 х 7,5 см. Второе стекло ставилось на пути одного из пучков, чтобы скомпенсировать прохождение второго пучка через стекло той же толщины. Вся оптическая часть прибора содержалась под деревянным кожухом для предотвращения воздушных потоков и быстрых изменений температуры.

Рис. 4. Ход лучей в интерферометре

Настройка проводилась так. С помощью винтов в отливках, удерживавших зеркала, к которым последние прижимались пружинами, зеркала устанавливались так, чтобы свет обоих пучков мог быть виден в зрительную трубу. Посредством легкого деревянного стержня, достававшего по диагонали от зеркала до зеркала, измерялись длины двух путей, причем расстояния отсчитывались по маленькой стальной шкале с точностью до десятых долей миллиметра. Затем разность длин двух путей ликвидировалась путем передвижения зеркала е₁. Это зеркало имело три регулировки; имелись регулировки по высоте и азимуту, как и у других зеркал, но только более тонкие, а также регулировка в направлении падающего пучка, благодаря ему оно скользило взад и вперед, оставаясь, однако, с высокой точностью параллельным своей начальной плоскости. Все три регулировки могли производиться при закрытом деревянном кожухе.

Поскольку теперь пути были приближенно равны, два изображения источника света или какого-либо другого хорошо очерченного предмета сводились вместе и зрительная труба оказывалась настроенной на отчетливое наблюдение ожидаемых интерференционных полос. Когда они появлялись, белый свет заменялся на свет натрия. Путем регулировки зеркала е₁ полосы делались настолько отчетливыми, насколько это было возможно; затем возвращался белый свет, а винт, меняющий длину пути, приводился в очень медленное вращение (один оборот винта с сотней шагов резьбы на один дюйм менял путь примерно на 1000 длин волны) до тех пор, пока окрашенные интерференционные полосы не покажутся вновь в белом свете. Это давало удобную ширину и положение полос, и теперь прибор был готов для наблюдений.

Наблюдения проводились следующим образом. Вокруг чугунного лотка имелось шестнадцать эквидистантных отметок. Прибор приводился в очень медленное вращение (один оборот за шесть минут), и через несколько минут в момент прохождения одной из отметок пересечение нитей микрометра наводилось на самую яркую интерференционную полосу. Вращение происходило столь медленно, что это можно было сделать легко и точно. Отмечалось показание головки винта микрометра и делался очень легкий и плавный толчок для поддержания движения камня. При прохождении следующей отметки процедура повторялась, и все это продолжалось до тех пор, пока прибор не завершал шесть оборотов. Было обнаружено, что при поддержании прибора в состоянии медленного равномерного движения результаты оказывались гораздо более однородными и согласующимися между собой, чем когда камень останавливался для каждого наблюдения, поскольку эффекты деформаций могли быть заметными по крайней мере в течение полуминуты после того, как камень остановился, а за это время вступали в действие эффекты изменения температуры.