Дифференциальные уравнения движения точки. Решение задач динамики точки

Министерство Общего и профессионального технического образования

Московский Государственный Технический Университет МАМИ

Кафедра: Теоретическая механика

Реферат на тему:

Дифференциальные уравнения движения точки.

Решение задач динамики точки.

Студент: Зиновьев М.Ю.

Группа: 3-АиУ-1

Преподаватель:

Эйнштейн (1879-1955)

Ньютон (1643-1727)

Галилей (1564-1642)

Аристотель (384-322 до н.э.)

Введение в динамику. Законы динамики.

Основные понятия и определения.

Динамикой называется раздел механики, в котором изучается движение материальных тел под действием сил.

Движение с чисто геометрической точки зрения рассматривается в кинематике. Отличие динамики состоит в том, что при изучении движения тел принимают во внимание как действующие на них силы, так и инертность самих материальных тел.

Понятие о силе, как об основной мере механического действия, оказываемого на материальное тело, было введено в статике. Но статика не касается вопроса о возможных изменениях действующих сил с течением времени., а при решении задач считали все силы постоянными. Между тем на движущееся тело наряду с постоянными силами действуют обычно силы переменные, модули и направления которых при движении тела изменяются. При этом переменными могут быть и заданные (активные) силы (Активной обычно называют силу, которая, начав действовать на покоящееся тело, может привести его в движение) и реакции связей.

Как показывает опыт, переменные силы могут определенным образом зависеть от времени, положения тела и его скорости. В частности, от времени зависит сила тяги электровоза при постепенном выключении или включении реостата или сила, вызывающая колебания фундамента при работе мотора с плохо центрированным валом; от положения тела зависит Ньютонова сила тяготения или сила упругости пружины; от скорости зависят силы сопротивления среды. В заключение отметим, что все введенные в статике понятия и полученные там результаты относятся в равной мере и к переменным силам, так как условие постоянства сил нигде в статике не использовалось.

Инертность тела проявляется в том, что оно сохраняет свое движение при отсутствии действующих сил, а когда на него начинает действовать сила, то скорости точек тела изменяются не мгновенно, а постепенно и тем медленнее, чем больше инертность этого тела. Количественной мерой инертности материального тела является физическая величина, называемая массой тела (Масса является еще мерой гравитационных свойств тела), В классической механике масса т рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.

Кроме суммарной массы движение тела зависит еще в общем случае от формы тела, точнее от взаимного расположения образующих его частиц, т.е. от распределения масс в теле.

Чтобы при первоначальном изучении динамики отвлечься от учета формы тела (распределения масс), вводят абстрактное понятие о материальной точке, как о точке, обладающей массой, и начинают изучение динамики с динамики материальной точки.

Из кинематики известно, что движение тела слагается в общем случае из поступательного и вращательного. При решении конкретных задач материальное тело можно рассматривать как материальную точку в тех случаях, когда по условиям задачи допустимо не принимать во внимание вращательную часть движения тела. Например, материальной точкой можно считать планету при изучении ее движения вокруг Солнца или артиллерийский снаряд при определении дальности его полета и т.п. Соответственно поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе всего тела.

Изучать динамику обычно начинают с динамики материальной точки, так как естественно, что изучение движения одной точки должно предшествовать изучению движения системы точек и, в частности, твердого тела.

ЗАКОНЫ ДИНАМИКИ.

ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ

В основе динамики лежат законы, установленные путем обобщения результатов целого ряда опытов и наблюдений, посвященных изучению движения тел, и проверенные обширной общественно-производственной практикой человечества. Систематически законы динамики были впервые изложены И. Ньютоном в его классическом сочинении «Математические начала натуральной философии», изданном в 1687г. (Есть прекрасный русский перевод, сделанный А. Н. Крымовым. См.: Собрание трудов акад. А. Н. Крылова, т. VII. М.— Л., 1936). Сформулировать эти законы можно следующим образом.

Первый закон (закон инерции):

изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние. Движение, совершаемое точкой при отсутствии сил, называется движением по инерции.

Закон инерции отражает одно из основных свойств материи — пребывать неизменно в движении. Важно отметить, что развитие динамики как науки стало возможным лишь после того, как Галилеем был открыт этот закон (1638 г.) и тем самым опровергнута господствовавшая со времен Аристотеля точка зрения о том, что движение тела может происходить только под действием силы.

Существенным является вопрос о том, по отношению к какой системе отсчета справедлив закон инерции. Ньютон предполагал, что существует некое неподвижное (абсолютное) пространство, по отношению к которому этот закон выполняется. Но по современным воззрениям пространство — это форма существования материи, и какого-то абсолютного пространства, свойства которого не зависят от движущейся в нем материи, не существует. Между тем, поскольку закон имеет опытное происхождение (еще Галилей указал, что к этому закону можно прийти, рассматривая движение шарика по наклонной плоскости со все убывающим углом наклона), должны существовать системы отсчета, в которых с той или иной степенью приближения данный закон будет выполняться. В связи с этим в механике, переходя, как обычно, к научной абстракции, вводят понятие о системе отсчета, в которой справедлив закон инерции, постулируют ее существование и называют инерциальной системой отсчета.

Можно ли данную реальную систему отсчета при решении тех или иных задач механики рассматривать как инерциальную, устанавливается путем проверки того, в какой мере результаты, полученные в предположении, что эта система является инерциальной, подтверждаются опытом. По данным опыта для нашей Солнечной системы инерциальной с высокой степенью точности можно считать систему отсчета, начало которой находится в центре Солнца, а оси направлены на так называемые неподвижные звезды. При решении большинства технических задач инерциальной, с достаточной для практики точностью, можно считать систему отсчета, жестко связанную с Землей.

Второй закон (основной закон динамики)

устанавливает, как изменяется скорость точки при действии на нее какой-нибудь силы, а именно: произведение массы материальной точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы.

Математически этот закон выражается векторным равенством

(1)

При этом между модулями ускорения и силы имеет место зависимость

та=F . (1')

Второй закон динамики, как и первый, имеет место только по отношению к инерциальной системе отсчета. Из этого закона непосредственно видно, что мерой инертности материальной точки является ее масса, поскольку при действии данной силы точка, масса которой больше, т. е. более инертная, получит меньшее ускорение и наоборот.

Если на точку действует одновременно несколько сил, то они, как это следует из закона параллелограмма сил, будут эквивалентны одной силе, т. е. равнодействующей , равной геометрической сумме данных сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид

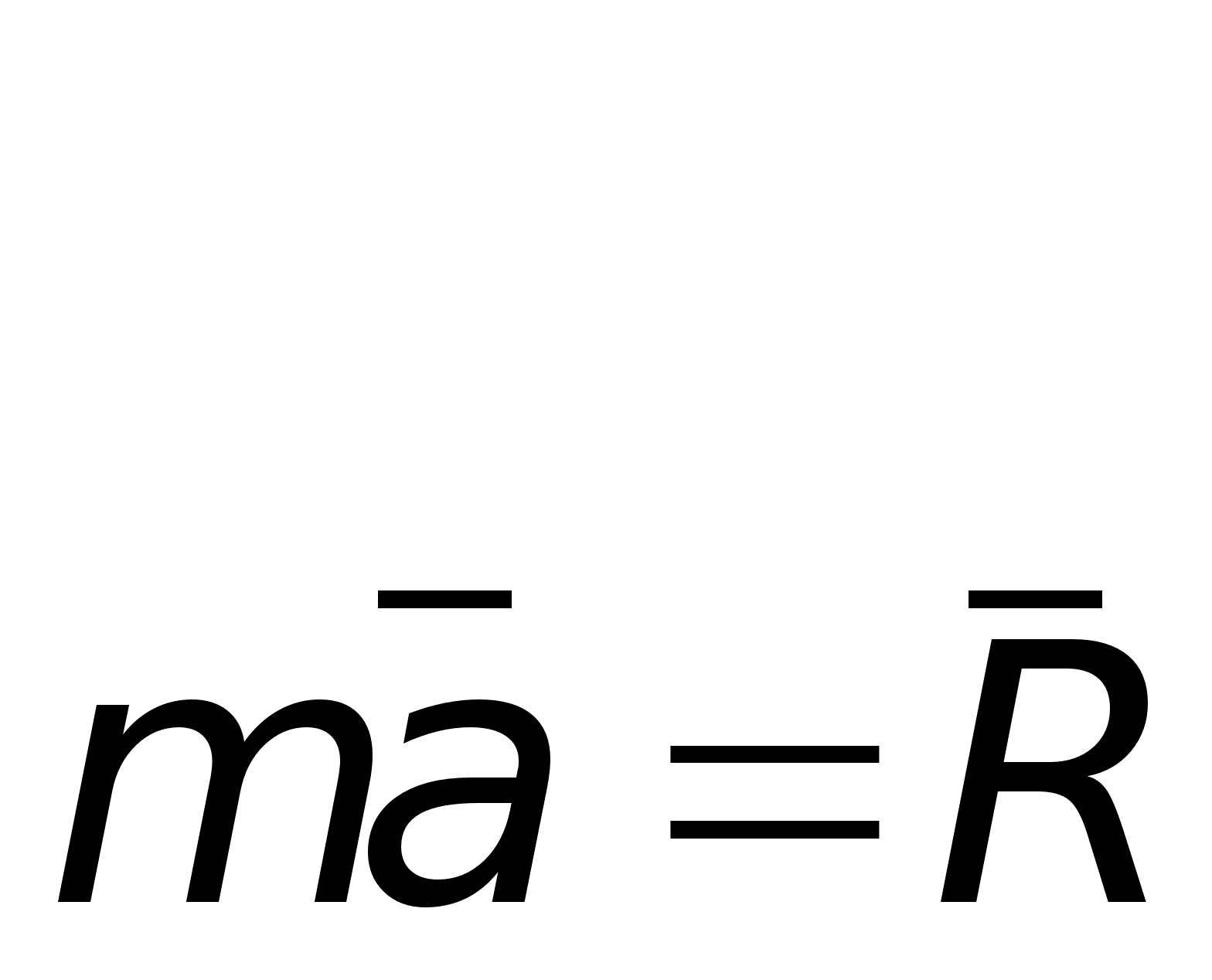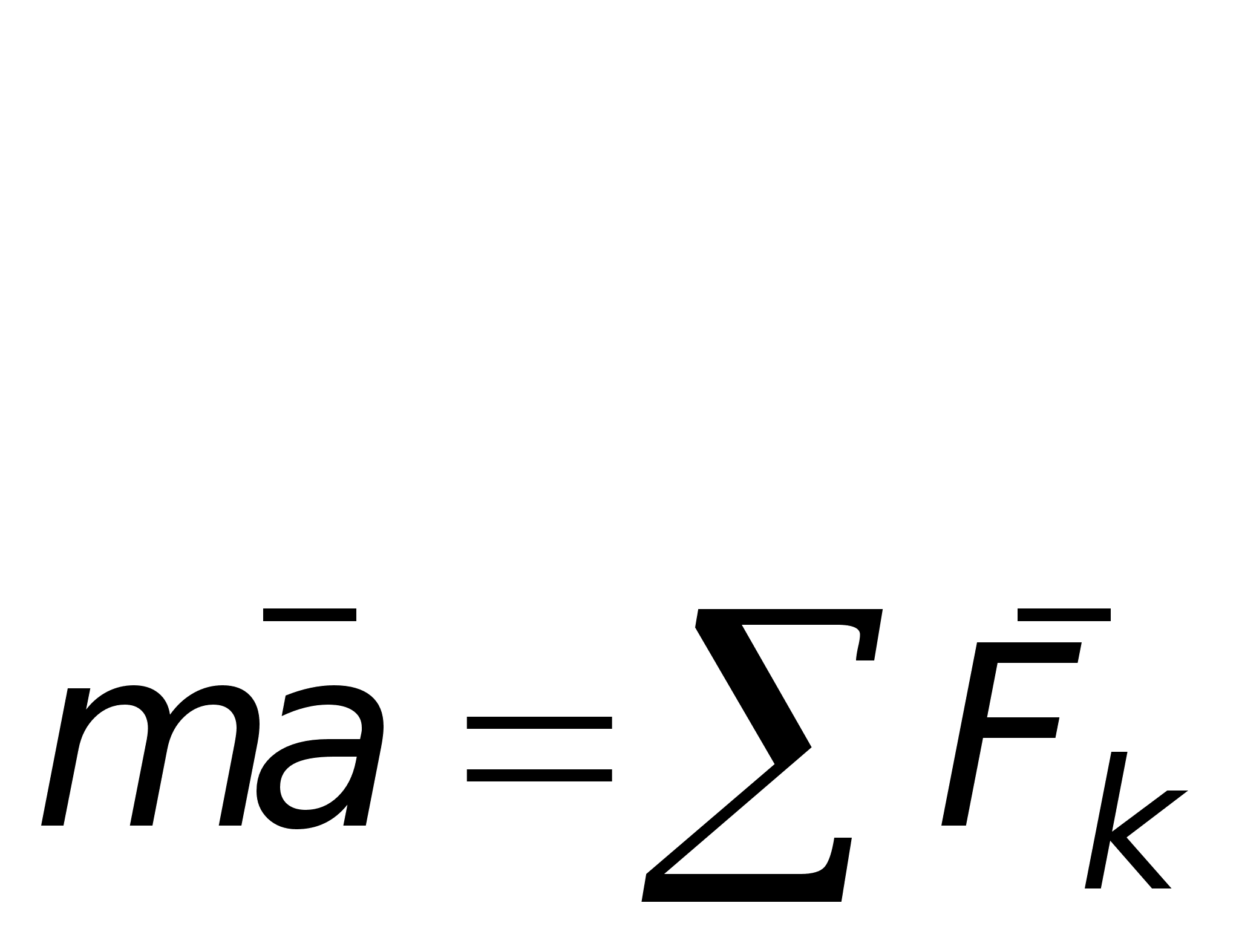или (2)

Этот же результат можно получить, используя вместо закона параллелограмма закон независимости действия сил, согласно которому при одновременном действии на точку нескольких сил каждая из них сообщает точке такое же ускорение, какое она сообщила бы, действуя одна.

Третий закон (закон равенства действия и противодействия) устанавливает характер механического взаимодействия между материальными телами. Для двух материальных точек он гласит:

две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.

Этим законом пользуются в статике. Он играет большую роль в динамике системы материальных точек, как устанавливающий зависимость между действующими на эти точки внутренними силами.

При взаимодействии двух свободных материальных точек, они, согласно третьему и второму законам динамики, будут двигаться с ускорениями, обратно пропорциональными их массам.

Задачи динамики. Для свободной материальной точки задачами динамики являются следующие:

зная закон движения точки, определить действующую на нее силу (первая задача динамики);
2) зная действующие на точку силы, определить закон движения точки (вторая, или основная, задача динамики).

Для несвободной материальной точки, т. е. точки, на которую наложена связь, вынуждающая ее двигаться по заданной поверхности или кривой, первая задача динамики обычно состоит в том, чтобы, зная движение точки и действующие на нее активные силы, определить реакцию связи. Вторая (основная) задача динамики при несвободном движении распадается на две и состоит в том, чтобы, зная действующие на точку активные силы, определить: а) закон движения точки, б) реакцию наложенной связи.

СИСТЕМЫ ЕДИНИЦ

Для измерения всех механических величин оказывается достаточным ввести независимые друг от друга единицы измерения каких-нибудь трех величин. Двумя из них принято считать единицы длины и времени. В качестве третьей оказывается наиболее удобным выбрать единицу измерения или массы, или силы. Так как эти величины связаны равенством (1), то произвольно единицу измерения каждой из них выбрать нельзя. Отсюда вытекает возможность введения в механике двух принципиально отличных друг от друга систем единиц.

Первый тип систем единиц.

В этих системах за основные принимаются единицы длины, времени и массы, а сила измеряется производной единицей.

К таким системам относится Международная система единиц измерения физических величин (СИ), в которой основными единицами измерения механических величин являются метр (м), килограмм массы (кг) и секунда (с). Единицей же измерения силы является производная единица — 1 ньютон (Н);

1 Н — это сила, сообщающая массе в 1 кг ускорение 1 м/с² (1Н==1 кг-м/с²). О том, что собой представляют 1 м, 1 кг и 1 с, известно из курса физики. Международная система единиц (СИ) введена в России как предпочтительная с 1961 г

Второй тип систем единиц.

В этих системах за основные принимаются единицы длины, времени и силы, а масса измеряется производной единицей.

К таким системам относится имевшая большое распространение в технике система МКГСС, в которой основными единицами являются метр (м), килограмм силы (кГ) и секунда (с). Единицей измерения массы в этой системе будет 1 кГс²^/м, т. е. масса, которой сила в 1 кГ сообщает ускорение 1 м/с².

Соотношение между единицами силы в системах СИ и МКГСС таково: 1 кГ=9,81 Н или 1 Н=0,102 кГ.

В заключение необходимо отметить, что надо различать понятия размерность величины и единица ее измерения. Размерность определяется только видом уравнения, выражающего значение данной величины, а единица измерения зависит еще от выбора основных единиц. Например, если, как это принято, обозначать размерность длины, времени и массы соответственно символами L, Т и М, то размерность скорости L/Т, а единицей измерения может быть 1 м/с, 1 км/ч и т. д.

ОСНОВНЫЕ ВИДЫ СИЛ

Рассмотрим следующие постоянные или переменные силы (законы изменения переменных сил, как правило, устанавливаются опытным путем).

Сила тяжести. Это постоянная сила , действующая на любое тело, находящееся вблизи земной поверхности. Модуль силы тяжести равен весу тела.

Опытом установлено, что под действием силы любое тело при свободном падении на Землю (с небольшой высоты и в безвоздушном пространстве) имеет одно и то же ускорение , называемое ускорением свободного падения, а иногда ускорением силы тяжести (Закон свободного падения тел был открыт Галилеем. Значение q в разных местах земной поверхности различно; оно зависит от географической широты места над уровнем моря. На широте Москвы (на уровне моря) q=9,8156м/с2

Тогда из уравнения (1') следует, что

Р=тq или т=Р/q . (3)

Эти равенства позволяют, зная массу тела, определить его вес (модуль действующей на него силы тяжести) или, зная вес тела, определить его массу. Вес тела или сила тяжести, как и величина q, изменяются с изменением широты и высоты над уровнем моря; масса же является для данного тела величиной неизменной.

Сила трения. Так будем кратко называть силу трения скольжения, действующую (при отсутствии жидкой смазки) на движущееся тело. Ее модуль определяется равенством

F=f*N (4)

где f — коэффициент трения, который будем считать постоянным;

N — нормальная реакция.

Сила тяготения. Это сила, с которой два материальных тела притягиваются друг к другу по закону всемирного тяготения, открытому Ньютоном. Сила тяготения зависит от расстояния и для двух материальных точек с массами и , находящихся на расстоянии r друг от друга, выражается равенством

где f—гравитационная постоянная (в СИ/=6,673*).

Сила упругости. Эта сила тоже зависит от расстояния. Ее значение можно определить исходя из закона Гука, согласно которому напряжение (сила, отнесенная к единице площади) пропорционально деформации. В частности, для силы упругости пружины получается значение

F=c (6)

где  — удлинение (или сжатие) пружины; с — так называемый коэффициент жесткости пружины (в СИ измеряется в Н/м).

Сила вязкого трения. Такая сила, зависящая от скорости, действует на тело при его медленном движении в очень вязкой среде (или при наличии жидкой смазки) и может быть выражена равенством

R=v (7)

где v — скорость тела; , — коэффициент сопротивления. Зависимость вида (7) можно получить исходя из закона вязкого трения, открытого Ньютоном.

Сила аэродинамического (гидродинамического) сопротивления. Эта сила тоже зависит от скорости и действует на тело, движущееся в такой, например, среде, как воздух или вода. Обычно ее величину выражают равенством

(8)

где р — плотность среды; S — площадь проекции тела на плоскость, перпендикулярную направлению движения (площадь миделя);

Сx:—безразмерный коэффициент сопротивления, определяемый обычно экспериментально и зависящий от формы тела и от того, как оно ориентировано при движении.

Инертная игравитационная массы.

Для экспериментального определения массы данного тела можно исходить из закона (1), куда масса входит как мера инертности и называется поэтому инертной массой. Но можно исходить и из закона (5), куда масса входит как мера гравитационных свойств тела и называется соответственно гравитационной (или тяжелой) массой. В принципе ни откуда не следует, что инертная и гравитационная массы представляют собой одну и ту же величину. Однако целым рядом экспериментов установлено, что значения обеих масс совпадают с очень высокой степенью точности (по опытам, проделанным советскими физиками (1971 г.),— с точностью до ). Этот экспериментально установленный факт называют принципом эквивалентности. Эйнштейн положил его в основу своей общей теории относительности (теории тяготения).

Исходя из изложенного, в механике пользуются единым термином «масса», определяя массу как меру инертности тела и его гравитационных свойств.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ. РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ

Для решения задач динамики точки будем пользоваться одной из следующих двух систем уравнений.

Уравнения в декартовых координатах.

Из кинематики известно, что движение точки в прямоугольных декартовых координатах задается уравнениями:

(9)

Задачи динамики точки состоят в том, чтобы, зная движение точки, т. е. уравнения (9), определить действующую на точку силу или, наоборот, зная действующие на точку силы, определить закон ее движения, т.е. уравнения (9). Следовательно, для решения задач динамики точки надо иметь уравнения, связывающие координаты х, у,zг этой точки и действующую на нее силу (или силы). Эти уравнения и дает второй закон динамики.

Рассмотрим материальную точку, движущуюся под действием сил 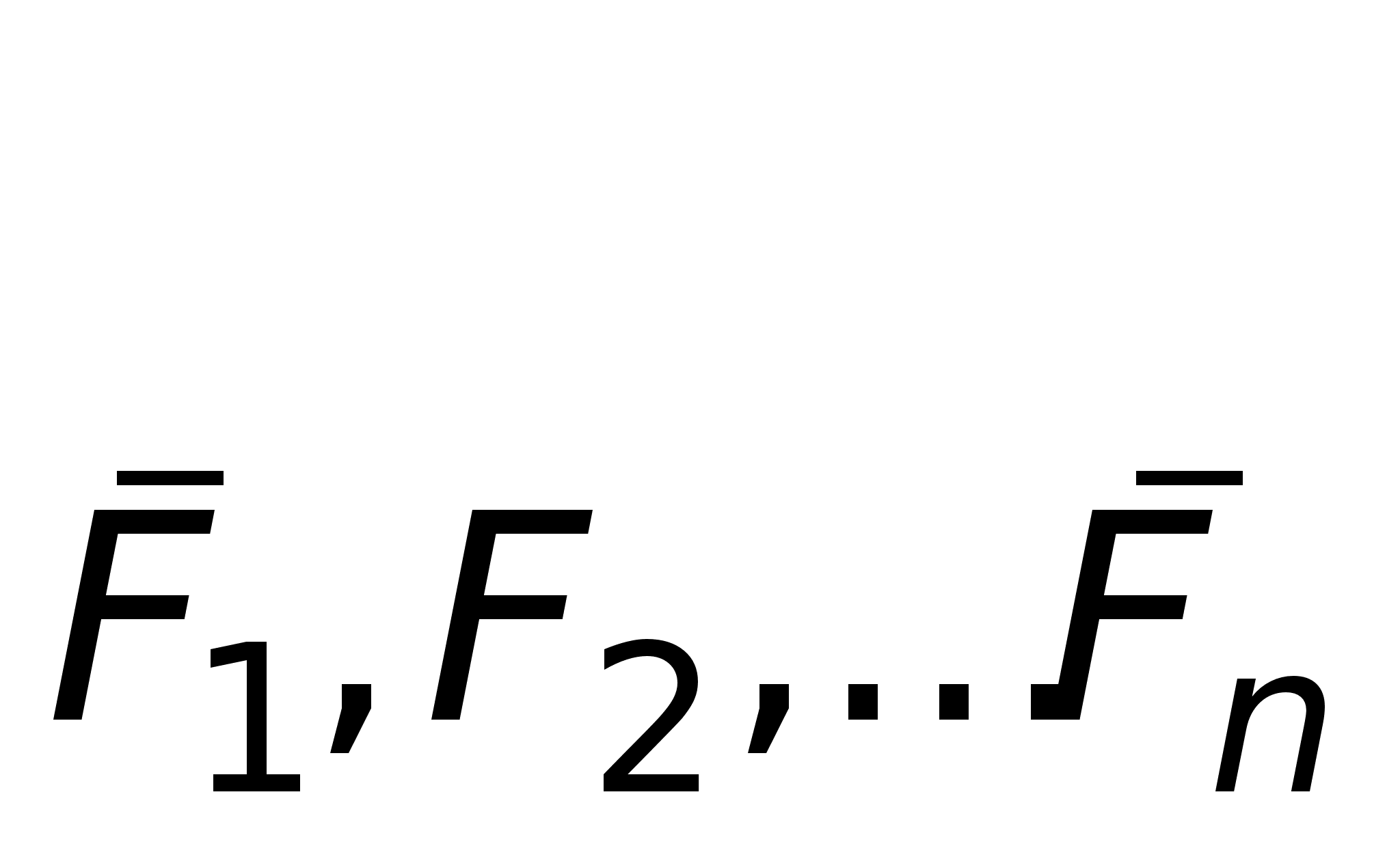., по отношению к инерциальной системе отсчета Охуг. Проектируя обе части равенства (2), т.е. равенства 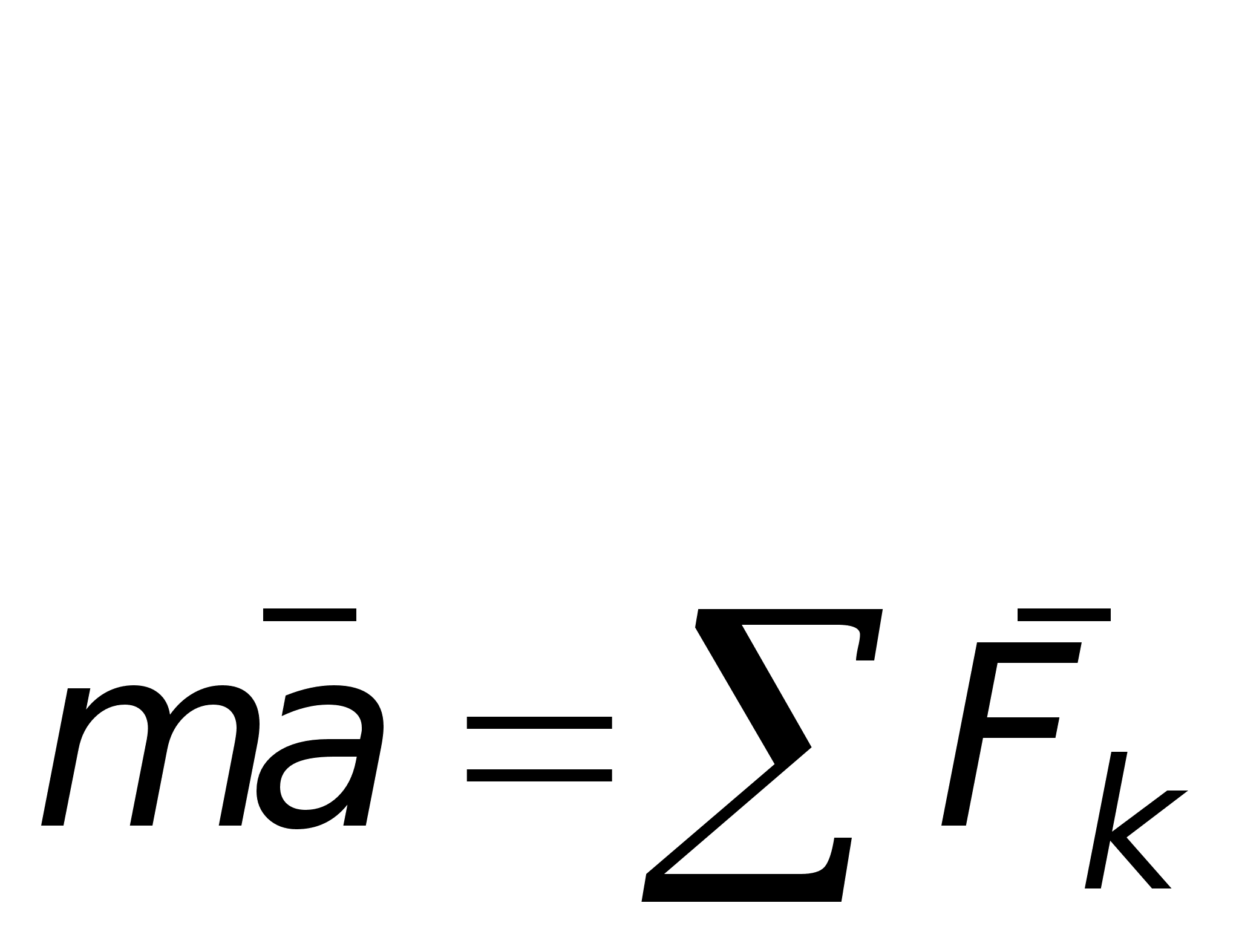оси х, у, zг и учитывая, что и т.д., получим

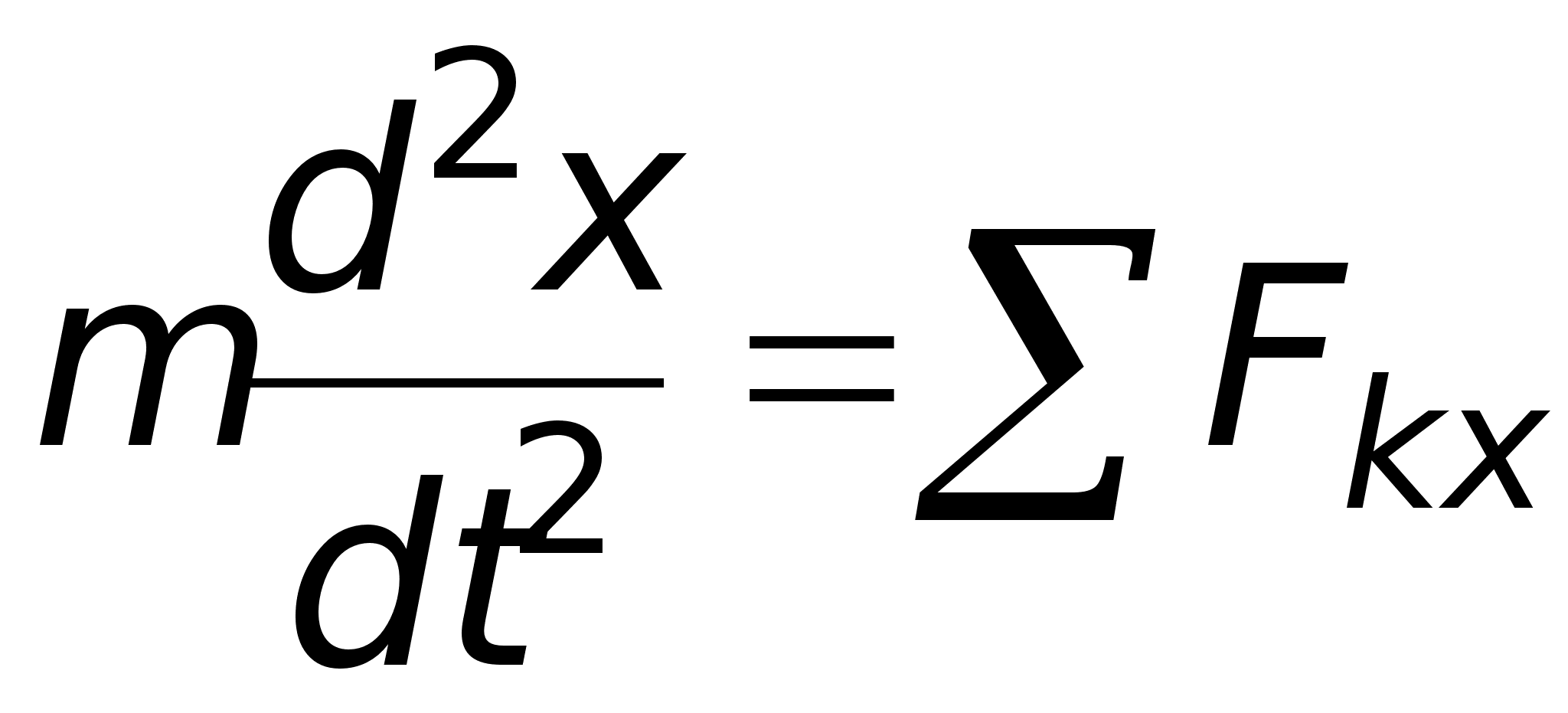
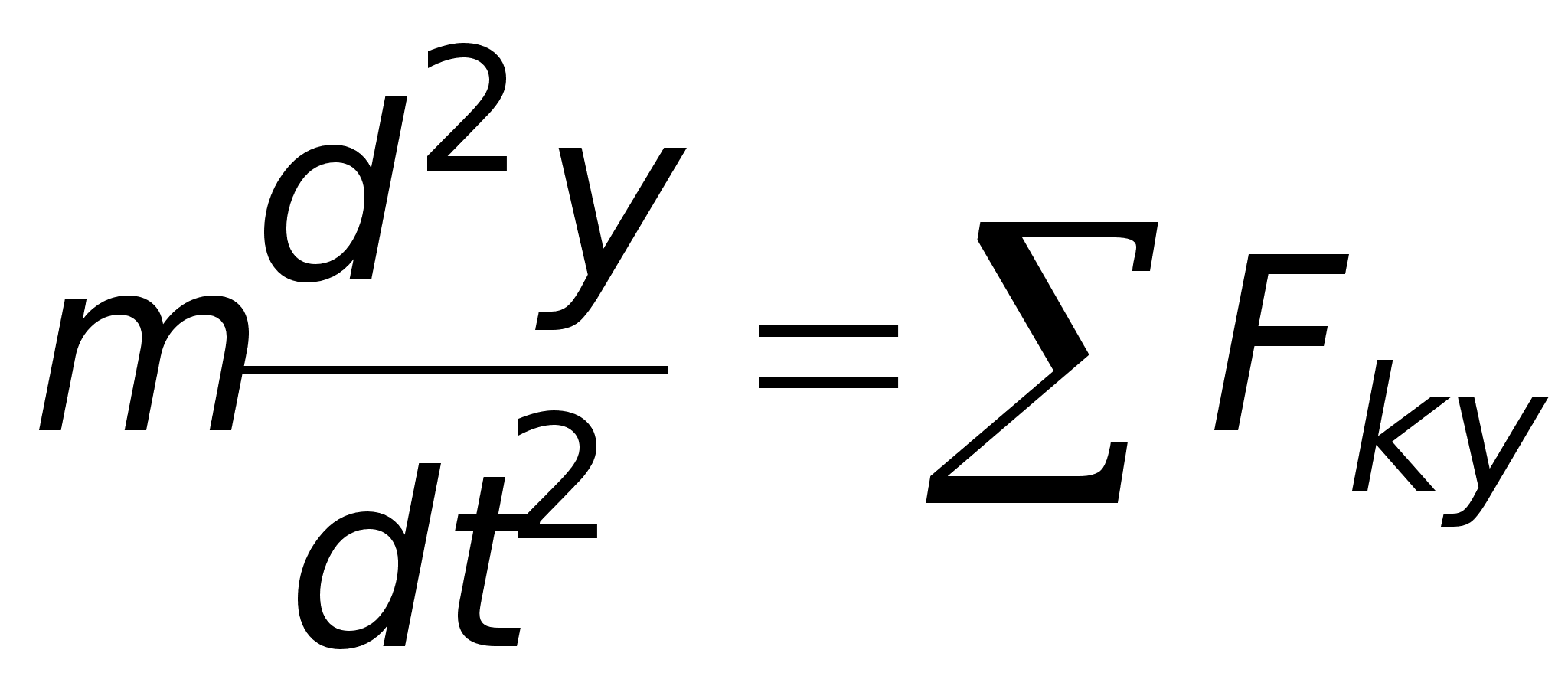
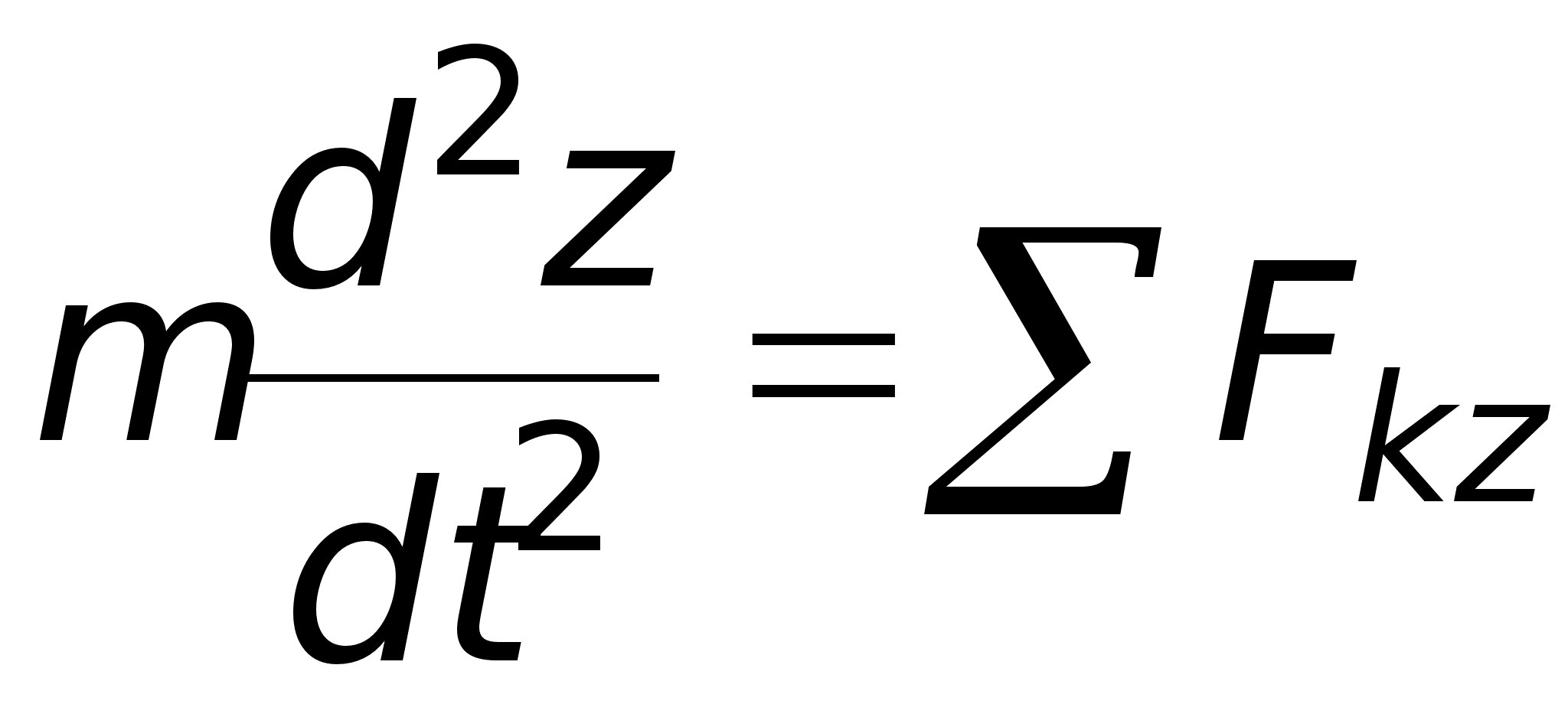(10)

или, обозначая вторые производные по времени двумя точками,

(10')

Это и будут искомые уравнения, т.е. дифференциальные уравнения движения точки в прямоугольных декартовых координатах. Так как действующие силы могут зависеть от времени t, от положения точки, т. е. от ее координат х, у,z, и от скорости, т. е. от , , то в общем случае правая часть каждого из уравнений (10) может быть функцией всех этих переменных, т. е. t, х, у, z,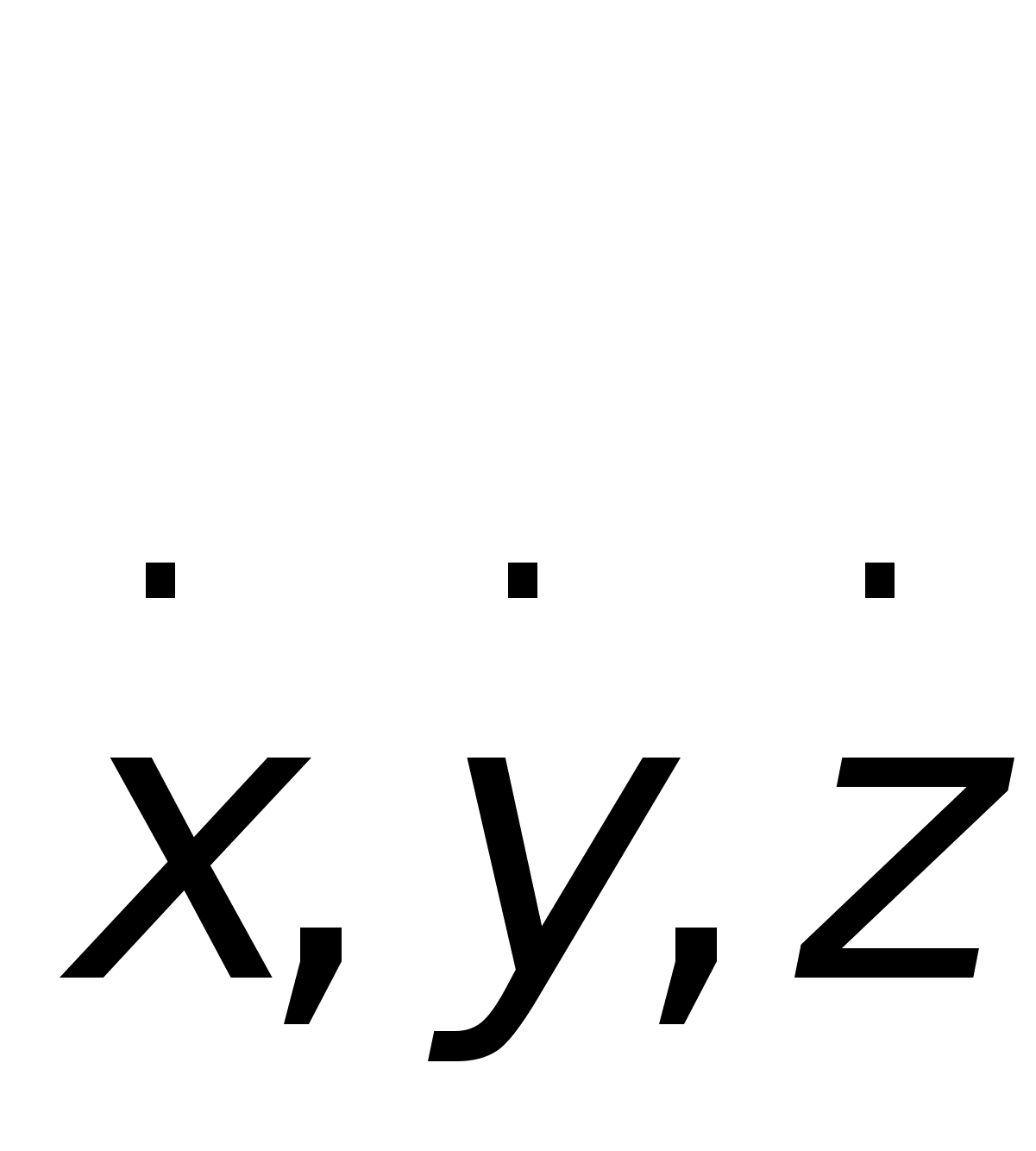одновременно.

Уравнения в проекциях на оси естественного трехгранника. Для получения этих уравнений спроектируем обе части равенства 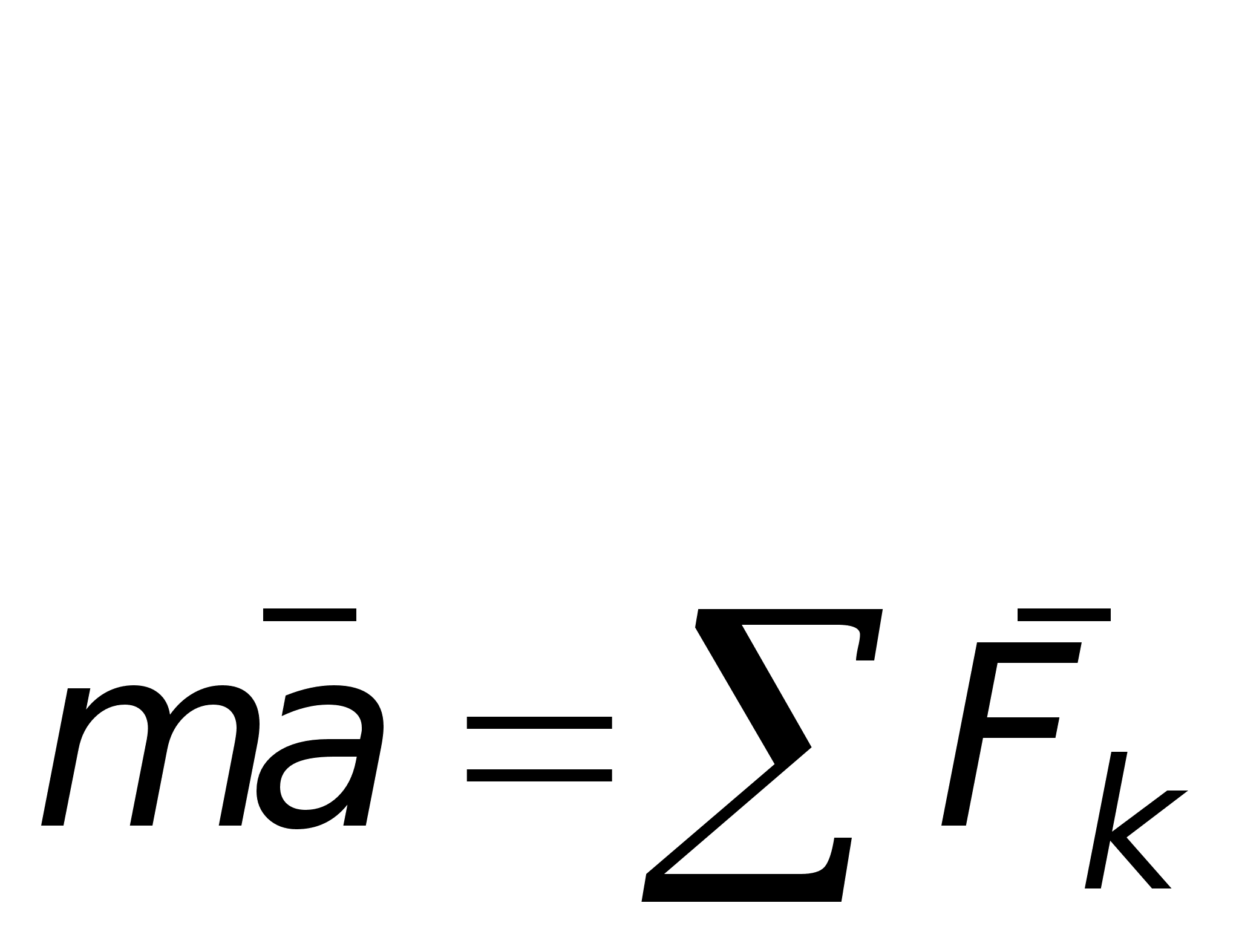на оси Mnb, т.е. на касательную М: к траектории точки, главную нормаль Мп, направленную в сторону вогнутости траектории, и бинормаль Mb



. Тогда, учитывая, что , , получим

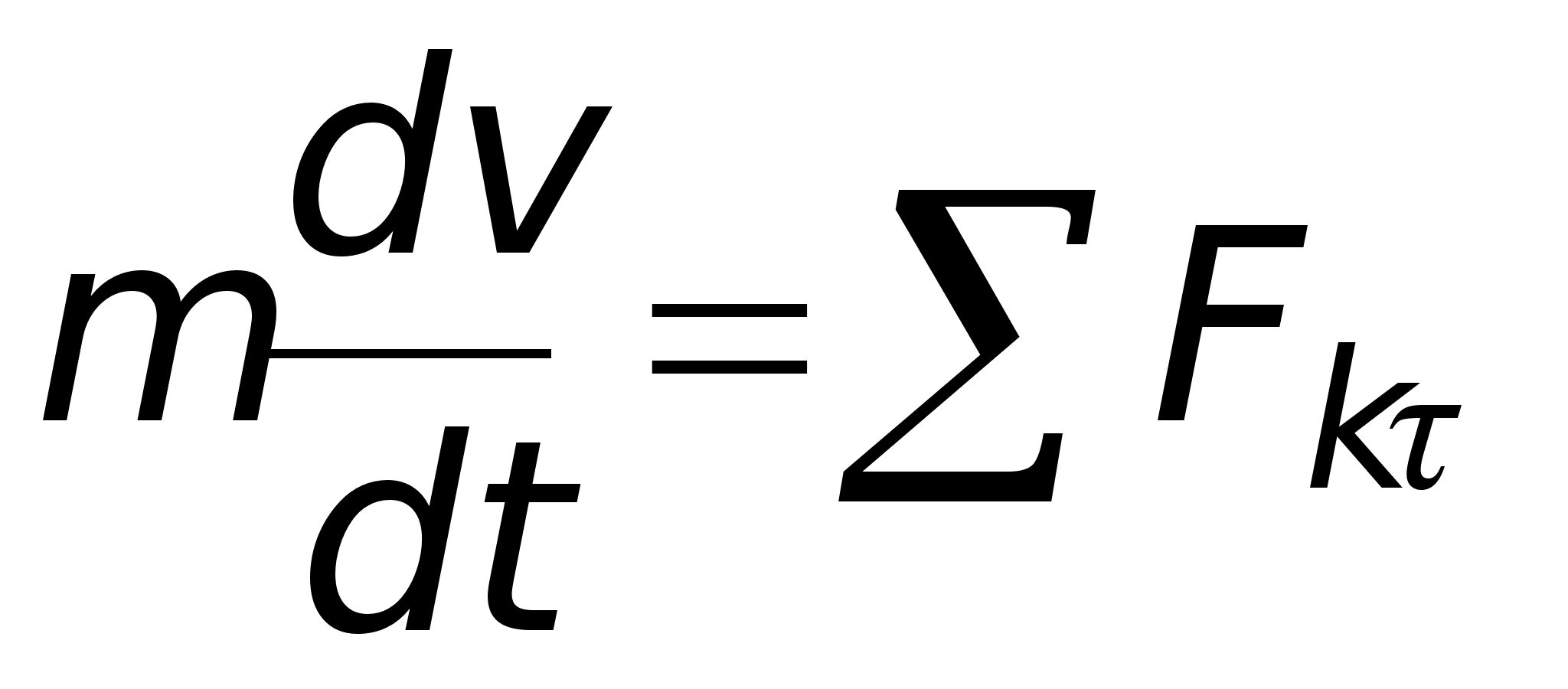
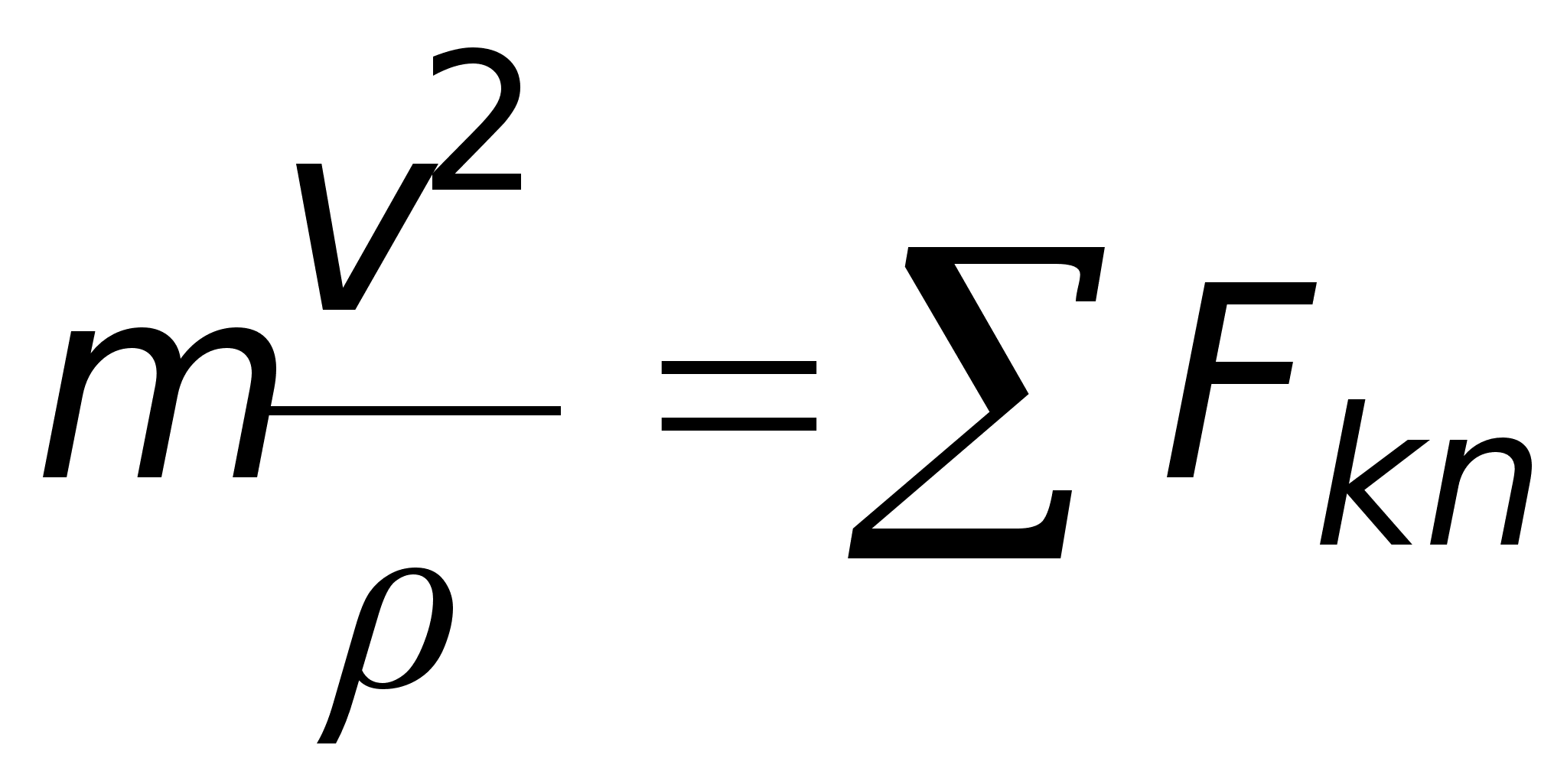
(11)

Уравнения (11), где v=ds!dt, представляют собой дифференциальные уравнения движения точки в проекциях на оси естественного трехгранника.

РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ

(ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ)

Если ускорение движущейся точки задано, то действующая сила или реакция связи сразу находится по уравнениям (1) или (2). При этом для вычисления реакции надо дополнительно знать активные силы. Когда ускорение непосредственно не задано, но известен закон движения точки, то для определения силы можно воспользоваться уравнениями (10) или (11).

РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ

Движение материальной точки будет прямолинейным, когда действующая на нее сила (или равнодействующая приложенных сил) имеет постоянное направление, а скорость точки в начальный момент времени равна нулю или направлена вдоль силы.

Если при прямолинейном движении направить вдоль траектории координатную ось Ох, то движение точки будет определяться первым из уравнений (10), т. е. уравнением

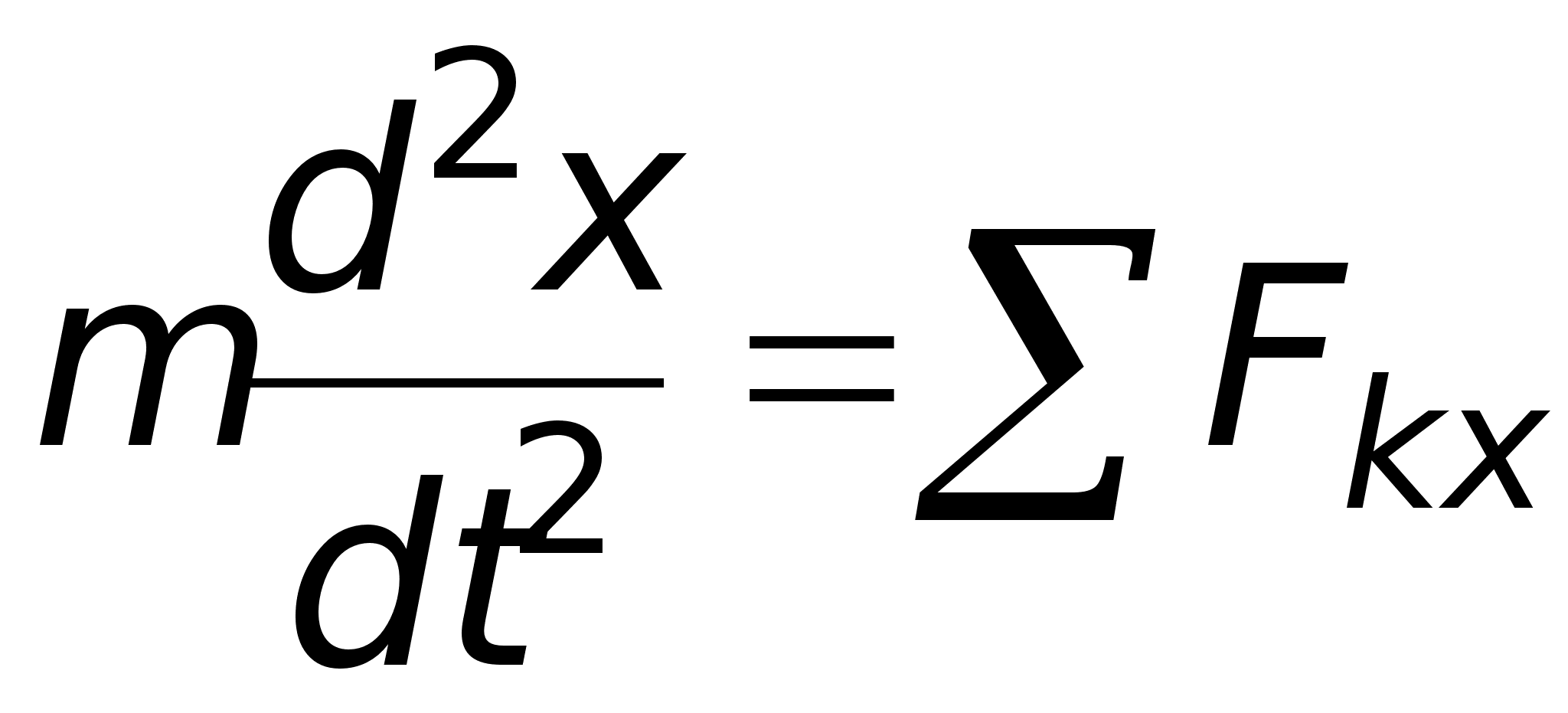или (12)

Уравнение (12) называют дифференциальным уравнением прямолинейного движения точки. Иногда его удобнее заменить двумя уравнениями, содержащими первые производные:

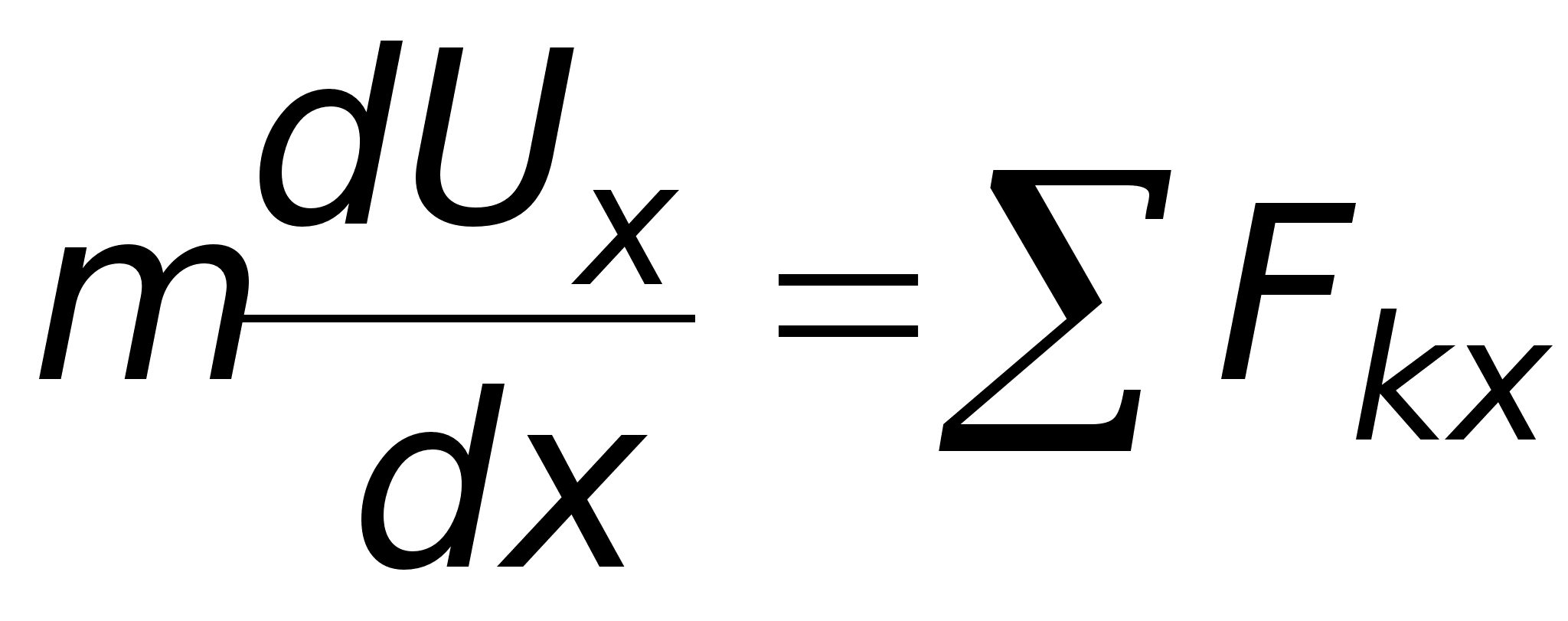
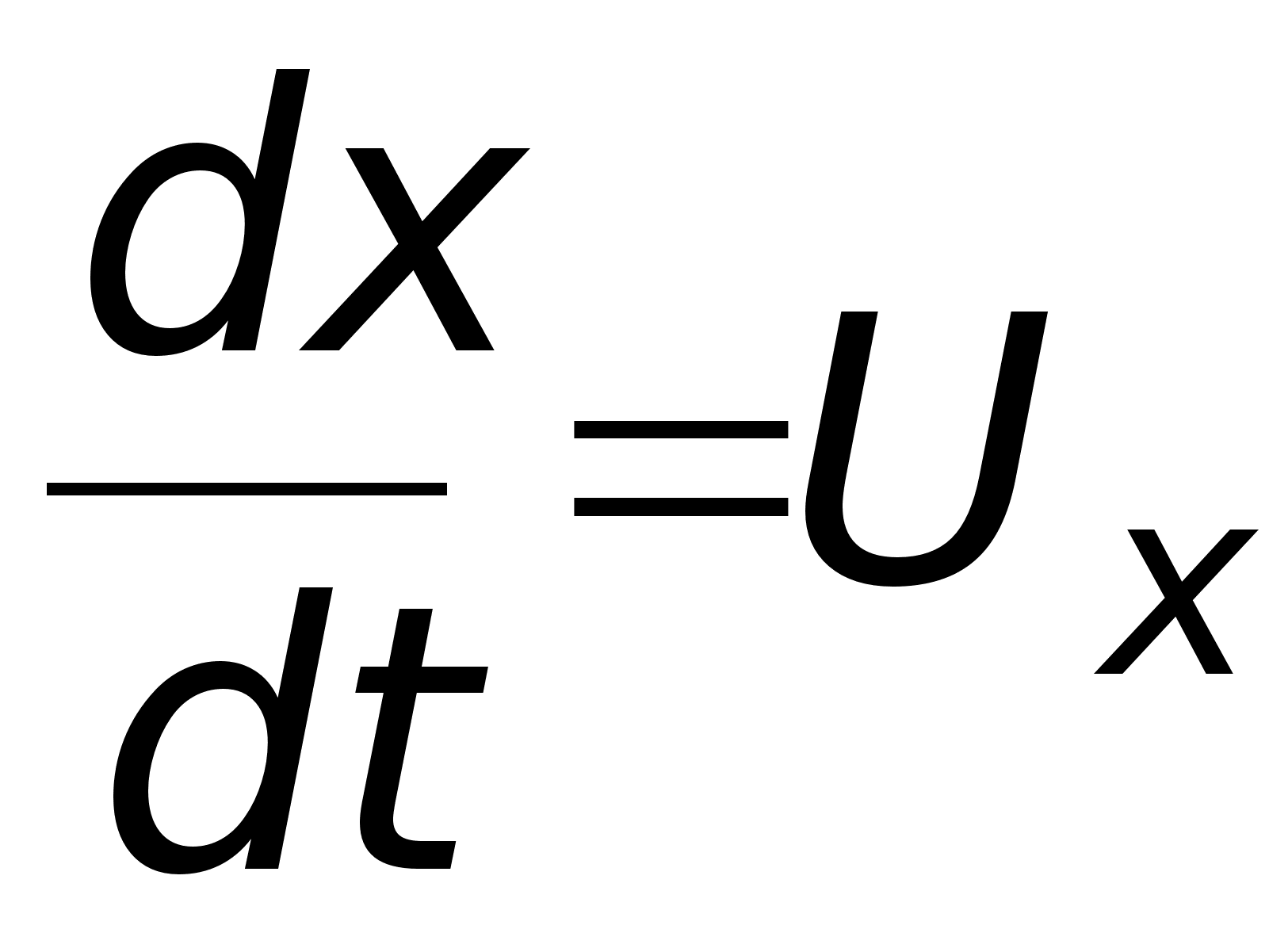(13)

В случаях, когда при решении задачи надо искать зависимость скорости от координаты х, а не от времени t (или когда сами силы зависят от х), уравнение (13) преобразуют к переменному х. Так какdVx/dt=dVx/dx*dx/dt=dVx/dx*Vx, то вместо (13) получим

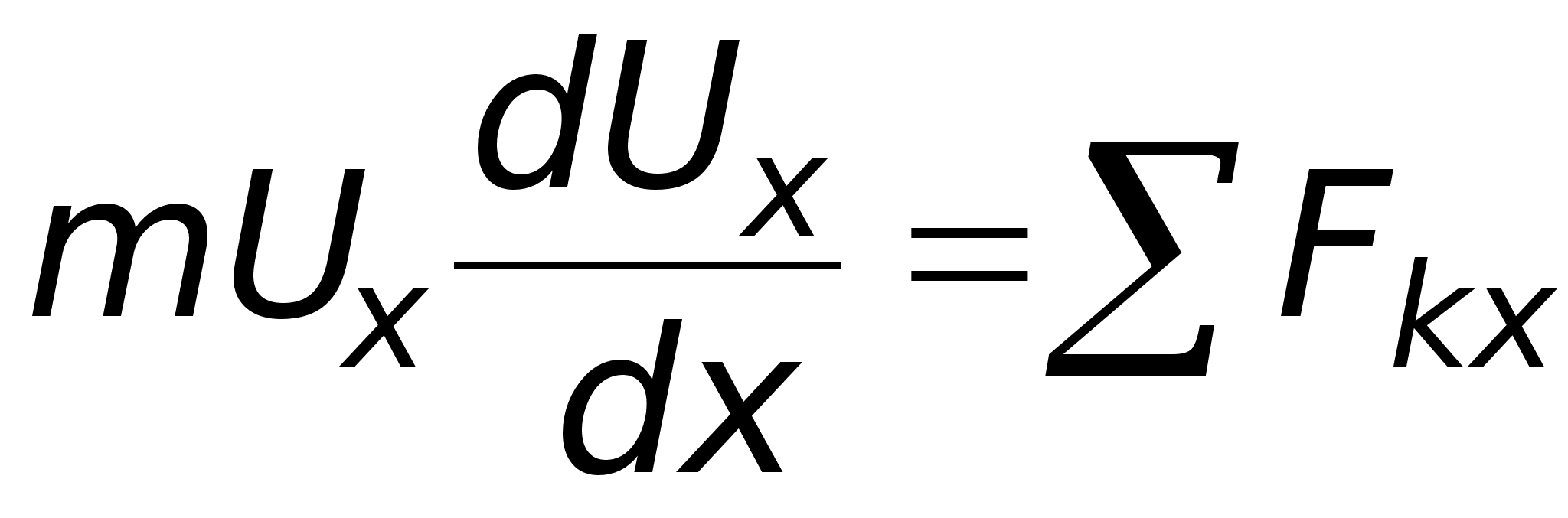
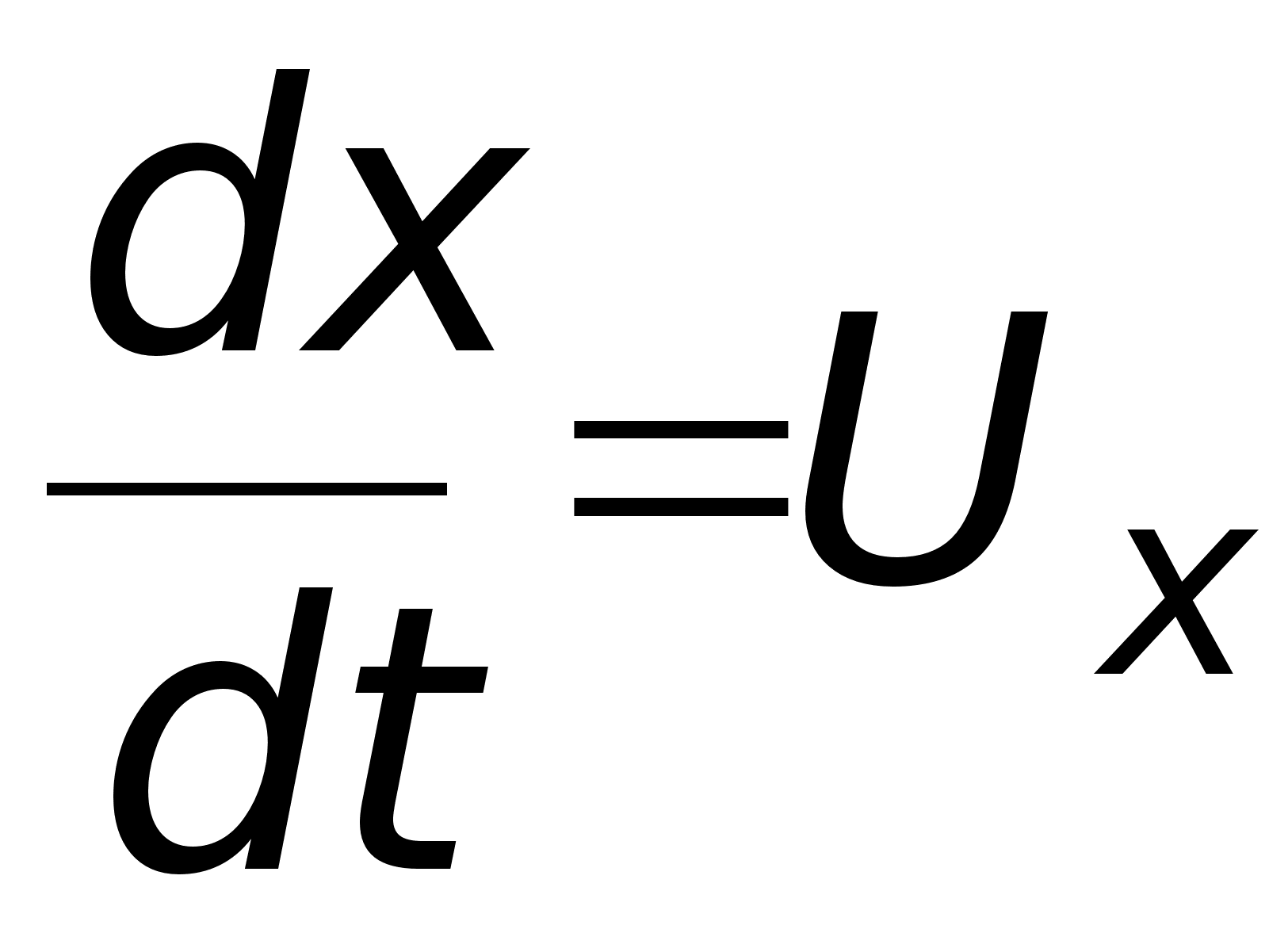(14)

Решение основной задачи динамики сводится к тому, чтобы из данных уравнений, зная силы, найти закон движения точки, т. е. x=f(t). Для этого надо проинтегрировать соответствующее дифференциальное уравнение. Чтобы яснее было, к чему сводится эта математическая задача, напомним, что входящие в правую часть уравнения (12) силы могут зависеть от времени t, от положения точки, т. е. от х, и от ее скорости, т. е. от Vy=x. Следовательно, в общем случае уравнение (12) с математической точки зрения представляет собой дифференциальное уравнение 2-го порядка, имеющее вид .

Если для данной конкретной задачи дифференциальное уравнение (12) будет проинтегрировано, то в полученное решение войдут две постоянные интегрирования и и общее решение уравнения (12) будет иметь вид

(15)

Чтобы довести решение каждой конкретной задачи до конца, надо определить значения постоянных . Для этого используются обычно так называемые начальные условия.

Изучение всякого движения будем начинать с некоторого определенного момента времени, называемого начальным моментом. От этого момента будем отсчитывать время движения, считая, что в начальный момент t=0. Обычно за начальный принимают момент начала движения под действием заданных сил. Положение, которое точка занимает в начальный момент, называется начальным положением, а ее скорость в этот момент — начальной скоростью (начальную скорость точка может иметь или потому, что до момента t=0 она двигалась по инерции, или в результате действия на нее до момента t=0 каких-то других сил). Чтобы решить основную задачу динамики, надо кроме действующих сил знать еще начальные условия, т. е. положение и скорость точки в начальный момент времени.

В случае прямолинейного движения начальные условия задаются в виде

При t=0 ,. (16)

По начальным условиям можно определить конкретные значения постоянных и найти частное решение уравнения (12), дающее закон движения точки, в виде

(17)