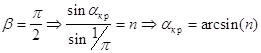Вывод и анализ формул Френеля на основе электромагнитной теории Максвелла
МГТУ им Н.Э.Баумана
гр. ФН2-41
Котов В.Э.
Вывод и анализ формул Френеля на основе электромагнитной теории Максвелла.
(по материалам лекций Толмачева В.В.)
Постановка задачи
Пусть имеются две диэлектрические среды 1 и 2 , с электрической и магнитной проницаемостью ![]() и
и ![]() соответственно. Из среды 1 в 2 падает плоская монохроматическая волна (границу раздела будем считать плоской).При переходе через границу раздела волна разделится на две части : отраженную волну (в среде 1) и преломленную волну (в среде 2) , необходимо выяснить соотношения между углами
соответственно. Из среды 1 в 2 падает плоская монохроматическая волна (границу раздела будем считать плоской).При переходе через границу раздела волна разделится на две части : отраженную волну (в среде 1) и преломленную волну (в среде 2) , необходимо выяснить соотношения между углами ![]() и
и ![]() , а также между интенсивностями падающей и отраженной волн (рис 1).
, а также между интенсивностями падающей и отраженной волн (рис 1).
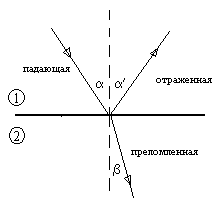
рис.1
Данная волна должна представлять собой точное решение уравнений Максвелла : ![]() и
и ![]() (1) (учитывая , что среда диэлектрическая , т.е.
(1) (учитывая , что среда диэлектрическая , т.е. ![]() )
)
для плоской монохроматической волны точное решение этих уравнений будет (если оси Х направить в сторону распространения волны):
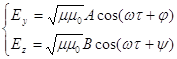 и
и 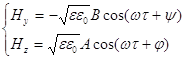 (
(![]() =
=![]() =0) (2)
=0) (2)
где A и B , ![]() и
и ![]() ,
, ![]() - постоянные (не зависят от времени и координаты) ,
- постоянные (не зависят от времени и координаты) ,
![]() и
и![]() - характеристики среды , в которой распространяется волна ,
- характеристики среды , в которой распространяется волна ,
![]() , t - рассматриваемый момент времени
, t - рассматриваемый момент времени
x - рассматриваемая координата на оси Х
V - скорость распространения волны в данной среде
(естественно , в силу линейности уравнений Максвелла любая сумма таких волн будет также их точным решением )
Также она должна удовлетворять условиям на границе раздела : ![]() и
и ![]() не терпят разрыва на поверхности раздела ,
не терпят разрыва на поверхности раздела , ![]() и
и ![]() также не терпят разрыва , поскольку на границе раздела не течет ток и нет поверхностной плотности заряда:
также не терпят разрыва , поскольку на границе раздела не течет ток и нет поверхностной плотности заряда:
![]() (3)
(3)
(индексом 1 обозначаем все , относящееся к первой среде , индексом 2 - ко второй)
Таким образом , необходимо построить точное решение уравнений (1) , удовлетворяющих условиям (3). Для этого рассмотрим два случая : случай ТМ -волны (р-волны ) - вектор ![]() перпендикулярен плоскости падения (трансверсальная магнитная) , и случай ТЕ-волны (s-волны)- вектор
перпендикулярен плоскости падения (трансверсальная магнитная) , и случай ТЕ-волны (s-волны)- вектор ![]() перпендикулярен плоскости падения (трансверсальная электрическая). Любая плоская волна (с любой поляризацией) может быть представлена как линейная комбинация двух таких волн.
перпендикулярен плоскости падения (трансверсальная электрическая). Любая плоская волна (с любой поляризацией) может быть представлена как линейная комбинация двух таких волн.
Случай ТМ -волны (p - волны)
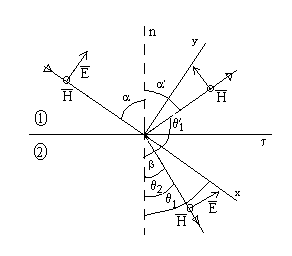
рис.2
Из рисунка видео , что ![]() , запишем условия равенства
, запишем условия равенства ![]() на границе раздела :
на границе раздела :
![]() ( учитывая , что волна в среде 1 есть сумма падающей и отраженной волн)
( учитывая , что волна в среде 1 есть сумма падающей и отраженной волн)
подставляем значения![]() :
:
![]()
подставляем ![]() из (2) :
из (2) :
![]()
Аналогично , поскольку ![]() получаем для вектора
получаем для вектора ![]() на границе раздела:
на границе раздела:
![]() ( c учетом (2) )
( c учетом (2) )
![]()
для выполнения равенств для ![]() и
и ![]() потребуем равенства аргументов косинусов :
потребуем равенства аргументов косинусов :
![]()
потребуем также равенства начальных фаз: ![]()
из рисунка видно , что : ![]()
![]() ,
, ![]() (4)
(4)
(![]() ,
,![]() и
и ![]() - соответственно : угол падения , угол отражения и угол преломления ) , тогда имеем :
- соответственно : угол падения , угол отражения и угол преломления ) , тогда имеем :
![]()
![]()
![]()
из равенства аргументов получаем :
![]()
(т.к. ![]() ,
, ![]() )
)
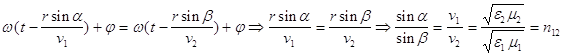 т.е. получены , как и следовало ожидать , законы отражения и преломления света
т.е. получены , как и следовало ожидать , законы отражения и преломления света
разделим теперь выражения для![]() и
и ![]() на
на ![]() , получим (c учетом (4) ) следующую систему :
, получим (c учетом (4) ) следующую систему :
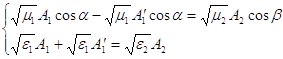 (5)
(5)
здесь неизвестными являются ![]() и
и ![]() , а
, а ![]() - заданно.
- заданно.
Умножим первое уравнение на ![]() а второе на
а второе на ![]() и вычтем из первого второе , тогда члены с
и вычтем из первого второе , тогда члены с![]() сократятся и получим:
сократятся и получим:
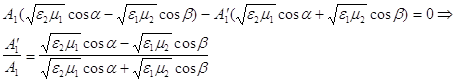
поскольку для неферромагнетиков магнитная проницаемость![]() незначительно отличается от единицы , то для сравнительно широкого класса сред можно считать
незначительно отличается от единицы , то для сравнительно широкого класса сред можно считать ![]() , тогда:
, тогда:
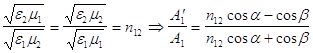 .
.
( разделим числитель и знаменатель на ![]() , и учтя , что
, и учтя , что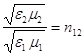 )
)
применив закон преломления , получим (6):
из второго уравнения системы (5) получаем для ![]() :
:
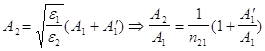 (поскольку полагаем
(поскольку полагаем ![]() ,) , тогда:
,) , тогда:
![]()
![]() (7)
(7)
проверим теперь выполнение еще двух условий на границе раздела ,которые мы не учли -![]() и
и ![]() . Второе равенство выполняется заведомо , поскольку
. Второе равенство выполняется заведомо , поскольку ![]() , проверим первое равенство
, проверим первое равенство ![]() :
:
из рисунка видно , что ![]() , а
, а ![]() подставим значения
подставим значения ![]() ,
,![]() и
и ![]() ( из 2) , сократив сразу на
( из 2) , сократив сразу на ![]() , и учитывая (4) :
, и учитывая (4) :
![]() (выражая
(выражая ![]() через второе уравнение системы (5) )
через второе уравнение системы (5) )
![]()
Таким образом действительно получено точное решение уравнений (2) , удовлетворяющее всем начальным условия. Итак , имеем следующие формулы Френеля для случая s-волны для отражения и преломления (из (6) и (7) ):
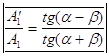 и
и 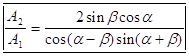
Случай ТЕ -волны ( s - волны)
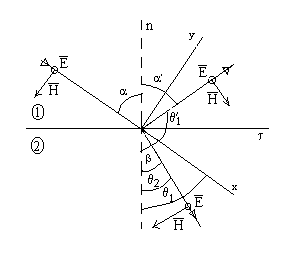
рис.3
Из рисунка видно , что ![]()
Условия (3) для ![]() и
и ![]() :
:
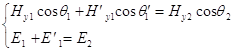
подставляя значения ![]() и
и ![]() из (2) получим :
из (2) получим :
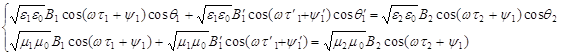 как и в случае ТМ-волны предполагаем равенство аргументов косинусов и совершенно аналогично получаем в этом случае закон отражения и преломления света , сокращая на
как и в случае ТМ-волны предполагаем равенство аргументов косинусов и совершенно аналогично получаем в этом случае закон отражения и преломления света , сокращая на ![]() и с учетом (4) получим систему :
и с учетом (4) получим систему :
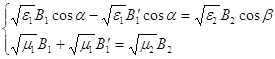 (8)
(8)
умножим первое уравнение на ![]() а второе на
а второе на ![]() и вычтем из первого второе :
и вычтем из первого второе :
![]()
![]()
поскольку мы полагаем ![]() (см. выше) то
(см. выше) то 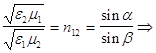
![]() (9)
(9)
из второго уравнения системы (8) получаем:
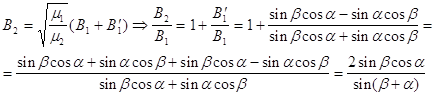 (10)
(10)
проверим теперь неучтенные условия на границе раздела : ![]() и
и ![]() .
.
Второе условие выполняется , поскольку ![]() , проверим выполнение равенства :
, проверим выполнение равенства : ![]() из рисунка видно , что
из рисунка видно , что ![]() , а
, а ![]() подставим значения
подставим значения ![]() ,
,![]() и
и ![]() ( из 2) , сократив сразу на
( из 2) , сократив сразу на ![]() , и учитывая (4) получим :
, и учитывая (4) получим : ![]()
подставляем ![]() из второго уравнения системы (8) :
из второго уравнения системы (8) :
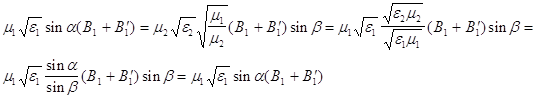
таким образом мы действительно нашли точное решение уравнений (2) , удовлетворяющее всем начальным условиям . В случае p-волны имеем следующие формулы Френеля для отражения и преломления (из (9) и (10))
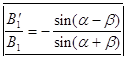 и
и 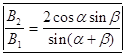
Анализ формул Френеля
Исследуем отношения энергий (точнее плотности потока энергий ) падающей и отраженной ТМ и ТЕ волн и падающей и прошедшей волн в зависимости от угла падения ![]() . Для этого рассмотрим отношение нормальной составляющей вектора Пойтинга
. Для этого рассмотрим отношение нормальной составляющей вектора Пойтинга ![]() падающей и отраженной (
падающей и отраженной (![]() и
и ![]() в случае ТМ и ТЕ волн соответственно) и падающей и прошедшей (
в случае ТМ и ТЕ волн соответственно) и падающей и прошедшей (![]()
и ![]() ) волн. Тогда с из полученных формул Френеля для отражения и преломления , с учетом (2) будем иметь:
) волн. Тогда с из полученных формул Френеля для отражения и преломления , с учетом (2) будем иметь:
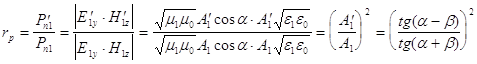
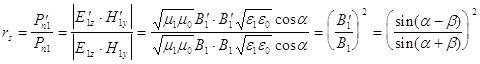
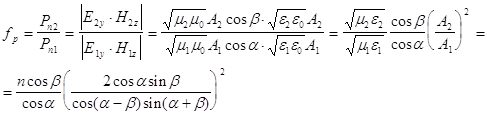
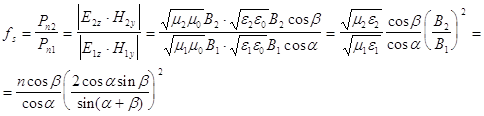
А. Отражение
Исследуем сначала поведение ![]() и
и ![]() на границах отрезка
на границах отрезка ![]() :
:
при ![]() (просто положить
(просто положить ![]() равным нулю нельзя , потому что будет неопределенность ):
равным нулю нельзя , потому что будет неопределенность ):
![]()
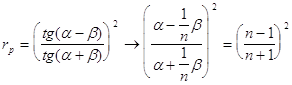
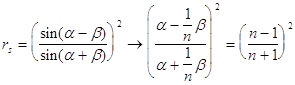
для случая падения из воздуха в стекло (![]() ) :
) : ![]()
т.е. это величина порядка нескольких процентов (можно заметить , что если поменять среды местами - т.е. рассматривать падение из воды в воздух , то это значение не изменится)
В случае падения из оптически менее плотной среды в оптически более плотную при![]() :
:
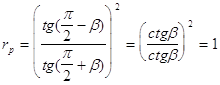
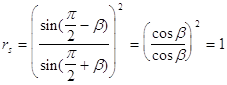
Действительно, преломленной волны при скользящем падении не образуется и интенсивность падающей волны не меняется.
В случае падения из оптически более плотной среды в оптически менее плотную , необходимо учесть явление полного внутреннего отражения , когда прошедшей волны нет - вся волна отражается от поверхности раздела. Это происходит при значениях ![]() больших , чем
больших , чем ![]() , вычисляемого следующим образом:
, вычисляемого следующим образом:
Для падения из стекла в воздух ![]()
Здесь не рассматривается полное внутреннее отражение , поэтому ![]() в случае падения из оптически более плотной среды в оптически менее плотную изменяется до
в случае падения из оптически более плотной среды в оптически менее плотную изменяется до ![]() , в этом случае:
, в этом случае:
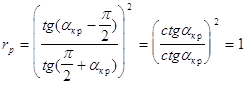
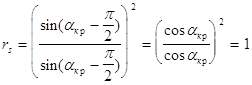
Далее исследуем поведение этих функций между крайними точками , для этого исследуем на монотонность функции: ![]() и
и ![]()
Нам понадобится производная ![]() , найдем ее как производную функции , заданной неявно :
, найдем ее как производную функции , заданной неявно :
![]()
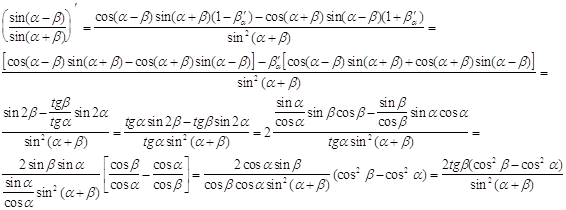 Знак этой производной ( поскольку
Знак этой производной ( поскольку ![]() ,
, ![]() ) зависит только от знака выражения
) зависит только от знака выражения ![]() , это выражение > 0 , когда
, это выражение > 0 , когда ![]() (то есть падение из оптически мене плотной среды в оптически более плотную ) и <0 , когда
(то есть падение из оптически мене плотной среды в оптически более плотную ) и <0 , когда ![]() (из более оптически плотной в менее оптически плотную ) , следовательно в первом случае
(из более оптически плотной в менее оптически плотную ) , следовательно в первом случае ![]() монотонно возрастает, а во втором , убывает . Но в случае
монотонно возрастает, а во втором , убывает . Но в случае ![]()
![]() , следовательно по модулю это выражение будет возрастать , в случае
, следовательно по модулю это выражение будет возрастать , в случае![]()
![]() оно также будет по модулю возрастать . Таким образом ,
оно также будет по модулю возрастать . Таким образом , ![]() , как квадрат этого выражения , в обоих случаях монотонно возрастает от
, как квадрат этого выражения , в обоих случаях монотонно возрастает от ![]() при
при ![]() до 1 при
до 1 при ![]() .или
.или![]() .
.
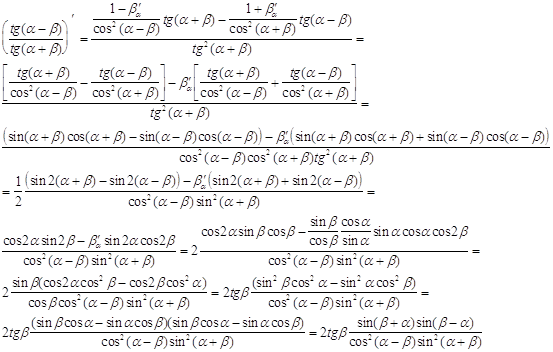
Знак этой производной ,( поскольку ![]() ,
,
есть >0 при ![]() и <0 при
и <0 при ![]() .
.
Знак функции ![]() меняется следующим образом :
меняется следующим образом :
при![]() если
если ![]() невелико
невелико![]() >0 , но эта функция проходит через нуль. Поскольку числитель , при рассматриваемых пределах изменения
>0 , но эта функция проходит через нуль. Поскольку числитель , при рассматриваемых пределах изменения ![]() в 0 обращаться не может(2)(к2) это происходит тогда , когда знаменатель обращается в бесконечность т.е.:
в 0 обращаться не может(2)(к2) это происходит тогда , когда знаменатель обращается в бесконечность т.е.:
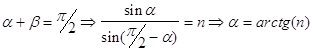
Это есть угол Брюстера (![]() ) , при котором
) , при котором ![]() обращается в 0 , то есть отраженная волна отсутствует . Для случая падения из воздуха в стекло
обращается в 0 , то есть отраженная волна отсутствует . Для случая падения из воздуха в стекло ![]() , для обратного случая (из стекла в воздух)
, для обратного случая (из стекла в воздух) ![]() При переходе через этот угол
При переходе через этот угол ![]() меняет знак на минус , следовательно
меняет знак на минус , следовательно ![]() как квадрат этой функции сначала убывает (до нуля) , а затем возрастает (до 1).
как квадрат этой функции сначала убывает (до нуля) , а затем возрастает (до 1).
При ![]() для небольших
для небольших![]()
![]() <0 , при переходе через
<0 , при переходе через ![]() знак будет меняться на плюс. Переход через
знак будет меняться на плюс. Переход через ![]() действительно будет иметь место , хотя
действительно будет иметь место , хотя ![]() изменяется до
изменяется до ![]() ,а не до
,а не до ![]() , поскольку
, поскольку ![]() . Таким образом
. Таким образом ![]() снова монотонно убывает до 0 , а затем монотонно возрастает до 1.
снова монотонно убывает до 0 , а затем монотонно возрастает до 1.
Итак , в обоих случаях ![]() сначала монотонно убывает от
сначала монотонно убывает от ![]() при
при ![]() до 0 при
до 0 при ![]() , а затем монотонно возрастает до 1 при
, а затем монотонно возрастает до 1 при ![]() или
или ![]() .
.
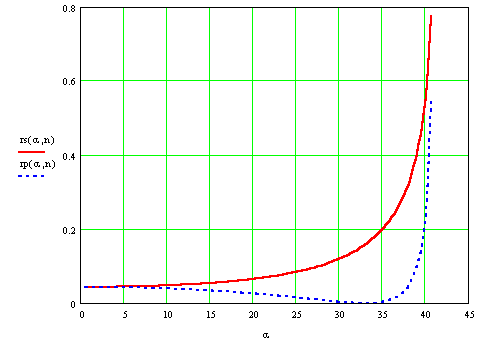
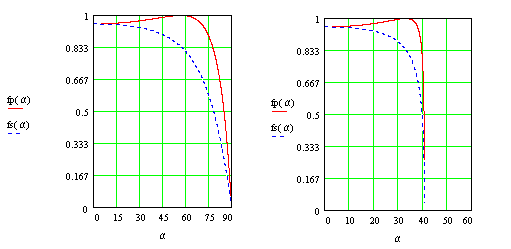
Полученные зависимости иллюстрируются следующими графиками :
на первом показана зависимость ![]() (сплошная линия) и
(сплошная линия) и ![]() (пунктирная линия) от
(пунктирная линия) от ![]() для случая падения волны из воздуха в стекло (n=1.51)
для случая падения волны из воздуха в стекло (n=1.51)
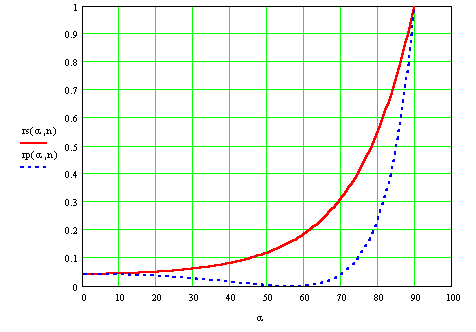
на втором -для случая падения волны из стекла в воздух
В. Преломление
Для анализа поведения ![]() и
и ![]() воспользуемся следующим соображением - падающая волна на границе раздела разделяется на две - прошедшую и отраженную , причем энергия падающей волны (энергия , переносимая волной через границу раздела сред) уходит в энергию отраженной и преломленной волн (поскольку никаких других источников нет). Поэтому , поскольку коэффициент
воспользуемся следующим соображением - падающая волна на границе раздела разделяется на две - прошедшую и отраженную , причем энергия падающей волны (энергия , переносимая волной через границу раздела сред) уходит в энергию отраженной и преломленной волн (поскольку никаких других источников нет). Поэтому , поскольку коэффициент ![]() показывает отношение энергии прошедшей волны к энергии падающей ,
показывает отношение энергии прошедшей волны к энергии падающей , ![]() - отношение энергии отраженной волны к энергии падающей в p-волне , а
- отношение энергии отраженной волны к энергии падающей в p-волне , а ![]() и
и ![]() - аналогичные отношения в s-волне , должны выполнятся соотношения :
- аналогичные отношения в s-волне , должны выполнятся соотношения :
![]() и
и ![]()
Действительно , проверим это :
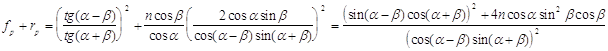
рассмотрим отдельно числитель:
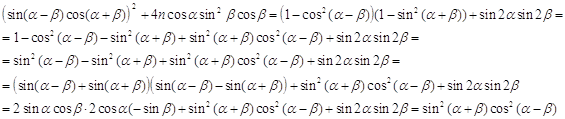 таким образом действительно
таким образом действительно ![]() , аналогично
, аналогично
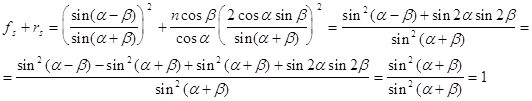
Таким образом , используя предыдущее исследование ![]() ,
,![]() можно сказать , что :
можно сказать , что :
![]()
Для случая падения из воздуха в стекло (а можно заметить , что если среды поменять местами , то это значение не изменится ) ![]()
![]()
Между этими точками ![]() и
и ![]() ведут себя противоположно
ведут себя противоположно ![]() и
и ![]() .
.
Окончательно , ![]() монотонно возрастает от
монотонно возрастает от ![]() (
(![]() )до
)до ![]() , а затем монотонно убывает до 0 ( при
, а затем монотонно убывает до 0 ( при ![]() ) ,
) , ![]() монотонно убывает от
монотонно убывает от ![]() до 0 (при тех же пределах изменения
до 0 (при тех же пределах изменения![]() ). Причем как для случая падения из менее оптически плотной среды , так и из более оптически плотной. Ниже на рисунке представлены графически зависимости для обоих этих случаев.
). Причем как для случая падения из менее оптически плотной среды , так и из более оптически плотной. Ниже на рисунке представлены графически зависимости для обоих этих случаев.
С. Набег фаз при отражении и преломлении
Из формул Френеля следует , что отношения ![]() ,
,![]() ,
,![]() и
и ![]() могут в принципе получится и отрицательными . Поскольку амплитуда есть существенно положительная величина , в этом случае имеет место сдвиг фазы волны на
могут в принципе получится и отрицательными . Поскольку амплитуда есть существенно положительная величина , в этом случае имеет место сдвиг фазы волны на![]() . Далее выясним , когда такой сдвиг имеет место.
. Далее выясним , когда такой сдвиг имеет место.
В случае отраженной p-волны ![]() , как установлено в п. А , эта функция
, как установлено в п. А , эта функция
при n>1 больше 0 при ![]() и меньше 0 при
и меньше 0 при ![]() , при n<0 промежутки знакопостоянства меняются местами . Таким образом , в случае падения из менее оптически плотной среды в более плотную сдвиг фаз на
, при n<0 промежутки знакопостоянства меняются местами . Таким образом , в случае падения из менее оптически плотной среды в более плотную сдвиг фаз на![]() в отраженной p-волне наблюдается при
в отраженной p-волне наблюдается при ![]() , а в случае падения из более плотной в менее плотную - при
, а в случае падения из более плотной в менее плотную - при![]() .
.
В случае отраженной s-волны ![]() , эта функция меньше 0 при
, эта функция меньше 0 при ![]() и больше 0 в противном случае. Таким образом , сдвиг фаз на
и больше 0 в противном случае. Таким образом , сдвиг фаз на![]() в отраженной s-волне наблюдается при падении из менее оптически плотной среды в более плотную , и не наблюдается при падении из более плотной среды в менее плотную.
в отраженной s-волне наблюдается при падении из менее оптически плотной среды в более плотную , и не наблюдается при падении из более плотной среды в менее плотную.
В случае произвольно падающей линейно поляризованной волны , которая представляется в виде суммы p и s-волн , в отраженной волне , таким образом , можно получить , в общем случае волну произвольной (эллиптической) поляризации .
Для исследования сдвига фаз в прошедшей волне , воспользуемся соотношениями , возникшими как промежуточные результаты при выводе (7) и (10) :
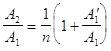 и
и ![]()
из этих соотношений видно , что , поскольку 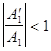 и
и 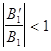 , то всегда
, то всегда ![]() и
и ![]() . То есть , в прошедшей волне изменения фазы не происходит (причем это верно для волн произвольной поляризации).
. То есть , в прошедшей волне изменения фазы не происходит (причем это верно для волн произвольной поляризации).
Дополнительная литература:
Cивухин Д.В. “Общий курс физики. Оптика” , Москва , “Наука”,1985г.
Савельев И.В. “Курс общей физики” , том 2 , Москва , “Наука” , 1979г.