Матанализ
1Натуральные числа – 1,2,3,4, …., счёт предметов, указание порядкового номера. Натуральные числа также называют положительными целыми числами. Числа –1,-2, -3, …, противоположные натуральным называются отрицательными целыми числами. Число 0 тоже целое. Рациональные числа – целые и дроби (+,-) Вид М/N, где (N![]() 0) M и N- взаимно простые целые числа. Иррациональные - √2 все вышепереч-е + бесконечные непериодич. дроби. Все эти числа – действительные. Компл. число Z1=A1+iB1; iІ=-1
0) M и N- взаимно простые целые числа. Иррациональные - √2 все вышепереч-е + бесконечные непериодич. дроби. Все эти числа – действительные. Компл. число Z1=A1+iB1; iІ=-1
2 Z1±Z2=(A1±A2)+i(B1±B2)
Z1*Z2=(A1+iB1)*(A2+iB2)
Z1/Z2=(a1+ib1)(a2-ib2)/(a2+ib2)(a2-ib2)=(a1a2+b1b2)+
i(b1a2-a1b2)\a2І+b2І=(a1a2+b1b2/a2І+b2І)+i* (b1a2-
a1b2/a2І+b2І)
3 Тигонометрическая форма комплексного числа
Z=a+ib=r*cosφ+i*r*sinφ=r*(cosφ+i*sinφ)
r – модуль; φ – аргумент. b – y; a – x.
4 ZЄ=rЄ(cos Aφ+i*sin Aφ)
5 Є√Z=Є√r(cos φ+2πk/а +i *sin φ+2πk/a) k∈(1;2;3…a-1)
Все корни А-ой степени лежат на окружности r=| Z |№\а и являются вершинами правильного А-угольника, вписанного в эту окружность.
6 Переменная вел. Х, принимающая последовательно ( с возрастанием номера n ) значения х1,х2,х3..хN называется числовой последовательностью
1,1,1,1,1…1
1,1/2,1/3…1/N
1,-1,1,-1…(-1)Є
Xn,n∈N
Число А наз. пределом последовательности Хn если для любого сколь угодно малого положит. числа E>0 найдётся такой номер N(E), что как только n>N(E) то имеет место неравенство | Xn – A | < E
lim Xn = A
n→∞
Число А есть предел последовательности Xn если для любого ε > 0 найдётся такой номер N, начиная с которого (при n>N) все члены последовательности будут заключены в ε-окрестности какой бы она узкой ни была. Вне этой окрестности может быть лишь конечное число членов этой последовательности.
7 Если последовательность Хn монотонна и ограничена, то она имеет предел (сходится).
Cвойства пределов:
если Хn=С то lim Xn=C
n→∞
пусть lim Xn=A, a lim Yn=B тогда lim (Xn±Yn)=A±B
n→∞ n→∞ lim (Xn*Yn)=A*B
lim (Xn/Yn)=A/B ; B≠0
если Xn≤Yn для n∈N то lim Xn ≤ lim Yn
n→∞ n→∞
8 Eсли Хn сходится (имеет предел) то Хn ограничена
Последовательность Xn; n∈N наз. ограниченной если существует положительное число М, что выполняется нер-во | Xn |≤M; n∈N
Если lim Xn=0, то Xn; n∈N наз. БМВ обознач (αn,βn,γn)
n→∞
Св-ва БМВ:
lim αn=0
n→∞
lim (αn±βn)=0
n→∞
lim (Xn*αn)=0; если Xn-ограничена
n→∞
В произведении БМВ можно заменять на эквивалентную БМ. В алгебраической сумме замену можно производить в том случае если не происходит сокращения БМ одного порядка с Х:
sin X ~ X eЄ-1 ~ a
tg X ~ X (1+x)Є ~ ax
1 – cos X ~ XІ/2 arctg X ~ X
LOGe(1+X) ~ X xЄ-1 ~ aLNx
9 Сумма эл-тов числовой последовательности наз. числовым рядом.
![]()
Сумма n членов ряда – n частичная сумма ряда
Если при n→∞ lim Sn=S, то ряд сходящийся, S сумма ряда .
Ряд наз. сходящимся если сущ. конечный предел последовательности его частичных сумм.
Прим:
![]() при каких q сходится и расходится ?
при каких q сходится и расходится ?
сходится к сумме S=a/1-q при | q |<1 и расход-ся при | q |≥1
10 Признак сравнения двух знакоположит-х рядов.
есть 2 знакполож. ряда ∑Ak,∑Bk так что 0≤Ak≤Bk k∈N
тогда если ∑Bk⇒ то ∑Ak тоже ⇒ и наооборот если меньший ряд не сходится то и больший тоже.
11 Признак Даламбера
∑Un c положительными членами сущ. lim Un+1/Un =l
n→∞
то ряд сходится если l<1 и расходится если l>1, если l=1 то вопрос о сходимости нерешён.
Признак Коши
∑An – знакополож. ряд lim Є√An=q
n→∞
q<1 – сходится ; q>1 – расходится.
12 Знакопеременный ряд а1-а2+а3-а4…+ (-1)в степ.(n-1)*An
An>0
Признак Лейбница:
Если члены ряда (знакопер) убывают а1>a2>a3>…An и
предел Аn при n→∞ =0 то ряд сходится
пример 1-1/2+1/3-1/4…+(-1)(n-1)*1/n
13 Имеет место функциональная зависимость между двумя переменными величинами х и у если задан закон y=f(x), согласно которому каждому х∈Х соответствует значение y∈Y. х-аргумент
y=kx+b – линейная ф-ия
y=axІ+bx+c – квадратичная ф-ия
Обратная ф-ия – ф-ия x=φ(y) наз. обратной ф-ией к прямой ф-ии y=f(x) если x=φ(f(x)) для всех х∈Х
Графики взаимно обратных ф-ий симметричны относительно прямой у=х.
y=XЄ и y=LOGxA – примеры
14 Число B называется пределом ф-ии в f(x) при x, стремящемуся к x0 (или в точке x0) если для любого, сколь угодно малого положительного числа ε>0, найдётся такое положительное число δ(ε)>0 что для всех х не равных х0 и удовлетворяющих условию | x-x0 |<δ выполняется нерав-во | f(x)-B | < ε
lim f(x)=B
x→x0
Смысл состоит в том, что для всех значений х, достаточно близких к х0, значения ф-ии f(x) как угодно мало отличаются от числа В (по модулю)
15 lim f(x)=B
x→x0
Если B=f(x0), то ф-ия f(x) – непрерывна в точке х0.
св-ва :
lim c=c
x→x0
если f(x)=b, φ(x)=c то lim (f(x)±φ(x))=b±c
x→x0
lim (f(x)*φ(x))=b*c
x→x0
lim (f(x)/φ(x))=b/c (c≠0)
x→x0
Если f(x)≤φ(x)≤g(x) и lim f(x)=lim g(x) =b то lim φ(x)=b
x→x0 x→x0 x→x0
если при этом b=f(x0); c=φ(x0) то св-во 2 можно записать:
(Если f(x) или φ(х) непрерывны в т. х0 то в т.х0
непрерывны сумма, разность, произведение и
частное(φ(х0))≠0 этих функций
Если ф-ия непрерывна в каждой точке отрезка, то она непрерывна на этом отрезке
16 Линейная ф-ия непрерывна в любой точке А∈(-∞;+∞)
y=kx+b=f(x)
f(A)=kA+b
k≠0 ⇒ | f(x)-f(a) |<ε | kx-b-ka+b | <ε
| k (x-f) | <ε
| k |*| x-a | <ε
| x-a | < ε/| k |=δ(ε)
y=axІ+bx+c (-∞;+∞)
17 y=BЄ (B>0)
Докажем, что y=BЄ непрерывна на (-∞;+∞)
lim BЄ=1
a→0
| BЄ-1 | <ε 1) B=1
2) B>1
-ε < BЄ-1 < ε 1-ε < BЄ < ε+1
LOGb(1-ε) min {-LOGa(1-ε); LOGa(1+ε)}= δε | x | < δε LOGaB 18 y=cos x (-∞; +∞) | cos x – cos a | < ε | 2 sin (x-a)/2 + sin (x+a)/2 | < ε 2 | sin (x-a)/2 | + | sin (x+a)/2 | < ε 2 | sin (x-a)/2 | < ε | x-a | < ε =δ(ε) y=sin x (-∞; +∞) y=tg x=sin x/cos x кроме x=π/2+πk y=ctg x=cos x/sin x кроме x=πk 19 Первым замечательным пределом называется lim sin x/x=1 x→x0 20 Второй замечательный предел lim(1+1/a)Є=e a→∞ Число е (число Эйлера, неперово число) играет важную роль в матанализе. lim (1+a)№’Є=e a→0 21 Пусть имеется ф-ия y=f(x), определённая на (а; в), говорят что ф-ия имеет в т. х0∈(а; в) производную f ’(x0) если существует предел lim (f(x)-f(x0))/(x-x0) x→x0 Производной ф-ии y=f(x) в точке х0 называется предел отношения приращения ф-ии к приращению аргумента, когда приращение аргумента стремится к нулю. Ф-ия имеющая производную в каждой точке интервала называется дифференцируемой на этом интервале. Геометрический смысл производной: пр-ая f `(x0) есть угловой коэфф. (tg угла наклона) касательной, проведённой к кривой y=f(x) в точке х0 , k=f ‘(x0) у=f ‘(x0)(x - x0) Механический смысл производной: пр-ая пути по времени s ‘(t0) есть скорость точки в момент t0: V(t0)=s ‘(t0) Определение для любой точки 22 Производная алгебраической суммы конечного числа дифференцируемых ф-ий равна такой же сумме производных этих ф-ий (u±v)`=u`± v` Производная произведения двух дифференцируемых ф-ий равна произведению пр-ой первого сомножителя на второй плюс произведение первого сомножителя на про-ую второго: (uv)`=u`v + uv` Постоянный множитель можно выносить за знак производной (cu)`=cu` Производная произведения нескольких дифференцируемых ф-ий равна сумме произведений производной каждого из сомножителей на все остальные (uvw)`=u`vw+uv`w+uvw` 23 Производная частного двух ф-ий u(x)/v(x), если v(x)≠0 равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя есть квадрат прежнего знаменателя: (u/v)`=(u`v-uv`)/vІ; v≠0 (u/c)`=1/c*u` (c/u)`=-cv`/vІ c=const 24 (xЄ)`=axЄˉ№ 25 (LNx)`=1/x (eЄ)`=eЄ Для дифференцируемой ф-ии с производной, не равной 0, производная обратной ф-ии равна обратной величине производной данной ф-ии X`y = 1/Y`x 26 (sin x)`=cos x (cos x)`=-sin x (tg x)`=1/cosІx (ctg x)`=-1/sinІx 27 Если y=f(u) и u=φ(x) – дифференцируемые ф-ии от своих аргументов, то производная сложной ф-ии существует и равна производной данной ф-ии по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по незавмсимой переменной х y`=f`(u)*u` y=f(u(x)) Fx`=Fu`*Ux` Пример: y=(√x+5)і y`=? y=uі, где u=√x+5 по формуле : y`=3u`*u`=3(√x+5)І(√x+5)`=3(√x+5)І/2√x 28 Дифференциалом ф-ии наз. линейная часть приращения ф-ии (относительно Δх), равная произведению производной на приращение независимой переменной. dy=f`(x)Δx Дифференциал независимой переменной равен приращению этой переменной. Геометрический смысл: Дифференциал ф-ии есть приращение ординаты касательной, проведённой к графику ф-ии y=f(x) в данной точке когда х получает приращение Δх 29 При исследовании ф-ий используется следующий алгоритм: 1 ООФ, ОЗФ 2 Непрерывность ф-ии 3 Нахождение асимптот 4 Экстремумы и интервалы монотонности 5 Интервалы выпуклости и т. перегиба 6 Чётность нечётность, периодичность 7 Т. пересечения с Ох и Оу (3)Если для некоторого х0 имеет место предел f(x)=∞ при х→х0 то говорят, что х=х0 явл. вертикальн. асимптотой f(x) Если предел f(x)=b при x→∞ то говорят, что у=b явл. горизонтальной асимптотой f(x) Если предел f(x)/х=k при x→∞ (k≠0;k≠∞) и предел (f(x)-kx)=b, то y=kx+b является наклонной асимпт-й (4)Если производная ф-ии положительна (отрицательна) внутри некоторого промежутка Х то ф-ия возрастает (убывает) на этом промежутке Если при переходе через т. х0 производная дифференцируемой ф-ии меняет свой знак и в т. х0 равна 0 то х0-точка экстремума (минимума или максимума) (5)Точкой перегиба непрерывной ф-ии (f``(x)=0) наз. т. в разделяющая интервалы, в которых ф-ия выпукла вниз и вверх. Ф-ия y=f(x) называется выпуклой внизу на интервале (a;b) если f``(x)>0 на (a;b); ф-ия называется выпуклой вверх на (a;b) если f``(x)<0 на (a;b) 30 Асимптотой графика ф-ии y=f(x) называется прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к 0 при неограниченном удалении точки графика от начала координат. Если для некоторого х0 имеет место предел f(x)=∞ при х→х0 то говорят, что х=х0 явл. вертикальн. асимптотой f(x). Вертикальные асимптоты следует искать в точках разрыва ф-ии или на концах её ООФ (а; в) если аи в – конечные числа Если предел f(x)=b при x→∞ то говорят, что у=b явл. горизонтальной асимптотой f(x) Если предел f(x)/х=k при x→∞ (k≠0;k≠∞) и предел (f(x)-kx)=b, то y=kx+b является наклонной асимпт-й Наклонная асимптота как и горизонтальная может быть правосторонней или левосторонней 31 Степенным рядом наз. ряд вида (1)∑ Bn*xЄ = b0+b1x+b2xІ…+baxЄ+… это ряд в котором членами являются ф-ии, в частности степенные. Совокупность тех значений х, при которых степнной ряд сходится, называется областью сходимости степнного ряда. Ряд (1) наз. абсолютно сходящимся рядом, если сходится ряд (2) ∑ | bn |*| x |Є Т1. Если ряд (2) сходится, то сходится и ряд (1) Т2. Для любого степ. ряда (1) сущ-ет такое неотрицат. число R≥0 что этот ряд сходится абсолютно при | x | Даламбер: lim | Bn+1 |/| Bn |<1 (n→∞) сходится >1 (n→∞) расходится 32 Разложение ф-ий в ряд: Если бесконечно дифференцируемая ф-ия f(x0)=a0 f`=A1+2A2(x-x0)+n*An(x-x0)Єˉ№ f(x)=f(x0)+f1(x0)(x-x0)+…+fЄ(x0)(x-x0)Є/a! Рядом Тейлора ф-ии f(x) в окрестности т. х0 называется степ. рядом отн. разности (х-х0) Особенно часто используется разложение ф-ии в ряд по степеням х, при этом х0=0; f(x)=f(0)+f`(0)+f Є(0)/a!*xЄ Ряд Маклорена – частный случай ряда Тейлора eЄ=1+x+xІ/2!+xі/3!+…+xЄ/a!+… sin x=1+ x-xі/3+…+(-1)Є*(xІЄˉ№)/(2a+1)!+… cos x=1-xІ/2!+x⁴/4!+…+(-1)ⁿ*xІⁿ/(2n)!+… ln(1+x)=x-xІ/2+xі/3-…+(-1)ⁿxⁿ⁺№/n+1… 33 Ф-ия F(x) наз. первообразной для ф-ии f(x) если для всех х (из области определения) имеет место F`(x)≡f(x) нетрудно увидеть что если F(x) является первообразной для f(x) то и для F(x)+C также явл. первообразной. Общий вид первообразной F(x)+C называется неопределённым интегралом от ф-ии f(x) обозначается F(x)+C=∫f(x)dx dF(x)=F`(x)dx=f(x)dx Св-ва неопр.∫ ∫dF(x)=F(x)+C (∫f(x)dx)`=f(x) ∫αf(x)dx=α∫f(x)dx ∫(f(x)±g(x))dx=∫f(x)dx±∫g(x)dx Таблица интегралов 34 Метод замены переменных: ∫f(x)dx=∫f(φ(t))·φ`(t)dt → x=φ(t) ∫sin 5x dx=∫sin t 1/5dt=1/5∫sin t dt=-1/5 cost+C =-1/5cos 5x+C 5x=t; x=1/5t; dx=1/5 dt 35 Интегрир-ие по частям: ∫ U·dV=UV-∫VdU Возможности применения связаны с тем, что дифференцир-ие может существенно упростить один из сомножителей (при условии что дифф-ие не слишком усложнит другой) ∫ xІ=U dU=2x dx sin x dx =dV V=-cos x ∫ x=U dU=dx cos x dx=dV V=sin x ∫ = xІ·sin x dx=-xІcos x +2(x·sin x-∫sin x dx)= -xІ·cos x+2x·sin x +2cos x+C 36 Рациональной дробью называется ф-ия, равная отношению двух многочленов f(x)=Pm(x)/Qn(x), Pm(x)-многочлен степени m, Qn(x)- многочлен степени n. Рациональная дробь наз. правильной если степень числителя меньше степени знаменателя, т.е. m Интегрирование дробей методом разложения на элементарные дроби: 1 Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби. 2 Разложив знаменатель дроби на множители, представить её в виде суммы простейших рац. дробей. 3 Проинтегрировать многочлен и полученную сумму простейших дробей. 37 Определённым интегралом от ф-ии f(x) на отрезке (a; b) называется предел интегральной суммы Sn, когда n→∞ (Δxi→0) Cв-ва опр. интеграла: (все интегралы на отрезке от А до В) 1 ∫С·f(x)dx=C·∫f(x)dx 2 ∫(f(x)±g(x))dx=∫f(x)dx±∫g(x)dx 3 ∫f(x)dx=-∫f(x)dx 4 Если f(x)≤g(x) на (A,B), то ∫f(x)dx≤∫g(x)dx 5 Если на (А,В) m=minf(x) M=maxf(x)то m(B- -A)≤∫f(x)dx≤M(B-A) 6 Если f(x) непрерывна на (A,B) то сущ. также точка С∈(A;B) ∫f(x)dx=f(C)·(B-A) 7 Если f(x) непрерывна на (А,В) то ∫f(x)dx существует 8 ∫f(x)dx=∫(a→d)f(x)dx+∫(d→b)f(x)dx 9 Формула Ньютона-Лейбница: ∫f(x)dx=F(B)-F(A)→F`(x)=f(x) 38 Применение опр. ∫ 1 Вычисление площадей (Н-Лейб) Если на (А,В) f(x)>0 то S=∫f(x)dx Если на (А,В) f(x)<0 то S=-∫f(x)dx Если на (А,В) f(x)>g(x) то S=∫(f(x)-g(x))dx (действительно для всех вариантов расп. ф-ий) 2 Вычисление объёмов тел вращения V=π∫fІ(x)dx 39 Приближ. вычисление интегралов 1 Формула Н-Лейб. 2 Метод прямоугольника (B-A)/n=h: ∫(A→B)f(x)dx~=h(f1+f2…+fn) 3 Формула трапеции ∫f(x)dx~=h(1/2·f0+f1+f2+…fn) 4 Формула Симпсона n-чётное ∫f(x(dx=(B-A)/3n(f0+4f1+2f2+4f3+2f4+…+4fn-1+fn) 40 Несобственные ∫ бывают 2-х видов: ∫-ы вида ∫(a;+∞)f(x)dx; ∫(-∞;b)f(x)dx; ∫(-∞;+∞)f(x)dx называются несобственными ∫-и 1-го рода Если сущ. предел (b→∞) ∫(a;b)f(x)dx=C (C≠∞) то интеграл сходится и наоборот. Пусть есть числовой ряд ∑Ax=A0+A1+…An+… и пусть есть ф-ия f(x)=Ax на интервале ( a:b) Тогда ряд и несобственный ∫(a;∞)f(x)dx сходятся или расходятся одновременно Если lim (x→b)f(x)=∞ или lim(x→a)f(x)=∞ то ∫f(x)dx наз. несобственным интегралом 2-го рода, он сходится если сущ. конечный предел lim ∫(a; b-δ)f(x)dx δ→0 41 Пусть имеется n переменных величин, и каждому набору их значений (x1,x2,x3…xn) из некоторого мн-ва Х соответствует одно вполне определённое значение переменной величины Z. Тогда говорят,что задана ф-ия нескольких переменных Z=f(x1…xn) Если сущ-ет lim(Δx→0)f(x+Δx,y)-f(x,y)/Δx=fx`(x,y) то он называется частной производной по переменной х. Если сущ-ет lim(Δy→0)f(x,y+Δy)-f(x,y)/Δy=fy`(x,y) то он называется частной производной по переменной y Величина dZ=f`x(x;y)dx+f`y(x;y)dy называется дифференциалом от ф-ии f(x;y) Z=f(x1+x2+…xn)dZ=f`x1·dx1+f`x2·dx2+…+f`xn·dxn Дифференциалом ф-ии называется сумма произведений частных производных на приращение соответствующих независимых переменных. 42 Если Z=f(x;y) имеет в точке (х0;у0) экстремум (локальный) и ф-ия дифференцируема (т.е. имеет частные произв-ые) то частные произв-ые в этой т. равны 0. 43 Формулы служащие для аналитического представления опытных данных получили название эмпирических формул Этапы вывода ЭФ: 1 Установить вид зависимости (линейная, квадратичная, логарифмическая и т.д.) 2 Определение известных параметров этой ф-ии Для линейной зависимости сущ-ет метод наименьших квадратов 44 ДУ называют ур-ие, связывающее искомую ф-ию одной или нескольких переменных, эти переменные, и производные различных порядков данной ф-ии. Решением ДУ называется такая ф-ия, котю при подстановке её в это ур-ие обращает его в тождество. ДУ первого порядка наз. ур-ие содержащее переменную х, неизвестную ф-ию y=f(x) и её производную y`=f`(x) ДУ первого порядка наз. ур-ем с разделяющимися переменными, если оно м/б представленно в виде dy/dx=f(x)g(y) Для решения такого ур-ия его следует преобразовать к виду, в котором дифференциал и ф-ии переменной х окажутся в одной части равенства, а переменной у – в другой. Затем проинтегрировать обе части полученного рав-ва: dy/g(y)=f(x)·dx → ∫ dy/g(y)=∫ f(x)·dx axЄˉ№ -1/√1-xІ |x|<1 1/√(1+xІ) xЄ⁺№/a+1+C a≠1 1/a·arctg x/a+C a≠0 1/2a·ln| (a+x)/(a-x) |+C a≠0 Понятие числа (от натур. до комплексного) Сложение, вычитание, *, / для комплексного числа Тригонометрическая форма комплексного числа Возведение в степень комплексного числа Извлечение Є из комплексного числа Последовательность и её предел Св-во сходящихся последовательностей (док-во) БМВ и ограниченная последовательность. Св-ва БМВ Знакоположительный ряд и его сходимость (пример) Признак сравнения двух знакоположительных рядов (примеры) Признаки Даламбера и Коши Знакопеременный ряд. Признак Лейбница (пример) Прямая и обратная функция (примеры) Предел ф-ии в точке Непрерывность ф-ии в точке. Св-ва непрерывных ф-ий Непрерывность линейной и степенной ф-ий Непрерывность ф-ий ВЄ и LOGaX Непрерывность тригонометрической ф-ии 1-ый замечательный предел 2-ой замечательный предел и его применение для начисления непрерывных % Понятие производной от ф-ии. Геометрический и механический смысл призводной Понятие пр-ой. Пр-ая от +, -, * двух ф-ий Понятие пр-ой. Пр-ая от / двух ф-ий Понятие пр-ой. Пр-ая от ХЄ Понятие пр-ой. Пр-ая от обратных ф-ий (LNx, eЄ) Пр-ая от тригонометрической ф-ии. Пр-ая от сложной ф-ии (пример) Понятие дифференциала ф-ии. Его геометр. смысл Исследование ф-ий с помощью пр-ой и пределов. Понятие асимптот и их нахождение Степенной ряд и область его сходимости Разложение ф-ий в степенные ряды Неопределённый интеграл. Табл. Интегралов Метод интегрир-ия с помощью замены переменных (примеры) Интегрирование по частям Интегрир-ие с помощью разложения на элементарнве дроби Определённый интеграл и его св-ва. Формула Ньютона-Лейбница Применение опр. интегралов Приближённый метод вычисления опр. интегралов Несобственные интегралы Ф-ии нескольких переменных. Понятие частных пр-ых и дифференциала Экстремум ф-ий нескольких переменных Понятие об эмпирических формулах. Метод наименьших квадратов. 44 Понятие ДУ и методы его решения.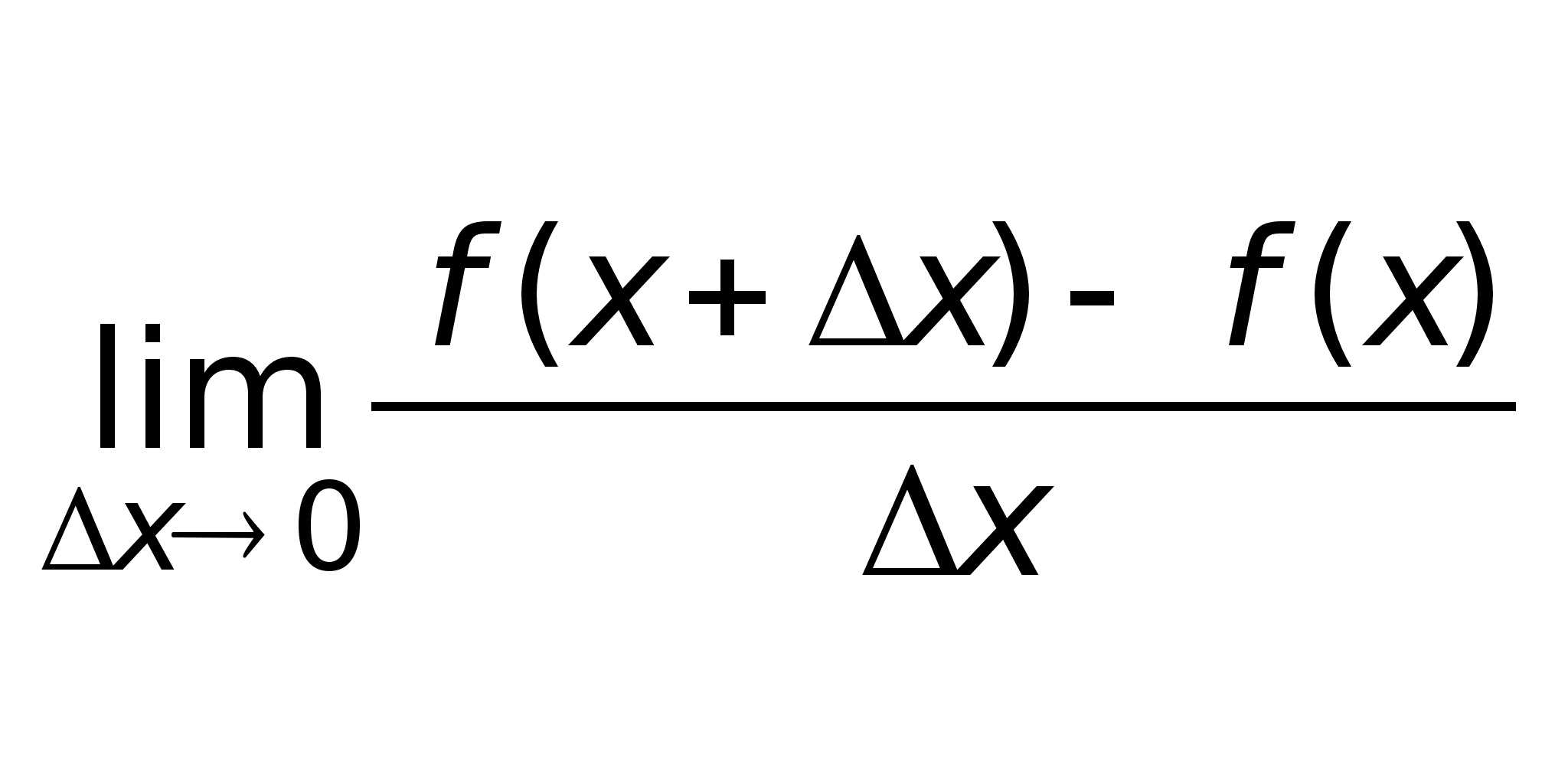
![]() xІ·sinx dx
xІ·sinx dx![]() = xІ·sin x dx=-xІ·cos x -∫(-cos x)2x dx=-xІ·cos x+2∫x·cos x dx
= xІ·sin x dx=-xІ·cos x -∫(-cos x)2x dx=-xІ·cos x+2∫x·cos x dx![]()
f(x) f`(x) f(x) f`(x) c 0 xЄ x 1 xІ 2x √x 2√x arccos x 1/x -1/xІ arctg x 1/1+xІ eⁿ eⁿ arcctg x -1/1+xІ aⁿ aⁿln a sh x ch x ln x 1/x ch x sh x LOGaX 1/x·ln a th x 1/chІx sin x cos x cth x -1/shІx cos x -sinx ln(x+√(xІ+1)) tg x 1/cosІx arcsin x 1/√(1-xІ) ctg x -1/sinІx f(x) F(x)+C 0 C 1 x+C x xІ/2+C xЄ 1/x ln| x |+C 1/xІ -1/x+C 1/xі 1/2xІ+C 1/(1+xІ) arctg x+C 1/aІ+xІ 1/1-xІ 1/2·ln| (1+x)/(1-x) |+C 1/aІ-xІ x/xІ+a 1/2·ln| xІ+a |+C 1/√(1-xІ) arcsin x+C 1/√(aІ-xІ) arcsin x/a+C eⁿ eⁿ aⁿ aⁿ/ln a ln x x ln x –x +C sin x -cos x+C cos x sin x+C tg x -ln | cos x |+C ctg x ln | sin x |+C 1/cosІx tg x+C 1/sinІx -ctg x+C